- 2021-05-22 发布 |
- 37.5 KB |
- 22页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【物理】2019届二轮复习传送带模型学案(全国通用)
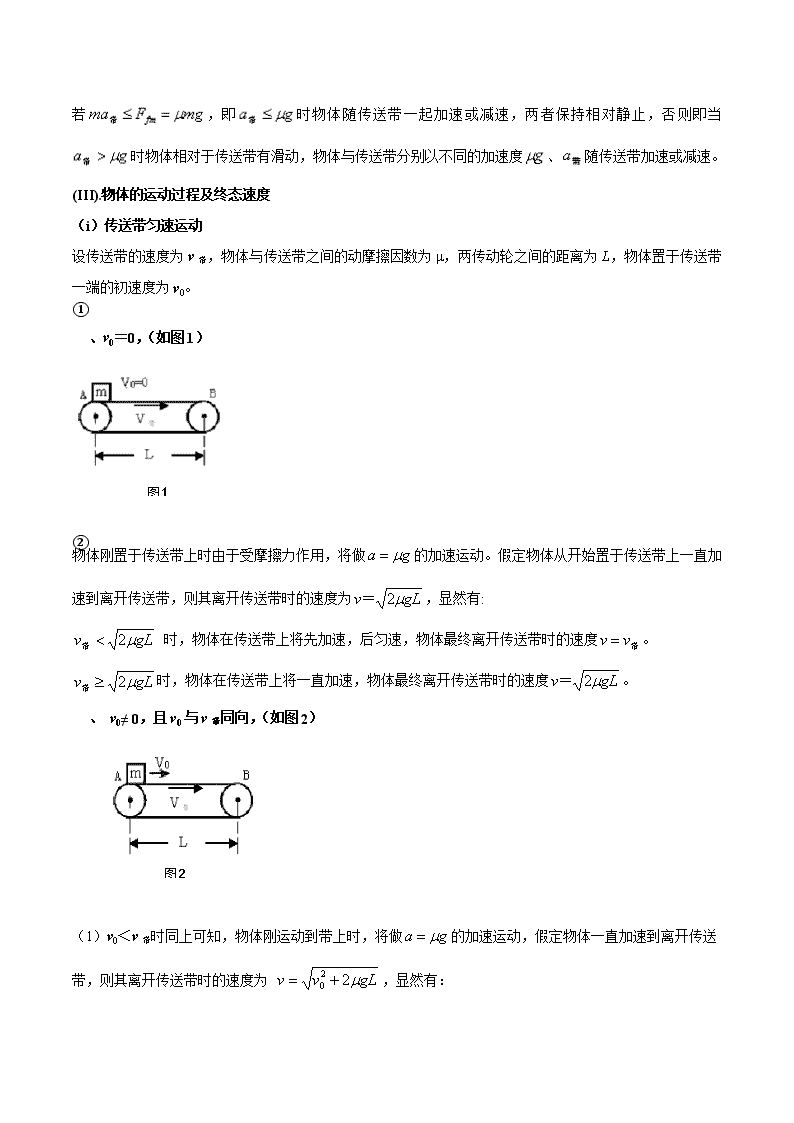
高中物理系列模型之实物模型 7.传送带模型(1) 模型界定 本模型是指传送带水平放置的情形,主要涉及物体在传送带上发生相对滑动的过程中位移、时间等运动学问题及动能、热量等能量问题。 模型破解 1.水平传送带 (I)物体所受外力 (i)通常除重力、支持力外只有摩擦力 当传送带匀速运动,物体与传送带间有相对运动时物体受到摩擦力的作用,无相对运动时则无摩擦力的作用。 (ii)当传送带做变速运动时,无论物体与传送带之间是否有相对运动,物体都要受到摩擦力的作用。 (iii)当传送带做变速运动时,物体能与传送带保持相对静止的必要条件是,其中是物体与传送带之间的动摩擦因数。 (II).物体的运动性质 (i)若传送带匀速运动: ①当物体与传送带的运动方向相反时,物体一定受到与传送带运动方向相同的滑动摩擦力的作用而减速运动; ②当物体与传送带运动方向相同时,若,物体受到与运动方向相同的摩擦力而加速,若,物体受到与运动方向相反的摩擦力而减速,在时物体随传送带一起匀速运动。 (ii)若传送带做变速运动: ①当物体与传送带的运动方向相反时,无论传送带运动的加速度情况如何,物体一定做加速度为的匀减速运动,直到速度减小到零为止; ②当物体与传送带的运动方向相同时,仍有时物体受到与运动方向相同的摩擦力而加速,时物体受到与运动方向相反的摩擦力而减速,这与传送带运动的加速度大小、方向无关,但当时,物体仍受到摩擦力的作用,其方向与传送带的加速度方向一致,此后物体能否随传送带一起做变速运动需要分情况讨论: 若,即时物体随传送带一起加速或减速,两者保持相对静止,否则即当时物体相对于传送带有滑动,物体与传送带分别以不同的加速度、随传送带加速或减速。 (III).物体的运动过程及终态速度 (i)传送带匀速运动 设传送带的速度为v带,物体与传送带之间的动摩擦因数为μ,两传动轮之间的距离为L,物体置于传送带一端的初速度为v0。 ①、v0=0,(如图1) 图1 物体刚置于传送带上时由于受摩擦力作用,将做的加速运动。假定物体从开始置于传送带上一直加速到离开传送带,则其离开传送带时的速度为,显然有: 时,物体在传送带上将先加速,后匀速,物体最终离开传送带时的速度。 时,物体在传送带上将一直加速,物体最终离开传送带时的速度。 ②、 v0≠ 0,且v0与v带同向,(如图2) 图2 (1)v0<v带时同上可知,物体刚运动到带上时,将做的加速运动,假定物体一直加速到离开传送带,则其离开传送带时的速度为 ,显然有: 时,物体在传送带上将先加速后匀速,物体最终离开传送带时的速度。 时,物体在传送带上将一直加速,物体最终离开传送带时的速度。 (2)v0>v带时 因v0>v带,物体刚运动到传送带时,将做加速度大小为的减速运动,假定物体一直减速到离开传送带,则其离开传送带时的速度为 ,显然: 时,物体在传送带上将一直减速,物体最终离开传送带时的速度。 时,物体在传送带上将先减速后匀速,物体最终离开传送带时的速度。 (3)v0=v带时 因v0=v带,物体与传送带之间无相对运动,物体不受到摩擦力的作用,物体一直随传送带匀速运动,最终离开传送带时的速度v=v0=v带。 ③、 v0≠ 0,且v0与v带反向,(如图3) 图3 此种情形下,物体刚运动到传送带上时将做加速度大小为 的减速运动,假定物体一直减速到离开传送带,则其离开传送带时的速度为 ,显然: v ≥ 0,即时,物体将一直做减速运动直到从传送带的另一端离开传送带,物体最终离开传送带时的速度。 若 v不能取得实数,即时,物体将不会从传送带的另一端离开而从进入端离开,其可能的运动情形有: (1)当时,物体先沿V0方向减速到零,再反向加速直至从放入端离开传送带,物体最终离开传送带时的速度大小。 (2)当时,物体先沿V0方向减速到零,再沿V0反向加速到与传送带速度相等,最后匀速直至从放入端离开传送带,物体最终离开传送带时的速度大小。 (ii)传送带变速运动 为了简化讨论,设传送带的初速度为零,物体与传送带之间的动摩擦因数为μ,两传动轮之间的距离为L,物体置于传送带一端的初速度为V0,传送带的加速度为,物体的加速度为。 ①.如图4所示,物体从静止开始加速即时,有两种情况: 图4 (1)若,物体与传送带以相同的加速度一起加速,二者相对静止,最终物体离开传送带时的速度。 (2).若,两者间出现相对滑动,物体加速运动的加速度为,物体离开传送带时的速度,此时传送带的速度为。 ②.当且与传送带加速方向相同时 设二者刚好达到共同速度V共,由有,故物体在t时间内通过的位移满足: (1).时,物体先减速到与传送带速度相等,之后再加速,而加速时同样有与①中类似的两种情况,但物体的终态速度与①中不同,需从两阶段的运动规律来计算。 A: 若,此后物体与传送带以共同的加速度运动,离开传送带时的速度v满足,如图5。 图5 B:若,物体将以加速度通过剩余的路程,其终态的速度满足 (2).当时,物体一直以加速度减速运动,离开传送带时的速度为,此过程经历的时间,终态下传送带的速度为。 ③.当且与传送带加速方向反向时,如图6. 图6 此种情形下,物体刚运动到传送带上时将做加速度大小为 的减速运动,假定物体一直减速到离开传送带,则其离开传送带时的速度为 ,显然: v ≥ 0,即v0≥时,物体将一直做减速运动直到从传送带的另一端离开传送带,物体最终离开传送带时的速度。 若 v不能取得实数,即时,物体将不会从传送带的另一端离开而从进入端离开,其可能的运动情形有: (1)当时,。物体先沿v0方向减速到零,再沿v0反向加速到与传送带速度相等,最后随传送带直至从放入端离开传送带。设二者刚好达到共同速度v共,由有,故物体在t时间内通过的位移,物体最终离开传送带时的速度大小满足。 (2)当时,物体先沿V0 方向减速到零,再反向加速直至从放入端离开传送带,物体最终离开传送带时的速度大小 2.斜置传送带 (I)物块受力 物块通常只受三个力的作用:重力、支持力、滑动摩擦力或静摩擦力 (II).运动分析 设传送带两定滑轮间的距离为L,带与水平面的夹角为θ ,物与带之间的动摩擦因数为μ,物体置与带的一端,初速度为v0,传送带的速度为v带。 (i)如图7,物体置于传送带的上端且v0=0 图7 ①当传送带顺时针转动时 若传送带足够长时,物块沿传送带从顶端A运动到底端B需经历两个阶段: 第一阶段 物块有相对传送带有向上的相对速度,受到滑动摩擦力方向沿传送带向下,受力如图8所示,可知 a=gsinθ+μgcosθ。物体将做初速度为零的加速度a=gsinθ+μgcosθ的匀加速直线运动,直到物体和传送带具有相同的速度。 图8 第二阶段 当物体加速到与传送带有相同速度时,进入第二阶段,受力如图9所示,又存在两种情况: 图9 (A).若mgsinθ≤fmax=μmgcosθ即μ≥tanθ时 物体有相对传送带向下滑动的趋势,而不是相对滑动,摩擦力不但由滑动摩擦力突变为静摩擦力,而且方向也发生了突变。此时有mgsinθ= f(静摩擦力),物体将保持和传送带相同的速度做匀速直线运动直到B端。 (B).若mgsinθ>Fmax=μmgcosθ即μ<tanθ时 物体将相对传送带向下滑动,滑动摩擦力的方向将发生突变,滑动摩擦力的方向由原来的沿斜面向下突变为沿斜面向上。可知 a=gsinθ-μgcosθ。物体将以第一阶段的末速度即传送带的速度为初速度,以a=gsinθ-μgcosθ做匀加速直线运动直到B端。 若传送带较短时,物体可能只经历第一个阶段,当物块匀加速运动到B端时速度恰好等于传送带的速度时,,故当时物块只经历第一个阶段,当时物块在整个运动过程中经历两个阶段。 ②当传送带逆时针转动时 物体有相对传送带有向下的相对速度,物体受到滑动摩擦力方向沿传送带向上,物体受力也如图9,此时物体的运动情况如下: (A)当mgsinθ<μmgcosθ即μ>tanθ时,物体将直接从传送带上端离开传送带。 (B)当mgsinθ=μmgcosθ即μ=tanθ时,物体将相对地面静止。 (C)当mgsinθ>μmgcosθ即μ<tanθ时,可知a=gsinθ-μgcosθ物体在全过程中做初速度为零的、加速度为a=gsinθ-μgcosθ的匀加速直线运动直到B端。 (ii)如图7,物体置于传送带的上端且V0≠ 0、方向沿传送带向下 ①当传送带顺时针转动时 物块一定从传送带底端离开传送带,若传送带足够长时,物块沿传送带从顶端A运动到底端B需经历两个阶段或一个阶段: (A) 当mgsinθ≤μmgcosθ即μ≥tanθ时: 若v0>v带 ,物块受力如图9,物块将先以加速度a=μgcosθ-gsinθ做匀减速运动;速度减小到与传送带速度相等后,滑动摩擦力突变为静摩擦力,方向不变,物块再做匀速运动。学 ] 若v0=v带 , 物块受到如图9所示的静摩擦力,直接从传送带顶端匀速运动到底端。 若v0查看更多
相关文章
- 当前文档收益归属上传用户