【物理】2018届二轮复习第3讲力与曲线运动学案
第3讲 力与曲线运动
¥ 考点一 抛体运动
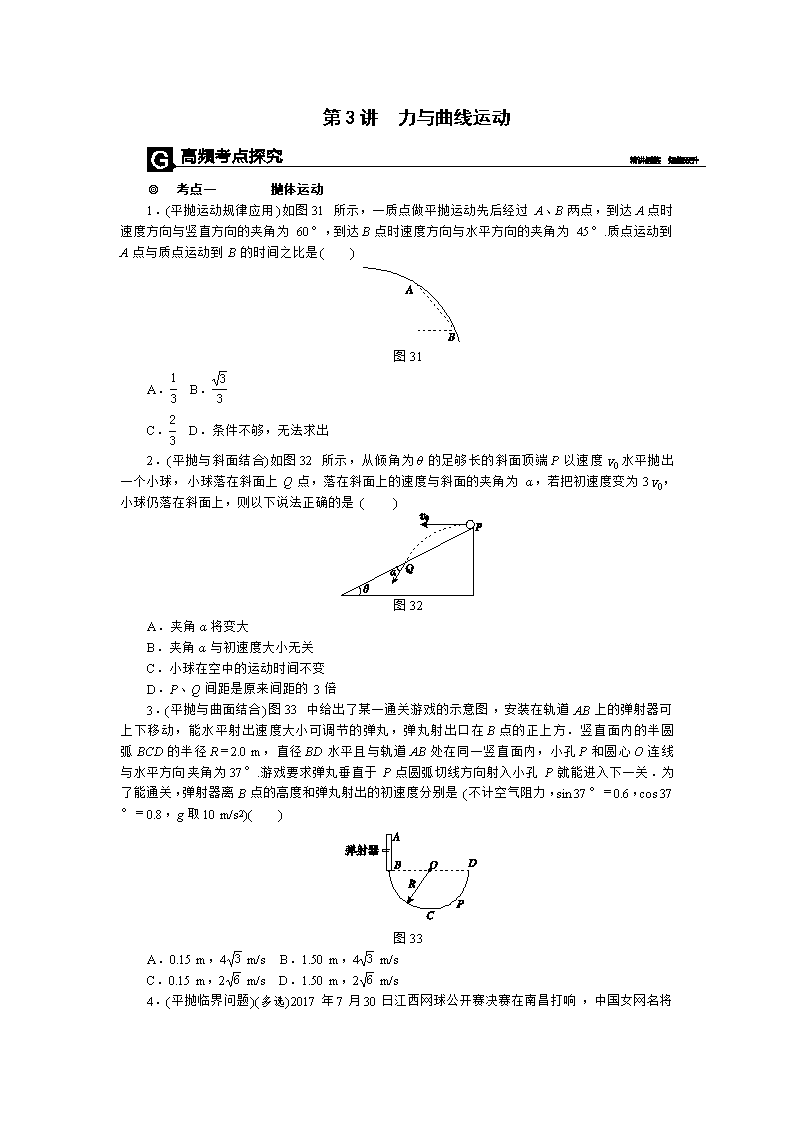
1.(平抛运动规律应用)如图31所示,一质点做平抛运动先后经过A、B两点,到达A点时速度方向与竖直方向的夹角为60°,到达B点时速度方向与水平方向的夹角为45°.质点运动到A点与质点运动到B的时间之比是( )
图31
A. B.
C. D.条件不够,无法求出
2.(平抛与斜面结合)如图32所示,从倾角为θ的足够长的斜面顶端P以速度v0水平抛出一个小球,小球落在斜面上Q点,落在斜面上的速度与斜面的夹角为α,若把初速度变为3v0,小球仍落在斜面上,则以下说法正确的是( )
图32
A.夹角α将变大
B.夹角α与初速度大小无关
C.小球在空中的运动时间不变
D.P、Q间距是原来间距的3倍
3.(平抛与曲面结合)图33中给出了某一通关游戏的示意图,安装在轨道AB上的弹射器可上下移动,能水平射出速度大小可调节的弹丸,弹丸射出口在B点的正上方.竖直面内的半圆弧BCD的半径R=2.0 m,直径BD水平且与轨道AB处在同一竖直面内,小孔P和圆心O连线与水平方向夹角为37°.游戏要求弹丸垂直于P点圆弧切线方向射入小孔P就能进入下一关.为了能通关,弹射器离B点的高度和弹丸射出的初速度分别是(不计空气阻力,sin 37°=0.6,cos 37°=0.8,g取10 m/s2)( )
图33
A.0.15 m,4 m/s B.1.50 m,4 m/s
C.0.15 m,2 m/s D.1.50 m,2 m/s
4.(平抛临界问题)(多选)
2017年7月30日江西网球公开赛决赛在南昌打响,中国女网名将彭帅夺得冠军.如图34所示为彭帅将球在边界A处正上方B点水平向右击出,球恰好过网C落在D处(不计空气阻力)的示意图,已知AB=h1,AC=x,CD=,网高为h2,下列说法中正确的是( )
图34
A.击球点高度h1与球网的高度h2之间的关系为h1=1.8h2
B.若保持击球高度不变,球的初速度v0只要不大于,就一定落在对方界内
C.任意降低击球高度(仍高于h2),只要击球初速度合适(球仍水平击出),球一定能落在对方界内
D.任意增加击球高度,只要击球初速度合适(球仍水平击出),球一定能落在对方界内
归纳
1.平抛运动可以分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动.解答平抛运动的常用方法如下:
2.有用结论
(1)飞行时间:t=,取决于下落高度h,与初速度v0无关.
(2)水平射程:x=v0t=v0,由初速度v0和下落高度h共同决定,与其他因素无关.
(3)落地速度:v==,与水平方向的夹角的正切tan α==,所以落地速度只与初速度v0和下落高度h有关.
(4)某时刻速度的反向延长线通过此时水平位移的中点.
¥ 考点二 圆周运动的动力学问题
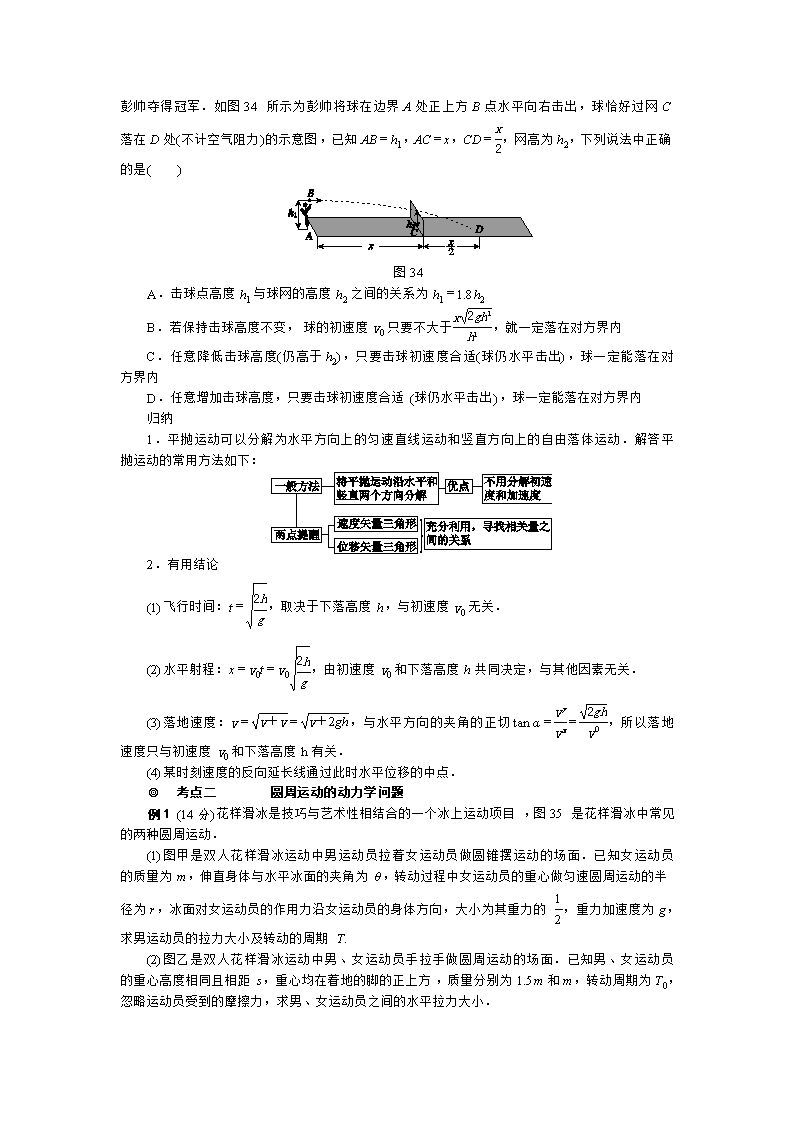
例1 (14分)花样滑冰是技巧与艺术性相结合的一个冰上运动项目,图35是花样滑冰中常见的两种圆周运动.
(1)图甲是双人花样滑冰运动中男运动员拉着女运动员做圆锥摆运动的场面.已知女运动员的质量为m,伸直身体与水平冰面的夹角为θ,转动过程中女运动员的重心做匀速圆周运动的半径为r,冰面对女运动员的作用力沿女运动员的身体方向,大小为其重力的,重力加速度为g,求男运动员的拉力大小及转动的周期T.
(2)图乙是双人花样滑冰运动中男、女运动员手拉手做圆周运动的场面.已知男、女运动员的重心高度相同且相距s,重心均在着地的脚的正上方,质量分别为1.5m和m,转动周期为T0,忽略运动员受到的摩擦力,求男、女运动员之间的水平拉力大小.
甲
乙
图35
[解答步骤规范]
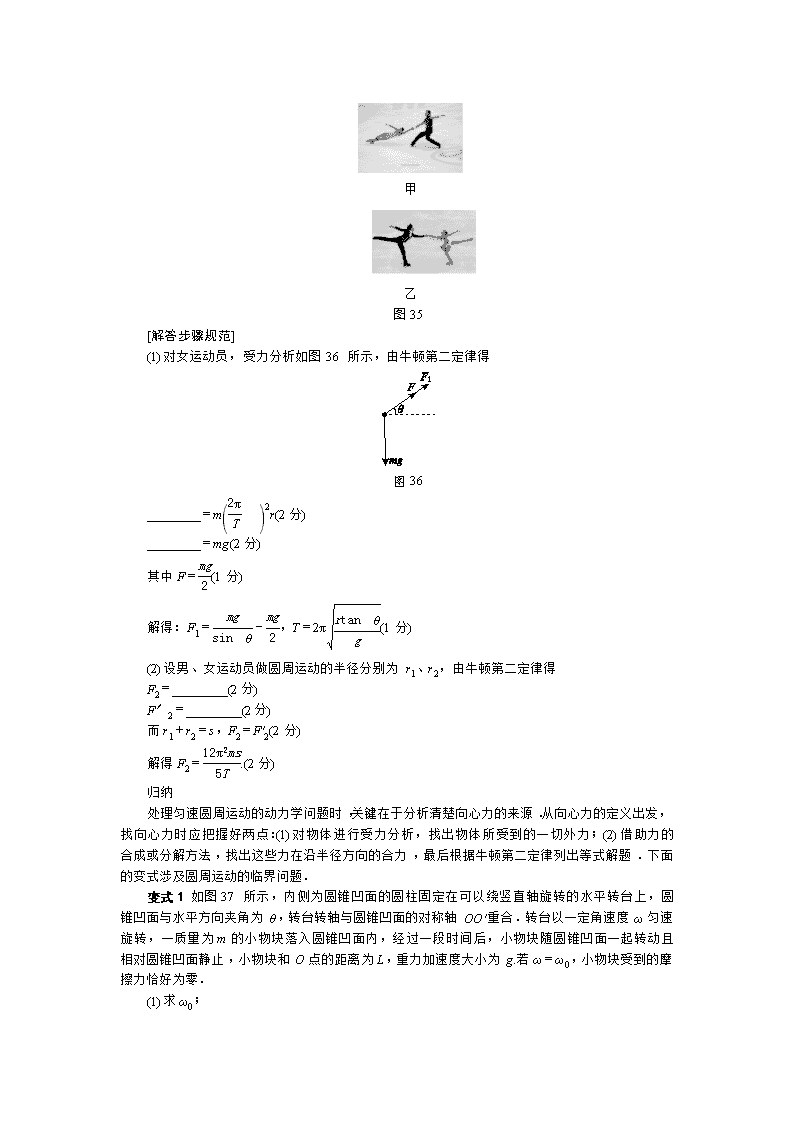
(1)对女运动员,受力分析如图36所示,由牛顿第二定律得
图36
________=mr(2分)
________=mg(2分)
其中F=(1分)
解得:F1=-,T=2π(1分)
(2)设男、女运动员做圆周运动的半径分别为r1、r2,由牛顿第二定律得
F2=________(2分)
F′2=________(2分)
而r1+r2=s,F2=F′2(2分)
解得F2=.(2分)
归纳
处理匀速圆周运动的动力学问题时,关键在于分析清楚向心力的来源.从向心力的定义出发,找向心力时应把握好两点:(1)对物体进行受力分析,找出物体所受到的一切外力;(2)借助力的合成或分解方法,找出这些力在沿半径方向的合力,最后根据牛顿第二定律列出等式解题.下面的变式涉及圆周运动的临界问题.
变式1 如图37所示,内侧为圆锥凹面的圆柱固定在可以绕竖直轴旋转的水平转台上,圆锥凹面与水平方向夹角为θ,转台转轴与圆锥凹面的对称轴OO′重合.转台以一定角速度ω匀速旋转,一质量为m的小物块落入圆锥凹面内,经过一段时间后,小物块随圆锥凹面一起转动且相对圆锥凹面静止,小物块和O点的距离为L,重力加速度大小为g.若ω=ω0,小物块受到的摩擦力恰好为零.
(1)求ω0;
(2)若ω=(1±k)ω0,且0
1).若该天体有一颗近地环绕卫星,则近地环绕卫星的周期为( )
A.·T B.·T
C.·T D.·T
归纳
万有引力与重力的关系:①在星球表面处,考虑星球自转,则重力是万有引力的一个分力,不考虑星球自转,则重力约等于万有引力;在星球表面上空某处,万有引力总是等于重力.②星球表面上空的重力加速度g与(R+h)2成反比,这是一个非常有用的结论.③在星球内部的隧道里,重力加速度g与其到地心的距离x成正比.
变式 (多选)若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,引力常量为G.则下列说法正确的是( )
A.月球表面的重力加速度g月=
B.月球的质量m月=
C.月球的第一宇宙速度v=
D.月球的平均密度ρ=
考向3 多星问题
例4 据报道,一个国际研究小组借助于智利的天文望远镜,观测到了一组双星系统,它们绕两者连线上的某点O做匀速圆周运动,如图39所示.假设此双星系统中体积较小的成员能“吸食”另一颗体积较大星体的表面物质,达到质量转移的目的,在演变过程中两者球心之间的距离保持不变,双星平均密度可视为相同.则在最初演变的过程中( )
图39
A.它们做圆周运动的万有引力保持不变
B.它们做圆周运动的角速度不断变小
C.体积较大的星体圆周运动轨迹的半径变大,线速度变大
D.体积较大的星体圆周运动轨迹的半径变小,线速度变大
归纳
由两颗或两颗以上的星体构成,忽略其他星体对它们的作用的一个孤立系统,俗称多星系统.①关于“多星”问题,运动过程构成稳定的位置关系,要抓住角速度的关系.②“多星”做圆周运动的向心力由它们的万有引力的合力提供,需要进行受力分析,对力有效地合成.③应注意的是“多星中的某星球”做圆周运动的轨道半径和该星与其他星球的距离是两个数量和物理意义都不同的概念.
来源
竖直平面的圆周运动模型
统计分析
2016·全国卷Ⅲ第20题
1.(多选)[2016·全国卷Ⅲ] 如图所示,一固定容器的内壁是半径为R的半球面;在半球面水平直径的一端有一质量为m的质点P.它在容器内壁由静止下滑到最低点的过程中,克服摩擦力做的功为W.重力加速度大小为g.设质点P在最低点时,向心加速度的大小为a,容器对它的支持力大小为N,则( )
A.a=
B.a=
C.N=
D.N=
通过对以往高考真题的统计可以看出,竖直平面中的圆周运动是近几年高考考查的热点,综合性强,能力要求高,可以考查受力分析和运动分析、牛顿运动定律、机械能、功能关系等多方面问题,所以,竖直平面中的圆周运动是一个非常重要的模型.从应用解题来看,关注运动的特殊状态,往往应用向心力公式研究圆周运动的最高点或最低点,涉及临界问题;关注运动的某一过程或多个过程,往往应用动能定理或机械能守恒定律进行研究
2017·全国卷Ⅱ第17题
2.[2017·全国卷Ⅱ] 如图所示,半圆形光滑轨道固定在水平地面上,半圆的直径与地面垂直.一小物块以速度v从轨道下端滑入轨道,并从轨道上端水平飞出,小物块落地点到轨道下端的距离与轨道半径有关,此距离最大时对应的轨道半径为(重力加速度大小为g)( )
A. B.
C. D.
2016·全国卷Ⅲ第24题
3.[2016·全国卷Ⅲ] 如图所示,在竖直平面内有由圆弧AB和圆弧BC组成的光滑固定轨道,两者在最低点B平滑连接.AB弧的半径为R,BC弧的半径为.一小球在A点正上方与A相距处由静止开始自由下落,经A点沿圆弧轨道运动.
(1)求小球在B、A两点的动能之比;
(2)通过计算判断小球能否沿轨道运动到C点.
【模型核心归纳】
分类
轻绳模型(最高点无支撑)
轻杆模型(最高点有支撑)
实例
球与绳连接、水流星、翻滚过山车
球与杆连接、球过竖直管道、套在圆环上的物体等
图示
在最高点受力
重力、弹力F弹向下或等于零,mg+F弹=m
重力,弹力F弹向下、向上或等于零
mg±F弹=m
恰好过最高点
F弹=0,mg=m,v=
在最高点速度不能为零
v=0,mg=F弹
在最高点速度可为零
示例 (多选)如图310所示,一质量为m的小球置于半径为R的光滑竖直圆轨道最低点A处,B为轨道最高点,C、D为圆的水平直径两端点.轻质弹簧的一端固定在圆心O点,另一端与小球拴接,已知弹簧的劲度系数为k=,原长为L=2R,弹簧始终处于弹性限度内,若给小球一水平初速度v 0,已知重力加速度为g,则( )
图310
A.无论v 0多大,小球均不会离开圆轨道
B.若< v 0<,则小球会在B、D间脱离圆轨道
C.只要v 0>,小球就能做完整的圆周运动
D.若小球能做完整的圆周运动,则小球与轨道间最大压力与最小压力之差与v 0无关
拓展1 (多选)开口向上的半球形曲面的截面如图311所示,直径AB水平.一物块(可视为质点)在曲面内A点以某一速率开始下滑,曲面内各处动摩擦因数不同,因摩擦作用物块下滑过程速率保持不变.在物块下滑的过程中,下列说法正确的是( )
图311
A.物块运动过程中加速度始终为零
B.物块所受合外力大小不变,方向时刻在变化
C.滑到最低点C时,物块所受重力的瞬时功率达到最大
D.物块所受摩擦力大小逐渐变小
拓展2 如图312所示,空间有一水平向右的匀强电场,长度为r的绝缘细线一端固定在O点,另一端连接一质量为m、电荷量为+q的小球,小球静止在P点,AB沿竖直方向,且OP与AB的夹角θ=37°.不计空气阻力.已知重力加速度为g,sin 37°=0.6,cos 37°=0.8.下列选项正确的是( )
图312
A.电场强度E=
B.电场强度E=
C.若要使小球从P点出发做完整的圆周运动,小球初速度v 0≥
D.若要使小球从P点出发做完整的圆周运动,小球初速度v 0≥
拓展3 如图313甲所示,质量m=1 kg的物体以v 0=4 m/s的初速度从水平面上的某点向右运动并冲上半径R=0.1 m的竖直光滑半圆环.物体与水平面间有摩擦.(g取10 m/s2)
(1)物体能从M点飞出,落到水平面时落点到N点的距离的最小值为多大?
(2)设出发点到N点的距离为x,物体从M点飞出后,落到水平面时落点到N点的距离为y,作出y2随x变化的关系图像如图乙,求物体与水平面间的动摩擦因数μ;
(3)欲使物体不脱离半圆轨道,则物体的出发点到N点间的距离应满足什么条件?
图313
第3讲 力与曲线运动
高频考点探究
考点一
1.B [解析] 设初速度为v0,将A、B两点的速度分解,在A点,有tan(90°-60°)==,解得tA=;在B点,有tan 45°==,解得tB=.故=,故B正确,A、C、D错误.
2.B [解析] 由图可知,tan(α+θ)==,而tan θ===,可知tan(α+θ)=2tan θ,α与初速度大小无关,选项A错误,选项B正确;斜面倾角的正切值tan θ==,解得t=,初速度变为原来的3倍,则运动时间变为原来的3倍,选项C错误;P、Q间距s==,初速度变为原来的3倍,t变为原来的3倍,则s变为原来的9倍,选项D错误.
3.A [解析] 设弹射器离B点的高度为h,弹丸射出的初速度为v0,弹丸做平抛运动,有x=v0t,y=gt2,其中x=R+Rcos 37°,y=h+Rsin 37°,R=2 m,又知弹丸垂直于P点圆弧切线方向射入小孔P,则tan 37°==,联立解得v0=4 m/s,h=0.15 m,选项A正确.
4.AD [解析] 由平抛运动规律可知h1=gt,1.5x=v0t1,h1-h2=gt,x=v0t2,得h1=1.8h2,A正确;若保持击球高度不变,球的初速度v0较小时,球可能会触网,B错误;任意降低击球高度(仍高于h2),若初速度合适,球可能不会触网,但球可能会出界,C错误;任意增加击球高度,只要击球初速度合适,使球的水平位移小于2x,一定能落在对方界内,D正确.
考点二
例1 (1)(F+F1)cos θ (F+F1)sin θ (2)1.5mr1 mr2
例1变式1 (1) (2)略
[解析] (1)当ω=ω0时,小物块受重力和支持力,由牛顿第二定律可得
mgtan θ=mωLcos θ
解得ω0=.
(2)当ω=(1+k)ω0时,小物块做圆周运动所需向心力变大,则摩擦力方向沿圆锥面向下,对小物块受力分析可得
水平方向:FNsin θ+fcos θ=mω2Lcos θ
竖直方向:FNcos θ-fsin θ=mg
解得f=k(2+k)mgsin θ
当ω=(1-k)ω0
时,小物块做圆周运动所需向心力变小,则摩擦力方向沿圆锥面向上,对小物块受力分析有
水平方向:FNsin θ-fcos θ=mω2Lcos θ
竖直方向:FNcos θ+fsin θ=mg
解得f=k(2-k)mgsin θ.
例1变式2 BD [解析] 对A和B,摩擦力提供向心力,转台对A、B的摩擦力分别为m·2rω2、2m·rω2,选项A错误,B正确;对A,μmg≥2mω2r,解得ω≤,选项C错误;在转台的角速度逐渐增大的过程中,A先达到最大静摩擦力,A比B先滑动,选项D正确.
考点三
例2 BCD [解析] “天舟一号”的轨道半径小于地球同步卫星的轨道半径,所以“天舟一号”比同步卫星转动得快,角速度大,周期短,而地球自转的角速度和周期与地球同步卫星的相同,所以“天舟一号”的角速度比地球自转角速度大,周期短,故A错误,C正确.“天舟一号”的轨道半径大于近地卫星的轨道半径,所以“天舟一号”比近地卫星的线速度小,向心加速度小,近地卫星的线速度就是第一宇宙速度,近地卫星的向心加速度等于地面的重力加速度,所以“天舟一号”的线速度小于第一宇宙速度,向心加速度小于地面的重力加速度,故B、D正确.
例2变式1 ABC [解析] 一颗卫星与地球赤道圆的直径的两端连线的交角小于180°,至少需要2颗卫星才能传到直径的两端,选项A正确;当两颗卫星的信号恰好到达直径两端时,卫星的轨道半径为R,此时向心加速度最大,且amax=g=4.9 m/s2,最小周期Tmin=2π=2π=8.53×103 s,选项C正确,选项D错误;传播的最短路径s=4R,最短时间tmin==8.52×10-2 s,选项B正确.
例2变式2 BC [解析] 飞船在返回地球的过程中需要控制速度,机械能不守恒,选项A错误;根据万有引力提供向心力,有G=mr,解得T=,可知=,国际空间站的轨道半径约为6800 km,地球同步卫星的轨道半径约为42 400 km,地球同步卫星的周期为24 h,可得国际空间站的运行周期约为90 min,选项B正确;地球的第一宇宙速度是所有地球卫星的最大环绕速度,所以国际空间站的速度小于地球的第一宇宙速度,选项C正确;返回时,需先让飞船与国际空间站脱离,然后减速,即可下降,选项D错误.
例3 D [解析] 在“赤道”处,mg+m=G,在“北极点”,kmg=G,联立可得=;对近地环绕卫星,=m′,解得周期T0=·T,选项D 正确.
例3变式 ABC [解析] 平抛运动的时间t=.再根据h=g月t2,得g月=,选项A正确;由g月=与g月=,可得:m月=,选项B正确;第一宇宙速度:v==解得v=,选项C正确;月球的平均密度ρ==,选项D错误.
例4 C [解析] 设体积较小的星体质量为m1,轨道半径为r1,体积较大的星体质量为m2,轨道半径为r2,双星间的距离为L.转移的质量为Δm.则它们之间的万有引力为F=G
,根据数学知识得知,随着Δm的增大,F先增大后减小,选项A错误.对小星体:G=(m1+Δm)ω2r1①,对大星体:G=(m2-Δm)ω2r2②,联立①②解得:ω=,总质量m1+m2不变,两者距离L不变,则角速度ω不变,选项B错误.由②得:G=ω2r2,ω、L、m1均不变,Δm增大,则r2 增大,即体积较大的星体圆周运动轨迹半径变大,由v2=ωr2得线速度v2也增大,选项C正确,选项D错误.
热点模型解读
1.AC [解析] 质点P下滑到底端的过程,由动能定理得mgR-W=mv2-0,可得v2=,所以a==,A正确,B错误;在最低点,由牛顿第二定律得N-mg=m,故N=mg+m=mg+·=,C正确,D错误.
2.B [解析] 物块上升到最高点的过程,机械能守恒,有mv2=2mgr+mv,由平抛运动规律,水平方向,有x=v1t,竖直方向,有2r=gt2,解得x=,当r=时,x最大,B正确.
3.(1)5 (2)能
[解析] (1)设小球的质量为m,小球在A点的动能为EkA,由机械能守恒得EkA=mg ①
设小球在B点的动能为EkB,同理有EkB=mg ②
由①②式得=5 ③
(2)若小球能沿轨道运动到C点,小球在C点所受轨道的正压力N应满足N≥0 ④
设小球在C点的速度大小为vC,由牛顿运动定律和向心加速度公式有N+mg= ⑤
由④⑤式得,vC应满足mg≤m ⑥
由机械能守恒有mg=mv ⑦
由⑥⑦式可知,小球恰好可以沿轨道运动到C点.
示例 ACD [解析] 当小球恰好到达最高点时,合力最小值Fm=mg-kR=m,则最小速度vm=0,小球受弹簧弹力作用,小球在任何位置都不会脱离圆轨道,选项A正确,选项B错误;从最低点到最高点,有-2mgR=mv-mv,则v0最小值为,只要小球初速度v0>
,小球就能做完整的圆周运动,选项C正确;在最低点,FN1-mg-kR=m,在最高点,FN2+mg-kR=m,又-2mgR=mv-mv,则两弹力之差ΔFN=6mg,其大小与初速度v0无关,选项D正确.
示例拓展1 BD [解析] 物块做匀速圆周运动,物块的向心加速度不为零,选项A错误;物块所受合外力F=m,大小不变,方向时刻在变化,选项B正确;重力的瞬时功率P=mgvy,物块在最低点C,竖直分速度为零,所以重力的瞬时功率为零,选项C错误;物块在下滑的过程中的摩擦力大小与重力在圆弧切线方向上的分力大小相等,重力在圆弧切线方向上的分力减小,所以摩擦力逐渐减小,选项D正确.
示例拓展2 AD [解析] 当小球静止在P点时,受力如图,由平衡条件得=tan 37°,则E=,选项A正确;若要使小球做完整的圆周运动,则小球必须能通过图中的Q点,Q点的最小速度为vQ,则=m,设当小球从P点出发的速度为vP时,小球恰好能到达Q点,根据动能定理有-·2r=mv-mv,解得vP=,选项D正确.
示例拓展3 (1)0.2 m (2)0.18 (3)3.9 m≤x<4.4 m或0≤x≤3.1 m
[解析] (1)物体能从M点飞出,则
mg=m
解得vmin=
ymin=vmint
2R=gt2
解得ymin=2R=0.2 m.
(2)对物体从出发点到M点过程,由动能定理得
-μmgx-mg·2R=mv-mv
y=vMt
2R=gt2
联立解得y2=-μx+
由图知-μ=
解得μ=0.18.
(3)当物体恰好不会在M到N点之间离开半圆轨道,即物体恰好从M点飞出时,有ymin=0.2 m
解得xmax=3.1 m
当物体刚好至半圆轨道最右侧速度减为零时,由动能定理得
-μmgxmin-mgR=0-mv
恰到N点时速度减为零,有
-μmgx0=0-mv
解得xmin=3.9 m
x0=4.4 m
综上可得3.9 m≤x<4.4 m或0≤x≤3.1 m.