高中物理磁场练习题及答案
磁场练习题及答案1、指南针静止时,其位置如图中虚线所示.若在其上方放置一水平方向的导线,并通以恒定电流,则指南针转向图中实线所示位置.据此可能是:BA.导线南北放置,通有向北的电流B.导线南北放置,通有向南的电流C.导线东西放置,通有向西的电流 D.导线东西放置,通有向东的电流2、北半球某地,地磁场的磁感应强度B=5×10-5T,磁倾角(磁感线与水平方向的夹角)为60°。长200m的输电导线中通有从西向东I=100A的恒定电流。该段导线受的安培力大小和方向为:AA.1N,向北与水平面成30°斜向上方B.0.5N,向北与水平面成30°斜向上方C.0.5N,向南与水平面成30°斜向下方D.0.87N,向南与水平面成30°斜向下方3、赤道附近地磁场方向向北,同时存在方向竖直向下的电场,若在该处发射一电子,电子沿直线飞行而不发生偏转。则该电子的飞行方向为:AA.水平向东B.水平向西C.竖直向上D.竖直向下v4、在赤道上空有一小磁针处于水平静止状态,突然发现小磁针N极向东偏转,由此可知:DA.一定是小磁针正东方向有一条形磁铁的N极靠近小磁针B.一定是小磁针正北方向有一条形磁铁的S极靠近小磁针C.可能是小磁针正上方有电子流自北向南水平通过D.可能是小磁针正上方有电子流自南向北水平通过xyzOFI5、每时每刻都有大量带电的宇宙射线向地球射来,幸好地球磁场可以有效地改变这些宇宙射线中大多数射线粒子的运动方向,使它们不能到达地面,这对地球上的生命有十分重要的意义.假设有一个带正电的宇宙射线粒子正垂直于地面向赤道射来(如图,地球由西向东转,虚线表示地球自转轴,上方为地理北极),在地球磁场的作用下,它将如何偏转:AA.向东B.向南C.向西D.向北6、在XOY平面中有一通电直导线与OX、OY轴相交,导线中电流方向如图所示.该区域有匀强磁场,通电直导线所受磁场力的方向与OZ轴的正方向相同.该磁场的磁感应强度的方向可能是:ABA.沿X轴负方向B.沿Y轴负方向OO/θ/θ/BC.沿Z轴正方向D.沿Z轴负方向7、如图所示,质量为60g的金属棒长为L1=20cm,棒两端与长为L2=30cm的细软金属线相连,吊在磁感应强度B=0.5T、竖直向上的匀强磁场中。当金属棒中通过稳恒电流I后,金属棒向纸外摆动,摆动过程中的最大偏角θ=60°(取g=10m/s2),则下列说法中正确的是:BDA.金属棒中电流方向水平向右,电流大小为6AB.金属棒中电流方向水平向右,电流大小为2AC.当偏角θ=60°时,金属棒受到的合力为零D.金属棒在摆动过程中动能的最大值为2.78×10-2J8、质量为m长为L的导体棒电阻为R,初静止于光滑的水平轨道上,电源电动势为E,内阻不计.匀强磁场的磁感强度为B,其方向与轨道平
面成θ角斜向上方,电键闭合后导体棒开始运动.BDA.导体棒向左运动B.电键闭合瞬间导体棒MN所受安培力为BEL/RC.电键闭合瞬间导体棒MN所受安培力为BELsinθ/RD.电键闭合瞬间导体棒MN的加速度为BELsinθ/mR9、如图,长为2l的直导线拆成边长相等,夹角为的V形,并置于与其所在平面相垂直的匀强磁场中,磁感应强度为,当在该导线中通以电流强度为的电流时,该形通电导线受到的安培力大小为:CA.0B.0.5C.D.10、两根平行放置的长直导线a和b载有大小相等方向相反的电流,a受到的磁场力大小为F1.当加入一与导线所在平面垂直的匀强磁场后,a受到的磁场力大小变为F2,则此时b受到的磁场力大小变为:AA.F2B.C.D.11、两条直导线互相垂直,如图甲所示,但相隔一个小距离,其中一条AB是固定的,另一条CD能自由转动.当直流电流按图乙所示方向通入两条导线时,CD导线将:EA.不动B.顺时针方向转动,同时靠近导线ABC.顺时针方向转动,同时离开导线ABD.逆时针方向转动,同时离开导线ABE.逆时针方向转动,同时靠近导线AB12、如图所示,一边长为h的正方形线圈A,其中电流I大小和方向均保持不变,用两条长度恒为h的绝缘细绳静止悬挂于水平长直导线CD的正下方。当导线CD中无电流时,两细绳中张力均为T;当通过CD的电流为i时,两细绳中张力均降到;而当CD上的电流为时,两细绳中张力恰好为零。已知通电长直导线的磁场中某点的磁感应强度B与该点到导线的距离r成反比。由此可知,CD中的电流方向、CD中两次通入的电流大小之比分别为:ADA.电流方向向左B.电流方向向右C.电流大小之比D.电流大小之比13、下列说法中正确的是:ADA.若电荷在某处不受电场力作用,则该处电场强度一定为零B.若电荷在某处不受磁场力作用,则该处的磁感应强度一定为零C.将通电导体置于匀强磁场中,若导体长度和电流大小一定,那么导体所受的安培力大小也是一定的D.在磁感应强度为B的匀强磁场中,长为L、电流为I的通电直导线所受到的安培力的大小,介于零(含零)和BIL(含BIL)之间
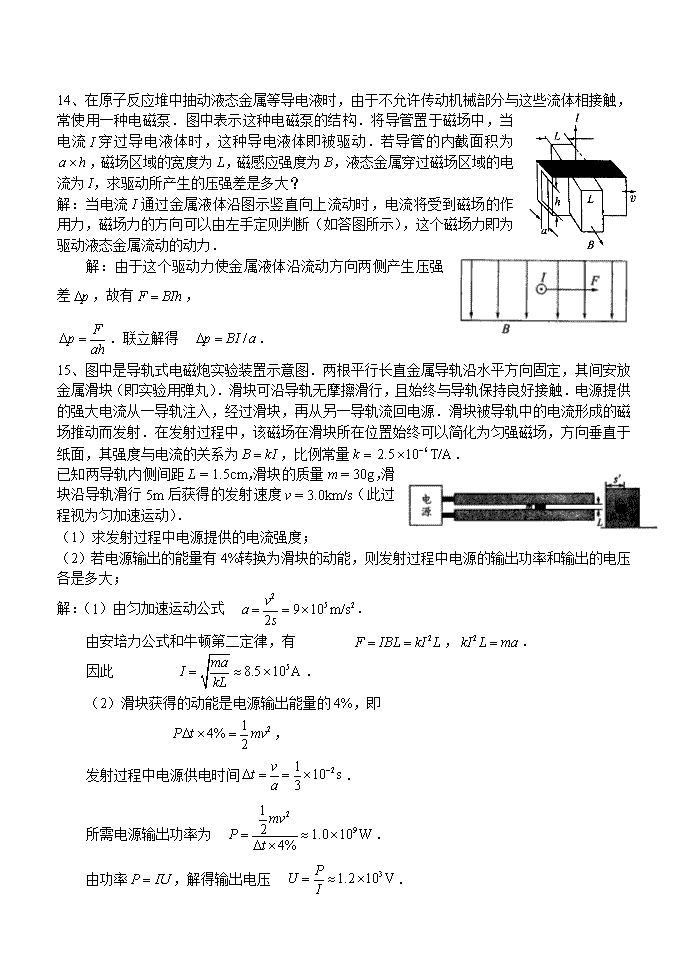
14、在原子反应堆中抽动液态金属等导电液时,由于不允许传动机械部分与这些流体相接触,常使用一种电磁泵.图中表示这种电磁泵的结构.将导管置于磁场中,当电流I穿过导电液体时,这种导电液体即被驱动.若导管的内截面积为,磁场区域的宽度为L,磁感应强度为B,液态金属穿过磁场区域的电流为I,求驱动所产生的压强差是多大?解:当电流I通过金属液体沿图示竖直向上流动时,电流将受到磁场的作用力,磁场力的方向可以由左手定则判断(如答图所示),这个磁场力即为驱动液态金属流动的动力.解:由于这个驱动力使金属液体沿流动方向两侧产生压强差,故有,.联立解得.15、图中是导轨式电磁炮实验装置示意图.两根平行长直金属导轨沿水平方向固定,其间安放金属滑块(即实验用弹丸).滑块可沿导轨无摩擦滑行,且始终与导轨保持良好接触.电源提供的强大电流从一导轨注入,经过滑块,再从另一导轨流回电源.滑块被导轨中的电流形成的磁场推动而发射.在发射过程中,该磁场在滑块所在位置始终可以简化为匀强磁场,方向垂直于纸面,其强度与电流的关系为,比例常量.已知两导轨内侧间距L=1.5cm,滑块的质量m=30g,滑块沿导轨滑行5m后获得的发射速度v=3.0km/s(此过程视为匀加速运动).(1)求发射过程中电源提供的电流强度;(2)若电源输出的能量有4%转换为滑块的动能,则发射过程中电源的输出功率和输出的电压各是多大;解:(1)由匀加速运动公式.由安培力公式和牛顿第二定律,有,.因此.(2)滑块获得的动能是电源输出能量的4%,即,发射过程中电源供电时间.所需电源输出功率为.由功率,解得输出电压.
16、如图所示,铜质导电板置于匀强磁场中,通电时铜板中电流方向向上.由于磁场的作用,则:AA.板左侧聚集较多电子,使b点电势高于a点电势IabB.板左侧聚集较多电子,使a点电势高于b点电势C.板右侧聚集较多电子,使a点电势高于b点电势D.板右侧聚集较多电子,使b点电势高于a点电势17、如图,空间有垂直于xoy平面的匀强磁场.t=0的时刻,一电子以速度v0经过x轴上的A点,方向沿x轴正方向.A点坐标为(,0),其中R为电子在磁场中做圆周运动的轨道半径.不计重力影响,则:ABDA.v0(-R/2,0)OxAy电子经过y轴时,速度大小仍为v0B.电子在时,第一次经过y轴C.电子第一次经过y轴的坐标为(0,)D.电子第一次经过y轴的坐标为(0,)Ox/cm2y/cm18、一个带电粒处于垂直于匀强磁场方向的平面内,在磁场力的作用下做圆周运动.要想确定带电粒子的电荷量与质量之比,则只需要知道:DA.运动速度v和磁感应强度BB.轨道半径R和磁感应强度BC.轨道半径R和运动速度vD.磁感应强度B和运动周期T19、如图所示,宽h=2cm的有界匀强磁场,纵向范围足够大,磁感应强度的方向垂直纸面向内,现有一群正粒子从O点以相同的速率沿纸面不同方向进入磁场,若粒子在磁场中做匀速圆周运动的半径均为r=5cm,则:ADA.右边界:-4cm
4cm和y<-4cm有粒子射出C.左边界:y>8cm有粒子射出D.左边界:0FNC.小球第一次到达M点的时间大于小球第一次到达N点的时间D.在磁场中小球能到达轨道另一端最高处,在电场中小球不能到达轨道另一端最高处50、质量为m,电荷量为q的微粒以速度v与水平方向成θ角从O点进入方向如图的正交的匀强电场和匀强磁场组成的混合场区,该微粒在电场力、磁场力和重力的共同作用下,恰好沿直线运动到A。下列说法中正确的是:CθAOvEBA.该微粒可能带正电荷也可能带负电荷B.微粒从O到A的运动可能是匀变速运动C.该磁场的磁感应强度大小为mg/(qvcosθ)D.该电场的场强为Bvcosθ51、如图所示,匀强磁场的边界为直角三角形abc,一束带正电的粒子以不同的速度v沿bc从b点射入磁场,不计粒子的重力,关于粒子在磁场中的运动情况下列说法中正确的是:CA.入射速度越大的粒子,其运动时间越长B.入射速度越大的粒子,其运动轨迹越长C.从ab边出射的粒子的运动时间都相等D.从ac边出射的粒子的运动时间都相等52、带电粒子以速度沿方向射人—横截面为正方形的区域,、均为该正方形两边的中点,如图所示,不计粒子的重力。当区域内有竖直方向的匀强电场时,粒子从点飞出,所用时间为;当区域内有垂直纸面向里的磁场感应强度为的匀强磁场时,粒子也从点飞出,所用时间为,下列说法正确的是:ADA.B.C.D.53、如图所示,匀强磁场的方向垂直纸面向里,一带电微粒从磁场边界d点垂直于磁场方向射入,沿曲线dpa打到屏MN上的a点,通过pa段用时为t.若该微粒经过p点时,与一个静止的不带电微粒碰撞并结合为一个新微粒,最终打到屏MN上,两个微粒所受重力均忽略.新微粒运动的:DA.轨迹为pb,至屏幕的时间将小于tB.轨迹为pc,至屏幕的时间将大于tC.轨迹为pb,至屏幕的时间将等于tOD.轨迹为pa,至屏幕的时间将大于t
54、如图所示的虚线区域内,充满垂直于纸面向里的匀强磁场和竖直向下的匀强电场。一带电粒子a(不计重力)以一定的初速度由左边界的O点射入磁场、电场区域,恰好沿直线由区域右边界的O′点(图中未标出)穿出。若撤去该区域内的磁场而保留电场不变,另一个同样的粒子b(不计重力)仍以相同初速度由O点射入,从区域右边界穿出,则粒子b:CA.穿出位置一定在O′点下方B.穿出位置一定在O′点上方C.运动时,在电场中的电势能一定减小D.在电场中运动时,动能一定减小55、图是质谱仪的工作原理示意力。带电粒子被加速电场加速后,进入速度选择器。速度选择器内相互正交的匀强磁场和匀强电场的强度分别为B和E。平板S上有可让粒子通过的狭缝P和记录粒子位置的胶片A1A2。平板S下方有强度为B0的匀强磁场。下列表述正确的是:ABCA.质谱仪是分析同位素的重要工具B.速度选择器中的磁场方向垂直纸面向外C.能通过狭缝P的带电粒子的速率等于E/BD.粒子打在胶片上的位置越靠近狭缝P,粒子的荷质比越小abNS血流测电势差56、医生做某些特殊手术时,利用电磁血流计来监测通过动脉的血流速度。电磁血流计由一对电极a和b以及磁极N和S构成,磁极间的磁场是均匀的。使用时,两电极a、b均与血管壁接触,两触点的连线、磁场方向和血流速度方向两两垂直,如图所示。由于血液中的正负离子随血流一起在磁场中运动,电极a、b之间会有微小电势差。在达到平衡时,血管内部的电场可看作是匀强电场,血液中的离子所受的电场力和磁场力的合力为零。在某次监测中,两触点的距离为3.0mm,血管壁的厚度可忽略,两触点间的电势差为160µV,磁感应强度的大小为0.040T。则血流速度的近似值和电极a、b的正负为:AA.1.3m/s,a正、b负B.2.7m/s,a正、b负C.1.3m/s,a负、b正D.2.7m/s,a负、b正B~57、回旋加速器是用来加速带电粒子的装置,如图所示.它的核心部分是两个D形金属盒,两盒相距很近,分别和高频交流电源相连接,两盒间的窄缝中形成匀强电场,使带电粒子每次通过窄缝都得到加速。两盒放在匀强磁场中,磁场方向垂直于盒底面,带电粒子在磁场中做圆周运动,通过两盒间的窄缝时反复被加速,直到达到最大圆周半径时通过特殊装置被引出。如果用同一回旋加速器分别加速氚核()和α粒子()比较它们所加的高频交流电源的周期和获得的最大动能的大小,有:BA.加速氚核的交流电源的周期较大,氚核获得的最大动能也较大B.加速氚核的交流电源的周期较大,氚核获得的最大动能较小C.加速氚核的交流电源的周期较小,氚核获得的最大动能也较小D.加速氚核的交流电源的周期较小,氚核获得的最大动能较大
58、回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形金属盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示。设D形盒半径为R。若用回旋加速器加速质子时,匀强磁场的磁感应强度为B,高频交流电频率为f。则下列说法正确的是:ABA.质子被加速后的最大速度不可能超过2πfRB.质子被加速后的最大速度与加速电场的电压大小无关C.只要R足够大,质子的速度可以被加速到任意值D.不改变B和f,该回旋加速器也能用于加速α粒子59、电磁流量计广泛应用于测量可导电液体(如污水)在管中的流量(在单位时间内通过管内横截面的流体的体积)。为了简化,假设流量计是如图16—28所示的横截面为长方形的一段管道,其中空部分的长、宽、高分别为图中的a、b、c流量计的两端与输送流体的管道相连接(图中虚线)。图中流量计的上下两面是金属材料,前后两面是绝缘材料。现于流量计所在处加磁感强度B的匀强磁场,磁场方向垂直于前后两面。当导电流体稳定地流经流量计时,在管外将流量计上、下两表面分别与一串接了电阻R的电流表的两端连接,I表示测得的电流值。已知流体的电阻率为ρ,不计电流表的内阻,则可求得流量为:AA.B.C.D.60、某制药厂的污水处理站的管道中安装了如图所示的流量计,该装置由绝缘材料制成,长、宽、高分别为a、b、c,左右两端开口,在垂直于上下底面方向加磁感应强度为B的匀强磁场,在前后两个面的内侧固定有金属板作为电极,当含有大量正负离子(其重力不计)的污水充满管口从左向右流经该装置时,利用电压表所显示的两个电极间的电压U,就可测出污水流量Q(单位时间内流出的污水体积).则下列说法正确的是:ACA.后表面的电势一定高于前表面的电势,与正负哪种离子多少无关B.若污水中正负离子数相同,则前后表面的电势差为零C.流量Q越大,两个电极间的电压U越大D.污水中离子数越多,两个电极间的电压U越大61、质量为m、带电荷量为+q的小物块放在斜面上,斜面的倾角为,物块与斜面间的动摩擦因数为,设整个斜面置于磁感应强度为B的匀强磁场中,如图所示,斜面足够长,则物体向下滑动能达到的最大速度vm是多少?解:物体受力情况如答图所示,当重力的下滑分量等于摩擦力时,物体处于平衡状态,此时速度达到最大,正压力为
由二力平衡条件,可解得.62、一细棒处于磁感应强度为B的匀强磁场中,棒与磁场垂直,磁场方向水平向纸内,如图所示,棒上套一个可在其上滑动的带负电的小球C,小球质量为m,电荷量为q,球与棒间动摩擦因数为,让小球从棒上端由静止下滑,求:(1)小球的最大加速度;(2)小球的最大速度;解:(1)当带电小球开始下滑后,受到重力mg、洛伦兹力FB、绝缘棒的支承力FN和摩擦力Ff的作用,如答图所示.随着下滑速度v增大,洛伦兹力增大,棒对球的支承力FN减小,摩擦力,下滑加速度增大;当支承力FN=0时,Ff=0,加速度a达最大值,即FN=0(即Ff=0)是小球具有最大加速度的临界条件,根据这个条件可得.(2)小球达最大加速度后,虽然加速度变小,但速度还在增加,当其速度达到一定值后,棒对球的压力变为斜向下,如答图所示,随着,小球的加速度为零是小球具有最大速度的临界条件.当a=0时,,小球开始做匀速直线运动.根据平衡条件是,,,由此解得.+qm××××××××××××××××××××××××θBA63、如图,一根绝缘细杆固定在磁感应强度为B的水平匀强磁场中,杆和磁场垂直,与水平方向成θ角。杆上套一个质量为m、电量为+q的小球。小球与杆之间的动摩擦因数为μ。从A点开始由静止释放小球,使小球沿杆向下运动。设磁场区域很大,杆很长。已知重力加速度为g。求:(1)定性分析小球运动的加速度和速度的变化情况;(2)小球在运动过程中最大加速度的大小;(3)小球在运动过程中最大速度的大小。
图1Fmg解:(1)先做加速度增大的加速运动,再做加速度减小的加速运动,最后做匀速直线运动。(3分)(2)当杆对小球的弹力为零时,小球加速度最大。小球受力如图1所示FmgN图2f根据牛顿第二定律mgsinθ=ma(3分)求出a=gsinθ(2分)(3)当小球所受合力为零时,速度最大,设最大速度为vm小球受力如图2所示(2分)根据平衡条件qvmB=N+mgcosθ(2分)mgsinθ=f(2分)滑动摩擦力f=μN(1分)求出(2分)64、如图所示,真空室内存在匀强磁场,磁场方向垂直于纸面向里,磁感应强度的大小B=0.60T.磁场内有一块平面感光板ab,板一与磁场方向平行.在距ab的距离为l=16cm处,有一个点状的放射源S,它向各个方向发射粒子,粒子的速度都是.已知粒子的电荷与质量之比.现在只考虑在图纸平面中运动的粒子,求ab上被粒子打中的区域的长度.解:如答图所示,、分别为粒子的边界轨迹线.由图中几何关系得.再考虑N的右侧.任何粒子在运动中离S的距离不可能超过2R,以2R为半径、S为圆心作圆,交ab于N右侧的P2点,此即右侧能打到的最远点.由图中几何关系得.所求长度为.代入数值得.
××××××××××××abcdθOv065、如图所示,一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场,在ad边中点O,方向垂直磁场向里射入一速度方向跟ad边夹角θ=30°、大小为v0的带正电粒子,已知粒子质量为m,电量为q,ad边长为L,ab边足够长,粒子重力不计,求:(1)粒子能从ab边上射出磁场的v0大小范围.(2)如果带电粒子不受上述v0大小范围的限制,求粒子在磁场中运动的最长时间.答案:(1)<v0≤(2)解:(1)若粒子速度为v0,则qv0B=,所以有R=,设圆心在O1处对应圆弧与ab边相切,相应速度为v01,则R1+R1sinθ=,将R1=代入上式可得,v01=类似地,设圆心在O2处对应圆弧与cd边相切,相应速度为v02,则R2-R2sinθ=,将R2=代入上式可得,v02=所以粒子能从ab边上射出磁场的v0应满足<v0≤(2)由t=及T=可知,粒子在磁场中经过的弧所对的圆心角α越长,在磁场中运动的时间也越长。由图可知,在磁场中运动的半径r≤R1时,运动时间最长,弧所对圆心角为(2π-2θ),所以最长时间为t==66、如图所示,在xOy平面内有一个半径r=3cm的圆形匀强磁场区,磁感应强度B=0.2T,方向垂直于纸面向外,比荷为的正离子从坐标原点O以速度沿y方向进入磁场中.
(1)当磁场区圆心位于不同位置时正离子射出磁场时偏转角度大小也不同,求该偏转角可达到的最大值;(2)如果改变磁场区半径r,正离子射出磁场时偏转角大小也将不同,要使正离子以最大偏角飞离磁场后可穿过x轴,求r的取值范围.解:(1)正离子在磁场中做匀速圆周运动,洛伦兹力为向心力,设轨迹半径为R,则,∴.当偏转角有最大时,离子在磁场中运动的轨迹长度最大,即圆形磁场的直径为两圆的公共弦.设最大偏转角为,则.∴.(2)当,v与x轴的夹角大于0°,离子即能通过x轴,∴,.67、一带电质点,质量为m,电荷量为q,以平行于Ox轴的速度v从y轴上的A点射入图中第一象限所示的区域.为了使该质点能从x轴上的B点以垂直于Ox轴的速度v射出,可在第一象限中适当的地方加一个垂直于xOy平面、磁感应强度为B的匀强磁场.若此磁场仅分布一个圆形区域内,示这个圆形磁场区域的最小半径.(重力忽略不计)解:因为电荷有正、负两种可能性,磁场也有垂直于纸面向外和向里两种可能性,所以粒子从A到B也有两种可能的绕行方向,如答图所示.(1)当粒子沿顺时针方向绕行时,偏转有为90°,即质点在磁场中运动的轨迹为圆周的1/4,射入方向与射出方向均应与圆周(虚线所示)相切,过这两个切点M、N作入射和出射方向的垂线,其交点即为圆心(如答图甲所示).该粒子在磁场内的运动轨迹就是以为圆心、为半径的一段圆弧MN(虚线所示),在通过M、N两点所在圆周中,以MN为直径的圆周最小,所以磁场的最小半径为.(2)当粒子沿逆时针方向绕行时,偏转角为270°,如答图乙所示.因为M、N两点应位于磁场的边界上,MN弧必然在磁场内,所以最小半径就是弧MN的半径,即.因为≥,所以磁场的最小半径为
68、如图所示,在一个圆形区域内,两个方向相反且都垂直于纸面的匀强磁场分布在以直径A2A4为边界的两个半圆形区域Ⅰ、Ⅱ中,A2A4与A1A3的夹角为60°.一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A1处沿与A1A3成30°角的方向射入磁场,随后该粒子以垂直于A2A4的方向经过圆心O进Ⅱ区,最后再从A4处射出磁场.已知该粒子从射入到射出磁场所用的时间为t.求Ⅰ区和Ⅱ区中磁感应强度的大小.(忽略粒子重力)解:设粒子的入射速度为v,已知粒子带正电,故它在磁场中先顺时针做圆周运动,再逆时针做圆周运动,最后从A4点射出,用B1、B2、R1、R2、T1、T2分别表示磁场Ⅰ区和Ⅱ区中磁感应强度,轨道半径和周期,,,.设圆形区域的半径为r.如答图所示,已知带电粒子过圆心且垂直A2A4进入Ⅱ区磁场,连接A1A2,△A1OA2为等边三角形,A2为带电粒子在Ⅰ区磁场中运动轨迹的圆心,其轨道的半径.圆心角,带电粒子在Ⅰ区磁场中运动的时间为.带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA4的中点,即.在Ⅱ区磁场中运动时间为.带电粒子从射入到射出磁场所用的总时间.由以上各式得,.69、如图所示,M、N为两块带等量异种电荷的平行金属板,S1、S2为板上正对的小孔,N板右侧有两个宽度均为d的匀强磁场区域,磁感应强度大小均为B,方向分别垂直于纸面向外和向里,磁场区域右侧有一个荧光屏,取屏上与S1、S2共线的O点为原点,向上为正方向建立x轴,M板左侧电子枪发射出的热电子经小孔S1进入两板间,电子的质量为m,电荷量为e,初速度可以忽略.(1)当两板间电势差为U0时,求从小孔S2射出的电子的速度v0;(2)两金属板间电势差U在什么范围内,电子不能穿过磁场区域而打不到荧光屏上;(3)若电子能够穿过磁场区域而打到荧光屏上,在图上定性地画出电子运动的轨迹;(4)求电子打到荧光屏上的位置坐标x和金属板是电势差U的函数关系.解:(1)根据动能定理,得,
由此即可解得.(2)欲使电子不能穿过磁场区域而打不到荧光屏上,应有,而,由此即可解得.(3)电子穿过磁场区域而打到荧光屏上时运动的轨迹如答图所示.(4)若电子在磁场区域做圆周运动的轨道半径为r,穿过磁场区域打到荧光屏上的位置坐标为x,则由图中的轨迹图可得.注意到和.所以,电子打到荧光屏上的位置坐标x和金属板间电势差U的函数关系为.70、在以坐标原点O为圆心、半径为r的圆形区域内,存在磁感应强度应大小为B、方向垂直于纸面向里的匀强磁场,如图所示。一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度v沿-x方向射入磁场,它恰好从磁场边界的交点C处沿+y方向飞出。xOyCBAv (1)判断该粒子带何种电荷,并求出其比荷; (2)若磁场的方向和所在空间范围不变,而磁感应强度的大小变为B/,该粒子仍以A处相同的速度射入磁场,但飞出磁场时的速度方向相对于入射方向改变了60°角,求磁感应强度B/多大?此粒子在磁场中运动手所用时间t是多少?(1)由粒子的飞行轨迹,利用左手定则可知,该粒子带负电荷。粒子由A点射入,由C点飞出,其速度方向改变了90°,则粒子轨迹半径R=r①又qvB=m②则粒子的比荷 ③
(2)粒子从D点飞出磁场速度方向改变60°角,故AD弧所对应的圆心角为60°,粒子做国,圆周运动的半径 R/=rcot30°=r④又R/=m⑤所以 B/=B⑥粒子在磁场中飞行时间t= ⑦71、如图所示,在与的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向均垂直于纸面向里,且B1>B2.一个带负电荷的粒子从坐标原点O以速度v沿x轴负方向射出,要使该粒子经过一段时间后又经过O点,B1与B2的比值应满足什么条件?18.【解析】粒子在整个运动过程中的速度大小恒为v,交替地在xOy平面内的B1与B2磁场区域中做匀速圆周运动,轨道都是半个圆周.设粒子的质量和电荷量的大小分别为m和q,圆周运动的半径分别为r1和r2,有,①.②现分析粒子运动的轨迹,如答图所示,在xOy平面内,粒子先沿半径为r1的半圆C1运动至y轴上离O点距离为2r1的A点,接着沿半径为r2的半圆D1运动至y轴上的O1点,OO1的距离.③此后,粒子每经历一次“回旋”(即从y轴出发沿半径为r1的半圆和半径为r2的半圆回到原点下方的y轴),粒子的y坐标就减小d.设粒子经过n次回旋后与y轴交于On点,若OOn,即nd满足.④则粒子再经过半圆Cn+1就能够经过原点,式中n=1,2,3,…为回旋次数.由③、④式解得,⑤联立①、②、⑤式可得B1与B2的比值应满足的条件是
.72、如图所示,环状匀强磁场围成的中空区域,具有束缚带电粒子的作用,中空区域中的带电粒子,只要速度不是很大,都不会穿出磁场的外边界,设环状磁场的内半径R1=0.5m,外半径R2=1.0m,磁场的磁感应强度B=1.0T,若被束缚的带电粒子的比荷为,中空区域中带电粒子具有各主方向的速度.试计算(1)若粒子沿磁场区域的半径方向,平行于截面从A点射入磁场,试求粒子在磁场中运动而不穿出外边界的最大速度;(2)若粒子平行于截面从A点沿各个方向射入磁场都不能穿出磁场所在的外边界,求粒子运动的最大速度.解:(1)粒子恰不能穿出磁场时,其运动轨迹应和环状磁场外界相切,如答图所示,设其轨道半径为R,则.由洛伦兹力充当向心力,得,所以.解得.(2)沿内圆切线进入磁场的粒子最易穿出磁场区域,设其恰不穿过时速度为v,其轨迹如答图所示,其运动半径为:,依(1)讨论得.73、如图所示为两个共轴金属圆筒,轴线与纸面垂直,内筒半径为R,筒壁为网状(带电粒子可无阻挡地穿过网格).当两圆筒之间加上一定电压后,在两圆筒间的空间可形成沿半径方向的电场.内圆筒包围的空间存在一沿圆筒轴线方向的匀强磁场,磁场的磁感应强度的大小为B,方向指向纸内.一束质量为m、电荷量为q的带正电的粒子以各种不同的速率自内圆筒壁上的A点沿内圆筒半径射入磁场,现要求有的粒子的运动能满足下面三个条件:①刚刚能到达外筒的内壁而不与外筒相碰;②粒子从A点射入磁场,又从A点射出磁场;③每个粒子在磁场区域内运动所经过的总时间等于该粒子在所给磁场中做完整的圆周运动时的周期的一半.(1)为了能满足上述要求,内、外筒间电压的可能值应是多少?(2)讨论上述电压取最小值时,粒子在磁场中运动的总路程.解:(1)设带电粒子由A点沿内圆筒半径方向射入磁场时的速度用v表示,进入磁场后,在洛伦兹力作用下粒子做圆周运动,并从内筒表面上的A1点射出磁场,射出磁场时的速度大小仍为v,方向沿过A1点的内圆筒半径方向,如答图所示.粒子自A1射出磁场后便进入两圆筒间的电场中,在电场力的作用下,粒子做减速直线运动,刚到达外圆筒的内壁时,速度恰好减至零.然后粒子又在电场力作用下向A1点做加速运动,回到A1时,粒子速度增大到v,并以此速度沿内圆筒半径方向第二次进入磁场,在磁场的洛伦兹力作用下,粒子又做圆周运动,并从A2
点射出磁场.此后,粒子又再一次在电场中减速,到达外壁时调转方向加速回到A2点,从A2点进入磁场,再做圆周运动并从A3点射出磁场.这一过程多次重复到最后,粒子再次从A点射出磁场.设粒子做圆周运动的半径为r,从A点射入磁场到从A1点射出磁场经历的时间为t,绕圆心转过的角度为,为,如答图所示.有,①.②若粒子在磁场中经过n次偏转后能从A点射出磁场,应满足条件:.③根据题意有,④而,⑤解以上各式得:⑥.⑦连接图中的,由直角三角形可得:,⑧因r是粒子在洛伦兹力作用下做圆周运动的轨道半径,有,⑨由②、⑦、⑧、⑨式得到粒子射入磁场时的速度.⑩设加在两圆筒间的电压为U,由能量守恒有,把⑩式代入式得,(2)当k=1时,对应射入磁场的速度为最小,加在两圆筒间的电压亦为最小,,.由⑥式可知粒子在磁场中偏转的次数为:n=3.由⑦式可知每次偏转的角度.由⑧式和⑦式可知粒子在磁场内做圆周运动的半径.粒子在磁场内运动的总路程.
74、图中是某装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°.在A1A2左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2m.在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L.在小孔处装一个电子快门.起初快门开启,一旦有带正电微粒刚通过小孔,快门立即关闭,此后每隔开启一次并瞬间关闭.从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔.通过小孔的微粒与挡板发生碰撞而反弹,反弹速度大小是碰前的0.5倍.(1)经过一次反弹直接从小孔射出的微粒,其初速度v0应为多少?(2)求上述微粒从最初水平射入磁场到第二次离开磁场的时间.(忽略微粒所受重力影响,碰撞过程无电荷转移,已知微粒的比荷.只考虑纸面上带电微粒的运动)解:(1)如答图所示,设带正电微粒在S1S2之间任意点Q以水平速度v0进入磁场,微粒受到的洛伦兹力为F,在磁场中做圆周运动的半径为r,有:,①,②由①、②得:.欲使微粒能进入小孔,半径r的取值范围为:.③代入数据得:.欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔,还必须满足条件:.其中④由①、②、③、④可知,只有n=2满足条件,则有:.(2)设微粒在磁场中做圆周运动的周期为T0,从水平进入磁场到第二次离开磁场的总时间为t,设t1、t4分别为带电微粒第一次、第二次在磁场中运动的时间,第一次离开磁场运动到挡板的时间为t2,碰撞后再返回磁场的时间为t3,运动轨迹如答图所示,则有:
,,,,,.75、边长为100cm的正三角形光滑且绝缘的钢性框架ABC固定在光滑的水平面上,如图所示.内有垂直于框架平面B=0.5T的匀强磁场.一质量,带电荷量为小球,从BC的中点小孔P处以某一大小的速度垂直于BC边沿水平面射入磁场,设小球与框架相碰后不损失动能.求:(1)为使小球在最短的时间内从P点出来,小球的入射速度v1是多少?(2)若小球以的速度入射,则需经过多少时间才能由P点出来?解:(1)根据题意,粒子经AB、AC的中点反弹后能以最短的时间射出框架,即粒子的运动半径是0.5m.由牛顿第二定律得:,即.代入数据解得.(2)当粒子的速度为1m/s时,其半径为,其运动轨迹如答图所示.可知粒子在磁场中运动了6.5个周期.由,得,解得,故经,粒子能从P点出来.(注意:粒子在框架的角处必须要以A、B、C为圆心,这样才能保证转过角处后能够与框边垂直碰撞)76、如图(a)所示,在x≥0的区域内有如图(b)所示大小不变、方向随时间周期性变化的磁场,磁场方向垂直纸面向外时为正方向。现有一个质量为m,电量为q的带正电的粒子(不计重力),在t=0时刻从坐标原点O以速度v沿与x轴正方向成30°射入磁场,粒子运动一段时间后到达P点,此时粒子的速度与x轴正方向的夹角仍为30°。如图(a)所示(1)若B0为已知量,试求带电粒子在磁场中运动的轨道半径R和周期T0的表达式。(2)若B0不知,但已知P点的坐标为(a,0),带电粒子第一次通过x轴时就经过P点,求磁场变化周期T应满足的条件。(3)若B0不知,但已知P点的坐标为(a,0),且带电粒子通过P点的时间大于T/2,求磁感应强度B0和磁场变化周期T。解:(1)由洛化兹力提供向心力可得
∴粒子运动周期(2)由题意思知粒子运动半径R=a而=又≥∴T≥(3)∵a=(2n+1)R,n=1、2、3……xv0OPv0θy∴B0=,n=1、2、3、……又=,n=1、2、3而=∴T=.n=1、2、3、……77、在如图所示的平面直角坐标系xOy中,有一个圆形区域的匀强磁场(图中未画出),磁场方向垂直于xOy平面,O点为该圆形区域边界上的一点.现有一质量为m,带电量为+q的带电粒子(不计重力)从O点为以初速度v0沿x轴方向进入磁场,已知粒子经过y轴上P点时速度方向与+y方向夹角为θ=30º,OP=L.求:⑴磁感应强度的大小和方向;⑵该圆形磁场区域的最小面积.解:(1)由左手定则得磁场方向垂直xOy平面向里.粒子在磁场中做弧长为圆周的匀速圆周运动,如图所示,粒子在Q点飞出磁场.设其圆心为,半径为R.由几何关系有xv0OO’LPv0θyθ120°QR(L-R)sin30°=R,所以R=L. 由牛顿第二定律有,故.由以上各式得磁感应强度.
(2)设磁场区的最小面积为S.由几何关系得直径, 所以S=. 78、如图所示,直线MN下方无磁场,上方空间存在两个匀强磁场,其分界线是半径为R的半圆,两侧的磁场方向相反且垂直于纸面,磁感应强度大小都为B。现有一质量为m、电荷量为q的带负电微粒从P点沿半径方向向左侧射出,最终打到Q点,不计微粒的重力。求:(1)微粒在磁场中运动的周期;(2)从P点到Q点,微粒的运动速度大小及运动时间;(3)若向里磁场是有界的,分布在以O点为圆心、半径为R和2R的两半圆之间的区域,上述微粒仍从P点沿半径方向向左侧射出,且微粒仍能到达Q点,求其速度的最大值。NOMPQBB解:(1)由得(2)粒子的运动轨迹将磁场边界分成n等分(n=2,3,4……)由几何知识可得:;;又(1分)得(n=2,3,4……)(1分)当n为偶数时,由对称性可得(n=2,4,6……)(1分)当n为奇数时,t为周期的整数倍加上第一段的运动时间,即(n=3,5,7……)(1分)NOMPQO1哦BO21哦BBO1NOMPQO219ANOMPQO1哦BO21哦BO321哦BO4321哦BBB
(3)由几何知识得;(1分)且不超出边界须有:(1分)得(1分)O1哦BO21哦BBMPQNO当n=2时不成立,如图(1分)比较当n=3、n=4时的运动半径,知当n=3时,运动半径最大,粒子的速度最大.(2分)得:(1分)NOMPQO1哦BO21哦BO321哦BO4321哦BCC/ⅡⅠBBO1NMO21O31OPQxyAPON0h/278、如图,在x轴下方有匀强磁场,磁感应强度大小为B,方向垂直于xy平面向外,P是y轴上距原点为h的一点,N0为x轴上距原点为a的一点。A是一块平行于x轴的档板,与x轴的距离为,A的中点在y轴上,长度略小于。带电粒子与挡板碰撞前后x方向上的分速度不变,y方向上的分速度反向,大小不变。质量为m,电荷量为q(q>0)的粒子从P点瞄准N0点入射,最后又通过P点。不计重力。求粒子入射速度的所有可能值。解:设粒子的入射速度为v,第一次射出磁场的点为,与板碰撞后再次进入磁场的位置为。粒子在磁场中运动的轨道半径为R,有
…⑴,粒子速率不变,每次进入磁场与射出磁场位置间距离保持不变有…⑵,粒子射出磁场与下一次进入磁场位置间的距离始终不变,与相等.由图可以看出……⑶设粒子最终离开磁场时,与档板相碰n次(n=0、1、2、3…).若粒子能回到P点,由对称性,出射点的x坐标应为-a,即……⑷,由⑶⑷两式得……⑸若粒子与挡板发生碰撞,有……⑹联立⑶⑷⑹得n<3………⑺联立⑴⑵⑸得………⑻把代入⑻中得…………⑼…………⑾…………⑿79、如下图,在区域内存在与xy平面垂直的匀强磁场,磁感应强度的大小为B.在t=0时刻,一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与y轴正方向的夹角分布在0~180°范围内。已知沿y轴正方向发射的粒子在时刻刚好从磁场边界上点离开磁场。求:⑴粒子在磁场中做圆周运动的半径R及粒子的比荷q/m;⑵此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围;⑶从粒子发射到全部粒子离开磁场所用的时间。【答案】⑴
⑵速度与y轴的正方向的夹角范围是60°到120°⑶从粒子发射到全部离开所用时间为【解析】⑴粒子沿y轴的正方向进入磁场,从P点经过做OP的垂直平分线与x轴的交点为圆心,根据直角三角形有解得,则粒子做圆周运动的的圆心角为120°,周期为粒子做圆周运动的向心力由洛仑兹力提供,根据牛顿第二定律得,,化简得⑵仍在磁场中的粒子其圆心角一定大于120°,这样粒子角度最小时从磁场右边界穿出;角度最大时从磁场左边界穿出。角度最小时从磁场右边界穿出圆心角120°,所经过圆弧的弦与⑴中相等穿出点如图,根据弦与半径、x轴的夹角都是30°,所以此时速度与y轴的正方向的夹角是60°。角度最大时从磁场左边界穿出,半径与y轴的的夹角是60°,则此时速度与y轴的正方向的夹角是120°。所以速度与y轴的正方向的夹角范围是60°到120°⑶在磁场中运动时间最长的粒子的轨迹应该与磁场的右边界相切,在三角形中两个相等的腰为,而它的高是RRR
,半径与y轴的的夹角是30°,这种粒子的圆心角是240°。所用时间为。所以从粒子发射到全部离开所用时间为。80、如图所示,在0≤x≤a、o≤y≤范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B。坐标原点O处有一个粒子源,在某时刻发射大量质量为m、电荷量为q的带正电粒子,它们的速度大小相同,速度方向均在xy平面内,与y轴正方向的夹角分布在0~90°范围内.己知粒子在磁场中做圆周运动的半径介于到a之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一,求最后离开磁场的粒子从粒子源射出时的:(1)速度大小;(2)速度方向与y轴正方向夹角正弦。解:设粒子的发射速度为v,粒子做圆周运动的轨道半径为R,由牛顿第二定律和洛伦磁力公式,得,解得:当<R<a时,在磁场中运动时间最长的粒子,其轨迹是圆心为C的圆弧,圆弧与磁场的边界相切,如图所示,设该粒子在磁场中运动的时间为t,依题意,时,设最后离开磁场的粒子的发射方向与y轴正方向的夹角为α,由几何关系可得:再加上,解得:81、如图所示,MN、PQ是平行金属板,板长为L,两板间距离为d,PQ带正电,MN板带负电,在PQ板的上方有垂直纸面向里的匀强磁场。一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场。不计粒子重力。试求:(1)两金属板间所加电压U的大小;(2)匀强磁场的磁感应强度B的大小;
(3)在图中正确画出粒子再次进入电场中的运动轨迹,并标出粒子再次从电场中飞出的速度方向。解:(1)设带电粒子在平行金属板匀强电场中运动的时间为t,由类平抛运动可知:v0ONPQm,-qLdθθVN………………①(1分)………………②(2分)…………………③(2分)…………………④(2分)联立求解①~④式解得:……………⑤(1分)或由动能定理和运动的合成、分解的方法,联立求解得出正确的结果同样给分。设带电粒子第一次飞出电场时的速度为v即由动能定理;;和①③④联立可得(2)带电粒子以速度v飞出电场后射入匀强磁场做匀速圆周运动,由…………………………………………………………………⑥(2分)…………………………………………………………………⑦(1分)…………………………………………………………………⑧(1分)………………………………………………………………………⑨(1分)联立求解①③④⑤⑥⑦⑧⑨可得……………………………⑩(1分)或由下列常规方法求解:…………………………………………⑴(1分)……………………………………………………………⑵(1分)……………………………………………………………⑶(1分)
……………………………………………………………⑷(1分)……………………………………………………………⑸(1分)APyxBEQθOv联立以上有关方程求解可得:…………………⑹(1分)82、如图所示,一对平行金属板水平放置,板间距离为d,板间有磁感应强度为B的垂直于纸面向里的匀强磁场,将金属板接入如图所示的电路,已知电源的内电阻为r,滑动变阻器的总电阻为R,现将开关K闭合,并将滑动触头P调节至距离电阻R的右端为其总长度的1/4时,让一个质量为m、电量为q宏观带电粒子从两板间的正中央以某一初速度水平飞入场区,发现其恰好能够做匀速圆周运动。(1)试判断该粒子的电性,求电源的电动势;(2)若将滑动触头P调到电阻R的正中间位置时,该粒子仍以同样的状态入射,发现其沿水平方向的直线从板间飞出,求该粒子进入场区时的初速度;(3)若将滑块触头P调到最左边,该粒子仍以同样的状态入射,发现其恰好从金属板的边缘飞出,求粒子飞出时的动能。(1)负电…………………………………………………………………(2分)∵mg=ε×……………………………………………(2分)∴ε=4(r+R)dmg/Rq………………………………………………(2分)(2)mg+qv0B=12RR+rε×qd………………………………………………(4分)∴v0=mg/qB………………………………………………………………(2分)(3)Ek=mv20+3mg×=mgd+…………………………………(6分)QAPyxαθvvO1MONβ83、如图所示,直角坐标系在一真空区域里,y轴的左方有一匀强电场,场强方向跟y轴负方向成θ=30º角,y轴右方有一垂直于坐标系平面的匀强磁场,在x轴上的A点有一质子发射器,它向x轴的正方向发射速度大小为v=2.0×106m/s的质子,
质子经磁场在y轴的P点射出磁场,射出方向恰垂直于电场的方向,质子在电场中经过一段时间,运动到x轴的Q点。已知A点与原点O的距离为10cm,Q点与原点O的距离为(20-10)cm,质子的比荷为。求:(1)磁感应强度的大小和方向;(2)质子在磁场中运动的时间;(3)电场强度的大小。解答:(1)设质子在磁场中做圆运动的半径为r。过A、P点作速度v的垂线,交点即为质子在磁场中作圆周运动的圆心O1。由几何关系得α=θ=30º,所以:r=2OA=20cm。(2分)设磁感应强度为B,根据质子的运动方向和左手定则,可判断磁感应强度的方向为垂直于纸面向里。(2分)根据:(2分)(2)设质子在磁场中运动的时间为t,如图所示,质子在磁场中转过的圆周角为,设质子在磁场中运动的周期为Ts(6分)(3)如图所示,过Q点做平行于P点速度方向的平行线,交AM于N点,在三角形QAN中,边长QA=。由几何关系可知β=θ=30º,AN=20cm,所以,N点与O1点是重合的。质子在平行于电场方向上做匀速直线运动,在垂直于电场方向做匀加速直线运动,由几何关系得:(4分)(4分)
图84、如图所示的坐标系,x轴沿水平方向,y轴沿竖直方向。在x轴上方空间的第一、第二象限内,既无电场也无磁场,在第三象限,存在沿y轴正方向的匀强电场和垂直xy平面(纸面)向里的匀强磁场,在第四象限,存在沿y轴负方向、场强大小与第三象限电场场强相等的匀强电场。一质量为m、电荷量为q的带电质点,从y轴上y=h处的P1点以一定的水平初速度沿x轴负方向进入第二象限。然后经过x轴上x=–2h处的P2点进入第三象限,带电质点恰好能做匀速圆周运动。之后经过y轴上y=–2h处的P3点进入第四象限。已知重力加速度为g。求:(1)粒子到达P2点时速度的大小和方向;(2)第三象限空间中电场强度和磁感应强度的大小;(3)带电质点在第四象限空间运动过程中最小速度的大小和方向。解:(1)参见图,带电质点从P1到P2,由平抛运动规律图h=…………①(2分)v0=…………………②(1分)vy=gt……………………③(1分)求出v=…④(2分)方向与x轴负方向成45°角(1分)用其它方法求出正确答案的同样给分。(2)带电质点从P2到P3,重力与电场力平衡,洛伦兹力提供向心力Eq=mg………………………………⑤(1分)Bqv=m…………………………⑥(2分)(2R)2=(2h)2+(2h)2………………⑦(2分)由⑤解得E=…………………………………(2分)联立④⑥⑦式得B=……………………………………(2分)(3)带电质点进入第四象限,水平方向做匀速直线运动,竖直方向做匀减速直线运动。当竖直方向的速度减小到0,此时质点速度最小,即v在水平方向的分量vmin=vcos45°=………………………………(2分)
方向沿x轴正方向…………………………………………(2分)85、电子自静止开始经M、N板间(两板间的电压为U)的电场加速后从A点垂直于磁场边界射入宽度为d的匀强磁场中,电子离开磁场时的位置P偏离入射方向的距离为L,如图所示.求:(1)正确画出电子由静止开始直至离开匀强磁场时的轨迹图;(用尺和圆规规范作图)(2)匀强磁场的磁感应强度.(已知电子的质量为m,电荷量为e)17.(12分)分析和解:(1)作电子经电场和磁场中的轨迹图,如右图所示(作图2分)(2)设电子在M、N两板间经电场加速后获得的速度为v,由动能定理得:…………………………………………①(2分)电子进入磁场后做匀速圆周运动,设其半径为r,则:………………………………②(3分)由几何关系得:……………………③(2分)联立求解①②③式得:…………………(3分)Bxy0-lv0E86、如图所示,坐标空间中有场强为E的匀强电场和磁感应强度为B的匀强磁场,Y轴为两种场的分界面,图中虚线为磁场区域的右边界,现有一质量为m,电荷量为-q的带电粒子从电场中坐标位置(-l,0)处,以初速度v0沿x轴正方向开始运动,且已知l=(重力不计),试求:使带电粒子能穿越磁场区域而不再返回电场中,磁场的宽度d应满足的条件.解:带电粒子在电场中做类平抛运动,设运动的加速度为a.由牛顿运动定律得:qE=ma设粒子出电场、入磁场时速度的大小为v,此时在Y轴方向的分速度为vy
,粒子在电场中运动的时间为t.则有:vy=atl=v0t解得:vy=v0v==v0(4分)设v的方向与y轴夹角为θ,则有cosθ==得θ=450.(3分)粒子进入磁场后在洛伦兹力作用下做圆周运动,如图所示,θvθR则有:qvB=可得:R=(4分)由图中几何关系可知,要使粒子穿越磁场区域,磁场的宽度应满足的条件d<R(1+cosθ)结合已知条件解以上各式可得:d<(4分)v0M图20NLhab87、如图20所示,地面上方竖直界面N左侧空间存在着水平的、垂直纸面向里的匀强磁场,磁感应强度B=2.0T。与N平行的竖直界面M左侧存在竖直向下的匀强电场,电场强度E1=100N/C。在界面M与N之间还同时存在着水平向左的匀强电场,电场强度E2=100N/C。在紧靠界面M处有一个固定在水平地面上的竖直绝缘支架,支架上表面光滑,支架上放有质量m2=1.8×10-4kg的带正电的小物体b(可视为质点),电荷量q2=1.0×10-5C。一个质量为m1=1.8×10-4kg,电荷量为q1=3.0×10-5C的带负电小物体(可视为质点)a以水平速度v0射入场区,沿直线运动并与小物体b相碰,a、b两个小物体碰后粘合在一起成小物体c,进入界面M右侧的场区,并从场区右边界N射出,落到地面上的Q点(图中未画出)。已知支架顶端距地面的高度h=1.0m,M和N两个界面的距离L=0.10m,g取10m/s2。求:(1)小球a水平运动的速率。(2)物体c刚进入M右侧的场区时的加速度。(3)物体c落到Q点时的速率。(1)a向b运动过程中受向下的重力,向上的电场力和向下的洛仑兹力。小球a的直线运动必为匀速直线运动,a受力平衡,因此有q1E1-q1v0B-m1g=0解得v0=20m/s…………3分(2)二球相碰动量守恒,解得…………1分物体c所受洛仑兹力,方向向下…………1分物体c在M有场区受电场力F2=(q1-q2)E2=4×10-3N,方向向右
物体c受到的重力G=(m1+m2)g=3.6×10-3N,方向向下物体c受到的合力F合=物体c的加速度a=m/s2…………1分设合力的方向与水平方向的夹角为θ,则tanθ==1,解得θ=45º,加速度指向右下方与水平方向成45º角。…………1分(3)物体c通过界面M后的飞行过程中电场力和重力都对它做正功。设物体c落到Q点时的速率为,由动能定理(m1+m2)gh+(q1-q2)E2L=…………1分解得vt=m/s…………1分88、如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C,方向与金箔成37°角。紧挨边界ab放一点状粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的粒子,已知:m0=6.64×10-27kg,q0=3.2×10-19C,初速率v=3.2×106m/s。(sin37°=0.6,cos37°=0.8)求:(1)粒子在磁场中作圆周运动的轨道半径R;(2)金箔cd被粒子射中区域的长度L;(3)设打在金箔上d端离cd中心最远的粒子沿直线穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN=40cm,则此粒子从金箔上穿出时,损失的动能为多少?解:(1)粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即(2分)则(2分)(2)设cd中心为O,向c端偏转的粒子,当圆周轨迹与cd相切时偏离O最远,设切点为P,对应圆心O1,如图所示,则由几何关系得:
(3分)向d端偏转的粒子,当沿Sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得:(3分)故金箔cd被粒子射中区域的长度L=(1分)(3)设从Q点穿出的粒子的速度为,因半径O2Q∥场强E,则⊥E,故穿出的粒子在电场中做类平抛运动,轨迹如图所示。(1分)沿速度方向做匀速直线运动,位移,(1分)沿场强E方向做匀加速直线运动,位移,(1分)89、如图所示,x轴上方存在磁感应强度为B的圆形匀强磁场区域,磁场方向垂直纸面向外(图中未画出)。x轴下方存在匀强电场,场强大小为E,方向沿与x轴负方向成60°角斜向下。一个质量为m,带电量为+e的质子以速度v0从O点沿y轴正方向射入匀强磁场区域。质子飞出磁场区域后,从b点处穿过x轴进入匀强电场中,速度方向与x轴正方向成30°,之后通过了b点正下方的c点。不计质子的重力。(1)画出质子运动的轨迹,并求出圆形匀强磁场区域的最小半径和最小面积;(2)求出O点到c点的距离。解(1)质子先在匀强磁场中做匀速圆周运动,射出磁场后做匀速直线运动,最后进入匀强电场做类平抛运动,轨迹如图所示.图2分根据牛顿第二定律,有 (2分)要使磁场的区域面积最小,则Oa为磁场区域的直径,由几何关系可知:
求出圆形匀强磁场区域的最小半径 ( 1分)圆形匀强磁场区域的最小面积为(2分)(2)质子进入电场后,做类平抛运动,垂直电场方向:;(2分)平行电场方向:,(2分)由牛顿第二定律,(1分) 解得:。(2分)O点到c点的距离:(2分)xyAOMNθv090、如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应为B,方向垂直xOy平面向里,电场线平行于y轴。一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴的方向夹角为。不计空气阻力,重力加速度为g,求(1)电场强度E的大小和方向;(2)小球从A点抛出时初速度v0的大小;(3)A点到x轴的高度h.答案:(1),方向竖直向上(2)(3)【解析】本题考查平抛运动和带电小球在复合场中的运动。(1)小球在电场、磁场中恰能做匀速圆周运动,说明电场力和重力平衡(恒力不能充当圆周运动的向心力),有①
②xyAOMNθv0θO/P重力的方向竖直向下,电场力方向只能向上,由于小球带正电,所以电场强度方向竖直向上。(2)小球做匀速圆周运动,O′为圆心,MN为弦长,,如图所示。设半径为r,由几何关系知③小球做匀速圆周运动的向心力由洛仑兹力白日提供,设小球做圆周运动的速率为v,有④由速度的合成与分解知⑤由③④⑤式得⑥(3)设小球到M点时的竖直分速度为vy,它与水平分速度的关系为百度文库-让每个人平等地提升自我⑦由匀变速直线运动规律⑧由⑥⑦⑧式得⑨dvl1l2BEPQ91、如图,在宽度分别为l1和l2的两个毗邻的条形区域分别有匀强磁场和匀强电磁场,磁场方向垂直于纸面向里,电场方向与电、磁场匀界线平行左右。一带正电荷的粒子以速率v从磁场区域上边界的P点斜射入磁场,然后以垂直于电、磁场分界线的方向进入电场,最后从电场边界上的Q点射出,已知PQ垂直于电场方向,粒子轨迹与电、磁场分界线的交点到PQ的距离为d。不计重力,求电场强度与磁感应强度大小之比及粒子在磁场与电场中运动时间之比。dvl1BPP/OR答案【解析】粒子在磁场中做匀速圆周运动,如图所示。由于粒子在分界线处的速度与分界线垂直。圆心O应在分界线上,OP长度即为粒子运动的圆弧的半径R.由几何关系得
………①设粒子的质量和所带正电荷分别为m和q,由洛仑兹力公式和牛顿第二定律得……………②设为虚线与分界线的交点,,则粒子在磁场中的运动时间为……③式中有………④粒子进入电场后做类平抛运动,其初速度为v,方向垂直于电场.设粒子的加速度大小为a,由牛顿第二定律得…………⑤由运动学公式有……⑥………⑦由①②⑤⑥⑦式得…………⑧由①③④⑦式得92、图中左边有一对平行金属板,两板相距为d,电压为V;两板之间有匀强磁场,磁场应强度大小为B0,方向平行于板面并垂直于纸面朝里。图中右边有一边长为a的正三角形区域EFG(EF边与金属板垂直),在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行于金属板面,垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力(1)已知这些离子中的离子甲到达磁场边界EG后,从边界EF穿出磁场,求离子甲的质量。(2)已知这些离子中的离子乙从EG边上的I点(图中未画出)穿出磁场,且GI长为,求离子乙的质量。(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上什么区域内可能有离子到达。解析:(1)在粒子进入正交的电磁场做匀速直线运动,设粒子的速度为v,电场的场强为E0,根据平衡条件得①
②由①②化简得③粒子甲垂直边界EF进入磁场,又垂直边界EF穿出磁场,则轨迹圆心在EF上。粒子运动中经过EG,说明圆轨迹与EG相切,在如图的三角形中半径为R=acos30°tan15°④tan15°=⑤联立④⑤化简得⑥在磁场中粒子所需向心力由洛伦磁力提供,根据牛顿第二定律得⑦联立③⑦化简得⑧(2)由于1点将EG边按1比3等分,根据三角形的性质说明此轨迹的弦与EG垂直,在如图的三角形中,有
⑨同理(10)(3)最轻离子的质量是甲的一半,根据半径公式离子的轨迹半径与离子质量呈正比,所以质量在甲和最轻离子之间的所有离子都垂直边界EF穿出磁场,甲最远离H的距离为,最轻离子最近离H的距离为,所以在离H的距离为到之间的EF边界上有离子穿出磁场。比甲质量大的离子都从EG穿出磁场,期中甲运动中经过EG上的点最近,质量最大的乙穿出磁场的1位置是最远点,所以在EG上穿出磁场的粒子都在这两点之间。93、右图中左边有一对平行金属板,两板相距为d.电压为V;两板之间有匀强磁场,磁感应强度大小为,方向与金属板面平行并垂直于纸面朝里。图中右边有一半径为R、圆心为O的圆形区域内也存在匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。一电荷量为q的正离子沿平行于全属板面、垂直于磁场的方向射入平行金属板之间,沿同一方向射出平行金属板之间的区域,并沿直径EF方向射入磁场区域,最后从圆形区城边界上的G点射出.已知弧所对应的圆心角为,不计重力.求(1)离子速度的大小;
(2)离子的质量.答案:(1)(2)解析:(1)由题设知,离子在平行金属板之间做匀速直线运动,安所受到的向上的压力和向下的电场力平衡①式中,是离子运动速度的大小,是平行金属板之间的匀强电场的强度,有②由①②式得③(2)在圆形磁场区域,离子做匀速圆周运动,由洛伦兹力公式和牛顿第二定律有④式中,和分别是离子的质量和它做圆周运动的半径。由题设,离子从磁场边界上的点G穿出,离子运动的圆周的圆心必在过E点垂直于EF的直线上,且在EG的垂直一平分线上(见右图)。由几何关系有⑤式中,是与直径EF的夹角,由几何关系得⑥联立③④⑤⑥式得,离子的质量为⑦
94、如图,在xoy平面内,MN和x轴之间有平行于y轴的匀强电场和垂直于xoy平面的匀强磁场.y轴上离坐标原点4L的A点处有一电子枪,可以沿+x方向射出速度为v0的电子(质量为m,电量为e).如果电场和磁场同时存在,电子将做匀速直线运动.如果撤去电场,只保留磁场,电子将从x轴上距坐标原点3L的C点离开磁场.不计重力的影响.求:xyoL2L3L4L2L4L6LNMv0AC(1)磁感应强度B和电场强度E的大小和方向;(2)如果撤去磁场,只保留电场,电子将从D点(图中未标出)离开电场.求D点的坐标;(3)电子通过D点时的动能.解:(1)只有磁场时,电子运动轨迹如图1所示 (1分) 洛仑兹力提供向心力 (1分) 由几何关系 R2=(3L)2+(4L-R)2(2分)求出 垂直纸面向里 (2分) 电子做匀速直线运动 Ee=Bev0(1分)xyoL2L3L4L2L4L6LDv0A图2xyoL2L3L4L2L4L6Lv0A图1vDMNNM求出 沿y轴负方向 (2分)(2)只有电场时,电子从MN上的D点离开电场,如图2所示(1分) 设D点横坐标为x x=v0t(1分) (1分)求出D点的横坐标为 (1分)
纵坐标为y=6L(1分)(3)从A点到D点,由动能定理 (2分) 求出 (2分)95、如图1所示,宽度为的竖直狭长区域内(边界为),存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场(如图2所示),电场强度的大小为,表示电场方向竖直向上。时,一带正电、质量为的微粒从左边界上的点以水平速度射入该区域,沿直线运动到点后,做一次完整的圆周运动,再沿直线运动到右边界上的点。为线段的中点,重力加速度为g。上述、、、、为已知量。(1)求微粒所带电荷量和磁感应强度的大小;(2)求电场变化的周期;(3)改变宽度,使微粒仍能按上述运动过程通过相应宽度的区域,求的最小值。解析:(1)微粒作直线运动,则①微粒作圆周运动,则②联立①②得
③④(2)设粒子从N1运动到Q的时间为t1,作圆周运动的周期为t2,则⑤⑥⑦联立③④⑤⑥⑦得⑧电场变化的周期⑨(3)若粒子能完成题述的运动过程,要求d≥2R(10)联立③④⑥得(11)设N1Q段直线运动的最短时间为tmin,由⑤(10)(11)得因t2不变,T的最小值96、如图甲,A、B两板间距为,板间电势差为U,C、D两板间距离和板长均为L,两板间加一如图乙所示的电压.在S处有一电量为q、质量为m的带电粒子,经A、B间电场加速又经C、D间电场偏转后进入一个垂直纸面向里的匀强磁场区域,磁感强度为B
.不计重力影响,欲使该带电粒子经过某路径后能返回S处.求:(1)匀强磁场的宽度L′至少为多少?(2)该带电粒子周期性运动的周期T.解:(1)AB加速阶段,由动能定理得:偏转阶段,带电粒子作类平抛运动偏转时间侧移量设在偏转电场中,偏转角为θ则即θ=由几何关系:Rcos45°+R=L′Rsin45°=∴L′=注:L′也可由下面方法求得:粒子从S点射入到出偏转电场,电场力共做功为W=2qU设出电场时速度为v′,有∴v′=
粒子在磁场中做圆周运动的半径:∴(2)设粒子在加速电场中运动的时间为t2则t2=带电粒子在磁场中做圆周运动的周期实际转过的角度α=2π-2θ=在磁场中运动时间t3=故粒子运动的周期T=2t2+2t1+t3=4L97、如图甲所示,在两平行金属板的中线OO′某处放置一个粒子源,粒子源沿OO′方向连续不断地放出速度v0=1.0×105m/s的带正电的粒子.在直线MN的右侧分布范围足够大的匀强磁场,磁感应强度B=0.01πT,方向垂直纸面向里,MN与中线OO′垂直.两平行金属板的电压U随时间变化的U-t图线如图乙所示.已知带电粒子的荷质比,粒子的重力和粒子之间的作用力均可忽略不计,若t=0.1s时刻粒子源放出的粒子恰能从平行金属板边缘离开电场(设在每个粒子通过电场区域的时间内,可以把板间的电场看作是恒定的).求:(1)在t=0.1s时刻粒子源放出的粒子离开电场时的速度大小和方向.(2)从粒子源放出的粒子在磁场中运动的最短时间和最长时间.图乙1000.10t/sU/VVV0.20.30.4OMN图甲O′解:⑴设板间距为d,t=0.1s时刻释放的粒子在板间做类平抛运动在沿电场方向上
粒子离开电场时,沿电场方向的分速度粒子离开电场时的速度粒子在电场中的偏转角为θ得θ=450⑵带电粒在匀强磁场中做匀速圆周运动的周期不同时刻释放的粒子在电场中的偏转角θ不同,进入磁场后在磁场中运动的时间不同,θ大的在磁场中的偏转角大,运动时间长.t=0时刻释放的粒子,在电场中的偏转角为0,在磁场中运动的时间最短:t=0.1s时刻释放的粒子,在电场中的偏转角最大为450,在磁场中运动的时间最长:98、电子扩束装置由电子加速器、偏转电场和偏转磁场组成.偏转电场由加了电压的相距为d的两块水平平行放置的导体板形成,匀强磁场的左边界与偏转电场的右边界相距为s,如图甲所示.大量电子(其重力不计)由静止开始,经加速电场加速后,连续不断地沿平行板的方向从两板正中间射入偏转电场.当两板不带电时,这些电子通过两板之间的时间为2t0,当在两板间加如图乙所示的周期为2t0、幅值恒为U0的电压时,所有电子均从两板间通过,进入水平宽度为l,竖直宽度足够大的匀强磁场中,最后通过匀强磁场打在竖直放置的荧光屏上.问:⑴电子在刚穿出两板之间时的最大侧向位移与最小侧向位移之比为多少?⑵要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多少?4t0t03t02t0t0U0U乙lB荧光屏U++--甲e→⑶在满足第(2)问的情况下,打在荧光屏上的电子束的宽度为多少?(已知电子的质量为m、电荷量为e)解⑴由题意可知,要使电子的侧向位移最大,应让电子从0、2t0、4t0
……等时刻进入偏转电场,在这种情况下,电子的侧向位移为 要使电子的侧向位移最小,应让电子从t0、3t0……等时刻进入偏转电场,在这种情况下,电子的侧向位移为所以最大侧向位移和最小侧向位移之比为⑵设电子从偏转电场中射出时的偏向角为q,由于电子要垂直打在荧光屏上,所以电子在磁场中运动半径应为:设电子从偏转电场中出来时的速度为vt,垂直偏转极板的速度为vy,则电子从偏转电场中出来时的偏向角为:式中又由上述四式可得:⑶(由于各个时刻从偏转电场中出来的电子的速度大小相同,方向也相同,因此电子进入磁场后的半径也相同. 由第(1)问可知电子从偏转电场中出来时的最大侧向位移和最小侧向位移的差值为:所以打在荧光屏上的电子束的宽度为99、如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴向右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子。在0~3t0时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t=0时刻进入两板间的带电粒子恰好在t0时刻经极板边缘射入磁场。上述m、q、l、l0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)(1)求电压U的大小。(2)求t0时进入两板间的带电粒子在磁场中做圆周运动的半径。(3)何时进入两板间的带电粒子在磁场中的运动时间最短?求此最短时间。图甲
图乙答案:(1)(2)(3)【解析】(1)t=o时刻进入两极板的带电粒子在电场中做匀变速曲线运动,t0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为l/2,则有①Eq=ma②l/2=at02/2③联立以上三式,解得两极板间偏转电压为④。(2)t0/2时刻进入两极板的带电粒子,前t0/2时间在电场中偏转,后t0/2时间两极板没有电场,带电粒子做匀速直线运动。带电粒子沿x轴方向的分速度大小为v0=l/t0⑤带电粒子离开电场时沿y轴负方向的分速度大小为⑥带电粒子离开电场时的速度大小为⑦设带电粒子离开电场进入磁场做匀速圆周运动的半径为R,则有⑧联立③⑤⑥⑦⑧式解得⑨。(3)2t0时刻进入两极板的带电粒子在磁场中运动时间最短。带电粒子离开磁场时沿y轴正方向的分速度为⑩,设带电粒子离开电场时速度方向与y轴正方向的夹角为,则,
联立③⑤⑩式解得,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为,所求最短时间为,带电粒子在磁场中运动的周期为,联立以上两式解得。【考点】带电粒子在匀强电场、匀强磁场中的运动100、如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里。位于极板左侧的粒子源沿x轴间右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子在0~3t时间内两板间加上如图乙所示的电压(不考虑极边缘的影响)。已知t=0时刻进入两板间的带电粒子恰好在t0时,刻经极板边缘射入磁场。上述m、q、l、l0、B为已知量。(不考虑粒子间相互影响及返回板间的情况)(1)求电压U的大小。(2)求时进入两板间的带电粒子在磁场中做圆周运动的半径。(3)何时把两板间的带电粒子在磁场中的运动时间最短?求此最短时间。图甲图乙答案:(1)(2)(3)【解析】(1)t=o时刻进入两极板的带电粒子在电场中做匀变速曲线运动,t0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为l/2,则有①
BxyOQPllv0●α2αEq=ma②l/2=at02/2③联立以上三式,解得两极板间偏转电压为④。(2)t0/2时刻进入两极板的带电粒子,前t0/2时间在电场中偏转,后t0/2时间两极板没有电场,带电粒子做匀速直线运动。带电粒子沿x轴方向的分速度大小为v0=l/t0⑤带电粒子离开电场时沿y轴负方向的分速度大小为⑥带电粒子离开电场时的速度大小为⑦设带电粒子离开电场进入磁场做匀速圆周运动的半径为R,则有⑧联立③⑤⑥⑦⑧式解得⑨。(3)2t0时刻进入两极板的带电粒子在磁场中运动时间最短。带电粒子离开磁场时沿y轴正方向的分速度为⑩,设带电粒子离开电场时速度方向与y轴正方向的夹角为,则,联立③⑤⑩式解得,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为,所求最短时间为,带电粒子在磁场中运动的周期为,联立以上两式解得。