金华十校高考模拟考试数学卷定稿
2017年金华十校高考模拟考试
数学试题卷
本试卷分第Ⅰ卷和第Ⅱ卷两部分.考试时间120分钟. 试卷总分为150分。请考生按规定用笔将所用试题的答案涂、写在答题纸上.
参考公式:
如果事件A、B互斥,那么 柱体的体积公式
P(A+B)= P(A)+ P(B) V=Sh
如果事件A、B相互独立,那么 其中S表示柱体的底面积,h表示柱体的高
P(A•B)= P(A)•P(B) 锥体的体积公式
如果事件A在一次试验中发生的概率为p,那么n V=Sh
次独立重复试验中事件A恰好发生k次的概率 其中S表示锥体的底面积,h表示锥体的高.
Pn(k)= 球的表面积公式
台体的体积公式 S=4πR2
V=(S1++S2) h 球的体积公式
其中S1、S2表示台体的上、下底面积,h表示棱 V=πR3
台的高. 其中R表示球的半径
选择题部分(共40分)
一、选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1. 已知i为虚数单位,则
A. B. C. D.3
2.已知,,则为
A. B. C. D.
3.若,则
A.56 B.-56 C.35 D.-35
4.设函数f(x)=sin(wx+j)(w >0),则f(x)的奇偶性
A.与w有关,且与j有关 B.与w有关,但与j无关
C.与w无关,且与j无关 D.与w无关,但与j有关
5. 已知,则是的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6. 在△ABC中,角A,B,C的对边分别为a,b,c,已知∠B =30º,△ABC的面积为.且
sinA+sinC=2sinB,则b的值为
A. B. C. D.
7. 将5名同学分到甲、乙、丙3个小组,若甲组至少两人,乙、丙组每组至少一人,则不同的
分配方案的种数为
A.50 B.80 C.120 D.140
8. 已知a,b为实常数,{ci}(i∈N*)是公比不为1的等比数列,直线ax+by+ci=0与抛物线y2=2px(p>0)
均相交,所成弦的中点为Mi(xi,yi),则下列说法错误的是
A.数列{xi}可能是等比数列 B.数列{yi}是常数列
C. 数列{xi}可能是等差数列 D.数列{xi+yi }可能是等比数列
9. 若定义在(0,1)上的函数f(x)满足:f(x)>0且对任意的x∈(0,1),有,则
A. 对任意的正数M,存在x∈(0,1),使f(x)≥M
(第10题图)
B1
A1
D1
C1
A
C
B
D
P
M
N
B. 存在正数M,对任意的x∈(0,1),使f(x)≤M
C. 对任意的x1,x2∈(0,1)且x1
f(x2)
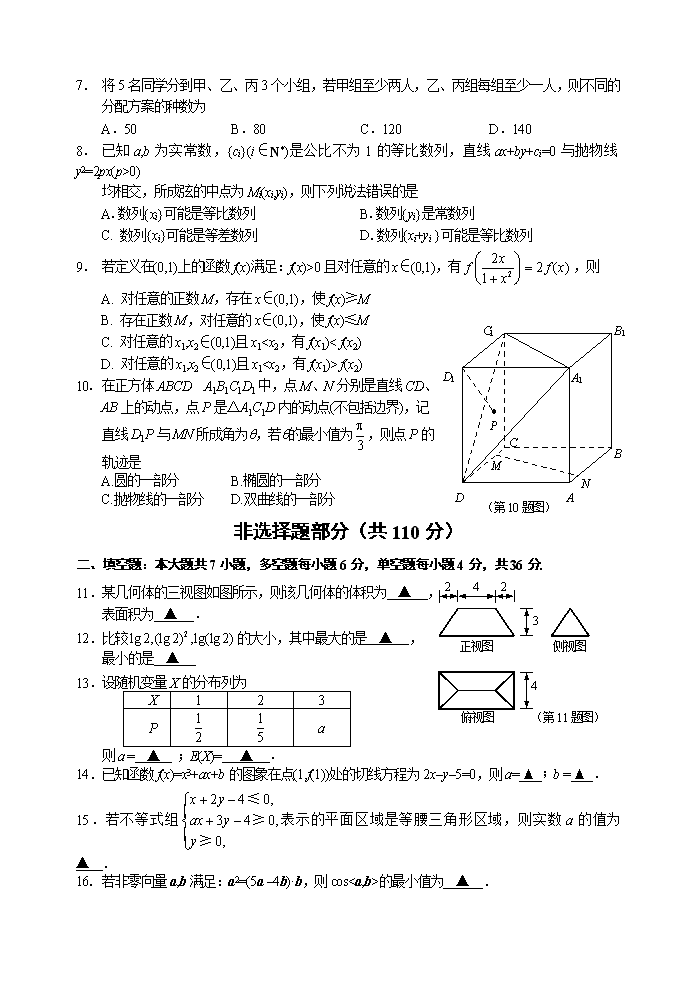
10. 在正方体ABCD-A1B1C1D1中,点M、N分别是直线CD、
AB上的动点,点P是△A1C1D内的动点(不包括边界),记
直线D1P与MN所成角为q,若q的最小值为,则点P的
轨迹是
A.圆的一部分 B.椭圆的一部分
C.抛物线的一部分 D.双曲线的一部分
非选择题部分(共110分)
(第11题图)
正视图
俯视图
侧视图
2
4
2
3
4
二、填空题:本大题共7小题,多空题每小题6分,单空题每小题4分,共36分.
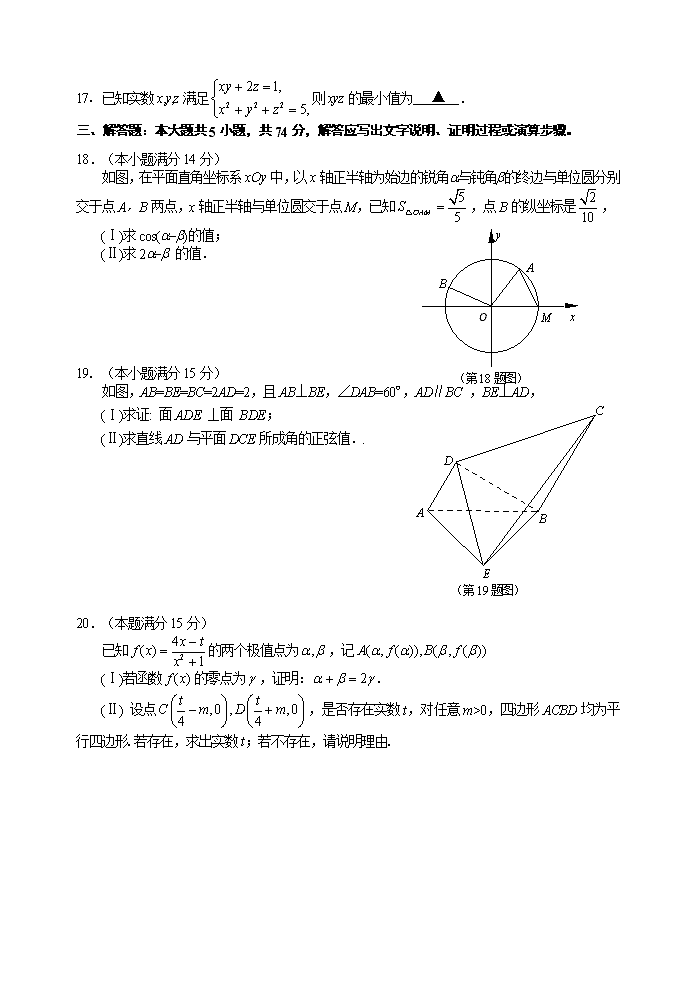
11.某几何体的三视图如图所示,则该几何体的体积为 ▲ ,
表面积为 ▲ .
12.比较的大小,其中最大的是 ▲ ,
最小的是 ▲
13.设随机变量X的分布列为
X
1
2
3
P
a
则a = ▲ ;E(X)= ▲ .
14.已知函数f(x)=x3+ax+b的图象在点(1,f(1))处的切线方程为2x-y-5=0,则a= ▲ ;b = ▲ .
15.若不等式组表示的平面区域是等腰三角形区域,则实数a的值为 ▲ .
16. 若非零向量a,b满足:a2=(5a -4b)·b,则cos的最小值为 ▲ .
17. 已知实数x,y,z满足则xyz的最小值为 ▲ .
三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤。
18.(本小题满分14分)
(第18题图)
O
x
y
A
B
M
如图,在平面直角坐标系xOy中,以x轴正半轴为始边的锐角a与钝角b的终边与单位圆分别交于点A,B两点,x轴正半轴与单位圆交于点M,已知,点B的纵坐标是,
(Ⅰ)求cos(a-b)的值;
(Ⅱ)求2a-b 的值.
19. (本小题满分15分)
E
D
A
B
C
(第19题图)
如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60º,AD∥BC ,BE⊥AD,
(Ⅰ)求证: 面ADE ⊥面 BDE;
(Ⅱ)求直线AD与平面DCE所成角的正弦值..
20.(本题满分15分)
已知的两个极值点为,记
(Ⅰ)若函数的零点为,证明:.
(Ⅱ) 设点,是否存在实数t,对任意m>0,四边形ACBD均为平行四边形.若存在,求出实数t;若不存在,请说明理由.
21.(本小题满分15分)
A
B
C
P
F
Q
O
x
y
(第20题图)
已知椭圆M:的右焦点F的坐标为(1,0),P,Q为椭圆上位于轴右侧的两个动点,使PF⊥QF,C为PQ中点,线段PQ的垂直平分线交x轴,y轴于点(线段PQ不垂直x轴),当Q运动到椭圆的右顶点时,.
(Ⅰ)求椭圆M的标准方程;
(Ⅱ)若,求直线PQ的方程.
22. (本小题满分15分)
已知数列{an}满足, ,
(Ⅰ) 证明: ;
(Ⅱ) 证明:.
2017年金华十校高考模拟考试
数学卷评分标准与参考答案
一、选择题(5×8=40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
D
B
D
A
D
B
C
A
B
二、填空题(多空题每题6分,单空题每题4分,共36分)
11. 40,; 12.; 13.; 14.-1,-3
15.4; 16. 17.
三. 解答题(74分)
18.解:(Ⅰ)由和为锐角,∴
又点B的纵坐标是,∴
∴
(Ⅱ)∵,
,∴
∵,∴
∵
故
19.解:(Ⅰ)∵AB= 2AD,∠DAB=60º,∴AD⊥DB,
又BE⊥AD,且BD∩BE={B},
∴AD⊥面BDE,又AD Ì面ADE,∴面ADE ⊥面 BDE;
(Ⅱ)∵BE⊥AD,AB⊥BE ,∴BE⊥面ABCD,
∴点E到面的距离就是线段BE的长为2,
设与平面所成角为,点到面的距离为,
由得:,可解得,
而,则,
故直线与平面所成角的正弦值为.
20. 解:(Ⅰ)
即
∴
,即,则零点
∴得证.
(Ⅱ) 要使构成平行四边形,
由得,只需
∴
所以
21.解:(Ⅰ) 当运动到椭圆的右顶点时,轴,∴,
又,∴
椭圆M的标准方程为:
(Ⅱ)设直线的方程为,显然,联立椭圆方程得:
,设点,
由韦达定理:
由得:3b2-1+4kb=0 (4)
点,
∴线段的中垂线AB方程:
令可得:,则A为BC中点,
故,
由(4)式得:,则
,得:
∴或,
经检验,满足条件(1)(2)(3) ,
故直线PQ的方程为:或.
22. 解:(Ⅰ) 证明:∵①,∴②
由②①得:,
∴
(Ⅱ) 证明:由(Ⅰ)得:
∴
令,则③
∴④
由,,易得
由③-④得:
∴,,得
根据得:,∴
∴
一方面:
另一方面:由可知: