- 2021-05-14 发布 |
- 37.5 KB |
- 8页

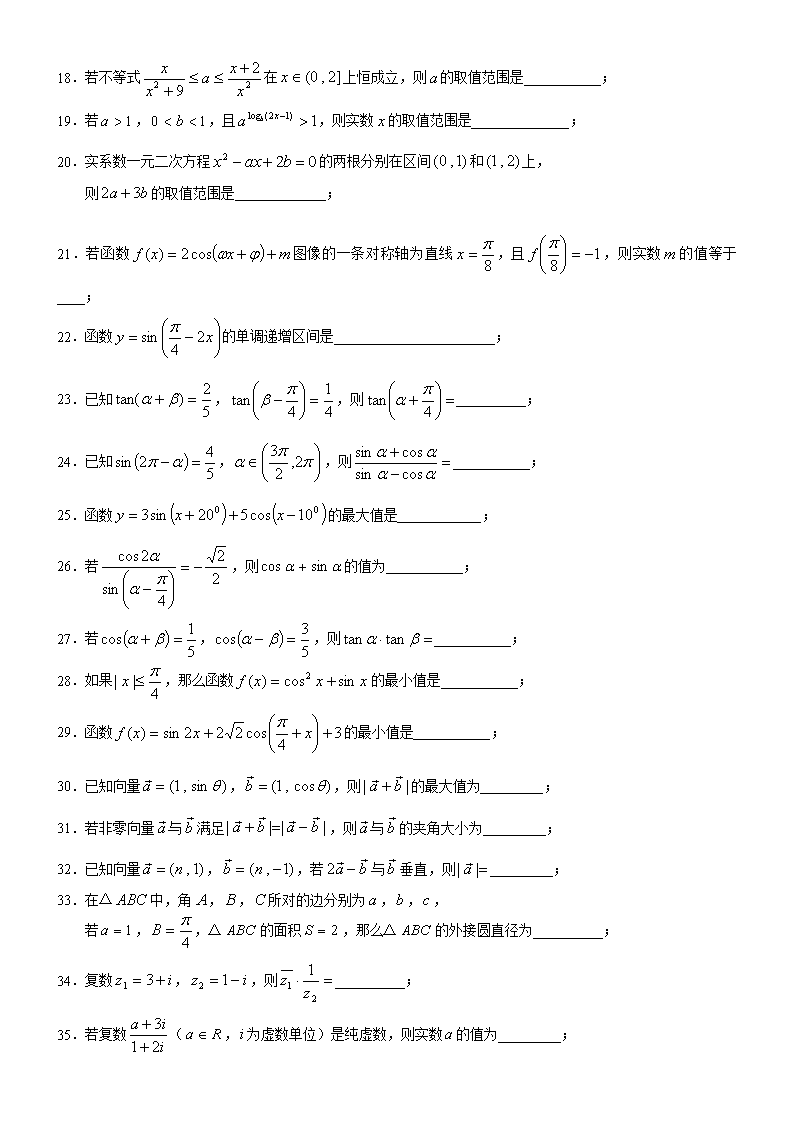

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考数学填空题题
江苏省高考数学填空题训练100题 1.设集合,,则集合且__________; 2.设,若对任意实数,恒成立,则实数的取值范围是________________; 3.已知,且,则实数的值为______________; 4.若,,则____________; 5.已知二次函数(),满足,则________; 6.已知是定义在R上的奇函数,当时,, 则方程的解集是____________________; 7.已知在上是增函数,则的取值范围是________________; 8.已知函数,,如果,则的取值范围是____________; 9.关于的方程有负数解,则实数的取值范围是______________; 10.已知函数满足:对任意实数,,当时,有,且. 写出满足上述条件的一个函数:_____________; 11.定义在区间内的函数满足,则______________; 12.函数()的图像的最低点的坐标是______________; 13.已知正数,满足,则的最小值是___________; 14.设实数,,,满足,,则的取值范围为______________; 15.不等式的解集是_________________; 16.不等式()的解集是___________________; 17.已知 ,则不等式的解集是_________________; 18.若不等式在上恒成立,则的取值范围是___________; 19.若,,且,则实数的取值范围是______________; 20.实系数一元二次方程的两根分别在区间和上, 则的取值范围是_____________; 21.若函数图像的一条对称轴为直线,且,则实数的值等于____; 22.函数的单调递增区间是_______________________; 23.已知,,则__________; 24.已知,,则___________; 25.函数的最大值是____________; 26.若,则的值为___________; 27.若,,则___________; 28.如果,那么函数的最小值是___________; 29.函数的最小值是___________; 30.已知向量,,则的最大值为_________; 31.若非零向量与满足,则与的夹角大小为_________; 32.已知向量,,若与垂直,则_________; 33.在△中,角,,所对的边分别为,,, 若,,△的面积,那么△的外接圆直径为__________; 34.复数,,则__________; 35.若复数(,为虚数单位)是纯虚数,则实数的值为_________; 36.若,且,则的最小值是__________; 37.等差数列的前项之和为,若,则的值为_________; 38.已知数列中,,,那么的值为_________; 39.首项为的等差数列,从第项起为正数,则公差的取值范围是_________; 40.已知一个等差数列的前五项之和是,后五项之和是,又各项之和是,则此数列共有______项; 40.已知数列的通项公式为,从中依次取出第,,,…,,…项, 按原来的顺序排成一个新的数列,则此数列的前项和为______________; 41.在正项等比数列中,,是方程的两个根,则的值为_______; 42.数列中,,,(),则其通项公式为__________; 43.如果直线与直线关于轴对称,那么直线的方程是________________; 44.若平面上两点,,直线与线段恒有公共点,则的取值范围是________; 45.已知△的顶点,若点在轴上,点在直线上,则△的周长的最小值是______; 46.设过点的直线的斜率为,若上恰有三个点到直线的距离等于, 则的值是__________; 47.直线与的两条切线,则该圆的面积等于_________; 48.已知为圆上的动点,则的最大值为______; 49.已知圆和过原点的直线的交点为、,则的值为________; 50.已知、为椭圆的两个焦点,为椭圆上一点, 当时,的取值范围为________________; 51.当满足___________时,曲线与曲线的焦距相等; 52.若椭圆()和双曲线(,)有相同的焦点,, 点是两条曲线的一个交点,则的值为__________; 53.若双曲线经过点,且渐近线方程是,则该双曲线方程是__________________; 54.一个动圆的圆心在抛物线上,且动圆恒与直线相切,则此动圆必经过点__________; 55.过抛物线焦点的直线与抛物线交于、两点,若、在抛物线准线上的射影分别为、, 则___________; 56.长度为的线段的两个端点、都在抛物线(,)上滑动, 则线段的中点到轴的最短距离为___________; 57.已知直线、与平面、,给出下列三个命题: ①若∥,∥,则∥;②若∥,⊥,则⊥;③若⊥,∥,则⊥. 以上命题中正确的是_____________;(写出所有正确命题序号) 58.已知一个平面与正方体的条棱所成的角均为,则_________; 59.已知正四棱锥的体积为,底面对角线的长为,则侧面与底面所成二面角等于__________; 60.正三棱柱的各棱长都为,、分别是、的中点,则的长为________; 61.从,,,,中每次取出不同的三个数字组成三位数,这些三位数的个位数之和为_________; 62.某小组有个男同学和个女同学,从这小组中选取人去完成三项不同的工作,其中女同学至少人, 每项工作至少人,则不同的选派方法的种数为__________; 63.有个球队参加单循环足球比赛,其中个队各比赛了三场就退出了比赛,这两队之间未进行比赛, 这样到比赛结束共赛了场,那么________; 64.一排共个座位,安排甲,乙,丙三人按如下方式就座,每人左、右两边都有空位,且甲必须在乙、丙之间,则不同的坐法共有__________种; 65.现有个参加兴趣小组的名额,分给个班级,每班至少个,则不同的分配方案共___________种; 66.有种不同的树苗需要种植在一条直道的一侧,相邻的两棵树不能是同一种树苗, 若第一棵种下的是甲种树苗,那么第棵树又恰好是甲种树苗的种法共有__________种; 67.从集合中选个不同的数,使这个数成递增的等差数列, D C B A 则这样的数列共有_______组; 68.用种不同的颜色给图中、、、四个区域涂色, 规定每个区域只能涂一种颜色,相邻区域颜色不同, 则有_________种不同的涂色方法; 69.圆周上有个等分圆周的点,以这些点为顶点的钝角三角形或锐角三角形共有________个; 70.某幢楼从二楼到三楼的楼梯共级,上楼可以一步上一级,也可以一步上两级, 若规定从二楼到三楼用步走完,则上楼的方法有___________种; 71.展开式中的系数是____________; 72.若的展开式中各项系数之和为,则展开式的常数项为____________; 73.,则________; 74.若,则__________; 75.盒中有个白球,个红球,从中任取个球,则抽出个白球和个红球的概率是_________; 76.从,,…,这九个数中,随机取个不同的数,则这两个数的和为偶数的概率是________; 77.设集合,,若把满足的集合叫做集合的配集, 则的配集有_______个; 78.设是一个非空集合,是一种运算,如果对于集合中的任意两个元素,,实施运算的结果 仍是集合中的元素,那么说集合对于运算是“封闭”的,已知集合, 若定义运算分别为加法、减法、乘法和除法(除数不为零)四种运算, 则集合对于运算是“封闭”的有_______________________;(写出所有符合条件的运算名称) 79.的定义符号运算 ,则不等式的解集是__________________; 80.我们将一系列值域相同的函数称为“同值函数”,已知,, 试写出的一个“同值函数”___________________;(除一次、二次函数外) 81.有些计算机对表达式的运算处理过程实行“后缀表达式”,运算符号紧跟在运算对象的后面, 按照从左到右的顺序运算,如表达式,其运算为,,,—,*,,, 若计算机进行运算,,,—,*,,那么使此表达式有意义的的范围为____________; 82.设表示不超过的最大整数(例如:,, 则不等式的解集为_______________________; 83.对任意,,记 . 则函数()的最小值是__________; 84.对于数列,定义数列为数列的“差数列”.若,的“差数列”的通项为,则数列的前项和_____________; 85.对于正整数,定义一种满足下列性质的运算“*”:(1);(2), 则用含的代数式表示_____________; 86.若为()的各位数字之和,如,,则. ,,…,,,则__________; 87.如果圆至少覆盖函数的图像的一个最大值与一个最小值, 则的取值范围是________________; 88.设是曲线上的点,,,则最大值是________; 89.已知,,直线,和. 设是()上与,两点距离平方和最小的点, 则△的面积是_________; 90.如右图将网格中的三条线段沿网格线上下或左右平移, 组成一个首尾相连的三角形, 则三条线段一共至少需要移动__________格; 91.已知集合,, 若,则实数的值是_____________; 92.对于任意的函数,在同一坐标系里,与的图像关于__________对称; 93.若不等式对恒成立,则的取值范围是_____________; 94.数列,,,,…,,…的前项和为___________________; 95.在△中,,,,则的值等于_________; 96.设平面向量,,若与的夹角为钝角,则的取值范围是_______________; 97.与圆相切且在坐标轴上截距相等的直线有________条; 98.某企业在今年年初贷款,年利率为,从今年末开始,每年末偿还一定金额,预计年还清, 则每年应偿还的金额为________________; 99.过抛物线(为常数且)的焦点作抛物线的弦,则等于_________; 100.(有关数列极限的题目) (1)计算:__________; (2)计算:___________; (3)计算:___________;(4)若,则常数_________; (5)_________; (6)数列的前项和为,则_________; (7)若常数满足,则___________; (8)设函数,点表示坐标原点,点(为正整数). 若向量,是与的夹角(其中), 设,则_________; 江苏省高考数学填空题训练100题参考答案 1.; 2.; 3.; 4.; 5.; 6.; 7.; 8.; 9.; 10.(不唯一,一般的,均可); 11.; 12.; 13.; 14.; 15.或}; 16.; 17.; 18.; 19.; 20.; 21.或; 22.(); 23.; 24.; 25.; 26.; 27.; 28.; 29.; 30.; 31.90°; 32.; 33.; 34.; 35.; 36.; 37.; 38.; 39.; 40.; 41.; 42.; 43.; 44.; 45.; 46.或; 47.; 48.8; 49.5; 50.; 51.或; 52.; 53.; 54.; 55.90°; 56.; 57.②③; 58.; 59.; 60.; 61.m<5或5查看更多
相关文章
- 当前文档收益归属上传用户