高考数学分类汇编专题十四不等式选讲

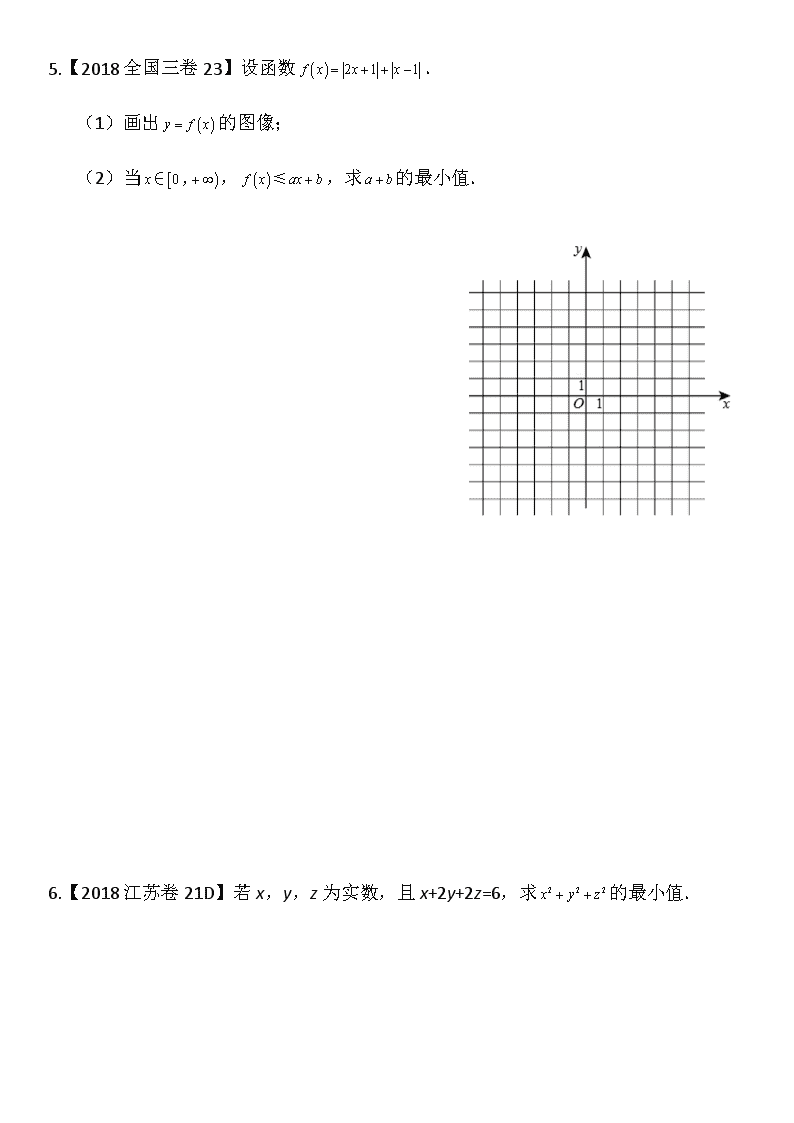
高考数学分类汇编专题十四不等式选讲

不等式选讲 ‎1.(2017·新课标全国卷Ⅰ)已知函数f(x)＝－x2＋ax＋4，g(x)＝|x＋1|＋|x－1|.‎ ‎(1)当a＝1时，求不等式f(x)≥g(x)的解集；‎ ‎(2)若不等式f(x)≥g(x)的解集包含[－1,1]，求a的取值范围．‎ ‎2．(2016·新课标全国卷Ⅲ，24)已知函数f(x)＝|2x－a|＋a.‎ ‎(1)当a＝2时，求不等式f(x)≤6的解集；‎ ‎(2)设函数g(x)＝|2x－1|.当x∈R时，f(x)＋g(x)≥3，求a的取值范围．‎ ‎]‎ ‎3.【2018全国一卷23】已知.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若时不等式成立，求的取值范围.‎ ‎4.【2018全国二卷23】设函数．‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若，求的取值范围．‎ ‎5.【2018全国三卷23】设函数．‎ ‎（1）画出的图像；‎ ‎（2）当，，求的最小值．‎ ‎6.【2018江苏卷21D】若x，y，z为实数，且x+2y+2z=6，求的最小值．‎ 参考答案 解析：(1)当a＝1时，不等式f(x)≥g(x)等价于 x2－x＋|x＋1|＋|x－1|－4≤0.①‎ 当x＜－1时，①式化为x2－3x－4≤0，无解；‎ 当－1≤x≤1时，①式化为x2－x－2≤0，从而－1≤x≤1；‎ 当x＞1时，①式化为x2＋x－4≤0，‎ 从而1＜x≤.‎ 所以f(x)≥g(x)的解集为x－1≤x≤.‎ ‎(2)当x∈[－1,1]时，g(x)＝2，‎ 所以f(x)≥g(x)的解集包含[－1,1]，等价于当x∈[－1,1]时f(x)≥2.‎ 又f(x)在[－1,1]的最小值必为f(－1)与f(1)之一，所以f(－1)≥2且f(1)≥2，得－1≤a≤1.‎ 所以a的取值范围为[－1,1].‎ 解析：(1)当a＝2时，f(x)＝|2x－2|＋2.‎ 解不等式|2x－2|＋2≤6得－1≤x≤3.‎ 因此f(x)≤6的解集为{x|－1≤x≤3}．‎ ‎(2)当x∈R时，f(x)＋g(x)＝|2x－a|＋a＋|1－2x|≥|2x－a＋1－2x|＋a＝|1－a|＋a，‎ 所以当x∈R时，f(x)＋g(x)≥3等价于|1－a|＋a≥3.①‎ 当a≤1时，①等价于1－a＋a≥3，无解．‎ 当a＞1时，①等价于a－1＋a≥3，解得a≥2.‎ 所以a的取值范围是[2，＋∞)．‎ ‎1.解： （1）当时，，即 故不等式的解集为．‎ ‎（2）当时成立等价于当时成立．‎ 若，则当时；‎ 若，的解集为，所以，故．‎ 综上，的取值范围为．‎ ‎2.解：（1）当时，‎ 可得的解集为．‎ ‎（2）等价于．‎ 而，且当时等号成立．故等价于．‎ 由可得或，所以的取值范围是．‎ ‎3.解：（1）的图像如图所示．‎ ‎（2）由（1）知，的图像与轴交点的纵坐标为，且各部分所在直线斜率的最大值为，故当且仅当且时，在成立，因此的最小值为．‎ ‎4.证明：由柯西不等式，得．‎ 因为，所以，‎ 当且仅当时，不等式取等号，此时，‎ 所以的最小值为4．‎