高考大题题型总结

高考大题题型总结

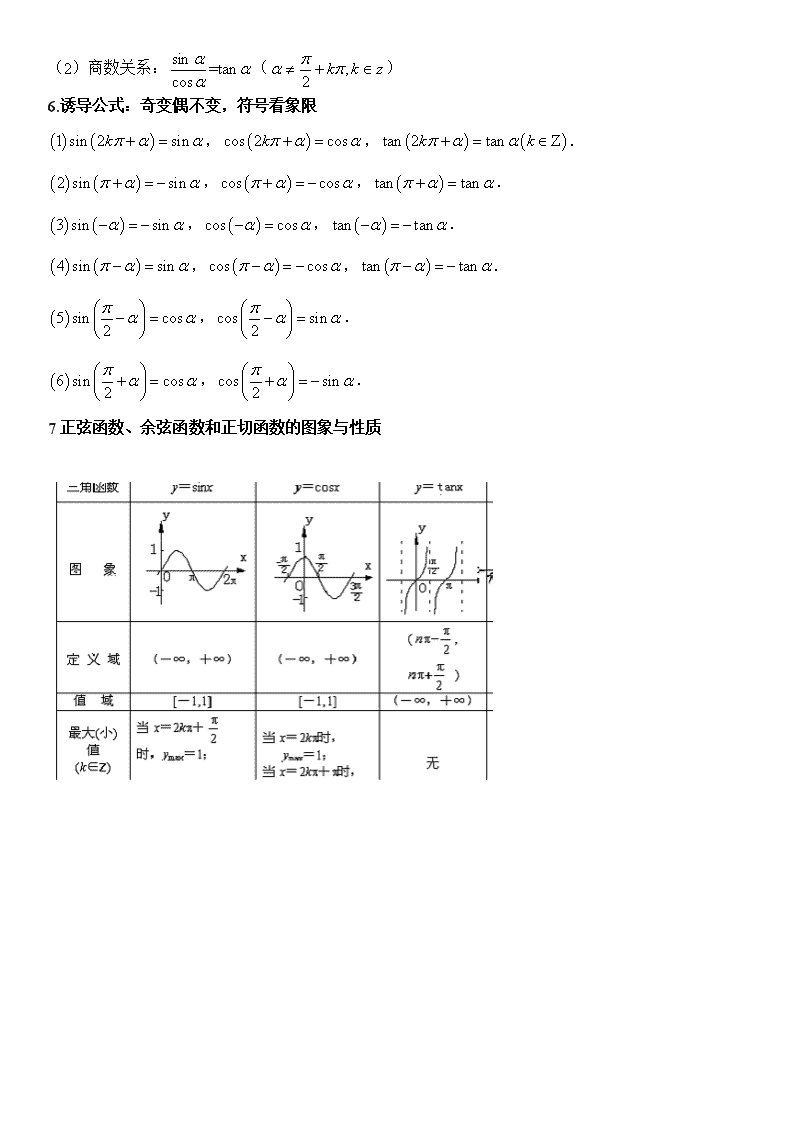
‎ 三角函数 ‎ 一 知识点总结 ‎ 1．角度制与弧度制的互化： ‎ ‎1rad＝°≈57.30°=57°18ˊ． 1°＝≈0.01745（rad）‎ ‎2.弧长及扇形面积公式 ‎ 弧长公式： 扇形面积公式:S=‎ ‎----是圆心角且为弧度制。 r-----是扇形半径 ‎3.任意角的三角函数 ‎ 设是一个任意角，它的终边上一点p（x,y）, r=‎ ‎(1)正弦sin= 余弦cos= 正切tan=‎ ‎(2)各象限的符号：‎ ‎— +‎ ‎+ —‎ ‎-‎ x y ‎++‎ O ‎— —‎ ‎+‎ x y O ‎— +‎ ‎ ‎ ‎— +‎ y O sin cos tan ‎4、三角函数线 ‎ 正弦线：MP; 余弦线：OM; 正切线： AT.‎ ‎5.同角三角函数的基本关系：‎ ‎（1）平方关系：sin2+ cos2=1。‎ ‎（2）商数关系：=tan（）‎ ‎6.诱导公式：奇变偶不变，符号看象限 ‎，，．‎ ‎，，．‎ ‎，，．‎ ‎，，．‎ ‎，．‎ ‎，．‎ ‎7正弦函数、余弦函数和正切函数的图象与性质 8. 三角函数的伸缩变化 两角和与差的三角函数关系 sin()=sin·coscos·sin cos()=cos·cossin·sin 9. 三角函数公式：‎ 倍角公式 sin2=2sin·cos cos2=cos2-sin2‎ ‎=2cos2-1‎ ‎=1-2sin2‎ ‎10．正弦定理 ： ‎ ‎.‎ ‎11.余弦定理：‎ ‎;‎ ‎;‎ ‎.‎ 三角形面积定理..‎ 二 、三角函数常考题型 三角函数题是高考数学试卷的第一道解答题，试题难度一般不大，但其战略意义重大，所以稳拿该题12分对文理科学生都至关重要。分析近年高考试卷，可以发现，三角解答题多数喜欢和平面向量综合在一起，且向量为辅，三角为主，主要有以下三类：‎ 一、运用同角三角函数关系、诱导公式、和、差、倍、半等公式进行化简求值类。‎ 例1 已知向量。‎ ‎（1）若，求的取值范围；‎ ‎（2）函数，若对任意，恒有,求的取值范围。‎ 解：（1），‎ 即。‎ ‎（2）。‎ ‎，又 二、运用三角函数性质解题，通常考查正弦、余弦函数的单调性、周期性、最值、对称轴及对称中心。‎ 例3 已知向量, ，, ，，‎ ‎ （1）求的值；‎ ‎ （2）设函数，求x为何值时，取得最大值，最大 值是多少，并求的单调增区间。‎ 解：（1），,∴,‎ ‎，∴,∴，.‎ ‎（2）‎ ‎,∵，‎ ‎∴,∴当时，,要使单调递增，‎ ‎∴,,又，∴的单调增区间为.‎ 三、解三角形问题，判断三角形形状，正余弦定理的应用。‎ 例6 在△中,角A,B ,的对边分别为a,,c．已知向量,,且．‎ ‎（1）求角的大小； （2）若,求角A的值。‎ 解: （1）由得；　整理得．‎ 即，又．又因为,所以． ‎ ‎（2）因为，所以, 故． ‎ 由．即,‎ 所以．即．因为，所以,‎ 故或,∴或． ‎ 三角函数的小题涉及三角函数的所有知识点，因此，熟练掌握公式和性质是解好小题的必要条件，在日常训练中一定要改掉边做题边看公式的坏习惯。再者，填空题答案书写的规范也需反复强调。‎ 数列 一、 知识点 ‎1、数列的通项公式与前n项的和的关系 ‎( 数列的前n项的和为).‎ ‎2、等差数列的通项公式 ‎；‎ ‎3、等差数列其前n项和公式为 ‎.‎ ‎4、等比数列的通项公式 ‎；‎ ‎5、等比数列前n项的和公式为 ‎ 或 .‎ 二、 高考常见题型 题型一：数列的通项公式的求法 A、定义法：①等差数列通项公式；②等比数列通项公式。‎ B、公式法：已知（即）求，用作差法：。‎ ‎ 例．已知数列的前项和满足．求数列的通项公式。‎ 解：由 ‎ 当时，有 ‎……，‎ 经验证也满足上式，所以 C、累加法：‎ 若求：。‎ D、累乘法：已知求，用累乘法：。‎ E、已知递推关系求，用构造法（构造等差、等比数列）。‎ ‎ ①为常数，即递推公式为（其中p，q均为常数，）。‎ 解法：转化为：，其中，再利用换元法转化为等比数列求解。‎ 例. 已知数列中，，，求.‎ 解：设递推公式可以转化为即.故递推公式为,令，则,且.所以是以为首项，2为公比的等比数列，则, 所以.‎ 二.数列的前n项求和的求法 ‎1.公式法：①等差数列求和公式；②等比数列求和公式，‎ 特别声明：运用等比数列求和公式，务必检查其公比与1的关系，必要时需分类讨论.‎ 常用公式：，，‎ ‎2.分组求和法：在直接运用公式法求和有困难时，常将“和式”中“同类项”先合并在一起，再运用公式法求和. ‎ ‎3.倒序相加法：若和式中到首尾距离相等的两项和有其共性或数列的通项与组合数相关联，则常可考虑选用倒序相加法，发挥其共性的作用求和（这也是等差数列前和公式的推导方法）.‎ 例3、求的值 解：设…………. ①‎ 将①式右边反序得 ‎…………..② （反序） ‎ 又因为 ‎ ‎①+②得 （反序相加）‎ ‎＝89 ‎ ‎∴ S＝44.5‎ ‎4.错位相减法：如果数列的通项是由一个等差数列的通项与一个等比数列的通项相乘构成，那么常选用错位相减法（这也是等比数列前和公式的推导方法）.‎ 例4、 求和：………………………①‎ 解：由题可知，{}的通项是等差数列{2n－1}的通项与等比数列{}的通项之积 设………………………. ② （设制错位）‎ ‎①－②得 （错位相减）‎ 再利用等比数列的求和公式得：‎ ‎ ∴ ‎ 5. 裂项相消法：如果数列的通项可“分裂成两项差”的形式，且相邻项分裂后相关联，那么常选用裂项相消法求和 ‎ 常用裂项形式有：‎ ‎①；②；‎ ‎③，；‎ ‎④ ；⑤；‎ ‎ ‎ ‎6.通项转换法：先对通项进行变形，发现其内在特征，再运用分组求和法求和。‎ 例8 、求之和.‎ 解：由于 （找通项及特征）‎ ‎∴ ‎ ‎＝ （分组求和）‎ ‎＝‎ ‎＝‎ ‎＝‎ ‎ 导数 一、知识点总结 ‎1、导数的几何意义：‎ ‎ 函数在点处的导数的几何意义就是曲线在点处的切线的斜率，也就是说，曲线在点P处的切线的斜率是，切线方程为 ‎ 2.、几种常见函数的导数：‎ ‎①；②； ③；④；‎ ‎⑤；⑥； ⑦；⑧‎ ‎ 3、导数的运算法则 （1） ‎. （2）. （3）‎ ‎4、复合函数的求导法则 ‎ 设函数在点处有导数，函数在点处的对应点U处有导数，则复合函数在点处有导数，且，或写作.‎ ‎5、极值的判别方法：（极值是在附近所有的点，都有＜，则是函数的极大值，极小值同理）‎ 当函数在点处连续时，‎ ‎①如果在附近的左侧＞0，右侧＜0，那么是极大值；‎ ‎②如果在附近的左侧＜0，右侧＞0，那么是极小值 极值与最值区别：极值是在局部对函数值进行比较，最值是在整体区间上对函数值进行比较.‎ 二、常考题型总结 题型一：利用导数研究函数的极值、最值。‎ ‎1． 在区间上的最大值是？ ‎ ‎2．已知函数处有极大值，则常数C？‎ ‎3．函数有极小值 ？,极大值？ ‎ ‎ ‎ 题型二：利用导数几何意义求切线方程 ‎1．曲线在点处的切线方程是 ‎ ‎2．若曲线在P点处的切线平行于直线，则P点的坐标为 （1，0） ‎ ‎4．求下列直线的方程：‎ ‎ （1）曲线在P(-1,1)处的切线； （2）曲线过点P(3,5)的切线；‎ 解：（1）‎ ‎ 所以切线方程为 ‎ （2）显然点P（3，5）不在曲线上，所以可设切点为，则①又函数的导数为，‎ 所以过点的切线的斜率为，又切线过、P(3,5)点，所以有②，由①②联立方程组得，，即切点为（1，1）时，切线斜率为；当切点为（5，25）时，切线斜率为；所以所求的切线有两条，方程分别为 题型三：利用导数研究函数的单调性，极值、最值 ‎ 1．已知函数的切线方程为y=3x+1 ‎ ‎ （Ⅰ）若函数处有极值，求的表达式；‎ ‎ （Ⅱ）在（Ⅰ）的条件下，求函数在[－3，1]上的最大值；‎ ‎ （Ⅲ）若函数在区间[－2，1]上单调递增，求实数b的取值范围 ‎ 解：（1）由 过的切线方程为：‎ ‎ ‎ ‎①‎ ‎②‎ 而过 故 ‎ ‎∵ ③ ‎ 由①②③得 a=2，b=－4，c=5 ∴ ‎ ‎（2）‎ 当 ‎ 又在[－3，1]上最大值是13。 ‎ ‎（3）y=f(x)在[－2，1]上单调递增，又由①知2a+b=0。 ‎ 依题意在[－2，1]上恒有≥0，即 ‎ ‎①当；‎ ‎②当；‎ ‎③当 ‎ 综上所述，参数b的取值范围是 题型四：利用导数研究函数的图象 ‎1．如右图：是f（x）的导函数， 的图象如右图所示，则f（x）的图象只可能是（ D ）‎ ‎（A） （B） （C） （D）‎ ‎2．函数( A )‎ x y o ‎4‎ ‎-4‎ ‎2‎ ‎4‎ ‎-4‎ ‎2‎ ‎-2‎ ‎-2‎ x y o ‎4‎ ‎-4‎ ‎2‎ ‎4‎ ‎-4‎ ‎2‎ ‎-2‎ ‎-2‎ x y y ‎4‎ o ‎-4‎ ‎2‎ ‎4‎ ‎-4‎ ‎2‎ ‎-2‎ ‎-2‎ ‎6‎ ‎6‎ ‎6‎ ‎6‎ y x ‎-4‎ ‎-2‎ o ‎4‎ ‎2‎ ‎2‎ ‎4‎ ‎3．方程 ( B )‎ ‎ A、0 B、1 C、2 D、3‎ 题型五：求参数取值范围、恒成立及存在性问题 ‎ A、分离常数法 ‎ 例1、已知函数.（Ⅰ）求的最小值；（Ⅱ）若对所有都有，求实数的取值范围.学科网 解：(Ⅰ).‎ ‎ 又易知 ‎ ‎ ‎ 所以 ‎（Ⅱ）依题意，得在上恒成立，即不等式对于恒成立 （分离常数）. ‎ ‎ 令， 则. 当时，因为， ‎ 故是上的增函数， 所以 的最小值是，所以的取值范围是. ‎ B、与二次函数的性质、单调性、不等式等相联系 求解策略：‎ 1、 利用“要使成立，只需使函数的最小值恒成立即可；要使成立，只需使函数的最大值恒成立即可 ‎2、已知函数的单调性及单调区间，则转化为关于导数大于或者小于0在给定区间上恒成立的问题 ‎3、利用子空间的思想，即首先求出函数的单调增或减区间，然后让题所给的区间是所求区间的子集 类型1．参数放在函数表达式上 例１． 设函数．‎ ‎（１）由 ‎（２）方法１：‎ ‎ 方法２：‎ 方法３．‎ 解题方法总结：求后，若能因式分解则先因式分解，讨论=0两根的大小判断函数的单调性，若不能因式分解可利用函数单调性的充要条件转化为恒成立问题.‎ 类型2．参数放在区间边界上 例２．已知函数过原点和点ｐ(-1,2),若曲线在点P处的切线与直线且切线的倾斜角为钝角.‎ (1) 求的表达式 (2) 若在区间[2m-1,m+1]上递增,求m的取值范围.‎ 略解 (1)‎ 总结:先判断函数的单调性,再保证问题中的区间是函数单调递增(递减)区间的一个子区间即可.‎ C、已知不等式在某区间上恒成立，求参数的取值范围 类型１．参数放在不等式上 例3.已知 (1) 求ａ、ｂ的值及函数的单调区间．‎ (2) 若对恒成立，求ｃ的取值范围．‎ 略解：(1)‎ ‎ ‎ 总结:区间给定情况下,转化为求函数在给定区间上的最值.‎ 类型2．参数放在区间上 例４．已知三次函数图象上点(1,8)处的切线经过点(3,0),并且在x=3处有极值.‎ （１） 求的解析式.‎ （２） 当时, >0恒成立,求实数m的取值范围.‎ 分析:(1)‎ D、知函数图象的交点情况，求参数的取值范围．‎ 解题思路：1 画出两个图像，即穿线图和趋势图（先增后减再增或者先减后增再减）‎ ‎ 2 由趋势图结合根的个数写不等式（主要看极值与0的关系）‎ ‎ 3 解不等式 例5.已知函数处取得极值 (1) 求函数的解析式.‎ (2) 若过点可作曲线y=的三条切线,求实数m的取值范围.‎ 略解(1)求得 ‎ (2)设切点为 总结:从函数的极值符号及单调性来保证函数图象与x轴交点个数.‎ ‎ 在文科数学中,涉及到高次函数问题一般可用导数知识解决,只要把导数的几何意义,用导数求函数的极值及最值,用导数求函数单调性等这些基础知识搞清弄懂,那么,利用导数求参数的取值范围这个问题即可迎刃而解.‎ ‎ ‎ 圆锥曲线 一、 知识点总结 ‎（一）圆 ‎1、定义：点集｛M｜｜OM｜=r｝，其中定点O为圆心，定长r为半径.‎ ‎2、方程：(1)标准方程：圆心在c(a,b)，半径为r的圆方程是(x-a)2+(y-b)2=r2‎ ‎ 圆心在坐标原点，半径为r的圆方程是x2+y2=r2‎ ‎(2)一般方程：①当D2+E2-4F＞0时，一元二次方程x2+y2+Dx+Ey+F=0叫做圆的一般方程，圆心为半径是。配方，将方程x2+y2+Dx+Ey+F=0化为(x+)2+(y+)2=‎ ‎②当D2+E2-4F=0时，方程表示一个点(-,-);‎ ‎③当D2+E2-4F＜0时，方程不表示任何图形.‎ 点与圆的位置关系 已知圆心C(a,b),半径为r,点M的坐标为(x0,y0)，则｜MC｜＜r点M在圆C内，｜MC｜=r点M在圆C上，｜MC｜＞r 点M在圆C内，其中｜MC｜=。‎ 直线和圆的位置关系：①直线和圆有相交、相切、相离三种位置关系：直线与圆相交有两个公共点；直线与圆相切有一个公共点；直线与圆相离没有公共点。‎ ‎②直线和圆的位置关系的判定：(i)判别式法；(ii)利用圆心C(a,b)到直线Ax+By+C=0的距离与半径r的大小关系来判定。‎ ‎(二）椭圆、双曲线、抛物线：‎ 椭圆、双曲线、抛物线性质对比 椭圆 双曲线 抛物线 定义 ‎1．到两定点F1,F2的距离之和为定值2a(2a>|F1F2|)的点的轨迹 ‎2．与定点和直线的距离之比为定值e的点的轨迹.（01）‎ 与定点和直线的距离相等的点的轨迹.‎ 轨迹条件 点集：({M｜｜MF1+｜MF2｜=2a,｜F 1F2｜＜2a}‎ 点集：{M｜｜MF1｜-｜MF2｜.‎ ‎=±2a,｜F2F2｜＞2a}.‎ 点集{M｜ ｜MF｜=点M到直线l的距离}.‎ 图形 方 程 标准方程 ‎(>0)‎ ‎(a>0,b>0)‎ 参数方程 ‎(t为参数)‎ 范围 ‎─a£x£a，─b£y£b ‎|x| ³ a，yÎR x³0‎ 中心 原点O（0，0）‎ 原点O（0，0）‎ 顶点 ‎(a,0), (─a,0), (0,b) , (0,─b)‎ ‎(a,0), (─a,0)‎ ‎(0,0)‎ 对称轴 x轴，y轴；‎ 长轴长2a,短轴长2b x轴，y轴;‎ 实轴长2a, 虚轴长2b.‎ x轴 焦点 F1(c,0), F2(─c,0)‎ F1(c,0), F2(─c,0)‎ 准 线 x=±‎ 准线垂直于长轴，且在椭圆外.‎ x=±‎ 准线垂直于实轴，且在两顶点的内侧.‎ x=-‎ 准线与焦点位于顶点两侧，且到顶点的距离相等.‎ 焦距 ‎2c （c=）‎ ‎2c （c=）‎ 离心率 e=1‎ ‎【备注1】双曲线：‎ ‎⑶等轴双曲线：双曲线称为等轴双曲线，其渐近线方程为，离心率.‎ ‎⑷共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲线.与互为共轭双曲线，它们具有共同的渐近线：.‎ ‎⑸共渐近线的双曲线系方程：的渐近线方程为如果双曲线的渐近线为时，它的双曲线方程可设为.‎ ‎【备注2】抛物线：‎ ‎（1）抛物线=2px(p>0)的焦点坐标是(,0)，准线方程x=- ，开口向右；抛物线=-2px(p>0)的焦点坐标是(-,0)，准线方程x=，开口向左；抛物线=2py(p>0)的焦点坐标是(0,)，准线方程y=-　，开口向上；‎ 抛物线=-2py（p>0）的焦点坐标是（0,-），准线方程y=，开口向下.‎ ‎（2）抛物线=2px(p>0)上的点M(x0,y0)与焦点F的距离；抛物线=-2px(p>0)上的点M(x0,y0)与焦点F的距离 ‎（3）设抛物线的标准方程为=2px(p>0)，则抛物线的焦点到其顶点的距离为，顶点到准线的距离，焦点到准线的距离为p.‎ ‎（4）已知过抛物线=2px(p>0)焦点的直线交抛物线于A、B两点，则线段AB称为焦点弦，设A(x1,y1),B(x2,y2)，则弦长=+p或(α为直线AB的倾斜角)，，(叫做焦半径).‎ 二、常考题型 ‎ 常用知识点总结 ‎1、中点坐标公式：，其中是点的中点坐标。‎ ‎2、弦长公式：若点在直线上，‎ 则，这是同点纵横坐标变换，是两大坐标变换技巧之一，‎ 或者 ‎。‎ ‎3、两条直线垂直：则 两条直线垂直，则直线所在的向量 4、 韦达定理：若一元二次方程有两个不同的根，则。‎ ‎ 题型一、数形结合确定直线和圆锥曲线的位置关系 解题思路：①联立方程组→→②求出式★→→③利用韦达定理、判别式 ‎ →→④寻求“目标”的实现 ‎ （1）相交：直线与圆锥曲线相交； ‎ ‎ （2）相切：直线与圆锥曲线相切；‎ ‎ （3）相离：直线与圆锥曲线相离；‎ 例题1、已知直线与椭圆始终有交点，求的取值范围 解：根据直线的方程可知，直线恒过定点（0，1），椭圆过动点，如果直线和椭圆始终有交点，则，即。‎ 规律提示：通过直线的代数形式，可以看出直线的特点：‎ 题型二、焦点三角形，焦半径，焦点弦问题 ‎（1）焦点三角形 ‎ 定义：椭圆（双曲线）上一点和两焦点组成的三角形叫焦点三角形；有一个角为直角的焦 点三角形叫焦点直角三角形。‎ ‎1：该三角形一边长为焦距，另两边的和（差）为定值。‎ ‎2：椭圆焦点三角形中，顶点在椭圆上的点到另两点的张角中，以短轴端点到这两点的张角最大。‎ ‎（此处具体知识点省略，看笔记）‎ （2） 焦半径，焦点弦 若抛物线的方程为y2＝2px（p＞0），过抛物线的焦点F（，0）的直线交抛物线与 A（x1，y1）、B（x2，y2）两点，则 ‎(1) y1y2＝－p2；x1x2＝；‎ ‎(2)| AB|＝x1＋x2＋p；通径=2P ‎(3)；‎ ‎(4) 过A、B两点作准线的垂线，垂足分别为A/、B/，F抛物线的焦点，则∠A/FB/＝900；‎ ‎(5) 以弦AB为直径的圆与准线相切。‎ ‎(6) 设A， B是抛物线y2＝2px上的两点，O为原点， 则OA⊥OB的充要条件是直线AB恒过定点(2p，0)‎ 例题（1）短轴长为，离心率的椭圆的两焦点为、，过作直线交椭圆于A、B两点，则的周长为________‎ ‎（2）设P是等轴双曲线右支上一点，F1、F2是左右焦点，若，|PF1|=6，则该双曲线的方程为 ‎ ‎（3）双曲线的虚轴长为4，离心率e＝，F1、F2是它的左右焦点，若过F1的直线与双曲线的左支交于A、B两点，且是与等差中项，则＝_______‎ ‎（4）已知双曲线的离心率为2，F1、F2是左右焦点，P为双曲线上一点，且，．求该双曲线的标准方程。‎ 题型三、动点轨迹方程问题 ‎1、直接法w.w.w.k.s.5.u.c.o.m 当所求动点的要满足的条件简单明确时，直接按“建系设点、列出条件、代入坐标、整理化简、限制说明”五个基本步骤求轨迹方程, 称之直接法.‎ 例1．点与定点的距离和它到定直线的距离的比是，求点的轨迹方程式，并说明轨迹是什么图形．‎ 变式：已知动点P到定点F(1,0)和直线的距离之和等于4，求P的轨迹方程．‎ ‎2、待定系数法：‎ 已知轨迹是什么图形，先设出其标准方程，再求出参数。‎ 例2、    已知椭圆的焦点坐标为和，且经过点，求椭圆的标准方程。‎ 变式：抛物线的顶点在原点，以轴为对称轴，经过焦点且倾斜角为的直线，被抛物线截得的弦长为8，试求抛物线的方程。‎ ‎3、定义法：定义法是指先分析、说明动点的轨迹满足某种特殊曲线（如圆、椭圆、双曲线、抛物线等）的定义或特征，再求出该曲线的相关参量，从而得到轨迹方程.‎ 例3、求与圆及都外切的动圆圆心的轨迹方程 解：设动圆的半径为r，则由动圆与定圆都外切得 ‎，‎ 又因为，‎ 由双曲线的定义可知，点M的轨迹是双曲线的一支 所求动圆圆心的轨迹是双曲线的一支，其方程为：‎ 变式：（1）、一动圆与圆外切，同时与圆内切，求动圆圆心的轨迹方程式，并说明它是什么曲线．‎ ‎（2 、 已知的底边BC长为12，且底边固定，顶点A是动点，使，求点A的轨迹 分析：首先建立坐标系，由于点A的运动规律不易用坐标表示，注意条件的运用，可利用正弦定理将其化为边的关系，注意有关限制条件 解：以底边BC 为轴，底边BC的中点为原点建立坐标系，这时 ‎，由得 ‎,即 所以，点A的轨迹是以为焦点，2=6的双曲线的左支 其方程为：‎ ‎4、代入法 当题目中有多个动点时，将其他动点的坐标用所求动点的坐标来表示，再代入到其他动点要满足的条件或轨迹方程中，整理即得到动点的轨迹方程，称之代入法，也称相关点法、转移法.‎ 例4：点A位于双曲线上，是它的两个焦点，求的重心G的轨迹方程 ‎ 分析：要求重心的轨迹方程，必须知道三角形的三个顶点的坐标，利用相关点法进行求解 注意限制条件 ‎ 解：设的重心G的坐标为，则点A的坐标为 因为点A位于双曲线上，从而有 ‎，即 所以，的重心G的轨迹方程为 ‎ y Q O x N P 变式：如图，从双曲线上一点引直线 的垂线，垂足为，求线段的中点的轨迹方程.‎ 解：设，则.在直线上，‎ ‎① 又得即.②‎ 联解①②得.又点在双曲线上，，化简整理得：，此即动点的轨迹方程.‎ ‎5、参数法 ‎ 参数法是指先引入一个中间变量（参数），使所求动点的横、纵坐标间建立起联系，然后再从所求式子中消去参数，得到间的直接关系式，即得到所求轨迹方程.‎ 例5 过抛物线（）的顶点作两条互相垂直的弦、，求弦的中点的轨迹方程.‎ 解：设，直线的斜率为，则直线的斜率为.直线OA的方程为，由解得，即，同理可得.‎ 由中点坐标公式，得，消去，得，此即点的轨迹方程.‎ ‎ 6、交轨法 求两曲线的交点轨迹时，可由方程直接消去参数，或者先引入参数来建立这些动曲线的联系，然后消去参数来得到轨迹方程，称之交轨法.‎ x A1‎ A2‎ O y N M P 例6 如右图，垂直于轴的直线交双曲线于 ‎、两点，为双曲线的左、右顶点，求直线与 的交点的轨迹方程，并指出轨迹的形状.‎ 解：设及，又，可得 直线的方程为①；直线的方程为②.‎ ‎①×②得③. 又，代入③得，化简得，此即点的轨迹方程. 当时，点的轨迹是以原点为圆心、为半径的圆；当时，点的轨迹是椭圆.‎ 题型四、共线问题 解题思路：‎ ‎ 1、取两点确立一条直线，计算解析式，然后带入第三点验证 ‎ 2、向量法证明 ‎ 3、利用点差法求出AB、AC直线的斜率，相等即共线 例题5、设过点D(0,3)的直线交曲线M：于P、Q两点，且,求实数的取值范围。‎ 解：设P(x1,y1),Q(x2,y2),(x1,y1-3)=(x2,y2-3)即 判别式法、韦达定理法、配凑法 设直线PQ的方程为：，由消y整理后，得 P、Q是曲线M上的两点 ＝ 即 ① 由韦达定理得： 即 ② 由①得，代入②，整理得 ， 解之得 当直线PQ的斜率不存在，即时，易知或。 总之实数的取值范围是 题型五、定点问题 ‎（1）A、B是抛物线y2＝2px（p＞0）上的两点，且OA⊥OB（O为坐标原点）‎ 求证：直线AB经过一个定点；‎ ‎（2）抛物线y2＝2px（p＞0）上有两个动点A、B及一定点M（p，p），F为焦点；若|AF|、|MF|、|BF|成等差数列，求证：线段AB的垂直平分线过定点。‎ 例3图 x y B O A M F 题型六、存在性问题：（存在点，存在直线y=kx+m，存在实数，存在图形：三角形（等比、等腰、直角），四边形（矩形、菱形、正方形），圆）‎ 设椭圆E: （a,b>0）过M（2，） ，N(,1)两点，O为坐标原点，‎ ‎（I）求椭圆E的方程；‎ ‎（II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。‎ 解:（1）因为椭圆E: （a,b>0）过M（2，） ，N(,1)两点,‎ 所以解得所以椭圆E的方程为 ‎（2）假设存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且,设该圆的切线方程为解方程组得,即, ‎ 则△=,即 ‎,要使,需使,即,所以,所以又,所以,所以,即或,因为直线 为圆心在原点的圆的一条切线,所以圆的半径为,,,所求的圆为,此时圆的切线都满足或,而当切线的斜率不存在时切线为与椭圆的两个交点为或满足,综上, 存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且.‎ 因为,‎ 所以,‎ ‎, ‎ ‎①当时 因为所以,所以,‎ 所以当且仅当时取”=”. ‎ ② 当时,.‎ ③ 当AB的斜率不存在时, 两个交点为或,所以此时,‎ 综上, |AB |的取值范围为即: ‎ 例8图 x y P F O L A N P N 题型七、最值问题 ‎ （1）如图所示，若A（3，2），F为抛物线y2＝2x的焦点，求|PF|＋|PA|的最小值，以及取得最小值时点P的坐标。‎ 变式：若A（3，5）呢？‎ ‎（2）.定长为3的线段AB的端点A、B在抛物线上移动，求AB中点到轴距离的最小值，并求此时AB中点M的坐标。‎ ‎（3）若，且，则的最大值是___，的最小值是 ‎ ‎（4）以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时，则椭圆长轴的最小值为__‎ ‎！注意圆锥曲线与向量的联系 ‎ （1）给出与相交,等于已知过的中点;‎ ‎（2）给出,等于已知是的中点;‎ ‎（3）给出,等于已知与的中点三点共线;‎ ‎（4） 给出以下情形之一：①；②存在实数；③若存在实数,等于已知三点共线.‎ ‎（5） 给出,等于已知,即是直角,给出,等于已知是钝角, 给出,等于已知是锐角,‎ ‎（6）在平行四边形中，给出，等于已知是菱形;‎ ‎（7） 在平行四边形中，给出，等于已知是矩形;‎ ‎（8）在中，给出，等于已知是的外心（三角形外接圆的圆心，三角形的外心是三角形三边垂直平分线的交点）；‎ ‎（9） 在中，给出，等于已知是的重心（三角形的重心是三角形三条中线的交点）；‎ ‎（10）在中，给出，等于已知是的垂心（三角形的垂心是三角形三条高的交点）；‎ ‎（11）在中，给出等于已知通过的内心；‎ ‎（12）在中，给出等于已知是的内心（‎ 三角形内切圆的圆心，三角形的内心是三角形三条角平分线的交点）；‎ ‎（13） 在中，给出,等于已知是中边的中线;‎