新课标高考物理可能考的第一道大题汇总

新课标高考物理可能考的第一道大题汇总

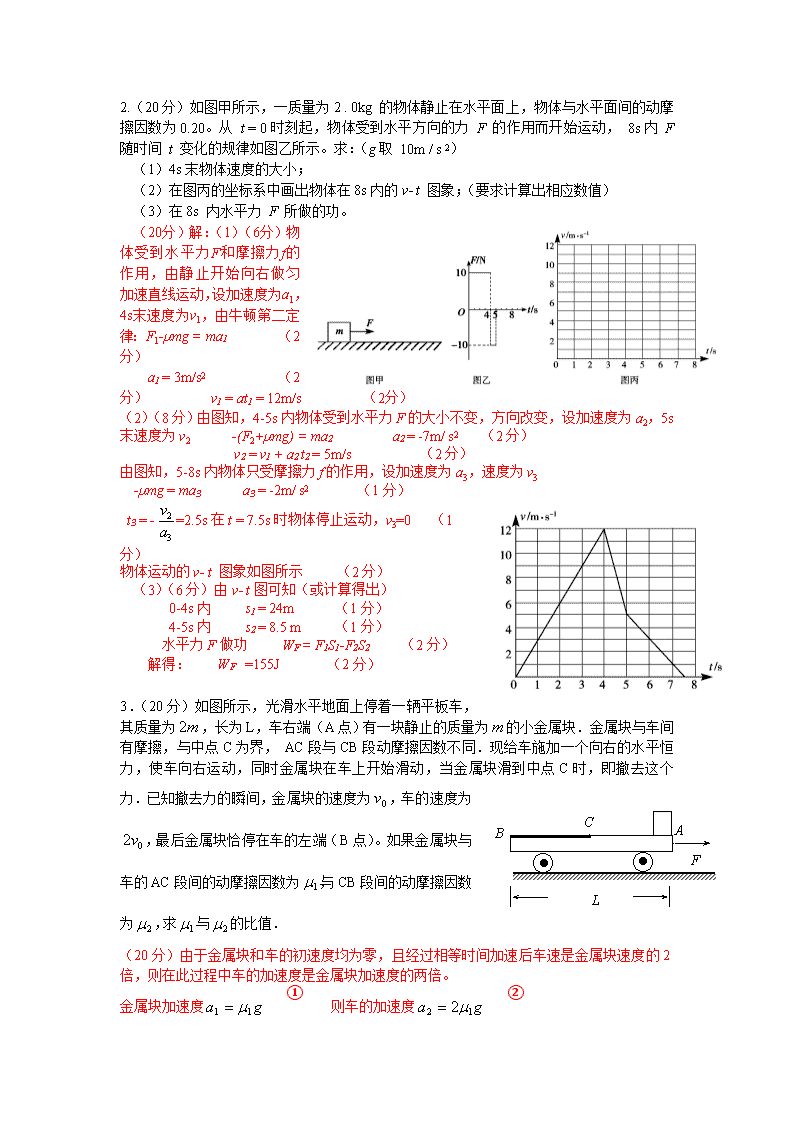
‎2.（20分）如图甲所示，一质量为2 . 0kg 的物体静止在水平面上，物体与水平面间的动摩擦因数为0.20。从 t = 0时刻起，物体受到水平方向的力 F 的作用而开始运动， 8s内 F 随时间 t 变化的规律如图乙所示。求：（g取 10m / s 2）‎ ‎（1）4s末物体速度的大小；‎ ‎（2）在图丙的坐标系中画出物体在8s内的v- t 图象；（要求计算出相应数值）‎ ‎（3）在8s 内水平力 F 所做的功。‎ ‎（20分）解：（1）（6分）物体受到水平力F和摩擦力f的作用，由静止开始向右做匀加速直线运动，设加速度为a1，4s末速度为v1，由牛顿第二定律： F1-µmg = ma1 （2分）‎ ‎ a1 = 3m/s2 （2分） v1 = at1 = 12m/s （2分）‎ ‎（2）（8分）由图知，4-5s内物体受到水平力F的大小不变，方向改变，设加速度为a2，5s末速度为v2 -(F2+µmg) = ma2 a2 = -7m/ s2 （2分）‎ ‎ v2 = v1 + a2 t2 = 5m/s （2分）‎ 由图知，5-8s内物体只受摩擦力f的作用，设加速度为a3，速度为v3‎ ‎ -µmg = ma3 a3 = -2m/ s2 （1分）‎ ‎ t3 = -=2.5s在t = 7.5s时物体停止运动，v3=0 （1分）‎ 物体运动的v- t 图象如图所示 （2分）‎ ‎（3）（6分）由v- t图可知（或计算得出）‎ ‎ 0-4s内 s1 = 24m （1分）‎ ‎4-5s内 s2 = 8.5 m （1分）‎ 水平力F做功 WF = F1S1-F2S2 （2分） ‎ 解得： WF =155J （2分）‎ F A C B L ‎3．（20分）如图所示，光滑水平地面上停着一辆平板车，其质量为，长为L，车右端（A点）有一块静止的质量为的小金属块．金属块与车间有摩擦，与中点C为界， AC段与CB段动摩擦因数不同．现给车施加一个向右的水平恒力，使车向右运动，同时金属块在车上开始滑动，当金属块滑到中点C时，即撤去这个力．已知撤去力的瞬间，金属块的速度为，车的速度为，最后金属块恰停在车的左端（B点）。如果金属块与车的AC段间的动摩擦因数为，与CB段间的动摩擦因数为，求与的比值．‎ ‎（20分）由于金属块和车的初速度均为零，且经过相等时间加速后车速是金属块速度的2倍，则在此过程中车的加速度是金属块加速度的两倍。‎ 金属块加速度 ① 则车的加速度 ②‎ F A C B L 在此过程中金属块位移 ③ ‎ 车的位移 ④‎ 由位移关系 ⑤ 得 ⑥‎ 从小金属块滑至车中点C开始到小金属块停在车的左端的过程中，系统外力为零，动量守恒，设向右为正方向，且最后共同速度为 ⑦ 得 由能量守恒有 ⑧‎ ‎ 得 ⑨ 由⑥⑨得 ⑩‎ ‎①~⑩每式2分 ‎9.（12分）如图所示，固定在竖直平面内的半径为R的光滑圆环的最高点C处有就一个光滑的小孔，一质量为m的小球套在圆环上，一根细线的一端拴着这个小球，细线的另一端穿过小孔C，手拉细线使小球从A处沿圆环向上移动。在下列两种情况下，当小球通过B处，即∠COB=α=600时，求细线对小球的拉力F的大小和圆环对小球的弹力N的大小。‎ ‎（1）小球沿圆环极缓慢地移动；‎ ‎（2）小球以线速度v沿圆环做匀速圆周运动 解：(1)受力分析如图所示：‎ ‎△COB∽力的矢量三角形 1分 O C B G N T 有 2分 ‎ 1分 解得：N=mg 1分 ‎ 1分 到达底端速度为 ③‎ 在斜面上运动时间 ④‎ 联立解得： ⑤‎ 对B，则有： ⑥‎ 解得 ⑦‎ ‎12. (18分)如图所示，在水平地面上有A、B两个小物体，质量分别为mA＝3.00 kg、mB＝2.00 kg，它们与地面间的动摩擦因数均为μ＝0.1.A、B之间有一原长为L＝15.0 cm、劲度系数为k＝500 N/m的轻质弹簧连接。分别用两个方向相反的水平恒力F1、F2同时作用在A、B两物体上。当运动达到稳定时，A、B两物体以共同加速度大小为a＝1.00 m/s2做匀加速运动。已知F1＝20.0 N，g取10 m/s2。求：运动稳定时A、B之间的距离。‎ 解：(1)当系统具有水平向右的加速度a＝1 m/s2时分析A受力如图：F1－kΔx1－μmAg＝mAa　　(6分)‎ ‎∴Δx1＝＝ m＝2.8×10－2m＝2.8 cm　　(3分)‎ ‎∴L＝L1＋Δx1＝17.8 cm　　(3分)‎ ‎（2）当系统具有水平向左的加速度：a＝1 m/s2时，kΔx2－μmAg－F1＝maa　　(3分)‎ ‎∴Δx2＝＝＝52×10－2m＝5.2 cm　　(3分)‎ ‎∴L＝L＋Δx2＝20.2 cm　　(3分)‎ 注只讨论一种情况且结果正确给12分。‎ ‎【解析】(1)对物体A列牛顿第二定律方程；(2)注意分加速度的方向可能水平向左，也可能水平向右；(3)胡克定律F＝kΔx。‎ A B 地球 同步轨道 图11‎ ‎14、（10分）如图11所示，发射地球同步卫星时，可认为先将卫星发射至距地面高度为h1的圆形近地轨道上，在卫星经过A点时点火（喷气发动机工作）实施变轨进入椭圆轨道，椭圆轨道的近地点为A，远地点为B。在卫星沿椭圆轨道运动到B点（远地点B在同步轨道上）时再次点火实施变轨进入同步轨道，两次点火过程都使卫星沿切向方向加速，并且点火时间很短。已知同步卫星的运动周期为T，地球的半径的R，地球表面重力加速度为g，求：‎ ‎（1）卫星在近地圆形轨道运动时的加速度大小；‎ ‎（2）同步卫星轨道距地面的高度.‎ 解：（1）设地球质量为M，卫星质量为m，万有引力常量为G 卫星在近地轨道圆运动，由万有引力提供向心力得 G =ma （1）‎ 物体在地球表面受到的万有引力等于重力 G = mg （2）‎ 解得a = g ‎（2）设同步轨道距地面高度为h2，由万有引力提供向心力得 G = m(R+h2) （3）‎ 联立（2）（3）得：h2 = － R ‎16、（12分）如图 12 所示，一块质量为M，长为L的均质长木板放在很长的光滑水平桌面上，板的左端有一质量为m的小物体（可视为质点），物体上连接一根很长的细绳，细绳跨过位于桌边的定滑轮．某人以恒定的速率v向下拉绳，物体最多只能到达板的中点，已知整个过程板的右端都不会到达桌边定滑轮处．试求：‎ ‎（1）当物体刚达木板中点时木板的位移；‎ M m v 图 12‎ ‎（2）若木板与桌面之间有摩擦，为使物体能达到板的右端，板与桌面之间的动摩擦因数应满足什么条件？‎ 解：（1）m与M相对滑动过程 ‎ m匀速运动有 : vt = S1 (1)‎ ‎ M匀加速运动有：vt/2 =S2 (2)‎ ‎ S1 - S2 =L/2 (3)‎ ‎ 联立以上三式得S2 = L/2‎ ‎ (2)设m与M之间摩擦因数为μ1‎ ‎ 当桌面光滑时有 mgμ1 = Ma1 （4）‎ ‎ v2 = 2a1S2 (5)‎ ‎ 由（4）（5）得 如果板与桌面有摩擦，因为M与桌面摩擦因数越大，m越易从右端滑下，所以当m滑到M右端两者刚好共速时摩擦因数最小，设为μ2‎ 对M有： (6)‎ ‎ (7)‎ ‎ (8)‎ 对m有： （9）‎ ‎ （10）‎ 联立以上五式得 ‎ 所以桌面与板间的摩擦因数μ ≥ Mv2/2（m + M）gL 。‎ ‎19．（12分）如图所示，M是水平放置的半径足够大的圆盘，绕过其圆心的竖直轴匀速转动，以经过O水平向右的方向作为x轴的正方向．在圆心O正上方距盘面高为h处有一个正在间断滴水的容器，在t＝0时刻开始随传送带沿与x轴平行的方向做匀速直线运动，速度大小为v．已知容器在t＝0时滴下第一滴水，以后每当前一滴水刚好落到盘面上时再滴一滴水．问：‎ ‎（1）每一滴水经多长时间滴落到盘面上？‎ ‎（2）要使每一滴水在盘面上的落点都位于一条直线上，圆盘转动的最小角速度ω．‎ h v x M ‎（3）第二滴水与第三滴水在盘面上的落点间的最大距离 s．‎ ‎（1）水滴在坚直方向作自由落体运动，有 ‎ 得 ‎ ‎（2）要使每一滴水在圆盘面上的落点都位于同一条直线上，在相邻两滴水的下落时间内，圆盘转过的最小角度为π，所以最小角速度为 ‎（3）第二滴水落在圆盘上的水平位移为 第二滴水落在圆盘上的水平位移为 当第二滴水与第三滴水在盘面上的落点位于同一直径上圆心的两侧时两点间的距离最大，为 ‎21．(14分)物理学中库仑定律和万有引力定律有相似的表达形式，对带异种电荷的两粒子组成的系统而言，若定义相距无穷远处电势能为零，则相距为r时系统的电势能可以表示为 ‎。‎ ‎（1）若地球质量为，某人造地球卫星质量为，也定义相距无穷远处引力势能为零，写出当地心与卫星相距R时该系统引力势能表达式。（地球可看作均匀球体，卫星可看成质点）‎ ‎（2）今有一颗卫星贴着地球表面绕行时速度大小为7.90km/s，当该卫星在离地面高度为处绕行时，绕行速度为多大？（R地为地球半径）‎ ‎（3）若在离地面高度为处绕行的卫星质量为1t，则至少需要对该卫星补充多大的能量才能使其脱离地球的束缚？‎ 解析（1）由类比可知，该系统引力势能表达式为：‎ ‎（2）由万有引力提供向心力　 ‎ 得， ‎ 上式中 ‎ 解得km/s ‎ ‎（3）卫星在该处的动能：‎ ‎ ‎ 由 ‎ 系统的势能： ‎ 得系统的机械能： ‎ 则需要给卫星补充的能量： ‎ ‎23．（12分）如图所示是放置在竖直平面内的游戏滑轨，有一质量m=2kg的小球穿在轨道上滑轨由四部分粗细均匀的滑杆组成：水平直轨道AB；倾斜直轨道CD，长L=6m，与水平面间的夹角θ=370；半径R1=1m的圆弧轨道APC；半径R2=3m的圆弧轨道BQED直轨道与圆弧轨道相切，切点分别为A、B、D、C，E为最低点倾斜直轨道CD与小球间的动摩擦因数为μ=2/3，其余部分均为光滑轨道，取g=10m/s2 ,sin370=0.6,cos370=0.8现让小球从AB的正中央以初速度V0=10m/s开始向左运动，问：‎ ‎（1）第一次经过E处时，轨道对小球的作用力为多大？‎ ‎（2）小球第一次回到出发点时的速度为多大？‎ ‎（3）小球在运动过程中，损失的机械能最多为多少?‎ ‎25．（18分）下图中，轻弹簧的一端固定，另一端与滑块B相连，B静止在水平导轨上，弹簧处在原长状态。另一质量与B相同滑块A，从导轨上的P点以某一初速度向B滑行，当A滑过距离时，与B相碰，碰撞时间极短，碰后A、B紧贴在一起运动，但互不粘连。已知最后A恰好返回出发点P并停止。滑块A和B与导轨的滑动摩擦因数都为，运动过程中弹簧最大形变量为，求A从P出发时的初速度。‎ 设A、B质量皆为m，A刚接触B时速度为（碰前），由动能关系，有 ‎ ①‎ ‎ A、B碰撞过程中动量守恒，令碰后A、B共同运动的速度为有 ‎ ②‎ 碰后A、B先一起向左运动，接着A、B一起被弹回，在弹簧恢复到原长时，设A、B的共同速度为，在这过程中，弹簧势能始末两态都为零，利用动能定理，有 ‎ ③‎ 此后A、B开始分离，A单独向右滑到P点停下，由动能定理有 ‎ ④‎ 由以上各式，解得 ⑤‎ ‎26．（19分）如图14所示，在同一竖直上，质量为2m的小球A静止在光滑斜面的底部，斜面高度为H=2L。小球受到弹簧的弹性力作用后，沿斜面向上运动。离开斜面后，运动到最高点时与静止悬挂在此处的小球B发生碰撞（碰撞过程无动能损失）；碰撞后球B刚好能摆到与悬点O同一高度，球A沿水平方向抛射落在水平面C上的P点，O点的投影O＇与P的距离为L/2。已知球B质量为m，悬绳长L，视两球为质点，重力加速度为g，不计空气阻力，求：‎ ‎（1）球A在两球碰撞后一瞬间的速度大小；‎ ‎（2）碰后在球B摆动过程中悬绳中的最大拉力； ‎ ‎（3）弹簧的弹性力对球A所做的功。‎ ‎（1）设碰撞后的一瞬间，球B的速度为vB/，由于球B恰好与悬点O同一高度，根据动能定理：‎ ‎ ①‎ ‎ ②‎ 球A达到最高点时，只有水平方向速度，与球B发生弹性碰撞.设碰撞前的一瞬间，球A水平方向速度为vx.碰撞后的一瞬间，球A速度为vx/.‎ 球A、B系统碰撞过程中水平方向动量守恒、机械能守恒：‎ ‎ ③‎ ‎ ④‎ 由②③④解得： ⑤‎ ‎ ⑥‎ 故，.碰撞后的一瞬间，球A速度为 ‎ ‎（2） 球A在摆动过程中，在最低点绳的拉力最大，由牛顿定律：‎ ‎ T-mg=m V’B V’B//L.‎ ‎ 所以 T=‎ ‎（3）碰后球A作平抛运动.设从抛出到落地时间为t，平抛高度为y，则：‎ ‎ ⑦‎ ‎ ⑧‎ 由⑤⑦⑧得：y=L 以球A为研究对象，弹簧的弹性力所做的功为W，从静止位置运动到最高点：‎ ‎⑨‎ 由⑤⑥⑦得：‎ W=mgL ‎ ‎28. (18分) 如图所示，质量为m=10kg的两个相同的物块A、B(它们之间用轻绳相连)放在水平地面上，在方向与水平方面成角斜向上、大小为100N的拉力F作用下，以大小为=4． 0m／s的速度向右做匀速直线运动，求剪断轻绳后物块A在水平地面上滑行的距离。(取当地 的重力加速度g=10m/s2，sin37=0．6，cos37=0．8)‎ 解析：设两物体与地面间的动摩擦因素为，根据滑动摩擦力公式和平衡条件，对A、B整体有：‎ ‎ ①‎ ‎ 剪断轻绳以后，设物体A在水平地面上滑行的距离为s，有 ‎ ②‎ ‎ ③‎ ‎ 联解方程，代人数据得： m ‎29.(20分) 一卡车拖挂一相同质量的车厢，在水平直道上以的速度匀速行驶，其所受阻力可视为与车重成正比，与速度无关。某时刻，车厢脱落，并以大小为的加速度减速滑行。在车厢脱落后，司机才发觉并紧急刹车，刹车时阻力为正常行驶时的3倍。假设刹车前牵引力不变，求卡车和车厢都停下后两者之间的距离。‎ 解：设卡车的质量为M，车所受阻力与车重之比为；刹车前卡车牵引力的大小为，‎ 卡车刹车前后加速度的大小分别为和。重力加速度大小为g。由牛顿第二定律有 设车厢脱落后，内卡车行驶的路程为，末速度为，根据运动学公式有 ‎ ⑤‎ ‎ ⑥‎ ‎ ⑦‎ 式中，是卡车在刹车后减速行驶的路程。设车厢脱落后滑行的路程为 有 ⑧‎ 卡车和车厢都停下来后相距 ⑨‎ 由①至⑨式得 ⑾‎ 带入题给数据得 　⑿‎ υ0‎ h ‎53°‎ s H L B A m ω ‎24．（18分）如图所示，顺时针以4.0m/s匀速转动的水平传送带的两个皮带轮的圆心分别为A、B，右端与等高的光滑水平平台恰好接触。一小物块m（可看成质点）从A点正上方轻放于传送带上，小物块与传送 带间动摩擦因数μ=0.3，最后从光滑水平平台上滑出，恰好落在临近平台的一倾角为 α = 53°的光滑斜面顶端，并刚好沿光滑斜面下滑，已知斜面顶端与平台的高度差h=0.8m，g = 10m/s2，sin53° = 0.8，cos53° = 0.6，则 ‎ （1）小物块水平抛出的初速度v0是多少？‎ ‎（2）斜面顶端与平台右边缘的水平距离s和传送带AB长度L各是多少？‎ ‎ （3）若斜面顶端高H = 20.8m，则小物块离开平台后经多长时间t到达斜面底端？‎ 解：（1）由题意可知：小块落到斜面上并沿斜面下滑，说明此时小块速度方向与斜面平行，否则小块会弹起，所以vy = v0tan53° （2分）‎ ‎ vy2 = 2gh （2分）‎ 代入数据，得vy = 4m/s，v0 = 3m/s （2分）‎ ‎（2）由vy = gt1得t1 = 0.4s （1分）‎ s =v0t1 = 3×0.4m = 1.2m （1分）‎ 因为物块离开传送带的速度小于4.0m/s，所以一直匀加速 由得：=1.5m ‎（3）小块沿斜面做匀加速直线运动的加速度a = （2分）‎ 初速度 = 5m/s （2分）‎ mg ma T mg ‎ =vt2 + a t22 （2分）‎ 代入数据，整理得 4t22 + 5t2 - 26 = 0‎ 解得 t2 = 2s 或t2 = - 13s（不合题意舍去） （1分）‎ 所以t = t1 + t2 = 2.4s （1分 ‎25．（19分）如图甲所示，将质量为m的两个小球（可看成质点），用长为L的两根细软线拴连，线的上端连于O点且绕O点自由转动时与竖直方向夹角为θ。‎ 如图乙所示，将其中一质量为m的小球仍与一长为L的细绳连接，放在表面光滑的正圆锥体表面，上端可绕圆锥顶点自由转动。圆锥体放在水平面上，其轴线沿竖直方向，圆锥母线与轴线之间夹角α为30°，试求：‎ ‎（1）图甲中小球圆周运动的周期T=？‎ ‎（2）图乙中当正圆锥体沿水平x轴方向匀加速运动的加速度a多大时，小球刚要离开锥面？‎ ‎（3）将图乙中与小球相连的细线穿过圆锥顶端的光滑小圆环后,与放在倾角β=37°的对称斜槽（斜槽两平面材料相同，与竖直面都成30°）里的质量为M的圆柱体相连，连接圆 柱的细线平行斜槽的棱，如图丙所示。当小球以速度v=绕圆锥轴线做水平匀速圆周运动而圆柱M不动时，圆柱与两接触面间的摩擦因数μ至少多大？‎ L α m x y β ‎60°‎ L α m x y L 图甲 L O θ θ 图乙 图丙 解:（1）对甲图中小球由向心力公式: ‎ 得: ‎ ‎（2）对乙图中小球，由牛顿定律得: ‎ 所以:‎ ‎（3）设小球刚好飞起的临界速度为v0，由（2）可得：‎ ‎，则 因＞，所以小球已经飞离锥面。设细线与水平方向成γ角。‎ Tcosγ T mg γ Tsinγ 则有： ‎ 可得：‎ ‎60°‎ Mg ‎4‎ ‎5‎ N N ‎120°‎ ‎120°‎ ‎120°‎ 垂直圆柱端面看：圆柱受力如图所示：两支持力N对称大小相等，且与重力Mg的垂直 棱的分力Mgcos37°互成120°，则有：‎ 由不滑动的条件有：‎ 所以：‎