北京高考理科数学2018模拟试题1含答案详细评标及试题难度系数分析

北京高考理科数学2018模拟试题1含答案详细评标及试题难度系数分析

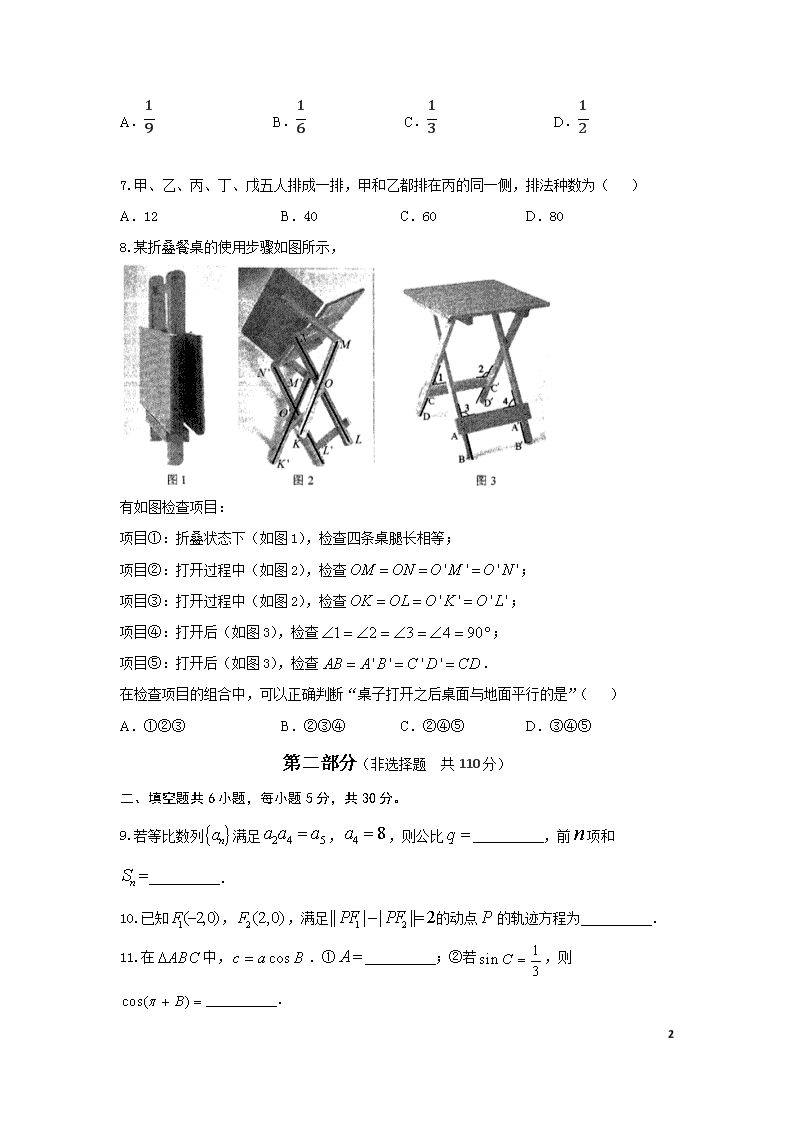
注：1-4页为试题，5-11页为详细答案及评分标准，12-13页为试题难度说明.‎ ‎ 本试卷配套标准答题纸可在百度文库本试卷作者处免费获得.‎ 印发时，请删去本标注.‎ 普通高等学校招生全国统一考试模拟试卷1（北京卷）‎ 理科数学 本试卷共4页，150分。考试时长120分钟，考生务必将答案填写在答题卡上，在试卷上作答无效。考试结束后，将本试卷、答题卡和草稿纸一并收回。‎ 第一部分（选择题 共40分）‎ 一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ ‎1.已知集合，，若 A． B． C． D．‎ ‎2.下列函数中，在区间上为增函数的是 A． B． C． D．‎ ‎3.设是公比为q的等比数列，则“”是“为递增数列”的 A．充分且不必要条件 B．必要且不充分条件 C．充分且必要条件 D．既非充分也非必要条件 ‎4.设，，若，则 A． B． C． D．‎ ‎5.若输出的的值为64，则判断框内应填入的条件是 A. B. C. D.‎ ‎6．某三棱锥的三视图如图所示，则该三棱锥的体积为 ‎ 13‎ A．‎1‎‎9‎ B．‎1‎‎6‎ C．‎1‎‎3‎ D．‎1‎‎2‎ ‎ ‎7.甲、乙、丙、丁、戊五人排成一排，甲和乙都排在丙的同一侧，排法种数为（ ）‎ A．12 B．40 C．60 D．80 ‎ ‎8.某折叠餐桌的使用步骤如图所示，‎ 有如图检查项目：‎ 项目①：折叠状态下（如图1），检查四条桌腿长相等；‎ 项目②：打开过程中（如图2），检查；‎ 项目③：打开过程中（如图2），检查；‎ 项目④：打开后（如图3），检查；‎ 项目⑤：打开后（如图3），检查．‎ 在检查项目的组合中，可以正确判断“桌子打开之后桌面与地面平行的是”（ ）‎ A．①②③ B．②③④ C．②④⑤ D．③④⑤ ‎ 第二部分（非选择题 共110分）‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎9.若等比数列满足，，则公比 ，前项和 ．‎ ‎10.已知，，满足的动点的轨迹方程为 ．‎ ‎11.在中，．① ；②若，则 ．‎ ‎ 13‎ ‎12.若非零向量，满足，，则向量，夹角的大小为 ．‎ ‎13.已知函数若关于的方程在内有唯一实根，则实数的最小值是 ．‎ ‎14.已知实数，，，满足，则的最大值是 ．‎ 三、解答题共6小题，共80分。‎ ‎15.（本小题13分）如图，在中，，，点D在BC边上，且CD=2，‎ ‎.‎ ‎（Ⅰ）求．‎ ‎（Ⅱ）求，的长．‎ ‎16.（本小题13分）‎ 某公司购买了A,B,C三种不同品牌的电动智能送风口罩.为了了解三种品牌的口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试他们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：‎ A ‎4 4.5 5 5.5 6 6‎ B ‎4.5 5 6 6.5 6.5 7 7 7.5‎ C ‎5 5 5.5 6 6 7 7 7.5 8 8 9‎ ‎（Ⅰ）已知该公司购买的C品牌电动智能送风口罩比B品牌多150台，求该公司购买的B品牌电动智能送风口罩的数量；‎ ‎（Ⅱ）从A品牌和B品牌抽出的电动智能送风口罩中，各随机选取一台，求A品牌待机时长高于B品牌的概率；‎ ‎（Ⅲ）从A品牌的电动智能送风口罩中, 随机选取2台，其中待机时长 ‎ 13‎ 不高于4.5小时的为X台，求X的分布列和数学期望.‎ ‎17. （本小题14分）如图，由直三棱柱和四棱锥构成的几何体中，，，，，平面平面．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）若为的中点，求证：平面；‎ ‎（Ⅲ）在线段上是否存在点，使直线与平面所成的角为？若存在，求的值，若不存在，说明理由．‎ ‎18. （本小题13分）‎ ‎ 已知函数．‎ ‎（Ⅰ）求曲线在点处的切线方程；‎ ‎（Ⅱ）求证：当时，；‎ ‎（Ⅲ）设实数使得对恒成立，求的最大值．‎ ‎19. （本小题14分）已知椭圆：，与轴不重合的直线经过左焦点，且与椭圆相交于，两点，弦的中点为，直线与椭圆相交于，两点．‎ ‎（Ⅰ）若直线的斜率为1，求直线的斜率；‎ ‎（Ⅱ）是否存在直线，使得成立？若存在，求出直线的方程；若不存在，请说明理由．‎ ‎20.（本小题13分）已知含个元素的正整数集（，）具有性质：对任意不大于（其中）的正整数，存在数集的一个子集，使得该子集所有元素的和等于．‎ ‎（Ⅰ）写出，的值；‎ ‎（Ⅱ）证明：“，，…，成等差数列”的充要条件是“”；‎ ‎ 13‎ ‎（Ⅲ）若，求当取最小值时的最大值．‎ 普通高等学校招生全国统一考试模拟试卷1（北京卷）‎ 理科数学 参考答案 一、选择题（共8小题，每小题5分，共40分）‎ ‎（1）C （2）A （3）D （4）C ‎（5）A （6）B （7）D （8）B 二、填空题（共6小题，每小题5分，共30分）‎ ‎9.2， 10. 11.π‎2‎， 12.‎2π‎3‎ 13. 14.‎ 三、选择题（共6小题，共80分）‎ ‎15.（共13分）‎ 解：（I）在中，因为，所以。……….…2‎ 所以 ‎…………………….……6‎ ‎（Ⅱ）在中，由正弦定理得 ‎，…………………………………………9‎ 在中，由余弦定理得 所以…………………………………………………………..……………………13‎ ‎ 13‎ ‎16.（本小题共13分） ‎ 解：（Ⅰ）设该公司购买的B品牌电动智能送风口罩的数量为x台. ………………….0‎ 则购买的C品牌电动智能送风口罩为‎11‎‎8‎x台 ……………………………………………1‎ 由题意得：‎11‎‎8‎x – x =150.所以x = 400. …………………………………………………..2‎ 答：该公司购买的B品牌电动智能送风口罩的数量为400台. ……………………...…3‎ ‎（Ⅱ）设A品牌待机时长高于B 品牌的概率为P 则P = ‎7‎‎6×8‎ =‎ ‎‎7‎‎48‎ ………………………………………………………………..……..5‎ 答：A品牌待机时长高于B 品牌的概率为‎7‎‎48‎. ………………………………………..6‎ ‎（Ⅲ）X可能的取值为0,1,2 …………………………………………………….7‎ P（X=0）= C‎4‎‎2‎C‎6‎‎2‎ = ‎2‎‎5‎ ……………………………………………………8‎ P（X=1）= C‎2‎‎1‎C‎4‎‎1‎C‎6‎‎2‎ = ‎8‎‎15‎ ……………………………………………………9‎ P（X=1）= ‎1‎C‎6‎‎2‎ = ‎1‎‎15‎ ……………………………………………………10‎ 则X的分布列为： ……………………………………11‎ X ‎0‎ ‎1‎ ‎2‎ P ‎2‎‎5‎ ‎8‎‎15‎ ‎1‎‎15‎ 则X的数学期望为：E(X) = 0‎×‎2‎‎5‎ ‎+ 1‎×‎8‎‎15‎+2× ‎1‎‎15‎ ‎=‎ ‎‎2‎‎3‎ ……………………………13‎ ‎17.（Ⅰ）证明：在直三棱柱中，平面，‎ 故，‎ 由平面平面，且平面平面，‎ 所以平面，……………………….. ……………………….. …………..2‎ 又平面，……………………….. ……………………….. …………....3‎ ‎ 13‎ 所以．………………………..……………………………………..………4‎ ‎（Ⅱ）证明：在直三棱柱中，平面，‎ 所以，，‎ 又，‎ 所以，如图建立空间直角坐标系，……………………….. ………………..5‎ 依据已知条件可得，，，，，，‎ 所以，，……………………….. ……………….…..6‎ 设平面的法向量为，‎ 由……………………….. ……………….….. ………………………….7‎ 即 令，则，，于是，‎ 因为为中点，所以，所以，……………..8‎ 由，可得，……………….………...9‎ 所以与平面所成角为0，‎ 即平面．……………….……………………….……………………..10‎ ‎ 13‎ ‎（Ⅲ）解：由（Ⅱ）可知平面的法向量为．‎ 设，，………….……………………….……………………..11‎ 则，．….…………………..…..12‎ 若直线与平面成角为，则 ‎，…………………..…..13‎ 解得，‎ 故不存在这样的点．…………………..…. …………………..…. ………………...14‎ ‎18. 解：（I）因为=ln（1+x）-ln（1-x），所以 ‎ =，=2. ………………..…. ……………….....2‎ ‎ 又因为=0，所以曲线y= 在点（0 ，）处的切线方程为y=2x.‎ ‎………………..…. ………………..... ………………..…. ………………..................4‎ ‎ （Ⅱ）令=-2(x+)，则 ‎ =-2（1+）=.……………..…. ……………….....6‎ ‎ 因为>0（0=0，x∈（0，1），………..…. ……………….........7‎ ‎ 即当x∈（0，1）时，>2(x+).……..…. ………………........8‎ ‎（Ⅲ）由（Ⅱ）知，当k《2时，>k(x+)对x∈（0，1）恒成立.‎ ‎ 当k>2时，令=- k(x+)，则 ‎ =-k（1+）=.……..…. ……………….........10‎ ‎ 所以当时，<0，因此在区间（0，）上单调递减.‎ ‎ 当时，<=0，即< k(x+).‎ ‎ 所以当K>2时，> k(x+)并非对x∈（0，1）恒成立.‎ ‎ 13‎ ‎ 综上可知，k的最大值为2。…….........….........….........….........…….....13‎ ‎19.解：（Ⅰ）由已知可知，又直线的斜率为1，所以直线的方程为，‎ 设，，…….........….... …….........….... …….........…...............1‎ 由解得…….........….... …….........…...............2‎ 所以中点，…….........….... …….........…............... …….........….3‎ 于是直线的斜率为．..….... …….........…............... …….........…4‎ ‎（Ⅱ）假设存在直线，使得成立．　‎ 当直线的斜率不存在时，的中点，‎ 所以，，矛盾；. …….........6‎ 故可设直线的方程为，联立椭圆的方程，‎ 得，‎ 设，，则，，..........7‎ 于是，‎ 点的坐标为，.......... .......... .......... .......... .......... ..........9‎ ‎.‎ ‎........ .......... .......... .......... .......... ... ........ .......... .......... .......... .......... ... ........ ........10‎ ‎ 13‎ 直线的方程为，联立椭圆的方程，得，‎ 设，则，....... ............11‎ 由题知，，‎ 即，....... ........ ....... ........ ....... ........ ...12‎ 化简，得，故，.. ..... ..... ..... ........... ....... ........ ....... ........ ...13‎ 所以直线的方程为，.. ........ ....... ........ .....14‎ 阅卷说明：第13、14分若少一种情况，可得一分.‎ ‎20.解：（Ⅰ），. ........ ....... ........ . ........ ....... ........ . ........ ....... ..3‎ ‎（Ⅱ）先证必要性：‎ 因为，，又，，…，成等差数列，... ........ . ........ .......4‎ 故，所以；.... ........ . ........ ....... ........ . ........ ..............5‎ 再证充分性：‎ 因为，，，…，为正整数数列，故有 ‎，， ，，…，，‎ 所以，.... . ........ ...........6‎ 又，故（，，…，），故，，…，为等差数列．.... . ........ .......... .... . ........ .......... .... . ........ .......... .... . ........ .......... .... . ....8‎ ‎（Ⅲ）先证明（，，…，）．‎ 假设存在，且为最小的正整数．.. .......... .... . ........ .......... ..... . 9‎ 依题意，则，，又因为 ‎ 13‎ ‎，‎ 故当时，不能等于集合的任何一个子集所有元素的和．‎ 故假设不成立，即（，，…，）成立．... .......... .....10‎ 因此，‎ 即，所以．　.. .......... ..... .. .......... ..... .. .......... ..... .. ........11‎ 因为，则，‎ 若时，则当时，集合中不可能存在若干不同元素的和为，‎ 故，即... .......... ..... .. .......... ..... …................12‎ 此时可构造集合.‎ 因为当时，可以等于集合中若干个元素的和；‎ 故当时，可以等于集合中若干不同元素的和；‎ ‎……‎ 故当时，可以等于集合中若干不同元素的和；‎ 故当时，可以等于集合中若干不同元素的和；‎ 故当时，可以等于集合中若干不同元素的和，‎ 所以集合满足题设，‎ 所以当取最小值11时，的最大值为．. .......... ..... …................13‎ 阅卷说明：第（Ⅲ）问，可根据实际情况调整给分.‎ ‎ 13‎ 普通高等学校招生全国统一考试模拟试卷1（北京卷）‎ 理科数学 试题难度说明 一、整体难度：0.75‎ 根据本评分标准，预估平均分：112. ‎ 二、各题难度：‎ ‎1. 难度系数：0.95；知识点：集合. ‎ ‎2. 难度系数：0.88；知识点：函数基础，基本初等函数，初等函数.‎ ‎3. 难度系数：0.73；知识点：充分必要条件，等比数列.‎ ‎4. 难度系数：0.75；知识点：不等式，基本初等函数，初等函数，函数思想.‎ ‎5. 难度系数：0.81；知识点：算法与逻辑.‎ ‎6. 难度系数：0.82；知识点：空间几何体三视图，棱锥的体积计算.‎ ‎7. 难度系数：0.78；知识点：计数原理.‎ ‎8. 难度系数：0.50；知识点：空间几何体的条件推理，联系实际解决问题.‎ ‎9. 难度系数：0.90；知识点：等比数列.‎ ‎10.难度系数：0.87；知识点：动点轨迹拟合.‎ ‎11.难度系数：0.91；知识点：解三角形，诱导公式.‎ ‎12.难度系数：0.73；知识点：平面向量.‎ ‎13.难度系数：0.65；知识点：初等函数.‎ ‎14.难度系数：0.41；知识点：线性规划.‎ ‎15.难度系数：0.72；知识点：三角函数，解三角形.‎ ‎16.难度系数：0.88；知识点：统计与概率，分布列与期望.‎ ‎17.难度系数：0.87；知识点：空间几何体元素关系，空间向量.‎ ‎18.难度系数：0.70；知识点：导数，不等式的解法，初等函数的性质.‎ ‎19.难度系数：0.62；知识点：解析几何中椭圆与直线的方程，平面几何技巧.‎ ‎20.难度系数：0.48；知识点：集合，不等式，逻辑及语言，数列.‎ ‎ 13‎ 三、考察能力及对应高考考试方向：‎ 本试卷考察学生的基础知识，及运用基础知识解决问题的能力，并在此过程中，运用部分解决问题的技巧.这些技巧要求不高，是学生在日常解决问题中经过思考可以具备的.‎ 例如：‎ 第8 题，考察学生对于立体几何体的整体感知能力和自设自证的能力.当然，对于空间想象和空间证明比较清楚的学生，可以不需要自设自证的过程，即可推理出正确选项.‎ 第13题，考察学生的函数作图，及最基本的平移变换的能力。学生只需抓住a的变化给函数图像带来的变化即可.‎ 第14题，首先考察学生的线性规划作图能力，在图示作好后，需重点关注“”这个条件.程度较高的学生会反应出几组满足条件的u和v的值，代入值尝试几次即可迅速得到答案.‎ 第15题，本题较以往的三角函数题目有所不同.对于正余弦定理不熟悉的学生，较难找到标答这样的简便做法，但经过尝试基本可以将本题完成..本题意在拖延时间，但不是以复杂，而是通过思维链长度及做法选择上增大难度，锻炼学生在考场做题时，遇到难题不慌不乱，从容完成接下来的题目.‎ 第19题，第（Ⅱ）问，在计算M点坐标之前的部分大多数学生可以完成，但是在对于这一问中“”条件的处理不够充分.这一条件有两方面需要处理AM和CM、DM与OM的联系，以简化计算。‎ 第20题，考察学生基本价值判断和逻辑判断，考察形式比较常规，此处不再赘述.‎ 以上列举了本试卷中比较典型的考察学生解题能力和技巧的题目，其中的叙述仅做参考.在5-11页的评分标准中所列的给分办法，都是根据上一年高考情况拟定，正式高考评卷时可能会在部分题目的评分标准中做出调整，以保证分数合理化，最大程度地反应学生真实的水平及学生之间的差距.‎ ‎ 2018.05.11‎ ‎ 13‎