- 2021-05-13 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017年高考模拟试卷(4)
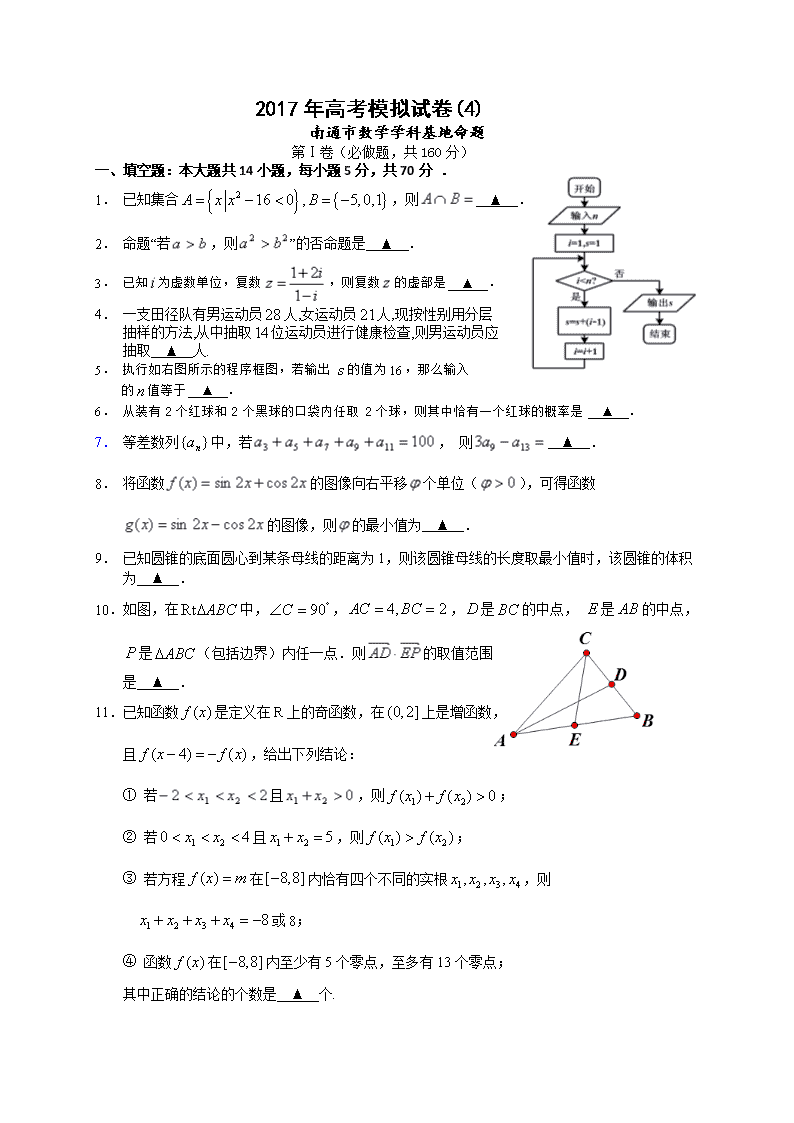
2017年高考模拟试卷(4) 南通市数学学科基地命题 第Ⅰ卷(必做题,共160分) 一、填空题:本大题共14小题,每小题5分,共70分 . 1. 已知集合,则 ▲ . 2. 命题“若,则”的否命题是 ▲ . 3. 已知为虚数单位,复数,则复数的虚部是 ▲ . 4. 一支田径队有男运动员人,女运动员人,现按性别用分层 抽样的方法,从中抽取位运动员进行健康检查,则男运动员应 抽取 ▲ 人. 5. 执行如右图所示的程序框图,若输出的值为16,那么输入 的值等于 ▲ . 6. 从装有2个红球和2个黑球的口袋内任取2个球,则其中恰有一个红球的概率是 ▲ . 7. 等差数列中,若, 则 ▲ . 8. 将函数的图像向右平移个单位(),可得函数 的图像,则的最小值为 ▲ . 9. 已知圆锥的底面圆心到某条母线的距离为1,则该圆锥母线的长度取最小值时,该圆锥的体积 为 ▲ . 10.如图,在中,,,是的中点, 是的中点, 是(包括边界)内任一点.则的取值范围 是 ▲ . 11.已知函数是定义在R上的奇函数,在上是增函数, 且,给出下列结论: ① 若且,则; ② 若且,则; ③ 若方程在内恰有四个不同的实根,则 或8; ④ 函数在内至少有5个零点,至多有13个零点; 其中正确的结论的个数是 ▲ 个. 12.已知函数满足,当时,,若在区间上, 函数恰有一个零点,则实数的取值范围是 ▲ . 13.设P是圆M:(x-5)2+(y-5)2=1上的动点,它关于A(9,0)的对称点为Q,把P绕原点依逆时针 方向旋转90°到点S,则|SQ|的取值范围为 ▲ . 14.如图,在数轴上截取与闭区间对应的线段,对折后(坐标4所对应的点与原点重合)再 均匀地拉成4个单位长度的线段,这一过程称为一次操作(例如在第一次操作完成后,原来的 坐标1、3变成2,原来的坐标2变成4,等等).那么原闭区间上(除两个端点外)的点, 在第次操作完成后(),恰好被拉到与4重合的点所对应的坐标组成的集合是 ▲ . 2 4 (14题图) 二、解答题:本大题共6小题,共90分. 15.(本小题满分14分) 在中,角,,所对的边分别为,,,,. (1)求及的值; (2)若,求的面积. 16.(本小题满分14分) 如图所示,在三棱柱中,为正方形,为菱形,, 平面平面. (1)求证:; (2)设点分别是的中点,试判断直线与平面的位置关系,并说明理由; 17.(本小题满分14分) 已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用,其 标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数, 根据实际剩余配料的重量,以每天0.03元/千克支付.高考资源网 (1)当9天购买一次配料时,求该厂用于配料的保管费用P是多少元?高考资源网 (2)设该厂天购买一次配料,求该厂在这天中用于配料的总费用(元)关于的函数 关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?高考 18.(本小题满分14分) 已知椭圆的离心率为,短轴端点到焦点的距离为2. (1)求椭圆C的方程; (2)设点A,B是椭圆C上的任意两点, O是坐标原点,且OA⊥OB; ① 求证:存在一个定圆,使得直线AB始终为该定圆的切线,并求出该定圆的方程; ② 若点O为坐标原点,求面积的最大值. 19.(本小题满分16分) 已知曲线 ,过上一点作一斜率的直线交曲线C 于另一点, . (1)求与之间的关系式; (2)求证:数列是等比数列,并求数列的通项公式; (3)求证: 20.(本小题满分16分) 已知函数(). (1)当时,求函数的单调区间; (2)若函数既有一个极小值和又有一个极大值,求的取值范围; (3)若存在,使得当时,的值域是,求的取值范围. 注:自然对数的底数. 第II卷(附加题,共40分) 21.【选做题】本题包括A, B,C,D四小题,每小题10分,请选定其中两小题,并在相应的答题区域内作答. A,(选修4-1;几何证明选讲) 如图,已知切圆于点,是圆的直径,交圆于点,是圆的切线, 于,,求的长. B.(选修4-2:矩阵与变换)求将曲线绕原点逆时针旋转后所得的曲线方程. C.(选修4-4:坐标系与参数方程)已知极坐标系的极点与直角坐标系的原点重合,极轴与轴的 非负半轴重合.若曲线的方程为,曲线的参数方程为 (1) 将的方程化为直角坐标方程; (2)若点为上的动点,为上的动点,求的最小值. D.(选修4-5:不等式选讲)设函数 (1)求不等式的解集; (2)若恒成立,求实数的取值范围. 【选做题】第22题、23题,每题10分,共计20分. 22.设A,B是治疗同一种疾病的两种药,用若干试验组进行对比试验.每个试验组由4只小白鼠 组成,其中2只服用A,另2只服用B,然后观察疗效.若在一个试验组中,服用A有效的小 白鼠的只数比服用B有效的只数多,就称该试验组为甲类组.设每只小白鼠服用A有效的概率 为,服用B有效的概率为. (1)求一个试验组为甲类组的概率; (2)观察三个试验组,用X表示这三个试验组中甲类组的个数,求X的分布列和数学期望. 23.用数学归纳法证明:,其中 2017年高考模拟试卷(4)参考答案 一、填空题 1. .∵A={x|-4查看更多