备战2020年高考数学大一轮复习 热点聚焦与扩展 专题27 向量的数量积——数量积的投影定义

备战2020年高考数学大一轮复习 热点聚焦与扩展 专题27 向量的数量积——数量积的投影定义

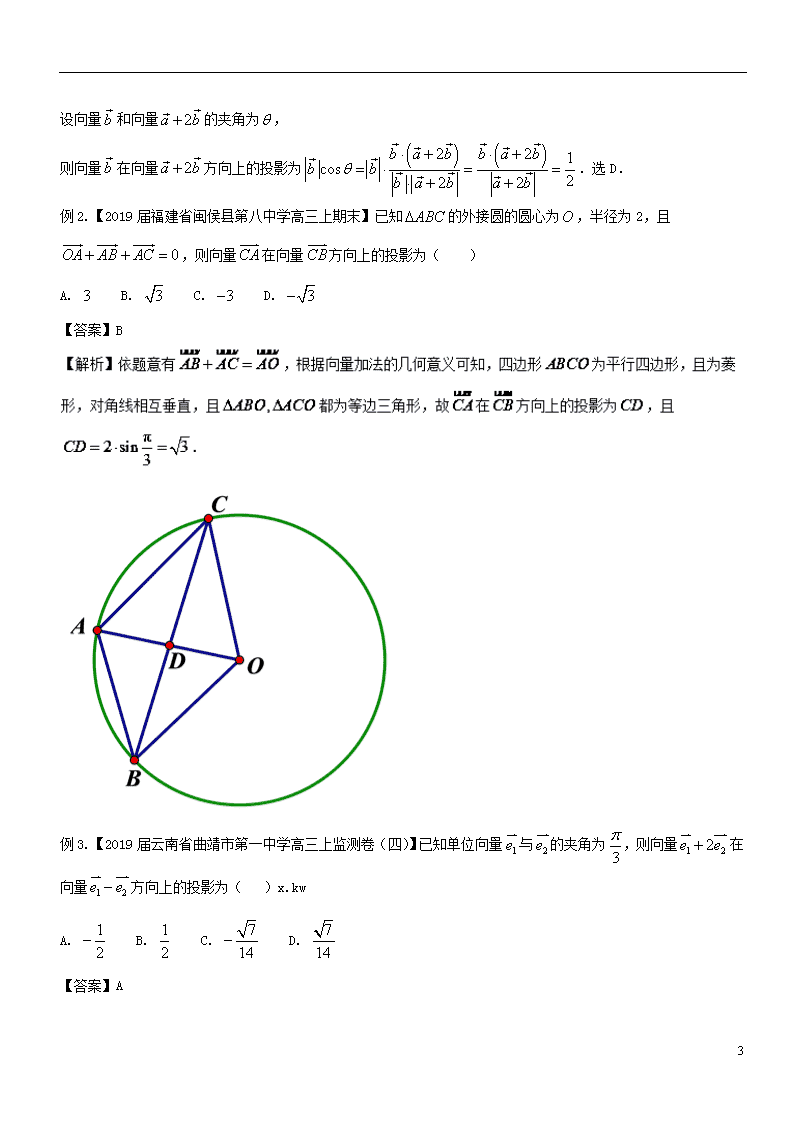
专题27 向量的数量积——数量积的投影定义 ‎【热点聚焦与扩展】‎ 平面向量的数量积是高考考查的重点、热点，往往以选择题或填空题的形式出现.常常以平面图形为载体，借助于向量的坐标形式等考查数量积、夹角、垂直的条件等问题；也易同三角函数、解析几何等知识相结合，以工具的形式出现．‎ ‎1、向量的投影：‎ ‎（1）有向线段的值：设有一轴，是轴上的有向线段，如果实数满足，且当与轴同向时，，当与轴反向时，，则称为轴上有向线段的值.‎ ‎（2）点在直线上的投影：若点在直线外，则过作于，则称为在直线上的投影；若点在直线上，则在在直线上的投影与重合.所以说，投影往往伴随着垂直.‎ ‎（3）向量的投影：已知向量，若的起点在所在轴（与同向）上的投影分别为，则向量在轴上的值称为在上的投影，向量称为在上的投影向量.‎ ‎2、向量的投影与向量夹角的关系：通过作图可以观察到，向量的夹角将决定投影的符号，记为向量的夹角 ‎（1）为锐角：则投影（无论是在上的投影还是在上的投影）均为正 ‎（2）为直角：则投影为零 ‎（3）为钝角：则投影为负 ‎3、投影的计算公式：以在上的投影为例，通过构造直角三角形可以发现 ‎（1）当为锐角时，，因为，所以 ‎（2）当为锐角时，，因为，所以即 ‎（3）当为直角时，，而，所以也符合 13‎ 综上可得：在上的投影，即被投影向量的模乘以两向量的夹角 ‎4、数量积与投影的关系（数量积的几何定义）：‎ 向量数量积公式为，可变形为或，进而与向量投影找到联系 ‎ ‎（1）数量积的投影定义：向量的数量积等于其中一个向量的模长乘以另一个向量在该向量上的投影，即（记为在上的投影）‎ ‎（2）投影的计算公式：由数量积的投影定义出发可知投影也可利用数量积和模长进行求解：‎ ‎ 即数量积除以被投影向量的模长 ‎5、数量积投影定义的适用范围：作为数量积的几何定义，通常适用于处理几何图形中的向量问题 ‎（1）图形中出现与所求数量积相关的垂直条件，尤其是垂足确定的情况下（此时便于确定投影），例如：直角三角形，菱形对角线，三角形的外心（外心到三边投影为三边中点）‎ ‎（2）从模长角度出发，在求数量积的范围中，如果所求数量积中的向量中有一个模长是定值，则可以考虑利用投影，从而将问题转化为寻找投影最大最小的问题 ‎【经典例题】‎ 例1.【2019届江西省重点中学协作体高三下学期第一次联考】设向量， 满足， ，且，则向量在向量方向上的投影为（ ）‎ A. B. C. D. ‎ ‎【答案】D 13‎ 设向量和向量的夹角为，‎ 则向量在向量方向上的投影为．选D．‎ 例2.【2019届福建省闽侯县第八中学高三上期末】已知的外接圆的圆心为，半径为2，且，则向量在向量方向上的投影为（ ）‎ A. B. C. D. ‎ ‎【答案】B 例3.【2019届云南省曲靖市第一中学高三上监测卷（四）】已知单位向量与的夹角为，则向量在向量方向上的投影为（ ）x.kw ‎ A. B. C. D. ‎ ‎【答案】A 13‎ ‎【解析】∵单位向量与的夹角为 ‎∴‎ ‎∴，‎ ‎∴ 向量在向量方向上的投影为： ，故选A.‎ 例4.设， ， ，且，则在上的投影的取值范围( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由题意可知 当 故当时， 取得最小值为，即 当时， ，即 13‎ 综上所述 故答案选 点睛：由已知求得及，代入投影公式，对分类后利用二次函数求最值，在分类讨论时需要讨论完整，不要漏掉哪种情况，讨论完可以检查下是否把整个实数全部取完.‎ 例5.如图，菱形的边长为为中点，若为菱形内任意一点（含边界），则的最大值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎ ‎ 答案D.‎ ‎【名师点睛】（1）从本例也可以看出投影计算数量积的一个妙用，即在求数量积最值时，如果其中一个向量位置确定，那么只需看另一向量在该向量处的投影即可，这种方法往往能够迅速找到取得最值的情况 ‎（2）在找到取到最值的点位置后，发现利用投影计算数量积并不方便（投影，不便于计算），则要灵活利用其他方法把数量积计算出来（寻求基底，建系等）.正所谓：寻找最值用投影，而计算时却有更多方法供选择.‎ 13‎ 例6.【2019届衡水金卷四】已知平面向量，，且，则在方向上的投影是__________．‎ ‎【答案】‎ 点睛：本题的核心问题是计算数量积，求两个向量的数量积有三种方法：利用定义；利用向量的坐标运算；利用数量积的几何意义．具体应用时可根据已知条件的特征来选择，同时要注意数量积运算律的应用．‎ 例7．【2019届河南省南阳市第一中学高三第十四次考】若非零向量，满足，则在方向上的投影为__________．‎ ‎【答案】-1‎ ‎【解析】分析：先求出、和与的夹角，然后根据投影的定义求解．‎ 详解：将两边平方整理得，‎ ‎∴．‎ 将两边平方整理得．‎ 又，故．‎ 设向量与的夹角为，‎ 则在方向上的投影为 ‎．‎ 13‎ 点睛：解答本题的关键是正确掌握一个向量在另一个向量方向上的投影的定义，利用定义可将问题转化为数量积的运算．另外，数量积的几何意义是计算数量积的一种重要方法． ‎ 例8．已知点在椭圆上，点满足（）（是坐标原点），且，则线段在轴上的设影长度的最大值为__________．‎ ‎【答案】15‎ ‎【解析】∵，‎ 则线段OP在x轴上的投影长度为 ‎，当且仅当，即时等号成立．‎ ‎∴线段OP在x轴上的投影长度的最大值为15.‎ 答案：15‎ 例9.【2019届河北省衡水中学高三第十次模拟】若平面向量， 满足，则在方向上投影的最大值是________．‎ ‎【答案】‎ 13‎ ‎【解析】由可得： ‎ ‎∴‎ 在方向上投影为 故最大值为： ‎ 例10.【2019届河南省中原名校高三上第一次考评】已知P是边长为2的正△ABC边BC上的动点，则· （＋）＝_________．‎ ‎【答案】6‎ ‎【解析】设BC的中点为D，则AD⊥BC，‎ ‎【精选精练】‎ ‎1．【2019届山东省淄博市部分学校高三12月摸底】已知向量，则向量在向量上的投影是 A. 2 B. 1 C. -1 D. -2‎ 13‎ ‎【答案】D ‎【解析】向量在向量上的投影是 ,选D.‎ ‎2.【2019届河南省商丘市高三第二次模拟】已知平面向量，且，则在上的投影为（ ）‎ A. B. 2 C. D. 1‎ ‎【答案】A ‎【解析】因为，所以所以 所以所以在上的投影为 故选A.‎ ‎3．【2019届河北省武邑中学高三上学期期末】已知点，则向量在方向上的投影为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】， ，向量在方向上的投影为，故选A．‎ ‎4．【2019届贵州省遵义市高三上学期第二次联考】已知向量的夹角为60°，且，则向量在向量方向上的投影为（ ）‎ A. -1 B. 1 C. 2 D. 3‎ ‎【答案】B 13‎ ‎5．【2019届江西省南昌市高三第一轮复习训练】已知向量， 满足，且，则向量 在方向上的投影为(　　)‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由=（1，2），可得||=， •（+）=2，可得•+=2，‎ ‎∴=﹣3，∴向量在方向上的投影为.‎ 故答案为：D.‎ ‎6.已知的外接圆的圆心为，半径为2，且，则向量在向量方向上的投影为( )‎ A. 3 B. C. -3 D. ‎ ‎【答案】B ‎【解析】△ABC的外接圆的圆心为O,半径为2,且，‎ 13‎ 本题选择B选项.‎ ‎7．【2019届河南省郑州市第一中学高三上学期入学】的外接圆的圆心为，半径为1， ，且，则向量在向量方向上的投影为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】由题意可得： ，即： ,‎ 即外接圆的圆心为边的中点，则是以为斜边的直角三角形，‎ 结合有： ，‎ 则向量在向量方向上的投影为.‎ 本题选择D选项.‎ ‎8.【2019届湖南省（长郡中学、衡阳八中）、江西省（南昌二中）等十四校高三第二次联考】已知向量， 满足， ， ，则向量在向量上的投影为__________．‎ ‎【答案】‎ 13‎ ‎9．【2019届广西桂林、贺州、崇左三市高三第二次联合调研】已知向量， 的夹角为，且， ，则向量在向量方向上的投影为__________．‎ ‎【答案】‎ ‎【解析】投影为.‎ ‎10．【2019届衡水金卷一】已知向量，若向量与共线，则向量在向量放向上的投影为__________．‎ ‎【答案】0‎ ‎【解析】向量， ，向量，∵向量与共线，∴，即，∴向量，∴向量在向量方向上的投影为，故答案为0.‎ ‎11．已知向量，，若向量在方向上的投影为1，则__________．‎ ‎【答案】‎ ‎【解析】∵向量，,向量在方向上的投影长为1‎ ‎∴解得.‎ 13‎ 故答案为：.‎ ‎12．已知为直角三角形的外接圆，是斜边上的高，且，，点为线段的中点，若是中绕圆心运动的一条直径，则_________‎ ‎【答案】-5‎ ‎，所以解得，再由为的中点可得，所以，进而 ‎ 答案： .‎ 13‎