高考冲刺样本102圆锥曲线方程试题精粹3

高考冲刺样本102圆锥曲线方程试题精粹3

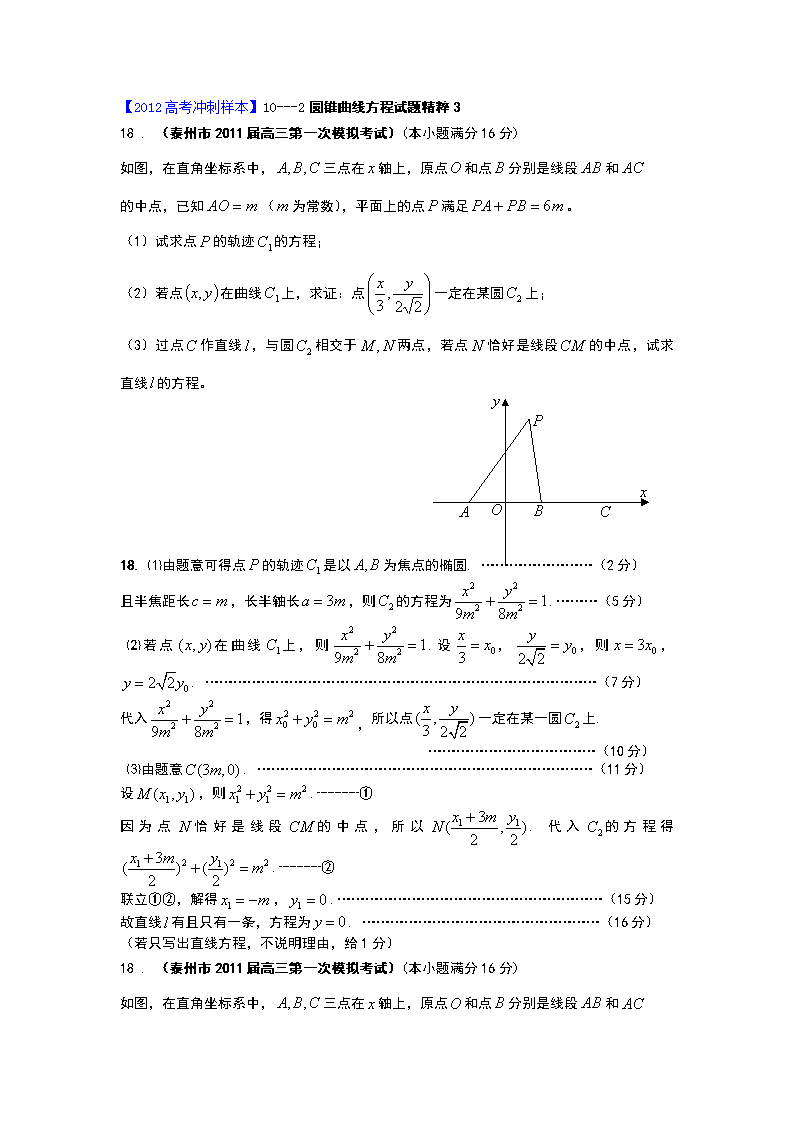
【2012高考冲刺样本】10---2圆锥曲线方程试题精粹3‎ ‎18 . （泰州市2011届高三第一次模拟考试）(本小题满分16分)‎ 如图，在直角坐标系中，三点在轴上，原点和点分别是线段和 的中点，已知（为常数），平面上的点满足。‎ ‎（1）试求点的轨迹的方程；‎ ‎（2）若点在曲线上，求证：点一定在某圆上；‎ ‎（3）过点作直线，与圆相交于两点，若点恰好是线段的中点，试求直线的方程。‎ ‎18. ⑴由题意可得点的轨迹是以为焦点的椭圆. ……………………（2分）‎ 且半焦距长，长半轴长，则的方程为.………（5分）‎ ‎⑵若点在曲线上，则.设，，则，. …………………………………………………………………………（7分）‎ 代入，得，所以点一定在某一圆上. ‎ ‎ ………………………………（10分）‎ ‎ ⑶由题意. ………………………………………………………………（11分）‎ 设，则.┈┈┈①‎ 因为点恰好是线段的中点，所以. 代入的方程得.┈┈┈②‎ 联立①②，解得，.…………………………………………………（15分）‎ 故直线有且只有一条，方程为. ……………………………………………（16分）‎ ‎（若只写出直线方程，不说明理由，给1分）‎ ‎18 . （泰州市2011届高三第一次模拟考试）(本小题满分16分)‎ 如图，在直角坐标系中，三点在轴上，原点和点分别是线段和 的中点，已知（为常数），平面上的点满足。‎ ‎（1）试求点的轨迹的方程；‎ ‎（2）若点在曲线上，求证：点一定在某圆上；‎ ‎（3）过点作直线，与圆相交于两点，若点恰好是线段的中点，试求直线的方程。‎ ‎18. ⑴由题意可得点的轨迹是以为焦点的椭圆. ……………………（2分）‎ 且半焦距长，长半轴长，则的方程为.………（5分）‎ ‎⑵若点在曲线上，则.设，，则，. …………………………………………………………………………（7分）‎ 代入，得，所以点一定在某一圆上. ‎ ‎ ………………………………（10分）‎ ‎ ⑶由题意. ………………………………………………………………（11分）‎ 设，则.┈┈┈①‎ 因为点恰好是线段的中点，所以. 代入的方程得.┈┈┈②‎ 联立①②，解得，.…………………………………………………（15分）‎ 故直线有且只有一条，方程为. ……………………………………………（16分）‎ ‎（若只写出直线方程，不说明理由，给1分）‎ ‎18．（江苏省南通市2011届高三第一次调研测试）（本题满分15分）‎ ‎（第18题）‎ 如图，已知椭圆的左、右顶点分别为A、B，右焦点为F，直线l为椭圆的右准线，N为l上一动点，且在x轴上方，直线AN与椭圆交于点M．‎ ‎（1）若AM=MN，求∠AMB的余弦值；‎ ‎（2）设过A，F，N三点的圆与y轴交于P，Q两点，当 线段PQ的中点坐标为（0，9）时，求这个圆的方程．‎ 解：（1）由已知，，直线．‎ 设N（8，t）（t>0），因为AM=MN，所以M（4，）．‎ 由M在椭圆上，得t=6．故所求的点M的坐标为M（4，3）．……………4分 所以，．‎ ‎．………………………7分 ‎（用余弦定理也可求得）‎ ‎（2）设圆的方程为，将A，F，N三点坐标代入，得 ‎∵ 圆方程为，令，得．…11分 设，则．‎ 由线段PQ的中点坐标为（0，9），得，．‎ 此时所求圆的方程为．………………………15分 ‎ ‎（本题用韦达定理也可解）‎ ‎（2）（法二）由圆过点A、F得圆心横坐标为－1，由圆与y轴交点的纵坐标为（0，9），‎ 得圆心的纵坐标为9，故圆心坐标为（－1，9）．…………………… 11分 易求得圆的半径为，………………………………………………13分 所以，所求圆的方程为．……………………… 15分 ‎18. （苏北四市2011届高三第一次调研考试）（本小题满分16分）‎ 已知椭圆E：的左焦点为F，左准线与x轴的交点是圆C的圆心，圆C恰好经过坐标原点O，设G是圆C上任意一点.‎ ‎（1）求圆C的方程；‎ ‎（2）若直线FG与直线交于点T，且G为线段FT的中点，求直线FG被圆C所截得的弦长；‎ ‎（3）在平面上是否存在定点P，使得？若存在，求出点P坐标；若不存在，请说明理由.‎ 讲评建议：对于第二问题当初是仿照2004年江苏高考题命制，用，考查两解情况，后改为，但综合全题还是有一线教师认为运算量较大，后改为现在情况，改成中点后，命题思想完全发生了变化，改成中点，学生用中点坐标公式，是代数方法，而原来思维是方程思想，这一点引起各位注意，对于第三问，也是教材的习题，逆向思维，同时是对两个参量求最值，学生一般接触较少，当然此题也可转化成一个参数，即对平方法，两次用圆方程消元，达到目的，建议教师讲解。同时注意到，此圆是以椭圆的左准线的与x轴的交点为圆心，两个定点恰是椭圆的左右焦点，三问题之间非常和谐，融为一体。‎ ‎18．（1）由椭圆E：，得：，，，‎ 又圆C过原点，所以圆C的方程为．………………………………4分 ‎（2）由题意，得，代入，得，‎ 所以的斜率为，的方程为， …………………8分 ‎（注意：若点G或FG方程只写一种情况扣1分）‎ 所以到的距离为，直线被圆C截得弦长为．‎ 故直线被圆C截得弦长为7．…………………………………………………………10分 ‎（3）设，，则由，得，‎ 整理得①，…………………………12分 又在圆C：上，所以②，‎ ‎②代入①得， …………………………14分 又由为圆C 上任意一点可知，解得．‎ 所以在平面上存在一点P，其坐标为． …………………………16分 ‎18、（宿迁市高三12月联考）（本题满分16分）已知椭圆的中心为坐标原点O，椭圆短轴长为2，动点 在椭圆的准线上。‎ ‎（1）求椭圆的标准方程；‎ ‎（2）求以OM为直径且被直线截得的弦长为2的圆的方程；‎ ‎（3）设F是椭圆的右焦点，过点F作OM的垂线与以OM为直径的圆交于点N，求证：线段ON的长为定值，并求出这个定值。‎ ‎18、解：（1）由，得 ……………1分 又由点M在准线上，得 ……………2分 故， 从而 ……………4分 所以椭圆方程为 ……………5分 ‎（2）以OM为直径的圆的方程为 即 ‎ 其圆心为,半径 ……………7分 因为以OM为直径的圆被直线截得的弦长为2‎ 所以圆心到直线的距离 ……………9分 所以，解得 所求圆的方程为 ……………10分 ‎（3）方法一：由平几知：‎ 直线OM：，直线FN： ……………12分 由得 所以线段ON的长为定值。 ……………16分 方法二、设，则 又 所以，为定值。‎ ‎18．（无锡市1月期末调研）(本小题满分16分) ‎ 已知椭圆 的左顶点为A，过A作两条互相垂直的弦AM、AN交椭圆于M、N两点．‎ （1） 当直线AM的斜率为时，求点M的坐标；‎ （2） 当直线AM的斜率变化时，直线MN是否过轴上的一定点，若过定点，请给出证明，并求出该定点，若不过定点，请说明理由．‎ ‎18．（1）直线AM的斜率为时，直线AM：， ………………………………1分 代入椭圆方程并化简得：， ……………………………2分 解之得，∴． ……………………………………4分 ‎（2）设直线AM的斜率为，则AM：，‎ 则　化简得：．……………6分 ‎∵此方程有一根为，∴， ……………………………………7分 同理可得．…………………………………………………………8分 由（1）知若存在定点，则此点必为．…………………………………9分 ‎∵，……………………………11分 同理可计算得．………………………………………………13分 ‎∴直线MN过轴上的一定点． ……………………………………16分 ‎19．（徐州市12月高三调研）(本小题满分16分)‎ P 第19题 x y A F1‎ F2‎ ‎·‎ M O 已知椭圆：的左、右焦点分别为，下顶点为，点是椭圆上任一点，⊙是以为直径的圆.‎ ‎（Ⅰ）当⊙的面积为时，求所在直线的方程；‎ ‎（Ⅱ）当⊙与直线相切时，求⊙的方程；‎ ‎（Ⅲ）求证：⊙总与某个定圆相切.‎ ‎·‎ ‎19．解：（Ⅰ）易得，设点P，‎ 则，所以…3分 又⊙的面积为，∴，解得，∴，‎ ‎∴所在直线方程为或………………5分 ‎（Ⅱ）因为直线的方程为，且到直线的 距离为………………………………7分 化简，得，联立方程组，解得或…10分 ‎∴当时，可得，∴⊙的方程为；‎ 当时，可得，∴⊙的方程为…12分 ‎（Ⅲ）⊙始终和以原点为圆心，半径为（长半轴）的圆（记作⊙）相切…13分 证明：因为，‎ 又⊙的半径，∴，∴⊙和⊙相内切…16分