2019届高考数学一轮复习 第八章 第5讲 椭圆1学案（无答案）文

2019届高考数学一轮复习 第八章 第5讲 椭圆1学案（无答案）文

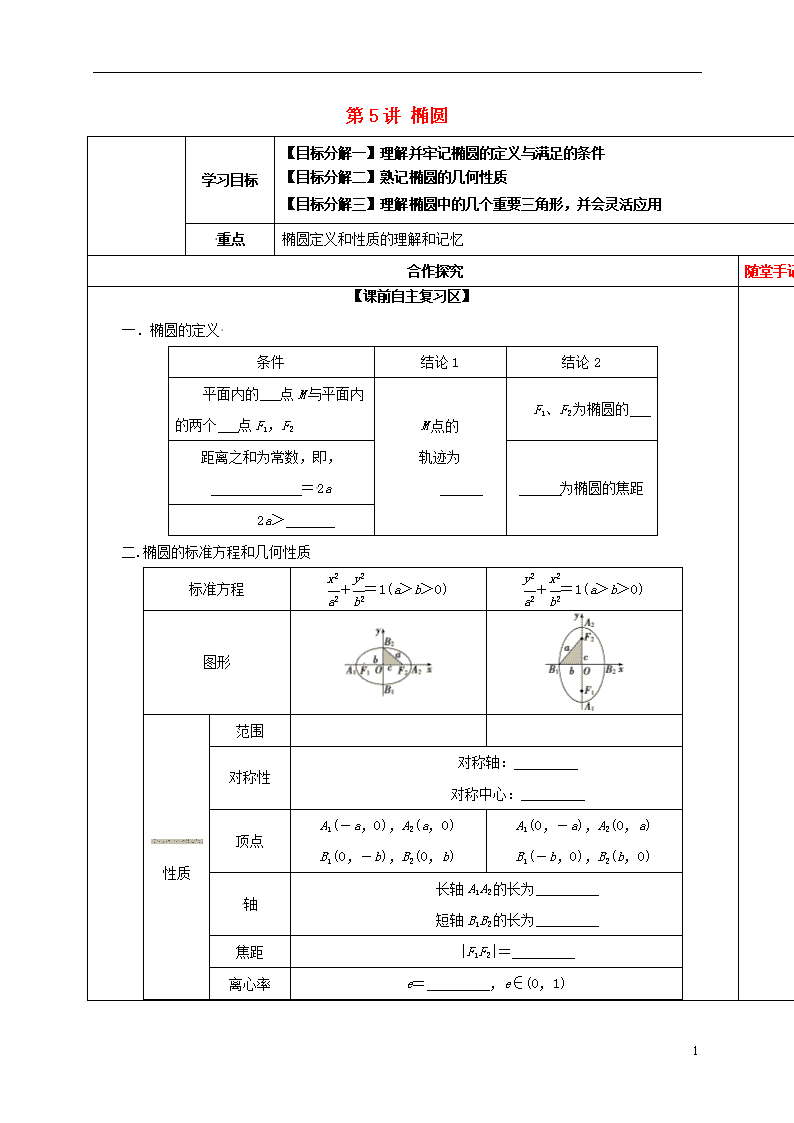
1 第 5 讲 椭圆 学习目标 【目标分解一】理解并牢记椭圆的定义与满足的条件 【目标分解二】熟记椭圆的几何性质 【目标分解三】理解椭圆中的几个重要三角形，并会灵活应用 重点 椭圆定义和性质的理解和记忆 合作探究 随堂手记 【课前自主复习区】 一．椭圆的定义 条件 结论 1 结论 2 平面内的 点 M 与平面内 的两个 点 F1，F2 F1、F2 为椭圆的 距离之和为常数，即， ＝2a 2a＞ M 点的 轨迹为 为椭圆的焦距 二.椭圆的标准方程和几何性质 标准方程 x2 a2＋y2 b2＝1(a＞b＞0) y2 a2＋x2 b2＝1(a＞b＞0) 图形 范围 对称性 对称轴： 对称中心： 顶点 A1(－a，0)，A2(a，0) B1(0，－b)，B2(0，b) A1(0，－a)，A2(0，a) B1(－b，0)，B2(b，0) 轴 长轴 A1A2 的长为 短轴 B1B2 的长为 焦距 |F1F2|＝ 性质 离心率 e＝ ，e∈(0，1) 2 a，b，c 的关系 a2＝ 三、要点整合 1.椭圆的定义中 2a＞|F1F2|条件不可缺，当 2a＝|F1F2| 时，其轨迹为 ，当 2a＜|F1F2|时， ． 2.求椭圆的标准方程时易忽视判断焦点的位置。焦点位 置的判断依据为： 。 3.椭圆中几个比较重要的三角形： ①特征三角形【如 右图：含有 a，b，c 关系】 ②焦点三角形【椭圆上一点 A 与椭圆的两焦点 F1，F2 组成的三角形通常称为 “焦点三角形”，利用定义可求其周长；利用定义和余弦定理可求 |AF1||AF2|；通过整体代入可求其面积等．】 ③以焦点弦为一条底边，另一焦点为顶点的三角形（请补充画完示意图） 【结论：1°周长为定值 2°面积的简单求法： 】 四、课前自测区 1.教材习题改编 椭圆 C：x2 25＋y2 16＝1 的左右焦点分别为 F1，F2，过 F2 的直线交椭圆 C 于 A、B 两点， 则△F1AB的周长为(　　) A．12　　　　　　　　 B．16 C．20 D．24 2．若直线 x－2y＋2＝0 经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为(　　) A.x2 5 ＋y2＝1 B．x2 4 ＋y2 5 ＝1 C.x2 5 ＋y2＝1 或x2 4 ＋y2 5 ＝1 D．以上答案都不对 3．(2016·高考全国卷乙)直线 l 经过椭圆的一个顶点和一个焦点，若椭圆中心到 l 的距离为其短轴 长的1 4，则该椭圆的离心率为(　　) 3 A.1 3　　 B．1 2 C.2 3 D．3 4 4．若方程 x2 5－k＋ y2 k－3＝1 表示椭圆，则 k 的取值范围是________． 5．已知椭圆的中心在原点，焦 点在 x 轴上，离心 率为 5 5 ，且过点 P(－5，4)，则椭圆的标准方程 为________．