全国高考文科数学立体几何综合题型汇总

全国高考文科数学立体几何综合题型汇总

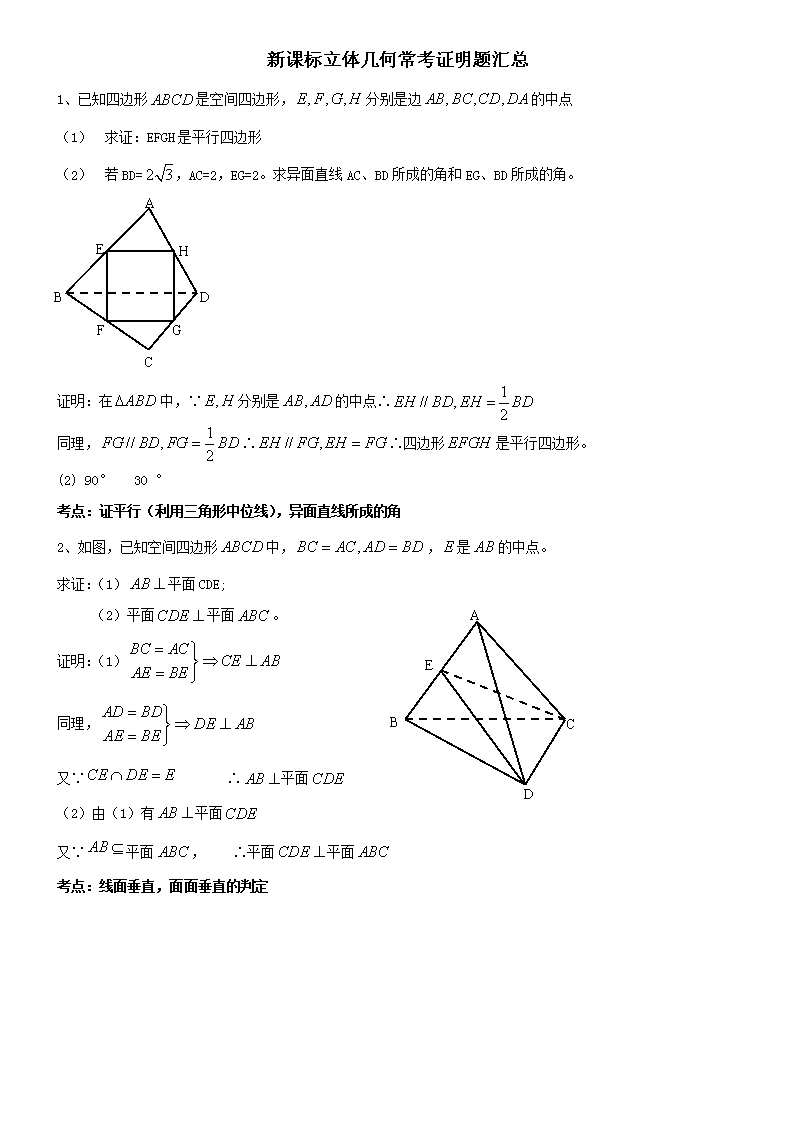
新课标立体几何常考证明题汇总 ‎1、已知四边形是空间四边形，分别是边的中点 （1） 求证：EFGH是平行四边形 A H G F E D C B （2） 若BD=，AC=2，EG=2。求异面直线AC、BD所成的角和EG、BD所成的角。‎ 证明：在中，∵分别是的中点∴‎ 同理，∴∴四边形是平行四边形。‎ ‎(2) 90° 30 °‎ 考点：证平行（利用三角形中位线），异面直线所成的角 ‎2、如图，已知空间四边形中，，是的中点。‎ 求证：（1）平面CDE;‎ A E D B C ‎（2）平面平面。 ‎ 证明：（1）‎ 同理，‎ 又∵ ∴平面 ‎（2）由（1）有平面 又∵平面， ∴平面平面 考点：线面垂直，面面垂直的判定 A1‎ E D1‎ C1‎ B1‎ D C B A ‎3、如图，在正方体中，是的中点，‎ 求证： 平面。‎ 证明：连接交于，连接，‎ ‎∵为的中点，为的中点 ‎∴为三角形的中位线 ∴‎ 又在平面内，在平面外 ‎∴平面。 ‎ 考点：线面平行的判定 ‎4、已知中,面,,求证：面．‎ 证明：° ‎ ‎ 又面 ‎ ‎ 面 ‎ ‎ ‎ 又面 ‎ 考点：线面垂直的判定 ‎5、已知正方体，是底对角线的交点.‎ 求证：(１) C1O∥面；(2)面． ‎ 证明：（1）连结，设，连结 ‎∵ 是正方体 是平行四边形 ‎∴A1C1∥AC且 ‎ 又分别是的中点，∴O1C1∥AO且 是平行四边形 ‎ 面，面 ∴C1O∥面 ‎ ‎（2）面 ‎ 又， ‎ 同理可证， 又 面 ‎ 考点：线面平行的判定（利用平行四边形），线面垂直的判定 ‎6、正方体中，求证：（1）；（2）.‎ 考点：线面垂直的判定 A1‎ A B1‎ B C1‎ C D1‎ D G E F ‎7、正方体ABCD—A1B‎1C1D1中．(1)求证：平面A1BD∥平面B1D‎1C；‎ ‎ (2)若E、F分别是AA1，CC1的中点，求证：平面EB1D1∥平面FBD．‎ 证明：(1)由B1B∥DD1，得四边形BB1D1D是平行四边形，∴B1D1∥BD，‎ ‎ 又BD Ë平面B1D‎1C，B1D1平面B1D‎1C，‎ ‎ ∴BD∥平面B1D‎1C．‎ ‎ 同理A1D∥平面B1D‎1C．‎ ‎ 而A1D∩BD＝D，∴平面A1BD∥平面B1CD．‎ ‎ (2)由BD∥B1D1，得BD∥平面EB1D1．取BB1中点G，∴AE∥B‎1G．‎ ‎ 从而得B1E∥AG，同理GF∥AD．∴AG∥DF．∴B1E∥DF．∴DF∥平面EB1D1．∴平面EB1D1∥平面FBD．‎ 考点：线面平行的判定（利用平行四边形）‎ ‎8、四面体中，分别为的中点，且，‎ ‎，求证：平面 ‎ 证明：取的中点，连结，∵分别为的中点，∴‎ ‎，又∴，∴在中，‎ ‎ ∴，∴，又，即，‎ ‎ ∴平面 ‎ 考点：线面垂直的判定,三角形中位线，构造直角三角形 ‎9、如图是所在平面外一点，平面，是的中点，是上的点，‎ ‎（1）求证：；（2）当，时，求的长。‎ 证明：（1）取的中点，连结，∵是的中点，‎ ‎∴，∵ 平面 ，∴ 平面 ‎ ‎∴是在平面内的射影 ，取 的中点，连结 ，∵∴，又，∴[来源:学§科§网]‎ ‎ ∴，∴，由三垂线定理得 ‎ （2）∵，∴，∴，∵平面.∴，且 ‎，∴‎ 考点：三垂线定理 ‎10、如图，在正方体中，、、分别是、、的中点.求证：平面∥平面.‎ 证明：∵、分别是、的中点，∥‎ 又平面，平面∥平面 ‎∵四边形为平行四边形，∥‎ 又平面，平面∥平面 ‎，平面∥平面 考点：线面平行的判定（利用三角形中位线）‎ ‎11、如图，在正方体中，是的中点.‎ ‎（1）求证：平面；‎ ‎（2）求证：平面平面.‎ 证明：（1）设，‎ ‎∵、分别是、的中点，∥‎ 又平面，平面，∥平面 ‎（2）∵平面，平面，‎ 又，，平面，平面，平面平面 考点：线面平行的判定（利用三角形中位线），面面垂直的判定 ‎12、已知是矩形，平面，，，为的中点．‎ ‎（1）求证：平面；（2）求直线与平面所成的角．‎ 证明：在中，，‎ ‎∵平面，平面，‎ 又，平面 ‎（2）为与平面所成的角 在，，在中，‎ 在中，，‎ 考点：线面垂直的判定,构造直角三角形 ‎13、如图，在四棱锥中，底面是且边长为的菱形，侧面是等边三角形，且平面垂直于底面．‎ ‎（1）若为的中点，求证：平面；‎ ‎（2）求证：；‎ ‎（3）求二面角的大小．‎ 证明：（1）为等边三角形且为的中点，‎ 又平面平面，平面 ‎（2）是等边三角形且为的中点，‎ 且，，平面，‎ 平面，‎ ‎（3）由，∥，‎ 又，∥，‎ 为二面角的平面角 在中，，‎ 考点：线面垂直的判定,构造直角三角形,面面垂直的性质定理，二面角的求法（定义法）‎ ‎14、如图1,在正方体中，为 的中点，AC交BD于点O，求证：平面MBD．‎ 证明：连结MO，，∵DB⊥，DB⊥AC，， ‎ ‎∴DB⊥平面，而平面 ∴DB⊥． ‎ 设正方体棱长为，则，．‎ 在Rt△中，．∵，∴． ‎ ‎∵OM∩DB=O，∴ ⊥平面MBD．‎ 考点：线面垂直的判定，运用勾股定理寻求线线垂直 ‎15、如图２，在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，‎ 作BE⊥CD，Ｅ为垂足，作AH⊥BE于Ｈ．求证：AH⊥平面BCD．‎ ‎ 证明：取AB的中点Ｆ，连结CF，DF．‎ ‎ ∵，∴． ‎ ‎ ∵，∴．‎ ‎ 又，∴平面CDF．‎ ‎ ∵平面CDF，∴．‎ ‎ 又，，　‎ ‎ ∴平面ABE，．‎ ‎ ∵，，，‎ ‎∴ 平面BCD．‎ 考点：线面垂直的判定