江苏高考数学卷分析总体分析

江苏高考数学卷分析总体分析

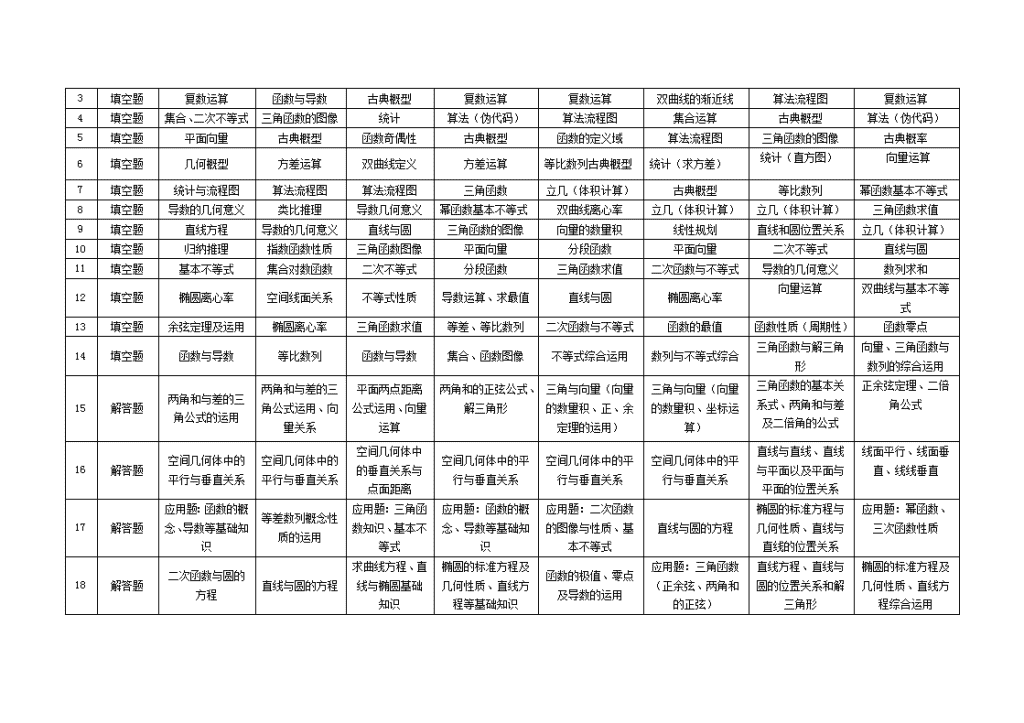
‎2015年高考数学（江苏卷）试题分析 一、考试形式及试卷结构 ‎（一）考试形式 闭卷、笔试，试题分必做题和附加题两部分。必做题部分满分为160分，考试时间120分钟；附加题部分满分为40分，考试时间30分钟。‎ ‎（二）考试题型 ‎1．必做题 必做题部分由填空题和解答题两种题型组成。其中填空题14小题，约占70分；解答题6小题，约占90分。‎ ‎2．附加题 附加题部分由解答题组成，共6题.其中，必做题2小题，考查选修系列2（不含选修系列1）中的内容；选做题共4小题，依次考查选修系列4中4-1、4-2、4-4、4-5这4个专题的内容，考生只须从中选2个小题作答。‎ 填空题着重考查基础知识、基本技能和基本方法，只要求直接写出结果，不必写出计算和推理过程；解答题应写出文字说明、证明过程或演算步骤。‎ ‎（三）试题难易比例 必做题部分由容易题、中等题和难题形式组成。容易题、中等题和难题在试卷中的比例大致为4：4：2。‎ 附加题部分由容易题、中等题和难题形式组成。容易题、中等题和难题在试卷中的比例大致为5：4：1。‎ 二、试卷概述 一卷部分（即文理同卷部分），总体上说，试题的难易程度适中。‎ 填空题（1-14题），与过去7年（08年-14年）相比，前12题相对较容易，第13题与去年的第13题考查的一样，即函数与方程的零点问题，难度高于去年，且易错；第14题较难。分析如下：‎ ‎1-9题，比较容易。并且前五道题是最容易拿分且每年必考的集合、统计、复数、算法与概率。这45分应该是很多考生可以轻而易举拿到的分数。‎ ‎10-12题，难度适中。第10题与2012年的第13题相类似，且更加容易，直接考查直线与圆相切，之后用函数思想和基本不等式解决问题；第11题，考查累加法求通项及裂相相消求和；作为数列填空题出在第11题的位置，而且又比较简单，也应该是可以拿分的题目；第12题，考查双曲线的渐近线与平行直线之间的距离问题，知识点较简单，考法比较新颖，与往年这个位置的解析几何相比，难度不大，且运算量较小。‎ ‎13、14题，难度较大。第13题，考查分段函数、函数与方程的零点问题，且带有绝对值。解题步骤非常简单，首先去掉绝对值，当成两组函数的交点问题，再分别画出函数图像，答案便一目了然。第14题，考查了向量、三角函数与数列的综合运用，难度较大。‎ 解答题（15-20题），前两题（15-16题）纯属送分题，比过去6年（08年-13年）的任何一题都要容易的多，与14年难度接近，很多考生都可以轻松解答。分析如下：‎ 第15题，与去年14年难度类似，相比之前（08年-13年）任何一题，都简单许多，几乎没有任何技巧而言，直接运用正余弦定理即可。只要步骤写详细这14分是比较容易拿到的。‎ 第16题，可以说是历年来最简单的。同样需要步骤写详细，防止因此失分。‎ 第17题，可以说是近年来最简单的一道应用题，第二问用导数写出切线方程，再用导数求出最值。‎ 第18题解析几何，同时考查了中点弦与焦点弦的问题，当然最后的运算量较大，但从点差法与第二定义入手，应该很快就能够把关系式找到。‎ 第19题，函数导数问题，第一问比较简单，简单的分类讨论即可；第二问较新颖，但很容易入手，仍然遵循求导的几个步骤，之后再对a进行分类讨论。‎ 第20题，数列，符合近些年江苏卷对于数列部分出题的思路，属非常规题型。第一问较简单，送4分；第二问与第三问，非常难，运算量较大，技巧性也较强，完全符合一卷最后一题的特点。‎ 二卷部分（理科考生的附加题部分）‎ 前两题，即前20分。大多数考生都选择的是矩阵和极坐标，属于必拿的分数。‎ 第三题，命题内容似乎有些规律。2011年和2013年考空间向量；2012年与2014考数学期望；今年再次是空间向量。‎ 第四题，与过去11-13年类似，再次回到排列组合，属于拉开区分度的压轴题。第一问只需耐心列举，仍然可以拿到4分，第二问尽量多写，并且这次还考到了数学归纳法，相对来说更容易些。‎ ‎ 年份 ‎ 考查的 ‎ 知识点 题号 题型 ‎2008年 ‎2009年 ‎2010年 ‎2011年 ‎2012年 ‎2013年 ‎2014年 ‎2015年 ‎1‎ 填空题 三角函数的周期 复数运算 集合运算 集合运算 集合运算 三角函数的周期 集合的概念 集合 ‎2‎ 填空题 古典概型 平面向量 复数运算 函数单调性 统计(分层抽样）‎ 复数运算 复数运算 平均数运算 ‎3‎ 填空题 复数运算 函数与导数 古典概型 复数运算 复数运算 双曲线的渐近线 算法流程图 复数运算 ‎4‎ 填空题 集合、二次不等式 三角函数的图像 统计 算法（伪代码）‎ 算法流程图 集合运算 古典概型 算法（伪代码）‎ ‎5‎ 填空题 平面向量 古典概型 函数奇偶性 古典概型 函数的定义域 算法流程图 三角函数的图像 古典概率 ‎6‎ 填空题 几何概型 方差运算 双曲线定义 方差运算 等比数列古典概型 统计（求方差）‎ 统计（直方图）‎ 向量运算 ‎7‎ 填空题 统计与流程图 算法流程图 算法流程图 三角函数 立几（体积计算）‎ 古典概型 等比数列 幂函数基本不等式 ‎8‎ 填空题 导数的几何意义 类比推理 导数几何意义 幂函数基本不等式 双曲线离心率 立几（体积计算）‎ 立几（体积计算）‎ 三角函数求值 ‎9‎ 填空题 直线方程 导数的几何意义 直线与圆 三角函数的图像 向量的数量积 线性规划 直线和圆位置关系 立几（体积计算）‎ ‎10‎ 填空题 归纳推理 指数函数性质 三角函数图像 平面向量 分段函数 平面向量 二次不等式 直线与圆 ‎11‎ 填空题 基本不等式 集合对数函数 二次不等式 分段函数 三角函数求值 二次函数与不等式 导数的几何意义 数列求和 ‎12‎ 填空题 椭圆离心率 空间线面关系 不等式性质 导数运算、求最值 直线与圆 椭圆离心率 向量运算 双曲线与基本不等式 ‎13‎ 填空题 余弦定理及运用 椭圆离心率 三角函数求值 等差、等比数列 二次函数与不等式 函数的最值 函数性质（周期性）‎ 函数零点 ‎14‎ 填空题 函数与导数 等比数列 函数与导数 集合、函数图像 不等式综合运用 数列与不等式综合 三角函数与解三角形 向量、三角函数与数列的综合运用 ‎15‎ 解答题 两角和与差的三角公式的运用 两角和与差的三角公式运用、向量关系 平面两点距离公式运用、向量运算 两角和的正弦公式、解三角形 三角与向量（向量的数量积、正、余定理的运用）‎ 三角与向量（向量的数量积、坐标运算）‎ 三角函数的基本关系式、两角和与差及二倍角的公式 正余弦定理、二倍角公式 ‎16‎ 解答题 空间几何体中的平行与垂直关系 空间几何体中的平行与垂直关系 空间几何体中的垂直关系与点面距离 空间几何体中的平行与垂直关系 空间几何体中的平行与垂直关系 空间几何体中的平行与垂直关系 直线与直线、直线与平面以及平面与平面的位置关系 线面平行、线面垂直、线线垂直 ‎17‎ 解答题 应用题：函数的概念、导数等基础知识 等差数列概念性质的运用 应用题：三角函数知识、基本不等式 应用题：函数的概念、导数等基础知识 应用题：二次函数的图像与性质、基本不等式 直线与圆的方程 椭圆的标准方程与几何性质、直线与直线的位置关系 应用题：幂函数、三次函数性质 ‎18‎ 解答题 二次函数与圆的方程 直线与圆的方程 求曲线方程、直线与椭圆基础知识 椭圆的标准方程及几何性质、直线方程等基础知识 函数的极值、零点及导数的运用 应用题：三角函数（正余弦、两角和的正弦）‎ 直线方程、直线与圆的位置关系和解三角形 椭圆的标准方程及几何性质、直线方程综合运用 ‎19‎ 解答题 等差、等比数列的综合运用 应用题：函数与不等式综合运用 数列与不等式的综合运用 函数的概念、性质及导数综合运用 椭圆的标准方程及几何性质、直线方程综合运用 等差、等比数列综合运用（推理证明）‎ 初等函数的基本性质、导数的应用 函数的概念、性质及导数综合运用 ‎20‎ 解答题 函数知识综合运用 一元二次不等式综合运用 函数的概念、性质及导数综合运用 等差数列基本性质的综合运用 等差、等比数列的定义、性质的综合运用 导数的运算及利用导数研究函数的性质 数列的概念、等差数列 等比数列的定义、性质的综合运用 ‎1、新题难题总结 ‎ 1～9题是体现最低要求的容易题，只需稍作运算即可顺利完成；10～14题复杂程度、能力要求和解题难度有所提升，对把握概念本质属性和运用数学思想方法提出较高要求，对考生的想像力、抽象度、灵活性、深刻性等思维品质提出更大的挑战。解答题着重考查综合运用知识，分析和解决数学问题的能力。‎ 第16题、第15与17题、第19题、第18与20题分别形成四个不同的水平层次。第一层次是基础知识和推理论证的最低要求；第二层次重在对知识和方法的综合运用，重在基本运算能力的要求；第三层次突出对知识和方法的灵活运用，加大了分析和解决问题的思考力度；第四层次重点是考查解决新问题的能力，体现了对考生的高层次数学思维能力的要求和高水平数学素质的要求。但是每道题设置由易到难2-3小问，对考生了提供启发性帮助。‎ ‎2、今年数学试卷最大的亮点 ‎　　 今年考题的最大亮点应该在于对重点模块的考察上，更侧重于对重点模块的考察。大多数的题，基本上都是可以按部就班的，按照我们平时的这些做题的步骤写出来了，而且侧重于学生的基础知识的考察，而且侧重于对学生能力的考察，比如说抽象概括能力，空间想象能力，推理论证能力，还有一些比如分析问题能力，解决问题的能力，侧重于这些能力的考察。‎ ‎3、与近几年高考试卷对比 ‎ 1、在最近两年的高考题提型基础上拓展变化。‎ ‎ 2、卷Ⅰ的填空题着重考查基础知识和基本技能，对数学能力考查体现不同的要求.‎ ‎ 3、高考数学科(江苏卷)考试对知识的考查要求依次分为了解(A)、理解(B)、掌握(C)三个层次。必做题部分A级考点29个，B级考点36个，C级考点8个。‎ 一级考点 二级考点 三级考点 分值 占试卷百比例 代数 集合 并集 ‎5‎ ‎2.50%‎ ‎ ‎ 基本初等函数 对数函数的定义域 ‎5‎ ‎2.50%‎ ‎ ‎ 函数的应用 函数模型的选择与应用 ‎14‎ ‎7.00%‎ ‎ ‎ 导数及其应用 函数性质 ‎16‎ ‎8.00%‎ ‎ ‎ 不等式 不等式求解集 ‎5‎ ‎2.50%‎ ‎ ‎ 数列 数列递推式 ‎ ‎5‎ ‎2.50%‎ ‎ ‎ ‎ ‎ 等比数列的性质 ‎16‎ ‎8.00%‎ ‎ ‎ 平面向量 向量运算 ‎5‎ ‎2.50%‎ ‎ ‎ 数系的扩充与复数 复数运算 ‎5‎ ‎2.50%‎ 排列组合与概率统计 统计与统计案例 平均数、概率 ‎10‎ ‎5.00%‎ 算法与框图 算法初步与框图 伪代码 ‎5‎ ‎2.50%‎ 三角函数 三角函数中的恒等变换应用 三角函数中的恒等变换应用 ‎5‎ ‎2.50%‎ ‎ ‎ 三角函数 解三角形 ‎14‎ ‎7.00%‎ 平面解析几何 圆与方程 直线与圆的位置关系 ‎5‎ ‎2.50%‎ 圆锥曲线与方程 直线与圆锥曲线的综合问题 ‎16‎ ‎8.00%‎ 直线与圆锥曲线的关系 ‎5‎ ‎2.50%‎ 立体几何 空间几何体 圆柱、圆锥的体积 ‎5‎ ‎2.50%‎ ‎ ‎ ‎ ‎ 线面平行的判定 ‎14‎ ‎7.00%‎