高考数学《坐标系与参数方程》专项练习(含答案)

高考数学《坐标系与参数方程》专项练习(含答案)

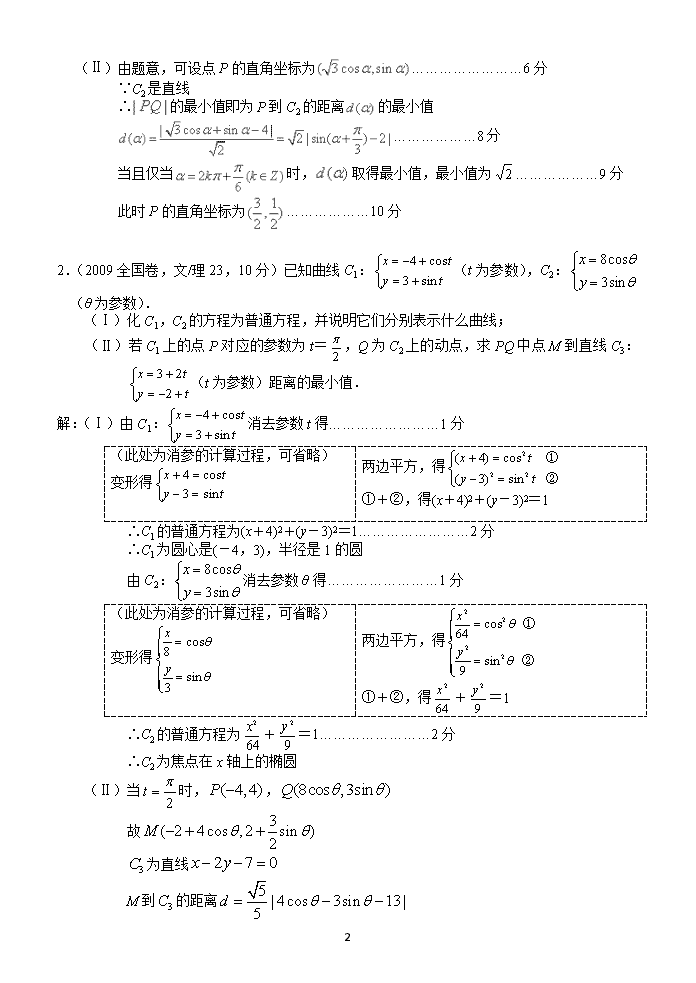
‎《坐标系与参数方程》专项练习 一、知识梳理．‎ ‎1．极坐标与直角坐标的互化．‎ 设M是平面内任意一点，它的直角坐标是(x，y)，极坐标是(ρ，θ)，则它们之间的关系为：‎ ‎（1），　　（2）‎ ‎2．参数方程(t为参数)化为普通方程的常用方法．‎ ‎（1）代入法/加减法消参．‎ ‎（2）借助三角恒等式sin2θ＋cos2θ＝1（θ为参数）消参．‎ ‎3．直角坐标方程，极坐标方程和参数方程的转化关系．‎ 极坐标方程 ‎(ρ，θ)‎ ‎⇔‎ 直角坐标方程(普通方程)‎ ‎(x，y)‎ ‎⇔‎ 参数方程 ‎(t为参数)‎ 二、练习专项．‎ ‎【题型1】①极坐标方程　⇔　直角坐标方程．‎ ‎②参数方程　⇔　直角坐标方程．‎ ‎1．（2016全国Ⅲ卷，文科23，10分）在直线坐标系xOy中，曲线C1的参数方程为 （α为参数）．以坐标原点为极点，x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为ρsin(θ＋)＝2．‎ ‎（Ⅰ）写出C1的普通方程和C2的直角坐标方程；‎ ‎（Ⅱ）设点P在C1上，点Q在C2上，求∣PQ∣的最小值及此时P的直角坐标．‎ 解：（Ⅰ）由消去参数α得……………………1分 ‎（此处为消参的计算过程，可省略）‎ 变形得 两边平方，得 ‎①＋②，得＋y2＝1‎ C1的普通方程为＋y2＝1……………………2分 ‎∵ρsin(θ＋)＝2‎ ‎∴ρ(sinθcos＋cosθsin)＝2……………………3分 ρ(sinθ＋cosθ)＝2‎ ρsinθ＋ρcosθ＝2‎ ρsinθ＋ρcosθ＝4……………………4分 ‎∵ρcosθ＝x，ρsinθ＝y ‎∴x＋y＝4……………………5分 9‎ ‎（Ⅱ）由题意，可设点P的直角坐标为……………………6分 ‎∵C2是直线 ‎∴的最小值即为P到C2的距离的最小值 ‎………………8分 当且仅当时，取得最小值，最小值为………………9分 此时P的直角坐标为………………10分 ‎2．（2009全国卷，文/理23，10分）已知曲线C1：（t为参数），C2：（θ为参数）．‎ ‎（Ⅰ）化C1，C2的方程为普通方程，并说明它们分别表示什么曲线；‎ ‎（Ⅱ）若C1上的点P对应的参数为t＝，Q为C2上的动点，求PQ中点M到直线C3：（t为参数）距离的最小值．‎ 解：（Ⅰ）由C1：消去参数t得……………………1分 ‎（此处为消参的计算过程，可省略）‎ 变形得 两边平方，得 ‎①＋②，得(x＋4)2＋(y－3)2＝1‎ ‎∴C1的普通方程为(x＋4)2＋(y－3)2＝1……………………2分 ‎∴C1为圆心是(－4，3)，半径是1的圆 由C2：消去参数θ得……………………1分 ‎（此处为消参的计算过程，可省略）‎ 变形得 两边平方，得 ‎①＋②，得＋＝1‎ ‎∴C2的普通方程为＋＝1……………………2分 ‎∴C2为焦点在x轴上的椭圆 ‎（Ⅱ）当时，，‎ 故 为直线 M到的距离 9‎ 从而当时，取得最小值 ‎【题型2】①直角坐标方程　⇔　极坐标方程．‎ ‎②直角坐标方程　⇔　参数方程．‎ ‎3．（2016全国Ⅱ卷，文科23，10分）在直角坐标系xOy中，圆C的方程为(x＋6)2＋y2＝25．‎ ‎（Ⅰ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求C的极坐标方程；‎ ‎（Ⅱ）直线l的参数方程是(t为参数)，l与C交于A，B两点，|AB|＝．‎ 求l的斜率．‎ 解：（Ⅰ）由圆C的方程可得……………………1分 x2＋12x＋36＋y2＝25‎ x2＋y2＋12x＋11＝0……………………2分 把x2＋y2＝ρ2，x＝ρcosθ代入上式得……………………3分 ρ2＋12ρcosθ＋11＝0……………………4分 ‎∴圆C的极坐标方程为ρ2＋12cosθ＋11＝0……………………5分 ‎（Ⅱ）在（Ⅰ）中建立的极坐标系中，直线l的极坐标方程为θ＝α(ρ∈R)‎ 由A，B所对应的极径分别为ρ1，ρ2……………………8分 将l的极坐标方程代入C的极坐标方程得 ρ2＋12ρcosα＋11＝0……………………7分 于是 ‎……………………8分 由|AB|＝得 ‎……………………9分 ‎∴l的斜率为或……………………10分 ‎4．（2015全国Ⅰ卷，文/理23，10分）在直角坐标系xOy中，直线C1：x＝－2，圆C2：(x－1)2＋(y－2)2＝1，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系．‎ ‎（Ⅰ）求C1，C2的极坐标方程；‎ ‎（Ⅱ）若直线C3的极坐标方程为θ＝(ρ∈R)，设C2与C3的交点为M，N，求△C2MN的面积．‎ 解：（Ⅰ）把x＝ρcosθ代入C1：x＝－2得ρcosθ＝－2……………………1分 ‎∴C1的极坐标方程为ρcosθ＝－2………………2分 由C2：(x－1)2＋(y－2)2＝1得 ‎(x2－2x＋1)＋(y2－4y＋4)＝1‎ x2＋y2－2x－4y＋1＋4＝1‎ x2＋y2－2x－4y＋4＝0………………3分 把ρ2＝x2＋y2，x＝ρcosθ，y＝ρsinθ代入上式得………………4分 C2的极坐标方程为ρ2－2ρcosθ－4ρsinθ＋4＝0………………5分 ‎（Ⅱ）将θ＝π‎4‎代入ρ2－2ρcosθ－4ρsinθ＋4＝0，得 ρ2－3‎2‎ρ＋4＝0………………6分 解得ρ1＝2‎2‎，ρ2＝‎2‎………………7分 故ρ1－ρ2＝‎2‎，即|MN|＝‎2‎………………8分 9‎ 由于C2的半径为1‎ ‎∴△C2MN的面积为‎1‎‎2‎………………10分 ‎5．（2014全国Ⅰ卷，文/理23，10分）已知曲线C：，直线l：(t为参数)．‎ ‎（Ⅰ）写出曲线C的参数方程，直线l的普通方程；‎ ‎（Ⅱ）过曲线C上任意一点P作与l夹角为30°的直线，交l于点A，求|PA|的最大值与最小值．‎ 解：（Ⅰ）∵曲线C：x‎2‎‎4‎‎＋‎y‎2‎‎9‎＝1‎ ‎∴‎ 又∵sin2θ＋cos2θ＝1‎ ‎∴＝cosθ，＝sinθ ‎∴x＝2cosθ，y＝3sinθ 曲线C的参数方程为(θ为参数)．‎ 由直线l：x＝2＋ty＝2－2t消去参数t得 ‎（此处为消参的计算过程，可省略）‎ x＝2＋t①　‎y＝2－2t②‎ 由①得t＝x－2　③‎ 把③代入②，得 y＝2－2(x－2)‎ 整理得2x＋y－6＝0‎ 直线l的普通方程为2x＋y－6＝0．‎ ‎（Ⅱ）曲线C上任意一点P(2cosθ，3sinθ)到l的距离为 d＝‎5‎‎5‎|4cosθ＋3sinθ－6|‎ 则|PA|＝dsin30°‎‎＝‎‎2‎‎5‎‎5‎|5sin(θ＋α)－6|，其中α为锐角，且tanα＝‎‎4‎‎3‎ 当sin(θ＋α)＝－1时，|PA|取得最大值，最大值为‎22‎‎5‎‎5‎ 当sin(θ＋α)＝1时，|PA|取得最小值，最小值为‎2‎‎5‎‎5‎ ‎6．（2014全国Ⅱ卷，文/理23，10分）在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，半圆C的极坐标方程为ρ＝2cosθ，θ∈[0，]．‎ ‎（Ⅰ）求C的参数方程；‎ ‎（Ⅱ）设点D在C上，C在D处的切线与直线l：y＝x＋2垂直，根据（Ⅰ）中你得到的参数方程，确定D的坐标．‎ 解：（Ⅰ）∵ρ＝2cosθ ‎∴ρ2＝2ρcosθ 把x2＋y2＝ρ2，x＝ρcosθ代入上式得 x2＋y2＝2x ‎∴C的普通方程为(x－1)2＋y2＝1(0≤y≤1)‎ ‎∴半圆C的圆心为(1，0)，半径为1‎ 9‎ 可得C的参数方程为x＝1＋costy＝sint(t为参数，0≤t≤π)‎ ‎（Ⅱ）设D(1＋cost，sint)‎ 由(Ⅰ)知C是以G(1，0)为圆心，1为半径的上半圆 ‎∵C在点D处的切线与l垂直 ‎∴直线GD与l的斜率相同．tant＝‎3‎，t＝‎π‎3‎ 故D的直角坐标为‎1＋cosπ‎3‎，sinπ‎3‎，即‎3‎‎2‎‎，‎‎3‎‎2‎ ‎【题型3】极坐标方程　⇔　参数方程．‎ ‎7．（2016全国Ⅰ卷，文/理23，10分）在直角坐标系xOy中，曲线C1的参数方程为（t为参数，a＞0）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝4cosθ．‎ ‎（Ⅰ）说明C1是哪一种曲线，并将C1的方程化为极坐标方程；‎ ‎（Ⅱ）直线C3的极坐标方程为θ＝α0，其中α0满足tanα0＝2，若曲线C1与C2的公共点都在C3上，求a．‎ 解：（Ⅰ）解法一：C1是圆的方程…………1分 由消去参数t得…………2分 ‎（此处为消参的计算过程，可省略）‎ 移项，得 两边平方，得 即 ‎①＋②，得 x2＋(y－1)2＝a2cos2t＋a2sin2t x2＋(y－1)2＝a2(cos2t＋sin2t)‎ x2＋(y－1)2＝a2‎ ‎　①‎ 整理得…………3分 ‎∴把代入上式得…………4分 ‎∴的极坐标方程为…………5分 ‎（Ⅱ）由C2：ρ＝4cosθ得 两边同乘ρ得ρ2＝4ρcosθ ‎∵ρ2＝x2＋y2，ρcosθ＝x ‎…………6分 即　②…………7分 C3：化为普通方程为…………8分 由题意：和的公共方程所在直线即为 ‎①－②得：，即为…………9分 ‎∴‎ ‎∴…………10分 9‎ ‎8．（2013全国Ⅰ卷，文/理23，10分）已知曲线C1的参数方程为(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sinθ．‎ ‎（Ⅰ）把C1的参数方程化为极坐标方程；‎ ‎（Ⅱ）求C1与C2交点的极坐标(ρ≥0，0≤θ＜2π)．‎ 解：（Ⅰ）将消去参数t得 C1的普通方程为(x－4)2＋(y－5)2＝25‎ 即C1：x2＋y2－8x－10y＋16＝0‎ 将代入上式得 ρ2－8ρcosθ－10ρsinθ＋16＝0‎ ‎∴C1的极坐标方程为ρ2－8ρcosθ－10ρsinθ＋16＝0‎ ‎（Ⅱ）∵C2的极坐标方程为ρ＝2sinθ ‎∴C2的普通方程为x2＋y2－2y＝0‎ 由 ‎（此处为解方程的过程，可省略）‎ ‎②－①，得　8x＋8y－16＝0‎ 整理，得y＝2－x③‎ 把③代入②，得 x2＋(2－x)2－2(2－x)＝0‎ 整理，得x2－x＝0‎ ‎(特别注意，x是未知数，不能约去的)‎ 提取x，得x(x－1)＝0‎ ‎∴x＝0或x－1＝0‎ 解得x＝0或x＝1‎ 把x＝0代入③，得y＝2‎ 把x＝1代入③，得y＝1‎ 解得或 C1与C2交点的直角坐标分别为(0，2)，(1，1)‎ 对于点(0，2)有：ρ＝＝＝2，θ＝‎ 对于点(1，1)有：ρ＝＝＝，tanθ＝＝1，θ＝‎ ‎∴C1与C2交点的极坐标分别为(2，)，(，)‎ ‎【题型4】其它题型：．求交点坐标，求点的坐标，求轨迹方程等．‎ ‎9．（2015全国Ⅱ卷，文/理23，10分）在直角坐标系xOy中，曲线C1：(t为参数，t≠0)，其中0≤α＜π．在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ＝2sinθ，C3：ρ＝2cosθ．‎ ‎（Ⅰ）求C2与C3交点的直角坐标；‎ ‎（Ⅱ）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．‎ 解：（Ⅰ）∵C2：ρ＝2sinθ ‎∴ρ2＝2ρsinθ 把ρ2＝x2＋y2，y＝ρsinθ代入上式得 曲线C2的直角坐标方程为x2＋y2－2y＝0　①………………1分 9‎ ‎∵C3：ρ＝2‎3‎cosθ ‎∴ρ2＝2‎3‎ρcosθ 把ρ2＝x2＋y2，x＝ρcosθ代入上式得 曲线C3的直角坐标方程为x2＋y2－2x＝0　②………………2分 联立①②得………………3分 ‎（此处为解方程的过程，可省略）‎ ‎①－②，得　－2y＋2x＝0‎ 整理，得y＝x③‎ 把③代入①，得x2＋3x2－2x＝0‎ 整理，得2x2－x＝0‎ ‎(特别注意，x是未知数，不能约去的)‎ 提取x，得x(2x－)＝0‎ ‎∴x＝0或2x－＝0‎ 解得x＝0或x＝‎ 把x＝0代入③，得y＝0‎ 把x＝代入③，得y＝‎ 解得或………………4分 ‎∴C2与C3交点的直角坐标为(0，0)和‎3‎‎2‎‎，‎‎3‎‎2‎………………5分 ‎（Ⅱ）曲线C1的极坐标方程为θ＝α(ρ∈R，ρ≠0)，其中0≤α<π 因此A的极坐标为(2sinα，α)，B的极坐标为(2‎3‎cosα，α)‎ ‎∴|AB|＝|2sinα－2‎3‎cosα|＝4‎sinα－‎π‎3‎ 当α＝‎5π‎6‎时，|AB|取得最大值，最大值为4‎ ‎10．（2013全国Ⅱ卷，文/理23，10分）已知动点P，Q都在曲线C：(t为参数)上，对应参数分别为t＝α与t＝2α(0＜α＜2π)，M为PQ的中点．‎ ‎（Ⅰ）求M的轨迹的参数方程；‎ ‎（Ⅱ）将M到坐标原点的距离d表示为α的函数，并判断M的轨迹是否过坐标原点．‎ 解：（Ⅰ）∵动点P，Q都在曲线C：x＝2costy＝2sint(t为参数)上 ‎∴P(2cosα，2sinα)，Q(2cos2α，2sin2α)‎ ‎∵M为PQ的中点 ‎∴xM＝＝cosα＋cos2α yM＝＝sinα＋sin2α ‎∴M(cosα＋cos2α，sinα＋sin2α)．‎ ‎∴M的轨迹的参数方程为x＝cosα＋cos2α，‎y＝sinα＋sin2α(α为参数，0<α<2π)．‎ ‎（Ⅱ）M点到坐标原点的距离d＝x‎2‎‎＋‎y‎2‎‎＝‎‎2＋2cosα(0<α<2π)．‎ 当α＝π时，d＝0，故M的轨迹过坐标原点 9‎ ‎11．（2012全国卷，文/理23，10分）已知曲线C1的参数方程是(φ为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程是ρ＝2．正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为(2，)．‎ ‎（Ⅰ）求点A，B，C，D的直角坐标；‎ ‎（Ⅱ）设P为C1上任意一点，求|PA|2＋|PB|2＋|PC|2＋|PD|2的取值范围．‎ 解：（Ⅰ）∵点A的极坐标为‎2，‎π‎3‎ ‎∴点B的极坐标为‎2，π‎3‎＋‎π‎2‎ 点C的极坐标为‎2，π‎3‎＋π 点D的极坐标为‎2，π‎3‎＋‎‎3π‎2‎ ‎∴xA＝‎2cosπ‎3‎＝1，yA＝‎2sinπ‎3‎＝‎‎3‎ xB＝2cosπ‎3‎‎＋‎π‎2‎＝－‎3‎，yB＝2sinπ‎3‎‎＋‎π‎2‎＝1‎ xC＝2cosπ‎3‎＋π＝－1，yC＝2sinπ‎3‎＋π＝－‎‎3‎ xD＝2cosπ‎3‎‎＋‎‎3π‎2‎＝‎3‎，yD＝2sinπ‎3‎‎＋‎‎3π‎2‎＝－1‎ 即A(1，‎3‎)，B(－‎3‎，1)，C(－1，－‎3‎)，D(‎3‎，－1)‎ ‎（Ⅱ）设P(2cosφ，3sinφ)，‎ 令S＝|PA|2＋|PB|2＋|PC|2＋|PD|2‎ 则S＝16cos2φ＋36sin2φ＋16＝32＋20sin2φ ‎∵0≤sin2φ≤1‎ ‎∴S的取值范围是[32，52]‎ ‎12．（2011全国卷，文/理23，10分）在直角坐标系xOy中，曲线C1的参数方程为(α为参数)，M是C1上的动点，P点满足＝2，P点的轨迹为曲线C2．‎ ‎（Ⅰ）求C2的方程；‎ ‎（Ⅱ）在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ＝与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|．‎ 解：（Ⅰ）设P(x，y)，则由条件知M(，)．‎ 由于M点在C1上 ‎∴　即 从而C2的参数方程为(α为参数)‎ ‎（Ⅱ）曲线C1的极坐标方程为ρ＝4sinθ 曲线C2的极坐标方程为ρ＝8sinθ 9‎ 射线θ＝与C1的交点A的极径为ρ1＝4sin 射线θ＝与C2的交点B的极径为ρ2＝8sin ‎∴|AB|＝|ρ2－ρ1|＝2‎ ‎13．（2010全国卷，文/理23，10分）已知直线C1：（t为参数），圆C2：(θ为参数)．‎ ‎（Ⅰ）当α＝时，求C1与C2的交点坐标；‎ ‎（Ⅱ）过坐标原点O做C1的垂线，垂足为A，P为OA的中点，当α变化时，求P点轨迹的参数方程，并指出它是什么曲线．‎ 解：（Ⅰ）当α＝时 C1的普通方程为 C2的普通方程为 联立方程组 解得C1与C2的交点为（1，0），‎ ‎（Ⅱ）C1的普通方程为.‎ A点坐标为，‎ 故当变化时，P点轨迹的参数方程为 ‎（为参数）‎ P点轨迹的普通方程为 故P点是圆心为，半径为的圆 9‎