江苏高考立体几何含解析

江苏高考立体几何含解析

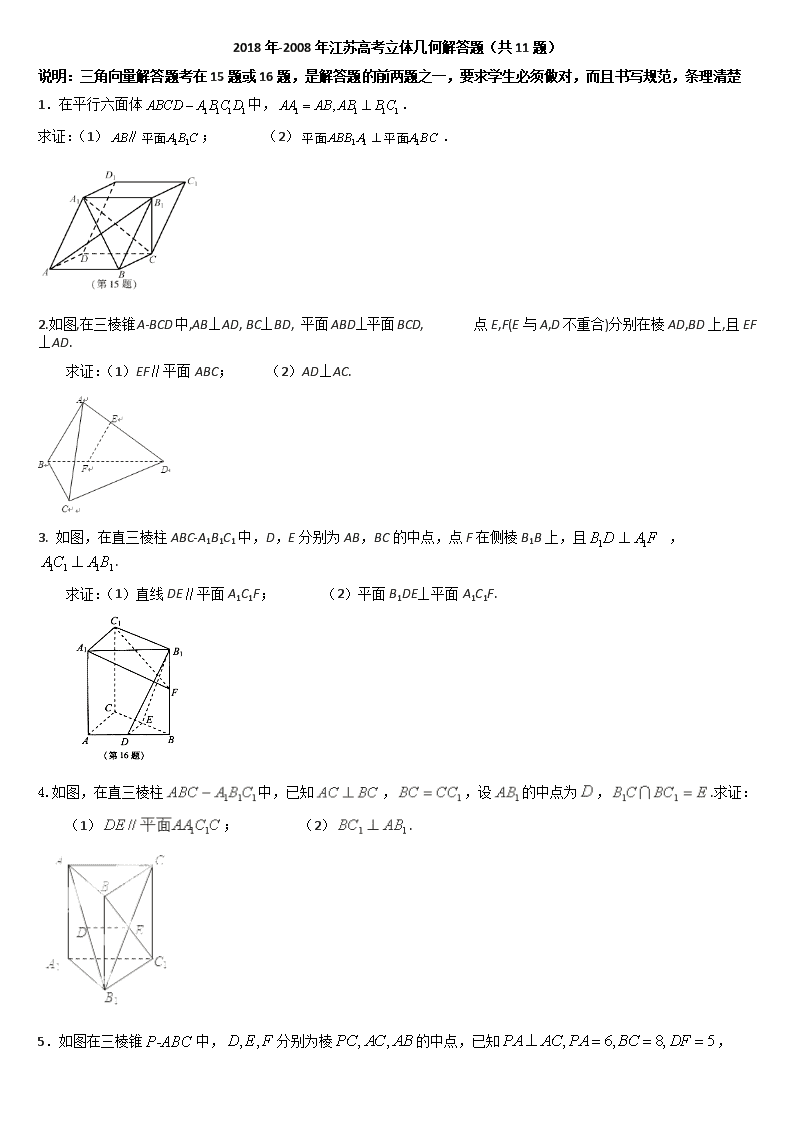
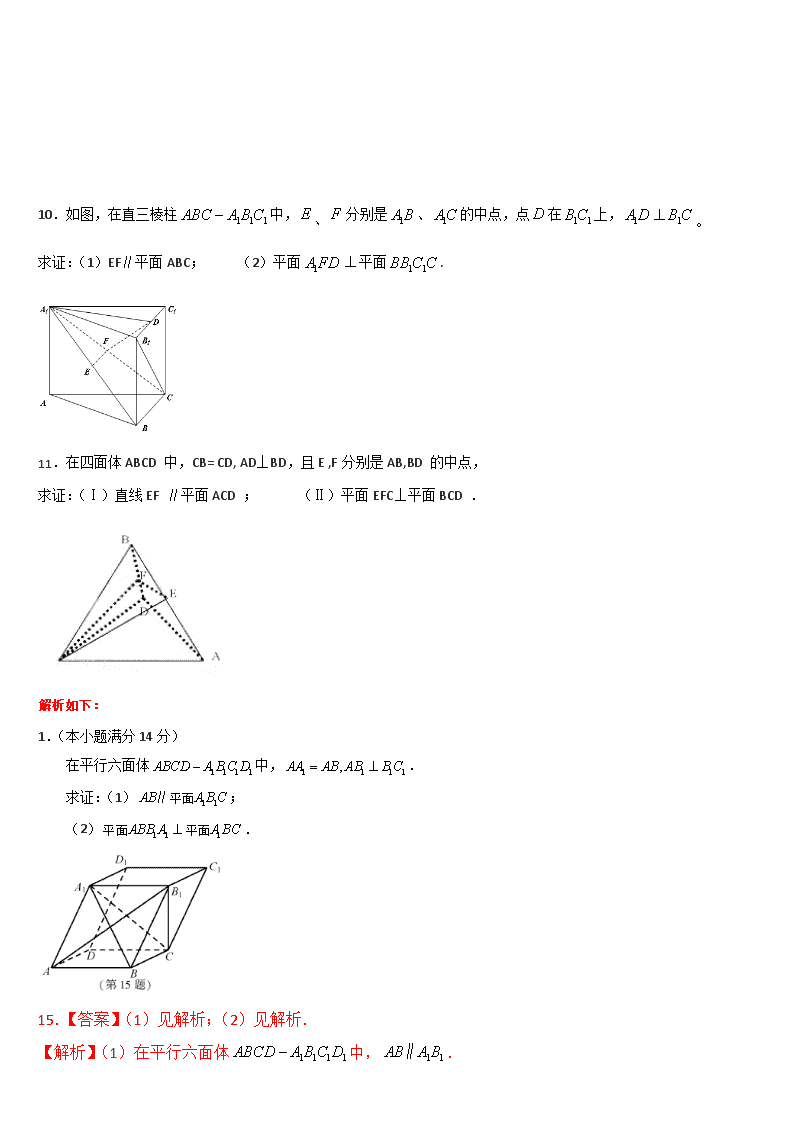
‎2018年-2008年江苏高考立体几何解答题（共11题）‎ 说明：三角向量解答题考在15题或16题，是解答题的前两题之一，要求学生必须做对，而且书写规范，条理清楚 1． 在平行六面体中，．‎ 求证：（1）； （2）．‎ ‎2.如图,在三棱锥A-BCD中,AB⊥AD, BC⊥BD, 平面ABD⊥平面BCD, 点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.‎ ‎ 求证：（1）EF∥平面ABC； （2）AD⊥AC.‎ ‎3. 如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且 ，.‎ 求证：（1）直线DE∥平面A1C1F； （2）平面B1DE⊥平面A1C1F. ‎ ‎4.如图，在直三棱柱中，已知，，设的中点为，.求证：‎ ‎（1）； （2）.‎ ‎5．如图在三棱锥中，分别为棱的中点，已知，‎ 求证（1）直线平面； （2）平面平面。‎ ‎6．如图，在三棱锥中，平面平面，，，过作，垂足为，点分别是棱的中点．求证：‎ ‎（1）平面平面； （2）．‎ ‎7. 如图，在直三棱柱中，，分别是棱上的点（点D 不同于点C），且为的中点．‎ 求证：（1）平面平面； （2）直线平面ADE．‎ ‎8、如图，在四棱锥中，平面PAD⊥平面ABCD，AB=AD，∠BAD=60°，E、F分别是AP、AD的中点 求证：（1）直线EF‖平面PCD；（2）平面BEF⊥平面PAD ‎9、如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。‎ (1) 求证：PC⊥BC； (2)求点A到平面PBC的距离。‎ ‎10．如图，在直三棱柱中，、分别是、的中点，点在上，。 ‎ 求证：（1）EF∥平面ABC；w.w.w.k.s.5.u.c.o.m （2）平面平面.‎ ‎11．在四面体ABCD 中，CB= CD, AD⊥BD，且E ,F分别是AB,BD 的中点，‎ 求证：（Ⅰ）直线EF ∥平面ACD ； （Ⅱ）平面EFC⊥平面BCD ．‎ 解析如下：‎ ‎1．（本小题满分14分）‎ 在平行六面体中，．‎ 求证：（1）；‎ （2） ‎．‎ ‎15．【答案】（1）见解析；（2）见解析．‎ ‎【解析】（1）在平行六面体中，．‎ 因为平面，平面，所以平面．‎ ‎（2）在平行六面体中，四边形为平行四边形．‎ 又因为，所以四边形为菱形，‎ 因此．又因为，，所以．‎ 又因为，平面，平面，‎ 所以平面．因为平面，‎ 所以平面平面．‎ ‎2.（本小题满分14分） 如图,在三棱锥A-BCD中,AB⊥AD, BC⊥BD, 平面ABD⊥平面BCD, 点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.‎ ‎ 求证：（1）EF∥平面ABC；‎ ‎ （2）AD⊥AC.‎ ‎【答案】（1）见解析（2）见解析 ‎【解析】证明：（1）在平面内，因为AB⊥AD，，所以.‎ ‎3. (本小题满分14分)‎ 如图，在直三棱柱ABC-A1B1C1中，D，E分别为AB，BC的中点，点F在侧棱B1B上，且 ，.‎ 求证：（1）直线DE∥平面A1C1F；‎ ‎（2）平面B1DE⊥平面A1C1F. ‎ ‎【答案】（1）详见解析（2）详见解析 ‎4.（本题满分14分）如图，在直三棱柱中，已知，，设的中点为，.求证：‎ ‎（1）； （2）.‎ ‎【答案】（1）详见解析（2）详见解析 ‎【解析】‎ 试题分析：（1）由三棱锥性质知侧面为平行四边形,因此点为的中点，从而由三角形中位线性质得，再由线面平行判定定理得（2）因为直三棱柱中，所以侧面为正方形，因此，又，（可由直三棱柱推导），因此由线面垂直判定定理得,从而，再由线面垂直判定定理得,进而可得 ‎5．（满分14分）如图在三棱锥中，分别为棱的中点，已知，‎ 求证（1）直线平面；‎ ‎（2）平面平面。‎ ‎ ‎ ‎6．如图，在三棱锥中，平面平面，，，过作，垂足为，点分别是棱的中点．求证：‎ ‎（1）平面平面；‎ ‎（2）．‎ 证：（1）因为SA＝AB且AF⊥SB，‎ 所以F为SB的中点．‎ 又E，G分别为SA，SC的中点，‎ 所以，EF∥AB，EG∥AC．‎ 又AB∩AC＝A，AB面SBC，AC面ABC，‎ 所以，平面平面．‎ ‎（2）因为平面SAB⊥平面SBC，平面SAB∩平面SBC＝BC，‎ AF平面ASB，AF⊥SB．‎ 所以，AF⊥平面SBC．‎ 又BC平面SBC，‎ 所以，AF⊥BC．‎ 又AB⊥BC，AF∩AB＝A，‎ 所以，BC⊥平面SAB．‎ 又SA平面SAB，‎ 所以，．‎ ‎7. 如图，在直三棱柱中，，分别是棱上的点（点D 不同于点C），且为的中点．‎ 求证：（1）平面平面；‎ ‎ （2）直线平面ADE．‎ ‎【答案及解析】‎ ‎【命题意图】本题主要考查直线与平面、平面与平面的位置关系，考查空间想象能力和推理论证能力.‎ ‎【证明】（1）∵是直棱柱， ∴⊥面ABC， ‎ ‎∵AD面ABC， ∴⊥AD，‎ ‎∵AD⊥DE，面，DE面，，‎ ‎∴AD⊥面， ∵AD面ADE， ∴面ADE⊥面.‎ ‎(2) ∵=，F为的中点， ∴⊥，‎ ‎∵⊥面，且面， ∴⊥，‎ ‎∵面，面，∩=，‎ ‎∴⊥面， 由（1）知，AD⊥面， ∴∥AD.‎ ‎∵AD面ADE，面ADE， ∴∥面ADE..‎ ‎8、（本小题满分14分）如图，在四棱锥中，平面PAD⊥平面ABCD，‎ AB=AD，∠BAD=60°，E、F分别是AP、AD的中点 求证：（1）直线EF‖平面PCD；‎ ‎（2）平面BEF⊥平面PAD 解析：简单考察空间想象能力和推理论证能力、线面平行和垂直的判定与性质，容易题。‎ ‎（1）因为E、F分别是AP、AD的中点，‎ 又 直线EF‖平面PCD ‎（2） F是AD的中点，‎ 又平面PAD⊥平面ABCD，‎ 所以，平面BEF⊥平面PAD。‎ ‎9、（本小题满分14分）如图，在四棱锥P-ABCD中，PD⊥平面ABCD，PD=DC=BC=1，AB=2，AB∥DC，∠BCD=900。‎ (1) 求证：PC⊥BC；‎ (2) 求点A到平面PBC的距离。‎ ‎[解析] 本小题主要考查直线与平面、平面与平面的位置关系，考查几何体的体积，考查空间想象能力、推理论证能力和运算能力。满分14分。‎ ‎（1）证明：因为PD⊥平面ABCD，BC平面ABCD，所以PD⊥BC。‎ 由∠BCD=900，得CD⊥BC，‎ 又PDDC=D，PD、DC平面PCD，‎ 所以BC⊥平面PCD。‎ 因为PC平面PCD，故PC⊥BC。‎ ‎（2）（方法一）分别取AB、PC的中点E、F，连DE、DF，则：‎ 易证DE∥CB，DE∥平面PBC，点D、E到平面PBC的距离相等。‎ 又点A到平面PBC的距离等于E到平面PBC的距离的2倍。‎ 由（1）知：BC⊥平面PCD，所以平面PBC⊥平面PCD于PC，‎ 因为PD=DC，PF=FC，所以DF⊥PC，所以DF⊥平面PBC于F。‎ 易知DF=，故点A到平面PBC的距离等于。‎ ‎（方法二）体积法：连结AC。设点A到平面PBC的距离为h。‎ 因为AB∥DC，∠BCD=900，所以∠ABC=900。‎ 从而AB=2，BC=1，得的面积。‎ 由PD⊥平面ABCD及PD=1，得三棱锥P-ABC的体积。‎ 因为PD⊥平面ABCD，DC平面ABCD，所以PD⊥DC。‎ 又PD=DC=1，所以。‎ 由PC⊥BC，BC=1，得的面积。‎ 由，，得，‎ 故点A到平面PBC的距离等于。‎ ‎10．（本小题满分14分） ‎ 如图，在直三棱柱中，、分别是、的中点，点在上，。 ‎ 求证：（1）EF∥平面ABC；w.w.w.k.s.5.u.c.o.m ‎ ‎（2）平面平面.‎ ‎【解析】 本小题主要考查直线与平面、平面与平面得位置关系，考查空间想象能力、推理论证能力。满分14分。‎ ‎11．在四面体ABCD 中，CB= CD, AD⊥BD，且E ,F分别是AB,BD 的中点，‎ 求证：（Ⅰ）直线EF ∥面ACD ；‎ ‎（Ⅱ）面EFC⊥面BCD ．‎ ‎【解析】本小题考查空间直线与平面、平面与平面的位置关系的判定．‎ 解：（Ⅰ）∵ E,F 分别是AB,BD 的中点，‎ ‎∴EF 是△ABD 的中位线，∴EF∥AD，‎ ‎∵EF面ACD ，AD 面ACD ，∴直线EF∥面ACD ．‎ ‎（Ⅱ）∵ AD⊥BD ，EF∥AD，∴ EF⊥BD.‎ ‎∵CB=CD, F 是BD的中点，∴CF⊥BD.‎ 又EFCF=F，∴BD⊥面EFC．∵BD面BCD，∴面EFC⊥面BCD ．‎