高考数学广东卷文科答案

高考数学广东卷文科答案

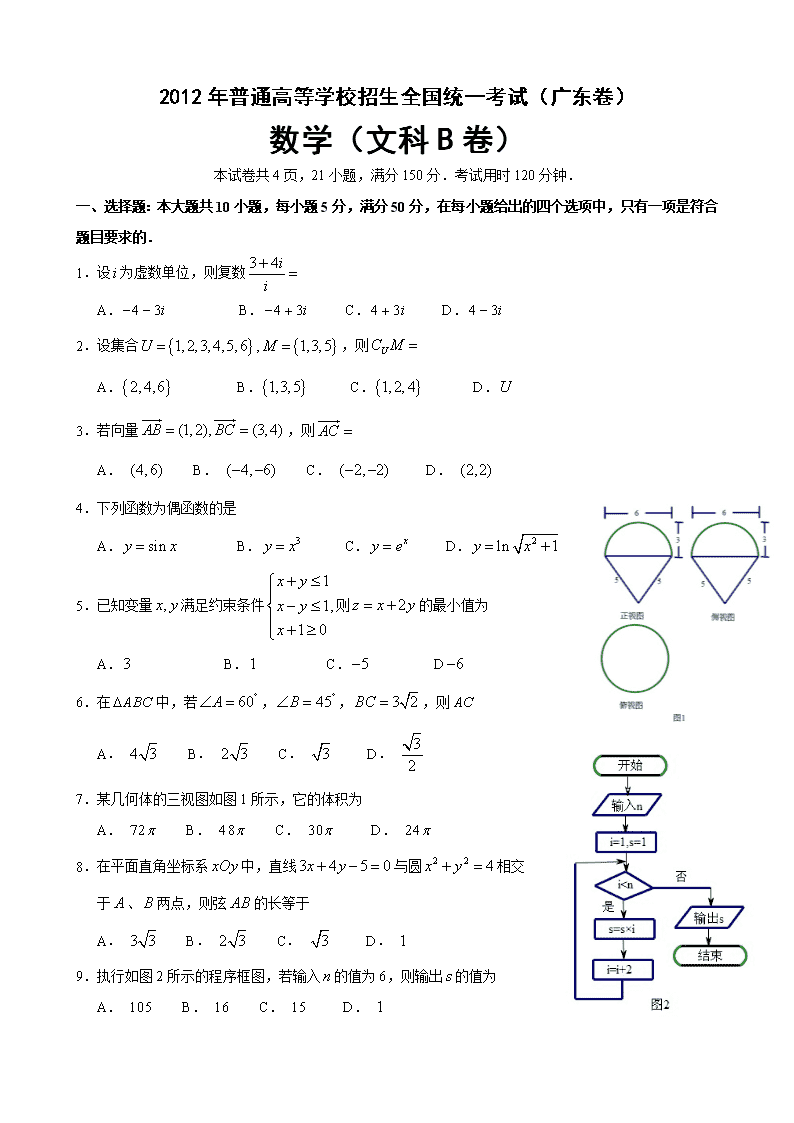
‎2012年普通高等学校招生全国统一考试（广东卷）‎ 数学（文科B卷）‎ 本试卷共4页，21小题，满分150分．考试用时120分钟．‎ 一、选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设为虚数单位，则复数 A． B． C． D．‎ ‎2．设集合,，则 A． B． C． D．‎ ‎3．若向量，则 ‎ A． B． C． D． ‎ ‎4．下列函数为偶函数的是 A． B． C． D．‎ ‎5．已知变量满足约束条件则的最小值为 A． B． C． D ‎6．在中，若，，，则 ‎ A． B． C． D． ‎ ‎7．某几何体的三视图如图1所示，它的体积为 ‎ A． B． C． D． ‎ ‎8．在平面直角坐标系中，直线与圆相交 于、两点，则弦的长等于 ‎ ‎ A． B． C． D． ‎ ‎9．执行如图2所示的程序框图，若输入的值为6，则输出的值为 ‎ ‎ A． B． C． D． ‎ ‎10．对任意两个非零的平面向量，定义．若平面向量满足，‎ 与的夹角，且和都在集合中，则 A． B． C． D． ‎ 二、填空题：本大题共5小题．考生作答4小题．每小题5分，满分20分． ‎ ‎（一）必做题（11～13题）‎ ‎11．函数的定义域为________________________．‎ ‎12．若等比数列满足，则_______________．‎ ‎13．由整数组成的一组数据其平均数和中位数都是2，且标准差等于1，则这组数据位_______________________．(从小到大排列)‎ ‎（二）选做题（14、15题，考生只能从中选做一题）‎ ‎14．（坐标系与参数方程选做题）‎ 在平面直角坐标系中中，曲线和曲线的 参数方程分别为（为参数，）和（为参数），则曲线和曲线的交点坐标为 ．‎ ‎15．（几何证明选讲选做题）‎ 如图3，直线PB与圆相切与点B，D是弦AC上的点，，若，则AB= ．‎ 图3‎ O A B C P D ‎·‎ 三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．‎ ‎16．（本小题满分12分）‎ 已知函数,且．‎ （1） 求的值；‎ （2） 设，，求的值．‎ ‎ ‎ ‎17．（本小题满分13分）‎ 某学校100名学生期中考试语文成绩的频率分布直方图如图4所示，其中成绩分组区间是：‎ ‎，，，，．‎ (1) 求图中a的值 (2) 根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ (3) 若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数 之比如下表所示，求数学成绩在之外的人数．‎ 分数段 x：y ‎1：1‎ ‎2：1‎ ‎3：4‎ ‎4：5‎ ‎18．（本小题满分13分）‎ 如图5所示，在四棱锥P-ABCD中,AB平面PAD,ABCD,PD=AD,E是PB的中点，F是DC上的点且DF=AB,PH为PAD中AD边上的高．‎ （1） 证明：PH平面ABCD；‎ （2） 若PH=1，AD=,FC=1，求三棱锥E-BCF的体积；‎ （3） 证明：EF平面PAB． ‎ ‎19．（本小题满分14分）‎ 设数列的前项和，数列的前项和为，满足．‎ （1） 求的值；‎ （2） 求数列的通项公式．‎ ‎20． （本小题满分14分）‎ 在平面直角坐标系中，已知椭圆的左焦点为，且点在上．‎ （1） 求椭圆的方程；‎ （2） 设直线与椭圆和抛物线相切，求直线的方程．‎ ‎21． （本小题满分14分）‎ 设，集合，，．‎ (1) 求集合（用区间表示）；‎ (2) 求函数在内的极值点．‎ ‎2012广东高考数学答案 ‎1-5 DAADC 6-10 BCBCD ‎11 ; 12 ; 13 ; 14 ; 15 ‎ ‎16. 解：（1），解得 ‎（2），即 ‎，即 ‎ 因为，所以，‎ ‎ 所以 ‎17. 解：（1）依题意得，，解得 ‎（2）这100名学生语文成绩的平均分为：（分）‎ ‎（3）数学成绩在的人数为：‎ 数学成绩在的人数为：‎ 数学成绩在的人数为：‎ 数学成绩在的人数为：‎ ‎ 所以数学成绩在之外的人数为：‎ ‎18. 解：（1）证明：因为平面， 所以 因为为△中边上的高 所以 ‎ 因为 所以平面 ‎（2）连结，取中点，连结 ‎ 因为是的中点， 所以 ‎ 因为平面 所以平面 则 ‎ ‎ ‎（3）证明：取中点，连结，‎ ‎ 因为是的中点 所以 因为 所以 所以四边形是平行四边形 所以 因为 所以 因为平面， 所以 ‎ 因为 所以平面 所以平面 ‎19. 解：（1）当时，‎ 因为，所以，求得 ‎（2）当时，‎ ‎ 所以 ①‎ ‎ 所以 ②‎ ‎ ②①得 ‎ ‎ 所以，即 ‎ 求得，，则 所以是以3为首项，2为公比的等比数列 ‎ 所以 ‎ 所以，‎ ‎20. 解：（1）因为椭圆的左焦点为，所以，‎ 点代入椭圆，得，即，‎ 所以 所以椭圆的方程为.‎ ‎（2）直线的斜率显然存在，设直线的方程为，‎ ‎，消去并整理得 因为直线与椭圆相切，所以 整理得 ①‎ ‎，消去并整理得 因为直线与抛物线相切，所以 整理得 ②‎ 综合①②，解得或 所以直线的方程为或 ‎21. 解：（1）令 ‎① 当时，，方程的两个根分别为，‎ 所以的解集为 因为，‎ 所以 ‎② 当时，，则恒成立，所以 综上所述，当时，；‎ 当时，‎ ‎（2），‎ ‎ 令，得或 ‎① 当时，由（1）知 因为，‎ 所以，‎ 所以随的变化情况如下表：‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ ‎↗‎ 所以的极大值点为，没有极小值点 ‎② 当时，由（1）知 所以随的变化情况如下表：‎ ‎0‎ ‎0‎ ‎↗‎ 极大值 ‎↘‎ 极小值 ‎↗‎ 所以的极大值点为，极小值点为 综上所述，当时，有一个极大值点，没有极小值点；‎ 当时，有一个极大值点，一个极小值点