- 2021-05-13 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
09—浙江高考真题文科数学分类汇编——立体几何
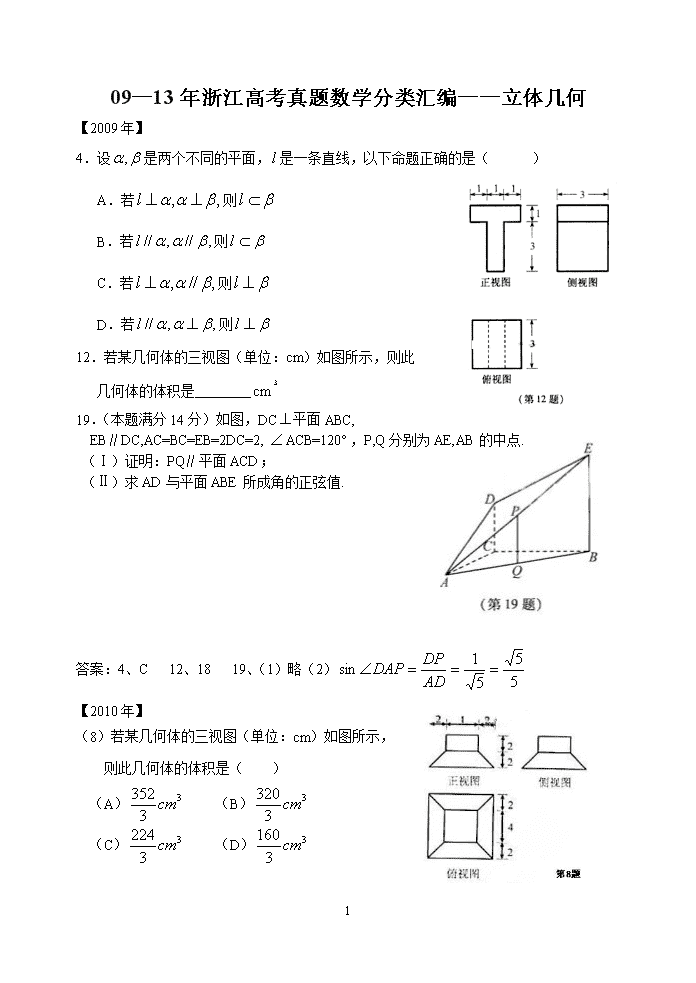
09—13年浙江高考真题数学分类汇编——立体几何 【2009年】 4.设是两个不同的平面,是一条直线,以下命题正确的是( ) A.若则 B.若则 C.若则 D.若则 12.若某几何体的三视图(单位:cm)如图所示,则此 几何体的体积是 19.(本题满分14分)如图,DC平面ABC, EB∥DC,AC=BC=EB=2DC=2,ACB=120°,P,Q分别为AE,AB的中点. (Ⅰ)证明:PQ∥平面ACD; (Ⅱ)求AD与平面ABE所成角的正弦值. 答案:4、C 12、18 19、(1)略(2) 【2010年】 (8)若某几何体的三视图(单位:cm)如图所示, 则此几何体的体积是( ) (A) (B) (C) (D) 5 (20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°, E为线段AB的中线,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点. (Ⅰ)求证:BF∥平面A′DE; (Ⅱ)设M为线段DE的中点,求直线FM与 平面A′DE所成角的余弦值. 2010年答案:8、B 20、(2) 2011年答案:4、B 7、B 20、(2) 【2011年】 (4)若直线不平行于平面,且,则( ) A.内的所有直线与异面 B.内不存在与平行的直线 C.内存在唯一的直线与平行 D.内的直线与都相交 (7)几何体的三视图如图所示,则这个几何体的直观图可以是( ) (20)(本题满分14分)如图,在三棱锥中,,为的中点,⊥平面,垂足落在线段上. (Ⅰ)证明:⊥; (Ⅱ)已知,,,.求二面角的大小. 5 【2012年】 3. 已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是( ) A.1cm³ B.2cm³ C.3cm³ D.6cm³ 5. 设是直线,是两个不同的平面,则( ) A.若,则 B.若,则 C.若,则 D.若,则 20. (本题满分15分)如图,在侧棱垂直底面的四棱柱中,, . ,是的中点,是平面与直线的交点。 (1)证明:①; ②平面; (2)求与平面所成的角的正弦值。 答案:3、A 5、B 20、(1)略(2). 5 【2013年】 4.设是两条不同的直线,a,β是两个不同的平面,则( ) A.若,则 B.若,则 C.若,则 D.若,则 5.已知某几何体的三视图(单位:cm)如图所示,则该三棱锥的体 积是( ) A.108cm3 B.100cm3 C.92cm3 D.84cm3 20. (本题满分15分)如图,在四棱锥P-ABCD中, PA⊥平面ABCD,AB=BC=2,AD=CD=, ,G是线段PC的点. (1)证明: BD⊥平面APC; (2)若G是线段PC的中点,求DG与平面APC所成的 角的正切值; (3)若G满足PC⊥平面BGD,求的值。 5 答案: 4、C 5、B 20、(2) (3) 2014年 3、某几何体的三视图(单位:cm)如图所示,则该几何体的的体积是( ) 4 4 3 3 3 3 正视图 侧视图 俯视图 A.72 cm3 B.90 cm3 C.108 cm3 D.138 cm3 20、如图,在四棱锥A—BCDE中,平面平面;,,,。 (1)证明:平面; (2)求直线与平面ABC所成的角的正切值。 5查看更多