山东高考数学理科解答题答案

山东高考数学理科解答题答案

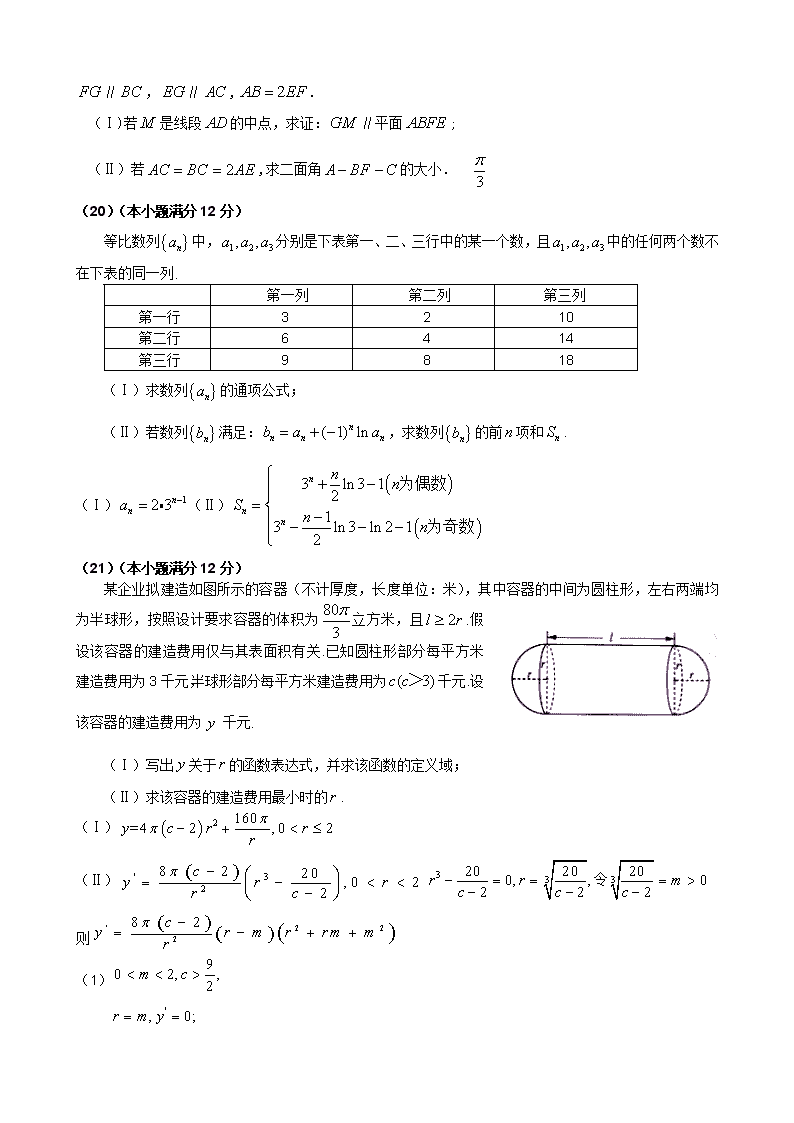
‎2011年普通高等学校招生全国统一考试（山东卷）‎ 理 科 数 学 参考公式：‎ 柱体的体积公式：，其中表示柱体的底面积，表示柱体的高.‎ 圆柱的侧面积公式：，其中c是圆柱的底面周长，是圆柱的母线长.‎ 球的体积公式V=, 其中是球的半径.‎ 球的表面积公式：,其中是球的半径.‎ 用最小二乘法求线性回归方程系数公式 .‎ 如果事件互斥，那么.‎ 解答题：本大题共6小题，共74分.‎ ‎（17）（本小题满分12分）‎ 在中，内角，，的对边分别为，，.已知.‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）若 ，求的面积.‎ ‎（Ⅰ） （Ⅱ）‎ ‎（18）（本小题满分12分）‎ 红队队员甲、乙、丙与蓝队队员、、进行围棋比赛，甲对，乙对，丙对各一盘，已知甲胜，乙胜，丙胜的概率分别为0.6,0.5,0.5，假设各盘比赛结果相互独立.‎ ‎（Ⅰ）求红队至少两名队员获胜的概率；‎ ‎（Ⅱ）用表示红队队员获胜的总盘数，求的分布列和数学期望.‎ ‎（Ⅰ）0.55 （Ⅱ）1.6‎ A B C D E F G M ‎（19）（本小题满分12分）‎ 在如图所 示的几何体中，四边形为平行四边形，‎ ‎，⊥平面，∥，‎ ‎∥，∥,.‎ ‎（Ⅰ)若是线段的中点，求证：∥平面;‎ ‎（Ⅱ）若,求二面角的大小． ‎ ‎（20）（本小题满分12分）‎ 等比数列中，分别是下表第一、二、三行中的某一个数，且中的任何两个数不在下表的同一列.‎ 第一列 第二列 第三列 第一行 ‎3‎ ‎2‎ ‎10‎ 第二行 ‎6‎ ‎4‎ ‎14‎ 第三行 ‎9‎ ‎8‎ ‎18‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若数列满足：，求数列的前项和.‎ ‎（Ⅰ）（Ⅱ）‎ ‎（21）（本小题满分12分）‎ 某企业拟建造如图所示的容器（不计厚度，长度单位：米），其中容器的中间为圆柱形，左右两端均为半球形，按照设计要求容器的体积为立方米，且.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元，半球形部分每平方米建造费用为千元.设该容器的建造费用为千元.‎ ‎（Ⅰ）写出关于的函数表达式，并求该函数的定义域；‎ ‎（Ⅱ）求该容器的建造费用最小时的.‎ ‎（Ⅰ）‎ ‎（Ⅱ）‎ 则 ‎（1）‎ 所以，是极小值点，也是最小值点 ‎（2）当时，当，函数单调递减，所以，是函数最小值点。‎ 综上，时，费用最小时；时，费用最小时.‎ ‎（22）（本小题满分14分）‎ 已知直线与椭圆: 交于,两不同点，且的面积S=,其中为坐标原点。‎ ‎（Ⅰ）证明和均为定值 ‎（Ⅱ）设线段的中点为，求的最大值；‎ ‎（Ⅲ）椭圆上是否存在点, , ，使得？若存在，判断的形状；若不存在，请说明理由.‎ ‎（Ⅰ）直线斜率不存在时，；‎ 直线斜率存在时，，显然，代入椭圆方程整理得 由 ‎，‎ 由,得 ∴；.‎ ‎（Ⅱ）, ∴的最大值是 ‎（Ⅲ）不存在。‎