高考数学考前必看系列材料之一基本知识篇1

高考数学考前必看系列材料之一基本知识篇1

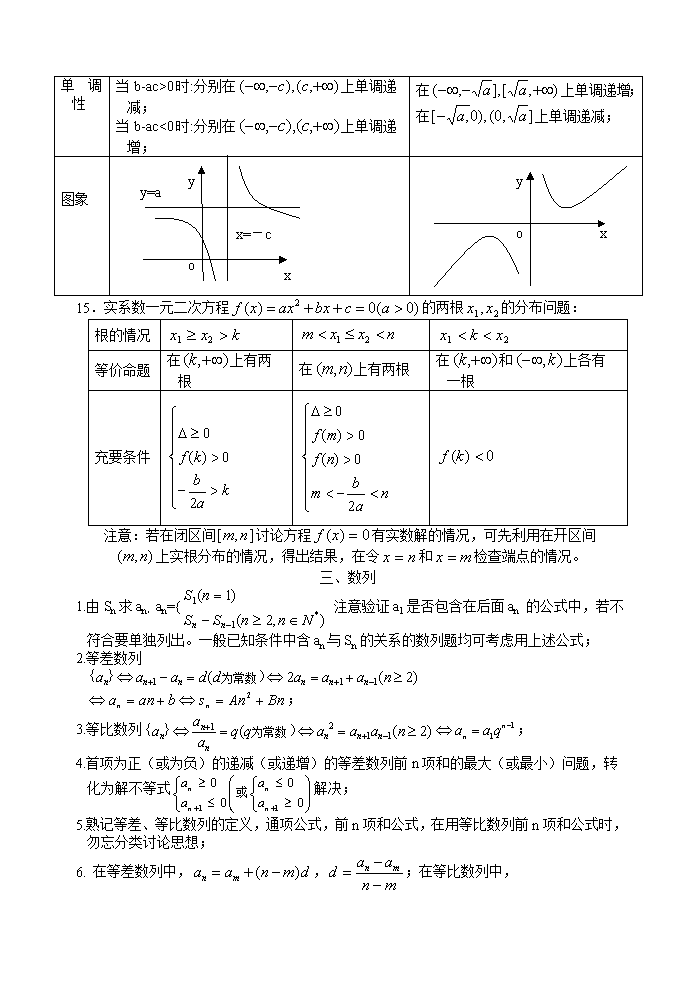
高考数学考前必看系列材料之一 基本知识篇 一、集合与简易逻辑 ‎1.研究集合问题，一定要抓住集合的代表元素，如：与及 ‎2.数形结合是解集合问题的常用方法，解题要尽可能地借助数轴、直角坐标系或韦恩图等工具，将抽象的代数问题具体化、形象化、直观化，然后利用数形结合的思想方法解决；‎ ‎3.一个语句是否为命题，关键要看能否判断真假，陈述句、反诘问句都是命题，而祁使句、疑问句、感叹句都不是命题；‎ ‎4.判断命题的真假要以真值表为依据。原命题与其逆否命题是等价命题 ，逆命题与其否命题是等价命题 ，一真俱真，一假俱假，当一个命题的真假不易判断时，可考虑判断其等价命题的真假；‎ ‎5.判断命题充要条件的三种方法：（1）定义法；（2）利用集合间的包含关系判断，若，则A是B的充分条件或B是A的必要条件；若A=B，则A是B的充要条件；（3）等价法：即利用等价关系判断，对于条件或结论是不等关系（或否定式）的命题，一般运用等价法；‎ ‎6.（1）含n个元素的集合的子集个数为，真子集（非空子集）个数为－1；‎ ‎（2） （3）‎ 二、函数 ‎1.复合函数的有关问题 ‎（1）复合函数定义域求法：若已知的定义域为［a，b］,其复合函数f[g(x)]的定义域由不等式a≤g(x)≤b解出即可；若已知f[g(x)]的定义域为[a,b],求 f(x)的定义域，相当于x∈[a,b]时，求g(x)的值域（即 f(x)的定义域）；研究函数的问题一定要注意定义域优先的原则。‎ ‎（2）复合函数的单调性由“同增异减”判定；‎ ‎2.函数的奇偶性 ‎（1）若f(x)是偶函数，那么f(x)=f(－x)=;‎ ‎（2）若f(x)是奇函数，0在其定义域内，则（可用于求参数）；‎ ‎（3）判断函数奇偶性可用定义的等价形式：f(x)±f(-x)=0或（f(x)≠0）;‎ ‎ (4)若所给函数的解析式较为复杂，应先化简，再判断其奇偶性；‎ ‎（5）奇函数在对称的单调区间内有相同的单调性；偶函数在对称的单调区间内有相反的单调性；‎ ‎3.函数图像（或方程曲线的对称性）‎ ‎(1)证明函数图像的对称性，即证明图像上任意点关于对称中心（对称轴）的对称点仍在图像上；‎ ‎（2）证明图像C1与C2的对称性，即证明C1上任意点关于对称中心（对称轴）的对称点仍在C2上，反之亦然；‎ ‎（3）曲线C1：f(x,y)=0,关于y=x+a(y=-x+a)的对称曲线C2的方程为f(y－a,x+a)=0(或f(－y+a,－x+a)=0);‎ ‎（4）曲线C1:f(x,y)=0关于点（a,b）的对称曲线C2方程为：f(2a－x,2b－y)=0;‎ ‎（5）若函数y=f(x)对x∈R时，f(a+x)=f(a－x)恒成立，则y=f(x)图像关于直线x=a对称；‎ ‎（6）函数y=f(x－a)与y=f(b－x)的图像关于直线x=对称；‎ ‎4.函数的周期性 ‎(1)y=f(x)对x∈R时，f(x +a)=f(x－a) 或f(x－2a )=f(x) (a>0)恒成立,则y=f(x)是周期为2a的周期函数；‎ ‎（2）若y=f(x)是偶函数，其图像又关于直线x=a对称，则f(x)是周期为2︱a︱的周期函数；‎ ‎（3）若y=f(x)奇函数，其图像又关于直线x=a对称，则f(x)是周期为4︱a︱的周期函数；‎ ‎（4）若y=f(x)关于点(a,0),(b,0)对称，则f(x)是周期为2的周期函数；‎ ‎（5）y=f(x)的图象关于直线x=a,x=b(a≠b)对称，则函数y=f(x)是周期为2的周期函数；‎ ‎（6）y=f(x)对x∈R时，f(x+a)=－f(x)(或f(x+a)= ，则y=f(x)是周期为2的周期函数；‎ ‎5.方程k=f(x)有解k∈D(D为f(x)的值域)；‎ ‎6.a≥f(x) 恒成立a≥［f(x)］max,; a≤f(x) 恒成立a≤［f(x)］min;‎ ‎7.（1） (a>0,a≠1,b>0,n∈R+); (2) l og a N=( a>0,a≠1,b>0,b≠1);‎ ‎(3) l og a b的符号由口诀“同正异负”记忆; (4) a log a N= N ( a>0,a≠1,N>0 );‎ ‎8.能熟练地用定义证明函数的单调性，求反函数，判断函数的奇偶性。‎ ‎9.判断对应是否为映射时，抓住两点：（1）A中元素必须都有象且唯一；（2）B中元素不一定都有原象，并且A中不同元素在B中可以有相同的象；‎ ‎10.对于反函数，应掌握以下一些结论：（1）定义域上的单调函数必有反函数；（2）奇函数的反函数也是奇函数；（3）定义域为非单元素集的偶函数不存在反函数;（4）周期函数不存在反函数；（5）互为反函数的两个函数具有相同的单调性；(5) y=f(x)与y=f-1(x)互为反函数，设f(x)的定义域为A，值域为B，则有f[f-－1(x)]=x(x∈B),f-－1[f(x)]=x(x∈A).‎ ‎11.处理二次函数的问题勿忘数形结合；二次函数在闭区间上必有最值，求最值问题用“两看法”：一看开口方向；二看对称轴与所给区间的相对位置关系；‎ ‎12.恒成立问题的处理方法：（1）分离参数法；（2）转化为一元二次方程的根的分布列不等式(组)求解；‎ ‎13.依据单调性，利用一次函数在区间上的保号性可解决求一类参数的范围问题：(或（或）；‎ ‎14.掌握函数的图象和性质；‎ 函数 ‎(b – ac≠0)‎ ‎）‎ 定义域 值域 奇偶性 非奇非偶函数 奇函数 单调性 当b-ac>0时:分别在上单调递减；‎ 当b-ac<0时:分别在上单调递增；‎ 在上单调递增；‎ 在上单调递减；‎ 图象 y x o x=－c y=a x y o ‎15．实系数一元二次方程的两根的分布问题：‎ 根的情况 等价命题 在上有两根 在上有两根 在和上各有一根 充要条件 注意：若在闭区间讨论方程有实数解的情况，可先利用在开区间上实根分布的情况，得出结果，在令和检查端点的情况。‎ 三、数列 ‎1.由Sn求an，an={ 注意验证a1是否包含在后面an 的公式中，若不符合要单独列出。一般已知条件中含an与Sn的关系的数列题均可考虑用上述公式；‎ ‎2.等差数列；‎ ‎3.等比数列； ‎ ‎4.首项为正（或为负）的递减（或递增）的等差数列前n项和的最大（或最小）问题，转化为解不等式解决；‎ ‎5.熟记等差、等比数列的定义，通项公式，前n项和公式，在用等比数列前n项和公式时，勿忘分类讨论思想；‎ ‎6. 在等差数列中，，；在等比数列中，‎ ‎;‎ ‎7. 当时，对等差数列有；对等比数列有；‎ ‎8.若{an}、{bn}是等差数列，则{kan+pbn}(k、p是非零常数)是等差数列；若{an}、{bn}是等比数列，则｛kan｝、{anbn}等也是等比数列；‎ ‎9. 若数列为等差（比）数列，则也是等差（比）数列；‎ ‎10. 在等差数列中，当项数为偶数时，；项数为奇数时，（即）； ‎ ‎11.若一阶线性递归数列an=kan－1+b（k≠0,k≠1）,则总可以将其改写变形成如下形式:(n≥2)，于是可依据等比数列的定义求出其通项公式；‎ 四、三角函数 ‎1.三角函数符号规律记忆口诀：一全正，二正弦，三是切，四余弦；‎ ‎2.对于诱导公式，可用“奇变偶不变，符号看象限”概括；‎ ‎3.记住同角三角函数的基本关系，熟练掌握三角函数的定义、图像、性质；‎ ‎4.熟知正弦、余弦、正切的和、差、倍公式，正余弦定理，处理三角形内的三角函数问题勿忘三内角和等于1800，一般用正余弦定理实施边角互化；‎ ‎5.正(余)弦型函数的对称轴为过最高点或最低点且垂直于轴的直线，对称中心为图象与轴的交点；正(余)切型函数的对称中心是图象和渐近线分别与轴的交点，但没有对称轴。‎ ‎6.（1）正弦平方差公式：sin‎2A－sin2B=sin(A+B)sin(A－B);（2）三角形的内切圆半径r=；（3）三角形的外接圆直径2R=‎ 五、平面向量 ‎1.两个向量平行的充要条件,设a=(x1,y1),b=(x2,y2),为实数。（1）向量式：a∥b(b≠0)a=b;（2）坐标式：a∥b(b≠0)x1y2－x2y1=0;‎ ‎2.两个向量垂直的充要条件, 设a=(x1,y1),b=(x2,y2), （1）向量式：a⊥b(b≠0)ab=0; （2）坐标式：a⊥bx1x2+y1y2=0;‎ ‎3.设a=(x1,y1),b=(x2,y2),则ab==x1x2+y1y2;其几何意义是ab等于a的长度与b在a的方向上的投影的乘积；‎ ‎4.设A（x1,x2）、B(x2,y2)，则S⊿AOB＝；‎ ‎5.平面向量数量积的坐标表示：‎ ‎（1）若a=(x1,y1),b=(x2,y2),则ab=x1x2+y1y2;;‎ ‎（2）若a=(x,y),则a2=aa=x2+y2,;‎ 六、不等式 ‎1.掌握不等式性质，注意使用条件；‎ ‎2.掌握几类不等式（一元一次、二次、绝对值不等式、简单的指数、对数不等式）的解法，尤其注意用分类讨论的思想解含参数的不等式；勿忘数轴标根法，零点分区间法；‎ ‎3.掌握用均值不等式求最值的方法，在使用a+b≥(a>0,b>0)时要符合“一正二定三相等”；注意均值不等式的一些变形，如；‎ 七、直线和圆的方程 ‎1.设三角形的三顶点是A（x1,y1）、B(x2,y2)、C（x3,y3）,则⊿ABC的重心G为（）；‎ ‎2.直线l1:A1x+B1y+C1=0与l2: A2x+B2y+C2=0垂直的充要条件是A1A2+B1B2=0；‎ ‎3.两条平行线Ax+By+C1=0与 Ax+By+C2=0的距离是；‎ ‎4.Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的充要条件 ：A=C≠0且B=0且D2+E2－4AF>0；‎ ‎5.过圆x2+y2=r2上的点M(x0,y0)的切线方程为：x0x+y0y=r2;‎ ‎6.以A(x1，y2)、B(x2,y2)为直径的圆的方程是(x－x1)(x－x2)+(y－y1)(y－y2)=0;‎ ‎7.求解线性规划问题的步骤是：（1）根据实际问题的约束条件列出不等式；（2）作出可行域，写出目标函数；（3）确定目标函数的最优位置，从而获得最优解；‎ 八、圆锥曲线方程 ‎1.椭圆焦半径公式：设P（x0,y0）为椭圆（a>b>0）上任一点，焦点为F1(-c,0),F2(c,0),则（e为离心率）；‎ ‎2.双曲线焦半径公式：设P（x0,y0）为双曲线（a>0,b>0）上任一点，焦点为F1(-c,0),F2(c,0),则:（1）当P点在右支上时，；‎ ‎（2）当P点在左支上时，；（e为离心率）；‎ 另：双曲线（a>0,b>0）的渐近线方程为；‎ ‎3.抛物线焦半径公式：设P（x0,y0）为抛物线y2=2px(p>0)上任意一点，F为焦点，则；y2=2px(p＜0)上任意一点，F为焦点，则；‎ ‎4.涉及圆锥曲线的问题勿忘用定义解题；‎ ‎5.共渐进线的双曲线标准方程为为参数，≠0）；‎ ‎6.计算焦点弦长可利用上面的焦半径公式，‎ 一般地，若斜率为k的直线被圆锥曲线所截得的弦为AB， A、B两点分别为A(x1，y1)、B(x2,y2)，则弦长 ‎ ‎,这里体现了解析几何“设而不求”的解题思想；‎ ‎7.椭圆、双曲线的通径（最短弦）为，焦准距为p=，抛物线的通径为2p，焦准距为p; 双曲线（a>0，b>0）的焦点到渐进线的距离为b;‎ ‎8.中心在原点，坐标轴为对称轴的椭圆，双曲线方程可设为Ax2+Bx2＝1；‎ ‎9.抛物线y2=2px(p>0)的焦点弦（过焦点的弦）为AB，A（x1,y1）、B(x2,y2),则有如下结论：（1）＝x1+x2+p;（2）y1y2=－p2，x1x2=;‎ ‎10.过椭圆（a>b>0）左焦点的焦点弦为AB，则，过右焦点的弦；‎ ‎11.对于y2=2px(p≠0)抛物线上的点的坐标可设为（，y0）,以简化计算;‎ ‎12.处理椭圆、双曲线、抛物线的弦中点问题常用代点相减法，设A(x1，y1)、B(x2,y2)为椭圆（a>b>0）上不同的两点，M(x0,y0)是AB的中点，则KABKOM=；对于双曲线（a>0，b>0），类似可得：KAB.KOM=；对于y2=2px(p≠0)抛物线有KAB＝‎ ‎13.求轨迹的常用方法：‎ ‎（1）直接法：直接通过建立x、y之间的关系，构成F(x,y)＝0，是求轨迹的最基本的方法；‎ ‎（2）待定系数法：所求曲线是所学过的曲线：如直线，圆锥曲线等，可先根据条件列出所求曲线的方程，再由条件确定其待定系数，代回所列的方程即可；‎ ‎（3）代入法（相关点法或转移法）：若动点P(x,y)依赖于另一动点Q(x1,y1)的变化而变化，并且Q(x1,y1)又在某已知曲线上，则可先用x、y的代数式表示x1、y1，再将x1、y1带入已知曲线得要求的轨迹方程；‎ ‎（4）定义法：如果能够确定动点的轨迹满足某已知曲线的定义，则可由曲线的定义直接写出方程；‎ ‎（5）参数法：当动点P（x,y）坐标之间的关系不易直接找到，也没有相关动点可用时，可考虑将x、y均用一中间变量（参数）表示，得参数方程，再消去参数得普通方程。‎ 九、直线、平面、简单几何体 ‎1.从一点O出发的三条射线OA、OB、OC，若∠AOB=∠AOC，则点A在平面∠BOC上的射影在∠BOC的平分线上；‎ A ‎2. 已知:直二面角M－AB－N中，AE M，BF N,∠EAB=,∠ABF=，异面直线AE与BF所成的角为，则 ‎3.立平斜公式：如图，AB和平面所成的角是，AC在平面内，AC和AB的射影AB成，设∠BAC=,则coscos=cos；‎ ‎4.异面直线所成角的求法：‎ ‎（1）平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；‎ ‎（2）补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；‎ ‎5.直线与平面所成的角 斜线和平面所成的是一个直角三角形的锐角，它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影。通常通过斜线上某个特殊点作出平面的垂线段，垂足和斜足的连线，是产生线面角的关键；‎ ‎6.二面角的求法 ‎（1）定义法：直接在二面角的棱上取一点（特殊点），分别在两个半平面内作棱的垂线，得出平面角，用定义法时，要认真观察图形的特性；‎ ‎（2）三垂线法：已知二面角其中一个面内一点到一个面的垂线，用三垂线定理或逆定理作出二面角的平面角；‎ ‎（3）垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个半平面的交线所成的角即为平面角，由此可知，二面角的平面角所在的平面与棱垂直；‎ ‎（4）射影法：利用面积射影公式S射＝S原cos,其中为平面角的大小，此方法不必在图形中画出平面角；‎ 特别:对于一类没有给出棱的二面角，应先延伸两个半平面，使之相交出现棱，然后再选用上述方法（尤其要考虑射影法）。‎ ‎7.空间距离的求法 ‎（1）两异面直线间的距离，高考要求是给出公垂线，所以一般先利用垂直作出公垂线，然后再进行计算；‎ ‎（2）求点到直线的距离，一般用三垂线定理作出垂线再求解；‎ ‎（3）求点到平面的距离，一是用垂面法，借助面面垂直的性质来作，因此，确定已知面的垂面是关键；二是不作出公垂线，转化为求三棱锥的高，利用等体积法列方程求解；‎ ‎8.正棱锥的各侧面与底面所成的角相等，记为，则S侧cos=S底；‎ ‎9.已知:长方体的体对角线与过同一顶点的三条棱所成的角分别为因此有cos2+cos2+cos2=1; 若长方体的体对角线与过同一顶点的三侧面所成的角分别为则有cos2+cos2+cos2=2;‎ ‎10.正方体和长方体的外接球的直径等与其体对角线长；‎ ‎11.欧拉公式：如果简单多面体的顶点数为V,面数为F,棱数为E.那么V+F－E=2；并且棱数E＝各顶点连着的棱数和的一半＝各面边数和的一半；‎ ‎12.球的体积公式V=，表面积公式；掌握球面上两点A、B间的距离求法：（1）计算线段AB的长，（2）计算球心角∠AOB的弧度数；(3)用弧长公式计算劣弧AB的长；‎ 十、排列组合二项式定理和概率 ‎1.排列数公式:=n(n-1)(n-2)…(n-m＋1)=(m≤n,m、n∈N*),当m=n时为全排列=n(n-1)…21;‎ ‎2.组合数公式：（m≤n）,；‎ ‎3.组合数性质：；‎ ‎4.常用性质：n.n!=(n+1)!-n!;即（1≤r≤n）;‎ ‎5.二项式定理：（1）掌握二项展开式的通项：‎ ‎（2）注意第r＋1项二项式系数与第r＋1系数的区别；‎ ‎6.二项式系数具有下列性质：‎ (1) 与首末两端等距离的二项式系数相等；‎ (2) 若n为偶数，中间一项（第＋1项）的二项式系数最大；若n为奇数，中间两项（第和 ‎＋1项）的二项式系数最大；‎ ‎（3）‎ ‎7.F(x)=(ax+b)n展开式的各项系数和为f(1);奇数项系数和为；偶数项的系数和为；‎ ‎8.等可能事件的概率公式：（1）P（A）＝；（2）互斥事件分别发生的概率公式为：P(A+B)=P(A)+P(B)；（3）相互独立事件同时发生的概率公式为P(AB)＝P(A)P(B)；（4）独立重复试验概率公式Pn(k)=(5)如果事件A、B互斥，那么事件A与、与及事件与也都是互斥事件；（6）如果事件A、B相互独立，那么事件A、B至少有一个不发生的概率是1－P（AB）＝1－P(A)P(B)；（7）如果事件A、B相互独立，那么事件A、B至少有一个发生的概率是1－P（）＝1－P()P()；‎ 十一、抽样方法、总体分布的估计与总体的期望和方差 ‎1.掌握抽样的二种方法：（1）简单随机抽样（包括抽签符和随机数表法）；（2）分层抽样，常用于某个总体由差异明显的几部分组成的情形；‎ ‎2.总体分布的估计：用样本估计总体，是研究统计问题的一个基本思想方法，一般地，样本容量越大，这种估计就越精确，要求能画出频率分布表和频率分布直方图；‎ ‎3.总体特征数的估计：（1）学会用样本平均数去估计总体平均数；（2）学会用样本去估计总体方差及总体标准差； ‎ 十二、导数及应用 ‎1.导数的定义：f(x)在点x0处的导数记作；‎ ‎2.根据导数的定义，求函数的导数步骤为：（1）求函数的增量(2)求平均变化率;(3)取极限,得导数;‎ ‎3.导数的几何意义：曲线y＝f（x）在点P（x0,f(x0)）处的切线的斜率是相应地，切线方程是 ‎4.常见函数的导数公式：‎ ‎5.导数的应用：（1）利用导数判断函数的单调性：设函数y＝f（x）在某个区间内可导，如果那么f(x)为增函数；如果那么f(x)为减函数；如果在某个区间内恒有那么f(x)为常数；‎ ‎（2）求可导函数极值的步骤：①求导数；②求方程的根；③检验在方程根的左右的符号，如果左正右负，那么函数y=f(x)在这个根处取得最大值；如果左负右正，那么函数y=f(x)在这个根处取得最小值；‎ ‎（3）求可导函数最大值与最小值的步骤：①求y=f(x)在(a,b)内的极值；②将y=f(x)在各极值点的极值与f（a）、f（b）比较，其中最大的一个为最大值，最小的一个是最小值。‎