- 2021-05-13 发布 |
- 37.5 KB |
- 8页
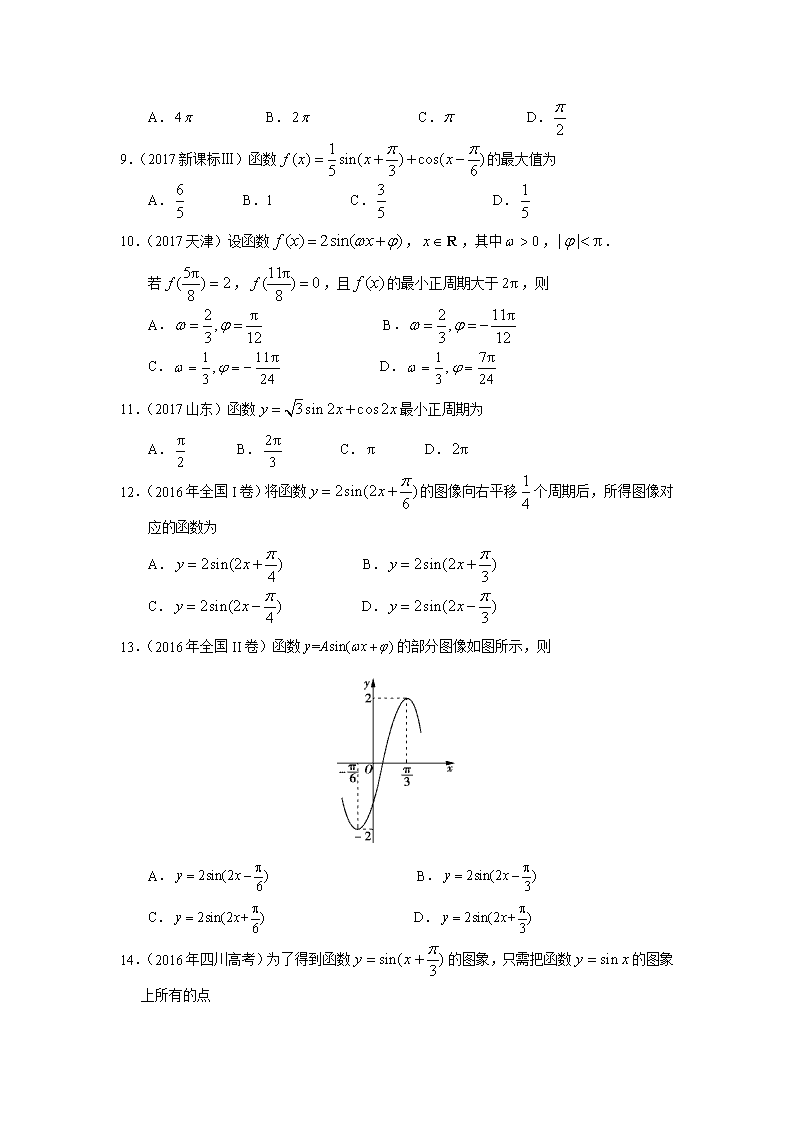
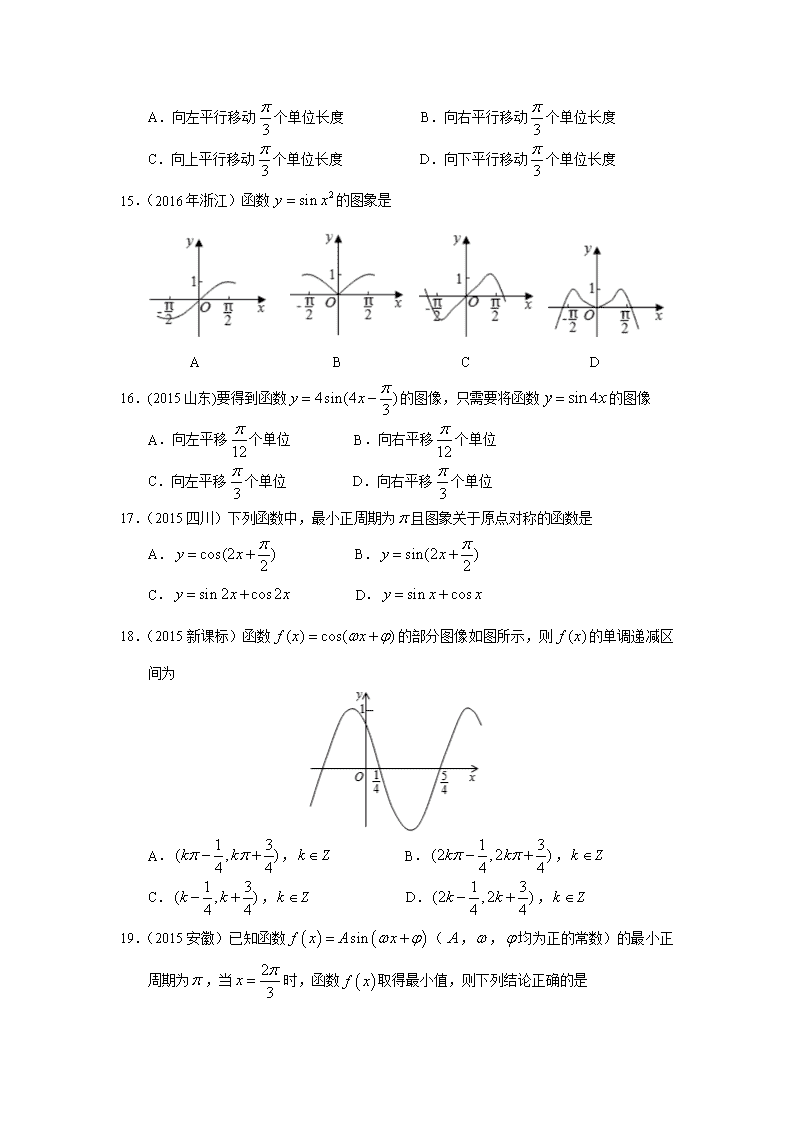
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三角函数高考专题练习
三角函数高考题 一、选择题 1.(2017新课标Ⅲ)已知,则= A. B. C. D. 2.(2017山东)已知,则 A. B. C. D. 3.(2016年全国III卷)若,则= A. B. C. D. 4.(2015重庆)若,,则 A. B. C. D. 5.(2015福建)若,且为第四象限角,则的值等于 A. B. C. D. 6.(2014新课标1)若,则 A. B. C. D. 7.(2017新课标Ⅰ)函数的部分图像大致为 8.(2017新课标Ⅱ)函数的最小正周期为 A. B. C. D. 9.(2017新课标Ⅲ)函数的最大值为 A. B.1 C. D. 10.(2017天津)设函数,,其中,. 若,,且的最小正周期大于,则 A. B. C. D. 11.(2017山东)函数最小正周期为 A. B. C. D. 12.(2016年全国I卷)将函数的图像向右平移个周期后,所得图像对应的函数为 A. B. C. D. 13.(2016年全国II卷)函数的部分图像如图所示,则 A. B. C. D. 14.(2016年四川高考)为了得到函数的图象,只需把函数的图象上所有的点 A.向左平行移动个单位长度 B.向右平行移动个单位长度 C.向上平行移动个单位长度 D.向下平行移动个单位长度 15.(2016年浙江)函数的图象是 A B C D 16.(2015山东)要得到函数的图像,只需要将函数的图像 A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位 17.(2015四川)下列函数中,最小正周期为且图象关于原点对称的函数是 A. B. C. D. 18.(2015新课标)函数的部分图像如图所示,则的单调递减区间为 A., B., C., D., 19.(2015安徽)已知函数(,,均为正的常数)的最小正周期为,当时,函数取得最小值,则下列结论正确的是 A. B. C. D. 20.(2014新课标1)在函数①,②,③,④中,最小正周期为的所有函数为 A.①②③ B.①③④ C.②④ D.①③ 21.(2017新课标Ⅰ)的内角、、的对边分别为、、.已知 ,,,则= A. B. C. D. 22.(2016全国I)△ABC的内角A、B、C的对边分别为a、b、c.已知,, ,则= A. B. C.2 D.3 23.(2016全国III)在中,,边上的高等于,则 A. B. C. D. 24.(2016山东)中,角A,B,C的对边分别是a,b,c,已知,则A= A. B. C. D. 25.(2015广东)设的内角的对边分别为,,.若,,,且,则 A. B. C. D. 26.(2014新课标2)钝角三角形的面积是,,,则= A.5 B. C.2 D.1 二、填空题 1.(2017新课标Ⅰ)已知,,则 =__________. 2.(2017北京)在平面直角坐标系中,角与角均以Ox为始边,它们的终边关于y轴对称.若sin=,则sin=_________. 3.(2017江苏)若,则= . 4.(2016年全国Ⅰ卷)已知是第四象限角,且,则 . 5.(2015四川)13.已知,则的值是________. 6.(2015江苏)已知,,则的值为_______. 7.(2017新课标Ⅱ)函数的最大值为 . 8.(2016全国Ⅲ卷)函数的图像可由函数的图像至少向右平移______个单位长度得到. 9.(2015浙江)函数的最小正周期是________,单调递减区间是_______. 10.(2015江苏)函数是常数,的部分图象如图所示,则f(0)= . 11.(2017新课标Ⅱ)的内角,,的对边分别为,,,若 ,则_________ 12.(2017新课标Ⅲ)的内角,,的对边分别为,,.已知,,,则=_________. 三.解答题 1.(2017天津)在中,内角所对的边分别为.已知 ,. (Ⅰ)求的值; (Ⅱ)求的值. 2.(2017山东)在中,角A,B,C的对边分别为a,b,c,已知, ,,求和. 3.(2015新课标2)中,D是BC上的点,AD平分∠BAC,∆ABD面积是∆ADC面积的2倍. (Ⅰ)求 ; (Ⅱ) 若AD=1,DC=,求BD和AC的长. 4.(2015新课标1)已知分别是内角的对边,. (Ⅰ)若,求 (Ⅱ)若,且,求的面积. 5.(15北京文科)已知函数. (Ⅰ)求的最小正周期; (Ⅱ)求在区间上的最小值. 6.(15年广东文科)已知. 求的值; 求的值. 7.(15年安徽文科)已知函数 (1)求最小正周期; (2)求在区间上的最大值和最小值. 8.(15年福建文科)已知函数. (Ⅰ)求函数的最小正周期; (Ⅱ)将函数的图象向右平移个单位长度,再向下平移()个单位长度后得到函数的图象,且函数的最大值为2.求函数的解析式; 9.(15年江苏)在中,已知. (1)求的长; (2)求的值. 10.(15年陕西文科)的内角所对的边分别为,向量与平行. (I)求; (II)若求的面积. 11.(15年天津文科)△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为, (I)求a和sinC的值; (II)求 的值 12.(2014·江苏卷) 已知α∈,sin α=. (1)求sin的值; (2)求cos的值. 13.(2014·四川卷17) 已知函数 (Ⅰ)求的单调递增区间; (Ⅱ)若是第二象限角,,求的值。 14.(2014·广东卷16) 已知函数f(x)=Asin,x∈R,且f=. (1)求A的值; (2)若f(θ)-f(-θ)=,θ∈,求f. 15.(2014·北京卷16) 函数f(x)=3sin的部分图像如图所示. (1)写出f(x)的最小正周期及图中x0,y0的值; (2)求f(x)在区间上的最大值和最小值. 16.(2015·福建卷) 已知函数f(x)=2cos x(sin x+cos x). (1)求f的值; (2)求函数f(x)的最小正周期及单调递增区间. 17. (2014·湖北卷18) 某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:f(t)=10-cost-sint,t∈[0,24). (1)求实验室这一天上午8时的温度; (2)求实验室这一天的最大温差. . 查看更多