高中数学必修15知识点高考复习总结

高中数学必修15知识点高考复习总结

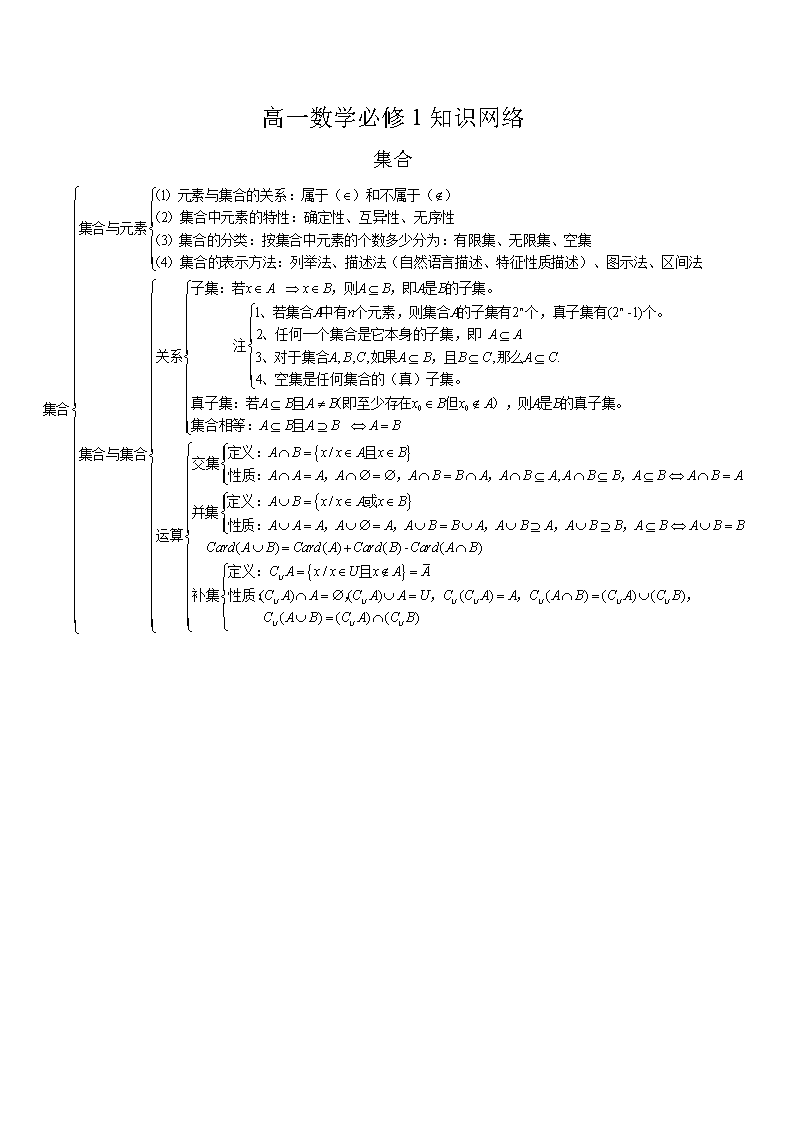
高一数学必修 1 知识网络 集合 1 2 3 4 1 2n x A x B A B A B A n A ∈ ∉    ∈ ⇒ ∈ ⊆ （）元素与集合的关系：属于（ ）和不属于（ ） （ ）集合中元素的特性：确定性、互异性、无序性集合与元素 （ ）集合的分类：按集合中元素的个数多少分为：有限集、无限集、空集 （ ）集合的表示方法：列举法、描述法（自然语言描述、特征性质描述）、图示法、区间法 子集：若 ，则 ，即 是 的子集。 、若集合 中有 个元素，则集合 的子集有 个， 注关系 集合 集合与集合 { } 0 0 (2 -1) 2 3 , , , , . 4 / n A A A B C A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B     ⊆  ⊆ ⊆ ⊆    ⊆ ≠ ∈ ∉ ⊆ ⊇ ⇔ = ∩ = ∈ ∈ ∩ = ∩∅ = ∅ ∩ = ∩ ∩ ⊆ 真子集有 个。 、任何一个集合是它本身的子集，即 、对于集合 如果 ，且 那么 、空集是任何集合的（真）子集。 真子集：若 且 （即至少存在 但 ），则 是 的真子集。 集合相等： 且 定义： 且交集 性质： ， ， ， 运算 { } { } , / ( ) ( ) ( ) - ( ) / ( ) ( ) ( ) ( ) ( ) ( ) U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B  ∩ ⊆ ⊆ ⇔ ∩ =  ∪ = ∈ ∈ ∪ = ∪∅ = ∪ = ∪ ∪ ⊇ ∪ ⊇ ⊆ ⇔ ∪ = ∪ = + ∩ = ∈ ∉ = ∩ = ∅ ∪ = = ∩ = ∪ ， 定义： 或并集 性质： ， ， ， ， ， 定义： 且 补集 性质： ， ， ， ， ( ) ( ) ( )U U UC A B C A C B                                            ∪ = ∩  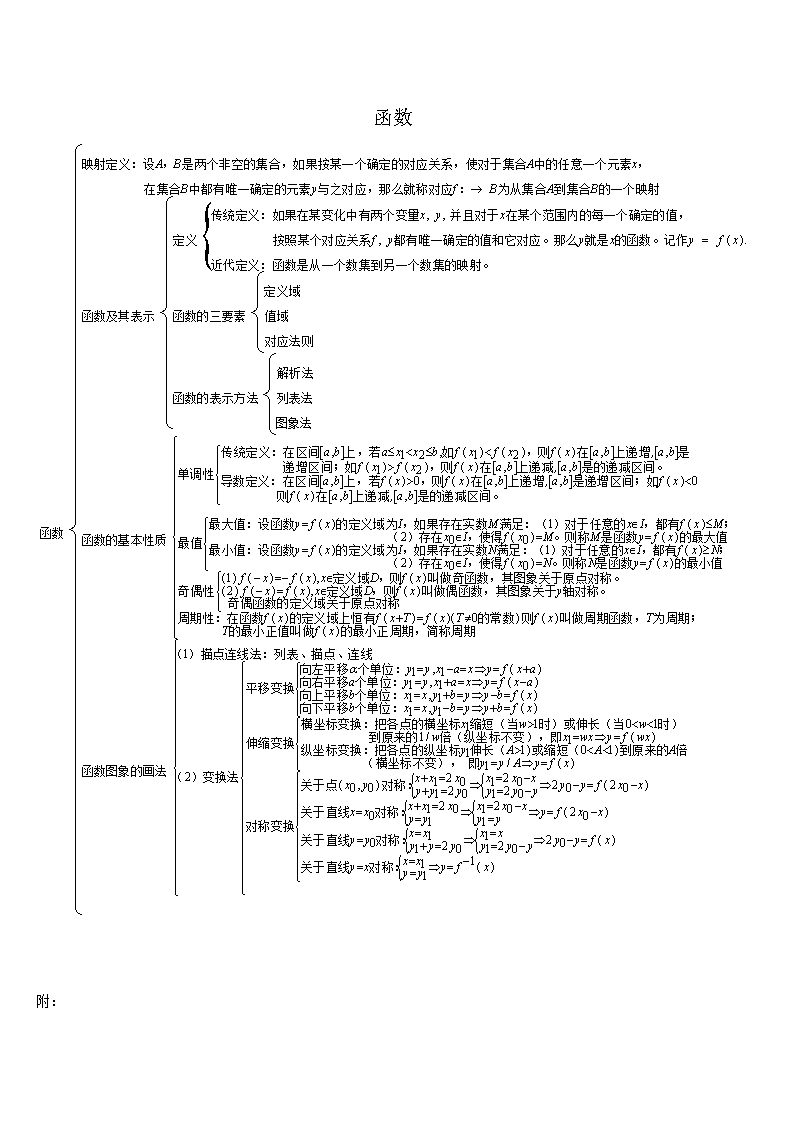函数 附： , , , A B A x B y f B A B x y x f y y x y → 映射定义：设 ， 是两个非空的集合，如果按某一个确定的对应关系，使对于集合 中的任意一个元素 ， 在集合 中都有唯一确定的元素 与之对应，那么就称对应 ： 为从集合 到集合 的一个映射 传统定义：如果在某变化中有两个变量 并且对于 在某个范围内的每一个确定的值， 定义 按照某个对应关系 都有唯一确定的值和它对应。那么 就是 的函数。记作 函数及其表示 函数 { [ ] [ ] [ ] [ ] [ ] ( ). , , ( ) ( ) ( ) , ,1 2 1 2 ( ) ( ) ( ) , ,1 2 f x a b a x x b f x f x f x a b a b f x f x f x a b a b a = ≤ < ≤ < >          近代定义：函数是从一个数集到另一个数集的映射。 定义域 函数的三要素 值域 对应法则 解析法 函数的表示方法 列表法 图象法 单调性 函数的基本性质 传统定义：在区间 上，若 如 ，则 在 上递增, 是 递增区间；如 ，则 在 上递减, 是的递减区间。 导数定义：在区间[ ] [ ] [ ] [ ] [ ] ( ) 1 ( ) 2 ( ) ( )0 0 , ( ) 0 ( ) , , ( ) 0 ( ) , , y f x I M x I f x M x I f x M M y f x b f x f x a b a b f x f x a b a b = ∈ ≤ ∈ = =   > <  最大值：设函数 的定义域为 ，如果存在实数 满足：（ ）对于任意的 ，都有 ； （ ）存在 ，使得 。则称 是函数 的最大值最值 最 上，若 ，则 在 上递增, 是递增区间；如 则 在 上递减, 是的递减区间。 ( ) 1 ( ) 2 ( ) ( )0 0 (1) ( ) ( ), ( ) (2) ( ) ( ), ( ) y f x I N x I f x N x I f x N N y f x f x f x x D f x f x f x x D f x = ∈ ≥ ∈ = = − =− ∈ − = ∈      小值：设函数 的定义域为 ，如果存在实数 满足：（ ）对于任意的 ，都有 ； （ ）存在 ，使得 。则称 是函数 的最小值 定义域 ，则 叫做奇函数，其图象关于原点对称。 奇偶性 定义域 ，则 叫做偶函数，其图 ( ) ( ) ( )( 0 ) ( ) ( ) 1 , ( )1 1 2 y f x f x T f x T f x T T f x y y x a x y f x a a α + = ≠ = − = ⇒ = +                   象关于 轴对称。 奇偶函数的定义域关于原点对称 周期性：在函数 的定义域上恒有 的常数 则 叫做周期函数， 为周期； 的最小正值叫做 的最小正周期，简称周期 （ ）描点连线法：列表、描点、连线 向左平移 个单位： 向右平移 个平移变换 函数图象的画法 （ ）变换法 , ( )1 1 , ( )1 1 , ( )1 1 1 0 11 1/ ( )1 1) 0 1)1 y y x a x y f x a b x x y b y y b f x b x x y b y y b f x x w w w x wx y f wx y A A = + = ⇒ = − = + = ⇒ − = = − = ⇒ + = > < < = ⇒ = > < <      单位： 向上平移 个单位： 向下平移 个单位： 横坐标变换：把各点的横坐标 缩短（当 时）或伸长（当 时） 到原来的 倍（纵坐标不变），即伸缩变换 纵坐标变换：把各点的纵坐标 伸长（ 或缩短（ 到 { { { { { { / ( )1 2 21 0 1 0( , ) 2 (2 )0 0 0 02 21 0 1 0 2 21 0 1 0 (2 )0 01 1 1 1 2 (0 02 21 0 1 0 A y y A y f x x x x x x xx y y y f x xy y y y y y x x x x x xx x y f x xy y y y x x x xy y y y fy y y y y y = ⇒ = + = = −⇒ ⇒ − = −+ = = − + = = −= ⇒ ⇒ = −= = = == ⇒ ⇒ − =+ = = −      原来的 倍 （横坐标不变）， 即 关于点 对称： 关于直线 对称： 对称变换 关于直线 对称： { ) 11 ( )1 x x xy x y f xy y = −= ⇒ ==                                                              关于直线 对称： 一、函数的定义域的常用求法： 1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函数和对数函数的底 数大于零且不等于 1；5、三角函数正切函数 中 ；余切函数 中；6、如果函数是 由实际意义确定的解析式，应依据自变量的实际意义确定其取值范围。 二、函数的解析式的常用求法： 1、定义法；2、换元法；3、待定系数法；4、函数方程法；5、参数法；6、配方法 三、函数的值域的常用求法： 1、换元法；2、配方法；3、判别式法；4、几何法；5、不等式法；6、单调性法；7、直接法 四、函数的最值的常用求法： 1、配方法；2、换元法；3、不等式法；4、几何法；5、单调性法 五、函数单调性的常用结论： 1、若 均为某区间上的增（减）函数，则 在这个区间上也为增（减）函数 2、若 为增（减）函数，则 为减（增）函数 3、若 与 的单调性相同，则 是增函数；若 与 的单调性不同，则 是减函 数。 4、奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相反。 5、常用函数的单调性解答：比较大小、求值域、求最值、解不等式、证不等式、作函数图象。 六、函数奇偶性的常用结论： 1、如果一个奇函数在 处有定义，则 ，如果一个函数 既是奇函数又是偶函数，则 （反 之不成立） 2、两个奇（偶）函数之和（差）为奇（偶）函数；之积（商）为偶函数。 3、一个奇函数与一个偶函数的积（商）为奇函数。 4、两个函数 和 复合而成的函数，只要其中有一个是偶函数，那么该复合函数就是偶函数；当两个 函数都是奇函数时，该复合函数是奇函数。 5、若函数 的定义域关于原点对称，则 可以表示为 ，该式的特 点是：右端为一个奇函数和一个偶函数的和。 tany x= ( )2x k k Z ππ≠ + ∈ coty x= ( ), ( )f x g x ( ) ( )f x g x+ ( )f x ( )f x− ( )f x ( )g x [ ( )]y f g x= ( )f x ( )g x [ ( )]y f g x= 0x = (0) 0f = ( )y f x= ( ) 0f x = ( )y f u= ( )u g x= ( )f x ( )f x 1 1( ) [ ( ) ( )] [ ( ) ( )]2 2f x f x f x f x f x= + − + − − , ( ) 0 ( ) ( ) [ , ] ( ) ( ) 0, ( ) [ , ] ( , ), ( ) 0, ( ) 0 ( ) 0 y f x f x x y f x y f x a b f a f b y f x a b c a b f c c f x f x = = = = ⋅ < = ∈ = = = 零点：对于函数 （ ）我们把使 的实数 叫做函数 的零点。 定理：如果函数 在区间 上的图象是连续不断的一条曲线，并且有 零点与根的关系 那么，函数 在区间 内有零点。即存在 使得 这个 也是方 程 的根。（反之不成立） 关系：方程 函数与方程 函数的应用 ( ) ( ) (1) [ , ], ( ) ( ) 0, (2) ( , ) ; (3) ( ) ( ) 0, ( ) ( ) 0, ( , )0 ( ) ( ) 0, 0 y f x y f x x a b f a f b a b c f c f c c f a f c b c x a b f c f b a c x ε ⇔ = ⇔ = ⋅ < = ⋅ < = ∈ ⋅ < =      有实数根 函数 有零点 函数 的图象与 轴有交点 确定区间 验证 给定精确度 ； 求区间 的中点 计算 ； 二分法求方程的近似解 ①若 则 就是函数的零点； ②若 则令 （此时零点 ）； ③若 则令 （此时零点 ( , ) (4) - , ( ); 2 4 c b a b a bε ε ∈ < ∼                    ）； 判断是否达到精确度 ：即若 则得到零点的近似值 或 否则重复 。 几类不同的增长函数模型 函数模型及其应用 用已知函数模型解决问题 建立实际问题的函数模型 , ( 0, , ) ( ) ( 0, , ) ( ) ( 0, 0, ) ( 0 1) 1 lo mn a n a n m na a r s r sa a a a r s Q r s rsa a a r s Q r r sab a b a b r Q xy a a a x = += > ∈ = > ∈ = > > ∈ = > ≠ =                    根 式 ： 为 根 指 数 ， 为 被 开 方 数 分 数 指 数 幂 指 数 的 运 算 指 数 函 数 性 质 定 义 ： 一 般 地 把 函 数 且 叫 做 指 数 函 数 。指 数 函 数 性 质 ： 见 表 对 数 ： 基 本 初 等 函 数 对 数 的 运 算 对 数 函 数 g , log ( ) log log ; log log log ; . log log ; ( 0, 1, 0, 0 ) log log ( 0 1) 1 log ( , 0 , 1, 0)log c a c N a Na M N M Na a a M M Na a aN nM n M a a M Na a y x a aa bb a c a c ba ⋅ = + = − = > ≠ > > = > ≠                = > ≠ >     为 底 数 ， 为 真 数 性 质 换 底 公 式 ： 定 义 ： 一 般 地 把 函 数 且 叫 做 对 数 函 数 对 数 函 数 性 质 ： 见 表 且 y x xα α                              =   幂 函 数 定 义 ： 一 般 地 ， 函 数 叫 做 幂 函 数 ， 是 自 变 量 ， 是 常 数 。 性 质 ： 见 表 2 表 1 指数函数 对数数函数 定义域 值域 图象 过定点 过定点 减函数 增函数 减函数 增函数 性质 ( )0, 1xy a a a= > ≠ ( )log 0, 1ay x a a= > ≠ x R∈ ( )0,x∈ +∞ ( )0,y∈ +∞ y R∈ (0,1) (1,0) ( ,0) (1, ) (0, ) (0,1) x y x y ∈ −∞ ∈ +∞ ∈ +∞ ∈ 时， 时， ( ,0) (0,1) (0, ) (1, ) x y x y ∈ −∞ ∈ ∈ +∞ ∈ +∞ 时， 时， (0,1) (0, ) (1, ) ( ,0) x y x y ∈ ∈ +∞ ∈ +∞ ∈ −∞ 时， 时， (0,1) ( ,0) (1, ) (0, ) x y x y ∈ ∈ −∞ ∈ +∞ ∈ +∞ 时， 时， a b< a b> a b< a b> 表 2 幂函数 奇函数 偶函数 第一象限性质 减函数 增函数 过定点 ( )y x Rα α= ∈ p q α = 0α < 0 1α< < 1α > 1α = p q 为奇数 为奇数 p q 为奇数 为偶数 p q 为偶数 为奇数 01（ ，） 高中数学必修 2 知识点 一、直线与方程 （1）直线的倾斜角 定义：x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地，当直线与 x 轴平行或重合时,我们规定它的倾 斜角为 0 度。因此，倾斜角的取值范围是 0°≤α＜180° （2）直线的斜率 ①定义：倾斜角不是 90°的直线，它的倾斜角的正切叫做这条直线的斜率。直线的斜率常用 k 表示。即 。斜 率反映直线与轴的倾斜程度。 当 时， ； 当 时， ； 当 时， 不存在。 ②过两点的直线的斜率公式： 注意下面四点：(1)当 时，公式右边无意义，直线的斜率不存在，倾斜角为 90°； (2)k 与 P1、P2 的顺序无关；(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得； (4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。 （3）直线方程 ①点斜式： 直线斜率 k，且过点 注意：当直线的斜率为 0°时，k=0，直线的方程是 y=y1。 当直线的斜率为 90°时，直线的斜率不存在，它的方程不能用点斜式表示．但因 l 上每一点的横坐标都等于 x1，所以 它的方程是 x=x1。 ②斜截式： ，直线斜率为 k，直线在 y 轴上的截距为 b ③两点式： （ ）直线两点 ， ④截矩式： 其中直线 与 轴交于点 ,与 轴交于点 ,即 与 轴、 轴的截距分别为 。 ⑤一般式： （A，B 不全为 0） 注意：○1 各式的适用范围 ○2 特殊的方程如： 平行于 x 轴的直线： （b 为常数）； 平行于 y 轴的直线： （a 为常数）； （5）直线系方程：即具有某一共同性质的直线 （一）平行直线系 平行于已知直线 （ 是不全为 0 的常数）的直线系： （C 为常数） （二）过定点的直线系 （ⅰ）斜率为 k 的直线系： ，直线过定点 ； （ⅱ）过两条直线 ， 的交点的直线系方程为 （ 为参数），其中直线 不在直线系中。 （6）两直线平行与垂直 当 ， 时， ； 注意：利用斜率判断直线的平行与垂直时，要注意斜率的存在与否。 （7）两条直线的交点 相交 tank α= [ ) 90,0∈α 0≥k ( ) 180,90∈α 0−+ FED      −− 2,2 ED FEDr 42 1 22 −+= 0422 =−+ FED 0422 <−+ FED 0: =++ CByAxl ( ) ( ) 222: rbyaxC =−+− ( )baC , 22 BA CBbAad + ++= 相离与Clrd ⇔> 相切与Clrd ⇔= 相交与Clrd ⇔< 0: =++ CByAxl ( ) ( ) 222: rbyaxC =−+− ∆ 相离与Cl⇔<∆ 0 相切与Cl⇔=∆ 0 相交与Cl⇔>∆ 0 2 00 ryyxx =+ ( )00 , yx 2 00 ryyxx =+ ( ) ( ) 22 1 2 11 : rbyaxC =−+− ( ) ( ) 22 2 2 22 : RbyaxC =−+− rRd +> rRd += rRdrR +<<− rRd −= rRd −< 0=d 三、立体几何初步 1、柱、锥、台、球的结构特征 （1）棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所 围成的几何体。 分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。 表示：用各顶点字母，如五棱柱 或用对角线的端点字母，如五棱柱 几何特征：两底面是对应边平行的全等多边形；侧面、对角面都是平行四边形；侧棱平行且相等；平行于底面的截面 是与底面全等的多边形。 （2）棱锥 定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体 分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等 表示：用各顶点字母，如五棱锥 几何特征：侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。 （3）棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分 分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等 表示：用各顶点字母，如五棱台 几何特征：①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点 （4）圆柱：定义：以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体 几何特征：①底面是全等的圆；②母线与轴平行；③轴与底面圆的半径垂直；④侧面展开图是一个矩形。 （5）圆锥：定义：以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体 几何特征：①底面是一个圆；②母线交于圆锥的顶点；③侧面展开图是一个扇形。 （6）圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分 几何特征：①上下底面是两个圆；②侧面母线交于原圆锥的顶点；③侧面展开图是一个弓形。 （7）球体：定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体 几何特征：①球的截面是圆；②球面上任意一点到球心的距离等于半径。 2、空间几何体的三视图 定义三视图：正视图（光线从几何体的前面向后面正投影）；侧视图（从左向右）、 俯视图（从上向下） 注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度； 　　俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度； 侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。 3、空间几何体的直观图——斜二测画法 斜二测画法特点：①原来与 x 轴平行的线段仍然与 x 平行且长度不变； ②原来与 y 轴平行的线段仍然与 y 平行，长度为原来的一半。 4、柱体、锥体、台体的表面积与体积 （1）几何体的表面积为几何体各个面的面积的和。 ''''' EDCBAABCDE − 'AD ''''' EDCBAP − ''''' EDCBAP − （2）特殊几何体表面积公式（c 为底面周长，h 为高， 为斜高，l 为母线） （3）柱体、锥体、台体的体积公式 （4）球体的表面积和体积公式：V = ； S = 4、空间点、直线、平面的位置关系 （1）平面 ① 平面的概念： A.描述性说明； B.平面是无限伸展的； ② 平面的表示：通常用希腊字母α、β、γ表示，如平面α（通常写在一个锐角内）； 也可以用两个相对顶点的字母来表示，如平面 BC。 ③ 点与平面的关系：点 A 在平面 内，记作 ；点 不在平面 内，记作 点与直线的关系：点 A 的直线 l 上，记作：A∈l； 点 A 在直线 l 外，记作 A l； 直线与平面的关系：直线 l 在平面α内，记作 l α；直线 l 不在平面α内，记作 l α。 （2）公理 1：如果一条直线的两点在一个平面内，那么这条直线是所有的点都在这个平面内。 （即直线在平面内，或者平面经过直线） 应用：检验桌面是否平； 判断直线是否在平面内 用符号语言表示公理 1： （3）公理 2：经过不在同一条直线上的三点，有且只有一个平面。 推论：一直线和直线外一点确定一平面；两相交直线确定一平面；两平行直线确定一平面。 公理 2 及其推论作用：①它是空间内确定平面的依据 ②它是证明平面重合的依据 （4）公理 3：如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 符号：平面α和β相交，交线是 a，记作α∩β＝a。 符号语言： 公理 3 的作用： ①它是判定两个平面相交的方法。 ②它说明两个平面的交线与两个平面公共点之间的关系：交线必过公共点。 ③它可以判断点在直线上，即证若干个点共线的重要依据。 （5）公理 4：平行于同一条直线的两条直线互相平行 （6）空间直线与直线之间的位置关系 ① 异面直线定义：不同在任何一个平面内的两条直线 'h chS =直棱柱侧面积 rhS π2=圆柱侧 '2 1 chS =正棱锥侧面积 rlS π=圆锥侧面积 ')(2 1 21 hccS +=正棱台侧面积 lRrS π)( +=圆台侧面积 ( )lrrS += π2圆柱表 ( )lrrS += π圆锥表 ( )22 RRlrlrS +++= π圆台表 V Sh=柱 2V Sh r hπ= =圆柱 1 3V Sh=锥 hrV 2 3 1π=圆锥 ' '1 ( )3V S S S S h= + +台 ' ' 2 21 1( ) ( )3 3V S S S S h r rR R hπ= + + = + +圆台 球 34 3 Rπ 球面 24 Rπ α A α∈ A α A α∉ ∉ ⊂ ⊄ , , ,A l B l A B lα α α∈ ∈ ∈ ∈ ⇒ ⊂ ,P A B A B l P l∈ ⇒ = ∈  ② 异面直线性质：既不平行，又不相交。 ③ 异面直线判定：过平面外一点与平面内一点的直线与平面内不过该店的直线是异面直线 ④ 异面直线所成角：直线 a、b 是异面直线，经过空间任意一点 O，分别引直线 a’∥a，b’∥b，则把直线 a’和 b’所成 的锐角（或直角）叫做异面直线 a 和 b 所成的角。两条异面直线所成角的范围是（0°，90°]，若两条异面直线所成 的角是直角，我们就说这两条异面直线互相垂直。 说明：（1）判定空间直线是异面直线方法：①根据异面直线的定义；②异面直线的判定定理 （2）在异面直线所成角定义中，空间一点 O 是任取的，而和点 O 的位置无关。 ②求异面直线所成角步骤： A、利用定义构造角，可固定一条，平移另一条，或两条同时平移到某个特殊的位置，顶点选在特殊的位置上。 B、 证明作出的角即为所求角 C、利用三角形来求角 （7）等角定理：如果一个角的两边和另一个角的两边分别平行，那么这两角相等或互补。 （8）空间直线与平面之间的位置关系 直线在平面内——有无数个公共点． 三种位置关系的符号表示：a α a∩α＝A a∥α （9）平面与平面之间的位置关系：平行——没有公共点；α∥β 相交——有一条公共直线。α∩β＝b 5、空间中的平行问题 （1）直线与平面平行的判定及其性质 线面平行的判定定理：平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。 线线平行 线面平行 线面平行的性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交， 那么这条直线和交线平行。线面平行 线线平行 （2）平面与平面平行的判定及其性质 两个平面平行的判定定理 （1）如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行 （线面平行→面面平行）， （2）如果在两个平面内，各有两组相交直线对应平行，那么这两个平面平行。 （线线平行→面面平行）， （3）垂直于同一条直线的两个平面平行， 两个平面平行的性质定理 （1）如果两个平面平行，那么某一个平面内的直线与另一个平面平行。（面面平行→线面平行） （2）如果两个平行平面都和第三个平面相交，那么它们的交线平行。（面面平行→线线平行） 7、空间中的垂直问题 （1）线线、面面、线面垂直的定义 ①两条异面直线的垂直：如果两条异面直线所成的角是直角，就说这两条异面直线互相垂直。 ②线面垂直：如果一条直线和一个平面内的任何一条直线垂直，就说这条直线和这个平面垂直。 ③平面和平面垂直：如果两个平面相交，所成的二面角（从一条直线出发的两个半平面所组成的图形）是直二面角（平 面角是直角），就说这两个平面垂直。 （2）垂直关系的判定和性质定理 ①线面垂直判定定理和性质定理 判定定理：如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直这个平面。 性质定理：如果两条直线同垂直于一个平面，那么这两条直线平行。 ②面面垂直的判定定理和性质定理 判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。 性质定理：如果两个平面互相垂直，那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。 9、空间角问题 （1）直线与直线所成的角 ①两平行直线所成的角：规定为 。 ⊂ ⇒ ⇒ 0 ②两条相交直线所成的角：两条直线相交其中不大于直角的角，叫这两条直线所成的角。 ③两条异面直线所成的角：过空间任意一点 O，分别作与两条异面直线 a，b 平行的直线 ，形成两条相交直线， 这两条相交直线所成的不大于直角的角叫做两条异面直线所成的角。 （2）直线和平面所成的角 ①平面的平行线与平面所成的角：规定为 。 ②平面的垂线与平面所成的角：规定为 。 ③平面的斜线与平面所成的角：平面的一条斜线和它在平面内的射影所成的锐角，叫做这条直线和这个平面所成的角。 求斜线与平面所成角的思路类似于求异面直线所成角：“一作，二证，三计算”。 在“作角”时依定义关键作射影，由射影定义知关键在于斜线上一点到面的垂线， 在解题时，注意挖掘题设中两个主要信息：（1）斜线上一点到面的垂线；（2）过斜线上的一点或过斜线的平面与已 知面垂直，由面面垂直性质易得垂线。 （3）二面角和二面角的平面角 ①二面角的定义：从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面 叫做二面角的面。 ②二面角的平面角：以二面角的棱上任意一点为顶点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角 叫二面角的平面角。 ③直二面角：平面角是直角的二面角叫直二面角。 两相交平面如果所组成的二面角是直二面角，那么这两个平面垂直；反过来，如果两个平面垂直，那么所成的二面角 为直二面角 ④求二面角的方法 定义法：在棱上选择有关点，过这个点分别在两个面内作垂直于棱的射线得到平面角 垂面法：已知二面角内一点到两个面的垂线时，过两垂线作平面与两个面的交线所成的角为二面角的平面角 7、空间直角坐标系 （1）定义：如图， 是单位正方体.以 A 为原点， 分别以 OD,O ,OB 的方向为正方向，建立三条数轴 。 这时建立了一个空间直角坐标系 Oxyz. 1）O 叫做坐标原点 2）x 轴，y 轴，z 轴叫做坐标轴. 3）过每两个坐标轴的平面叫做坐标面。 （2）右手表示法： 令右手大拇指、食指和中指相互垂直时，可能形成的位置。大拇指指向为 x 轴正方向，食指指向 为 y 轴正向，中指指向则为 z 轴正向，这样也可以决定三轴间的相位置。 （3）任意点坐标表示：空间一点 M 的坐标可以用有序实数组 来表示，有序实数组 叫做点 M 在此空间 直角坐标系中的坐标，记作 （x 叫做点 M 的横坐标，y 叫做点 M 的纵坐标，z 叫做点 M 的竖坐标） （4）空间两点距离坐标公式： 2 12 2 12 2 12 )()()( zzyyxxd −+−+−= ba ′′, 0 90 , , , ,OBCD D A B C− ,A x轴. y轴. z轴 ( , , )x y z ( , , )x y z ( , , )M x y z 高一数学必修 3 公式总结以及例题 §1 算法初步  秦九韶算法：通过一次式的反复计算逐步得出高次多项式的值，对于一个 n 次多项式，只要作 n 次乘法和 n 次加法即可。表达式如下： 例题：秦九韶算法计算多项式 答案： 6 ， 6  理解算法的含义：一般而言，对于一类问题的机械的、统一的求解方法称为算法，其意义具有广泛的含义， 如：广播操图解是广播操的算法，歌谱是一首歌的算法，空调说明书是空调使用的算法… (algorithm) 1. 描述算法有三种方式：自然语言，流程图，程序设计语言（本书指伪代码）. 2. 算法的特征： ①有限性：算法执行的步骤总是有限的，不能无休止的进行下去 ②确定性：算法的每一步操作内容和顺序必须含义确切，而且必须有输出，输出可以是一个或多个。没有输出的算法 是无意义的。 ③可行性：算法的每一步都必须是可执行的，即每一步都可以通过手工或者机器在一定时间内可以完成，在时间上有 一个合理的限度 3. 算法含有两大要素：①操作：算术运算，逻辑运算，函数运算，关系运算等②控制结构:顺序结构，选择结构， 循环结构  流程图：（flow chart）: 是用一些规定的图形、连线及简单的文字说明表示算法及程序结构的一种图形程序， 它直观、清晰、易懂，便于检查及修改。 注意：1. 画流程图的时候一定要清晰，用铅笔和直尺画，要养成有开始和结束的好习惯 2. 拿不准的时候可以先根据结构特点画出大致的流程，反过来再检查，比如：遇到判断框时，往往临界的范围或者条 件不好确定，就先给出一个临界条件，画好大致流程，然后检查这个条件是否正确，再考虑是否取等号的问题，这时 候也就可以有几种书写方法了。 3. 在输出结果时，如果有多个输出，一定要用流程线把所有的输出总结到一起，一起终结到结束框。  算法结构： 顺序结构，选择结构，循环结构 直到型循环 当型循环 ( )( )( )( ) 12211 1 1 ...... axaxxaxaxaaxaxa nnn n n n n +++++=+++ −− − − ,1876543 23456 ++++++ xxxxxx ,0.4 x 时当 = ?运算需要做几次加法和乘法 ( )( )( )( )( ) 1876543x: ++++++ xxxxx即 A B Y N A B p N Y A p Y N N p A Ⅰ.顺序结构（sequence structure ）：是一种最简单最基本的结构它不存在条件判断、控制转移和重复执行的操 作，一个顺序结构的各部分是按照语句出现的先后顺序执行的。 Ⅱ.选择结构（selection structure ）：或者称为分支结构。其中的判断框，书写时主要是注意临界条件的确定。 它有一个入口，两个出口，执行时只能执行一个语句，不能同时执行，其中的 A,B 两语句可以有一个为空，既不执行 任何操作，只是表明在某条件成立时，执行某语句，至于不成立时，不执行该语句，也不执行其它语句。 Ⅲ.循环结构（cycle structure）：它用来解决现实生活中的重复操作问题，分直到型（until）和当型(while)两种 结构(见上图)。当事先不知道是否至少执行一次循环体时（即不知道循环次数时）用当型循环。  基本算法语句：本书中指的是伪代码（pseudo code），且是使用 BASIC 语言编写的,是介于自然 语言和机器语言之间的文字和符号，是表达算法的简单而实用的好方法。伪代码没有统一的格式，只要 书写清楚，易于理解即可，但也要注意符号要相对统一，避免引起混淆。如：赋值语句中可以用 ， 也可以用 ; 表示两变量相乘时可以用“*”，也可以用“ ” Ⅰ. 赋值语句（assignment statement）：用 表示， 如： ，表示将 y 的值赋给 x，其中 x 是一个变量， y 是一个与 x 同类型的变量或者表达式. 一般格式：“ ” ，有时在伪代码的书写时也可以用 “ ”，但此时的 “ = ”不是数学 运算中的等号，而应理解为一个赋值号。 注： 1. 赋值号左边只能是变量，不能是常数或者表达式，右边可以是常数或者表达式。“ = ”具有计算功能。如： 3 = a ,b + 6 = a ,都是错误的，而 a = 3*5 – 1 , a = 2a + 3 都是正确的。2.一个赋值语句一次只能给一个变量赋值。 如：a = b = c = 2 , a , b , c =2 都是错误的，而 a = 3 是正确的. 例题：将 x 和 y 的值交换 , 同样的如果交换三个变量 x,y,z 的值 : Ⅱ. 输入语句（input statement）: Read a ,b 表示输入的数一次送给 a ,b 输出语句（out statement） ：Print x ,y 表示一次输出 运算结果 x ,y 注：1.支持多个输入和输出，但是中间要用逗号隔开！2. Read 语句输入的只能是变量而不是表达式 3. Print 语句不 能起赋值语句，意旨不能在 Print 语句中用 “ = ”4. Print 语句可以输出常量和表达式的值.5.有多个语句在一行 书写时用 “ ； ”隔开. 例题：当 x 等于 5 时，Print “x = ”; x 在屏幕上输出的结果是 x = 5 Ⅲ.条件语句（conditional statement）： 1. 行 If 语句: If A Then B 注：没有 End If 2. 块 If 语句： 注：①不要忘记结束语句 End If ，当有 If 语句嵌套使用时，有几个 If ，就必须要 有几个 End If ②. Else If 是对上一个条件的否定，即已经不属于上面的条件，另外 Else If 后面也要有 End If ③ 注意每个条件的临界性，即某个值是属于上一个条件里，还是属于下一个条件。④ 为了使得书写清晰易懂，应 缩进书写。格式如下： yx = yx ← × ← yx ← 表达式变量 ← yx = py yx xp ← ← ← pz zy yx xp ← ← ← ← 例题: 用条件语句写出求三个数种最大数的一个算法. 或者 注：1. 同样的你可以写出求三个数中最小的数。 2. 也可以类似的求出四个数中最小、大的数 Ⅳ.循环语句（ cycle statement）：  当事先知道循环次数时用 For 循环 ，即使是 N 次也是已知次数的 循环  当循环次数不确定时用 While 循环  Do 循环有两种表达形式，与循环结构的两种循环相对应. 说明：1. While 循环是前测试型的，即满足什么条件才进入循环，其实质是当型循环，一般在解决有关问题时，可 以写成 While 循环，较为简单，因为它的条件相对好判断. 2. 凡是能用 While 循环书写的循环都能用 For 循环书 写 3. While 循环和 Do 循环可以相互转化 4. Do 循环的两种形式也可以相互转化，转化时条件要相应变化 5. 注意 临界条件的判定. 例题： （见课本 ）.99...531 的一个算法设计计算 ×××× 21P If A Then B Else C End If If A Then B Else If C Then D End If Read a , b , c If a≥b Then If a≥c Then Print a Else Print c End If Else If b≥c Then Print b Else Print c End If End If Read a , b , c If a≥b and a≥c Then Print a Else If b≥c Then Print b Else Print c End If For I From 初值 to 终值 Step 步长 … End For For 循环 While A … End While While 循环 Do While p … Loop 当型 Do 循环 Do … Loop Until p 直到型 Do 循环        颜老师友情提醒：1. 一定要看清题意，看题目让你干什么，有的只要写出算法，有的只要求写出伪代码，而有的题目 则是既写出算法画出流程还要写出伪代码。 2. 在具体做题时，可能好多的同学感觉先画流程图较为简单，但也有的算法伪代码比较好写，你也可以在草稿纸上按 照你自己的思路先做出来，然后根据题目要求作答。一般是先写算法，后画流程图，最后写伪代码。 3. 书写程序时一定要规范化，使用统一的符号，最好与教材一致，由于是新教材的原因，再加上各种版本，可能同学 会看到各种参考书上的书写格式不一样，而且有时还会碰到我们没有见过的语言，希望大家能以课本为依据，不要被 铺天盖地的资料所淹没！ SintPr End ISS 2Step99To3FromI 1 For For S ×← ← SintPr hileEnd ISS 2II 97Ihile 1 1 W W I S ×← +← ≤ ← ← SintPr hileEnd 2II ISS 99Ihile 1 1 W W I S +← ×← ≤ ← ← SintPr )99I(001I 2II ISS o 1 1 >≥ +← ×← ← ← 或者UntilLoop D I S SintPr 99I ISS 2II o 1 1 ≥ ×← +← ← ← UntilLoop D I S SintPr 2II ISS )100I(99I Whileo 1 1 Loop D I S +← ×← <≤ ← ← 或者 SintPr ISS 2II )99I(97I Whileo 1 1 Loop D I S ×← +← <≤ ← ← 或者 高中数学必修 4 知识点 2、角 的顶点与原点重合，角的始边与 轴的非负半轴重合，终边落在第几象限，则称 为第几象限 角． 第一象限角的集合为 第二象限角的集合为 第三象限角的集合为 第四象限角的集合为 终边在 轴上的角的集合为 终边在 轴上的角的集合为 终边在坐标轴上的角的集合为 3、与角 终边相同的角的集合为 4、已知 是第几象限角，确定 所在象限的方法：先把各象限均分 等份，再从 轴的正半轴 的上方起，依次将各区域标上一、二、三、四，则 原来是第几象限对应的标号即为 终边所落在的 区域． 5、长度等于半径长的弧所对的圆心角叫做 弧度． 6、半径为 的圆的圆心角 所对弧的长为 ，则角 的弧度数的绝对值是 ． 7、弧度制与角度制的换算公式： ， ， ． 8、若扇形的圆心角为 ，半径为 ，弧长为 ，周长为 ，面积为 ，则 ， ， ． 9 、 设 是 一 个 任 意 大 小 的 角 ， 的 终 边 上 任 意 一 点 的 坐 标 是 ， 它 与 原 点 的 距 离 是 ，则 ， ， ．    正角: 按逆时针方向旋转形成的角 1、任意角 负角: 按顺时针方向旋转形成的角 零角: 不作任何旋转形成的角 α x α { }360 360 90 ,k k kα α⋅ < < ⋅ + ∈Ζ   { }360 90 360 180 ,k k kα ⋅ + < ⋅ + ∈Ζ    { }360 180 360 270 ,k k kα α⋅ + < < ⋅ + ∈Ζ    { }360 270 360 360 ,k k kα α⋅ + < < ⋅ + ∈Ζ    x { }180 ,k kα α = ⋅ ∈Ζ y { }180 90 ,k kα α = ⋅ + ∈Ζ  { }90 ,k kα α = ⋅ ∈Ζ α { }360 ,k kβ β α= ⋅ + ∈Ζ α ( )*nn α ∈Ν n x α n α 1 r α l α l r α = 2 360π =  1 180 π= 1801 57.3π  = ≈     ( )α α为弧度制 r l C S l r α= 2C r l= + 21 1 2 2S lr rα= = α α Ρ ( ),x y ( )2 2 0r r x y= + > sin y r α = cos x r α = ( )tan 0y xx α = ≠ P v x y A O M T 10、三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余 弦为正． 11、三角函数线： ， ， ． 12、同角三角函数的基本关系： ； ． 13、三角函数的诱导公式： ， ， ． ， ， ． ， ， ． ， ， ． 口诀：函数名称不变，符号看象限． ， ． ， ． 口诀：正弦与余弦互换，符号看象限． 14、函数 的图象上所有点向左（右）平移 个单位长度，得到函数 的图象；再将 函数 的图象上所有点的横坐标伸长（缩短）到原来的 倍（纵坐标不变），得到函数 的图象；再将函数 的图象上所有点的纵坐标伸长（缩短）到原来的 倍 （横坐标不变），得到函数 的图象． 函数 的图象上所有点的横坐标伸长（缩短）到原来的 倍（纵坐标不变），得到函数 的图象；再将函数 的图象上所有点向左（右）平移 个单位长度，得到函数 的图象；再将函数 的图象上所有点的纵坐标伸长（缩短）到原来的 倍 （横坐标不变），得到函数 的图象． sinα = ΜΡ cosα = ΟΜ tanα = ΑΤ ( ) 2 21 sin cos 1α α+ = ( )2 2 2 2sin 1 cos ,cos 1 sinα α α α= − = − ( ) sin2 tancos α αα = sinsin tan cos ,cos tan αα α α α α  = =   ( ) ( )1 sin 2 sinkπ α α+ = ( )cos 2 coskπ α α+ = ( ) ( )tan 2 tank kπ α α+ = ∈Ζ ( ) ( )2 sin sinπ α α+ = − ( )cos cosπ α α+ = − ( )tan tanπ α α+ = ( ) ( )3 sin sinα α− = − ( )cos cosα α− = ( )tan tanα α− = − ( ) ( )4 sin sinπ α α− = ( )cos cosπ α α− = − ( )tan tanπ α α− = − ( )5 sin cos2 π α α − =   cos sin2 π α α − =   ( )6 sin cos2 π α α + =   cos sin2 π α α + = −   siny x= ϕ ( )siny x ϕ= + ( )siny x ϕ= + 1 ω ( )siny xω ϕ= + ( )siny xω ϕ= + Α ( )siny xω ϕ= Α + siny x= 1 ω siny xω= siny xω= ϕ ω ( )siny xω ϕ= + ( )siny xω ϕ= + Α ( )siny xω ϕ= Α + 函数 的性质： ①振幅： ；②周期： ；③频率： ；④相位： ；⑤初相： ． 函数 ，当 时，取得最小值为 ；当 时，取得最大值为 ，则 ， ， ． 15、正弦函数、余弦函数和正切函数的图象与性质： 图象 定义域 值域 最值 当 ；当 时， ． 当 时， ；当 时， ． 既无最大值也无最小值 周期性 奇偶性 奇函数 偶函数 奇函数 单调性 在 上是增函数；在 上是减函数． 在 上是增函数 在 上是减函数． 在 上是增函数． 对称性 对称中心 对称轴 对称中心 对称中心 无对称轴 ( )( )sin 0, 0y xω ϕ ω= Α + Α > > Α 2π ωΤ = 1 2f ω π= =Τ xω ϕ+ ϕ ( )siny xω ϕ= Α + + Β 1x x= miny 2x x= maxy ( )max min 1 2 y yΑ = − ( )max min 1 2 y yΒ = + ( )2 1 1 22 x x x x Τ = − < siny x= cosy x= tany x= R R ,2x x k k ππ ≠ + ∈Ζ    [ ]1,1− [ ]1,1− R 2 2x k ππ= + ( )k ∈Ζ max 1y = 2 2x k ππ= − ( )k ∈Ζ min 1y = − ( )2x k kπ= ∈Ζ max 1y = 2x kπ π= + ( )k ∈Ζ min 1y = − 2π 2π π 2 ,22 2k k π ππ π − +   ( )k ∈Ζ 32 ,22 2k k π ππ π + +   ( )k ∈Ζ [ ]( )2 ,2k k kπ π π− ∈Ζ [ ]2 , 2k kπ π π+ ( )k ∈Ζ ,2 2k k π ππ π − +   ( )k ∈Ζ ( )( ),0k kπ ∈Ζ ( ) 2x k k ππ= + ∈Ζ ( ),02k k ππ + ∈Ζ   ( ),02 k k π  ∈Ζ   函 数性 质 对称轴 16、向量：既有大小，又有方向的量． 数量：只有大小，没有方向的量． 有向线段的三要素：起点、方向、长度． 零向量：长度为 的向量． 单位向量：长度等于 个单位的向量． 平行向量（共线向量）：方向相同或相反的非零向量．零向量与任一向量平行． 相等向量：长度相等且方向相同的向量． 17、向量加法运算： ⑴三角形法则的特点：首尾相连． ⑵平行四边形法则的特点：共起点． ⑶三角形不等式： ． ⑷运算性质：①交换律： ；②结合律： ；③ ． ⑸坐标运算：设 ， ，则 ． 18、向量减法运算： ⑴三角形法则的特点：共起点，连终点，方向指向被减向量． ⑵坐标运算：设 ， ，则 ． 设 、 两点的坐标分别为 ， ，则 ． 19、向量数乘运算： ⑴实数 与向量 的积是一个向量的运算叫做向量的数乘，记作 ． ① ； ②当 时， 的方向与 的方向相同；当 时， 的方向与 的方向相反；当 时， ． ⑵运算律：① ；② ；③ ． ⑶坐标运算：设 ，则 ． 20、向量共线定理：向量 与 共线，当且仅当有唯一一个实数 ，使 ． 设 ， ，其中 ，则当且仅当 时，向量 、 共线． 21、平面向量基本定理：如果 、 是同一平面内的两个不共线向量，那么对于这一平面内的任意向量 ，有且只有 ( )x k kπ= ∈Ζ 0 1 a b a b a b− ≤ + ≤ +     a b b a+ = +   ( ) ( )a b c a b c+ + = + +     0 0a a a+ = + =    ( )1 1,a x y= ( )2 2,b x y= ( )1 2 1 2,a b x x y y+ = + + ( )1 1,a x y= ( )2 2,b x y= ( )1 2 1 2,a b x x y y− = − − Α Β ( )1 1,x y ( )2 2,x y ( )1 2 1 2,x x y yΑΒ = − − λ a aλ  a aλ λ=  0λ > aλ  a 0λ < aλ  a 0λ = 0aλ =  ( ) ( )a aλ µ λµ=  ( )a a aλ µ λ µ+ = +   ( )a b a bλ λ λ+ = +   ( ),a x y= ( ) ( ), ,a x y x yλ λ λ λ= = ( )0a a ≠   b λ b aλ=  ( )1 1,a x y= ( )2 2,b x y= 0b ≠  1 2 2 1 0x y x y− = a ( )0b b ≠   1e 2e a b a C Β Α a b C C− = Α − ΑΒ = Β   一对实数 、 ，使 ．（不共线的向量 、 作为这一平面内所有向量的一组基底） 22、分点坐标公式：设点 是线段 上的一点， 、 的坐标分别是 ， ，当 时，点 的坐标是 ． 23、平面向量的数量积： ⑴ ．零向量与任一向量的数量积为 ． ⑵性质：设 和 都是非零向量，则① ．②当 与 同向时， ；当 与 反向时， ； 或 ．③ ． ⑶运算律：① ；② ；③ ． ⑷坐标运算：设两个非零向量 ， ，则 ． 若 ，则 ，或 ． 设 ， ，则 ． 设 、 都是非零向量， ， ， 是 与 的夹角，则 ． 24、两角和与差的正弦、余弦和正切公式： ⑴ ； ⑵ ； ⑶ ； ⑷ ； ⑸ （ ）； ⑹ （ ）． 25、二倍角的正弦、余弦和正切公式： ⑴ ． ⑵ （ ， ）． 1 λ 2 λ 1 1 2 2a e eλ λ= +  1e 2e Ρ 1 2 Ρ Ρ 1 Ρ 2 Ρ ( )1 1,x y ( )2 2,x y 1 2 λΡ Ρ = ΡΡ  Ρ 1 2 1 2,1 1 x x y yλ λ λ λ + +   + +  ( )cos 0, 0,0 180a b a b a bθ θ⋅ = ≠ ≠ ≤ ≤       0 a b 0a b a b⊥ ⇔ ⋅ =   a b a b a b⋅ =   a b a b a b⋅ = −   22a a a a⋅ = =    a a a= ⋅   a b a b⋅ ≤   a b b a⋅ = ⋅   ( ) ( ) ( )a b a b a bλ λ λ⋅ = ⋅ = ⋅     ( )a b c a c b c+ ⋅ = ⋅ + ⋅      ( )1 1,a x y= ( )2 2,b x y= 1 2 1 2a b x x y y⋅ = + ( ),a x y= 2 2 2a x y= + 2 2a x y= + ( )1 1,a x y= ( )2 2,b x y= 1 2 1 2 0a b x x y y⊥ ⇔ + = a b ( )1 1,a x y= ( )2 2,b x y= θ a b 1 2 1 2 2 2 2 2 1 1 2 2 cos x x y ya b a b x y x y θ +⋅= = + +   ( )cos cos cos sin sinα β α β α β− = + ( )cos cos cos sin sinα β α β α β+ = − ( )sin sin cos cos sinα β α β α β− = − ( )sin sin cos cos sinα β α β α β+ = + ( ) tan tantan 1 tan tan α βα β α β −− = + ( )( )tan tan tan 1 tan tanα β α β α β− = − + ( ) tan tantan 1 tan tan α βα β α β ++ = − ( )( )tan tan tan 1 tan tanα β α β α β+ = + − sin 2 2sin cosα α α= 2 2 2 2cos2 cos sin 2cos 1 1 2sinα α α α α= − = − = − 2 cos2 1cos 2 αα += 2 1 cos2sin 2 αα −= ⑶ ． 26、 ，其中 ． 高中数学必修 5 知识点 1、正弦定理：在 中， 、 、 分别为角 、 、 的对边， 为 的外接圆的半径，则有 ． 2、正弦定理的变形公式：① ， ， ； ② ， ， ； ③ ； ④ ． 3、三角形面积公式： ． 4、余弦定理：在 中，有 ， ， ． 5、余弦定理的推论： ， ， ． 6、设 、 、 是 的角 、 、 的对边，则：①若 ，则 ； ②若 ，则 ；③若 ，则 ． 7、数列：按照一定顺序排列着的一列数． 8、数列的项：数列中的每一个数． 9、有穷数列：项数有限的数列． 10、无穷数列：项数无限的数列． 11、递增数列：从第 2 项起，每一项都不小于它的前一项的数列． 12、递减数列：从第 2 项起，每一项都不大于它的前一项的数列． 13、常数列：各项相等的数列． 14、摆动数列：从第 2 项起，有些项大于它的前一项，有些项小于它的前一项的数列． 15、数列的通项公式：表示数列 的第 项与序号 之间的关系的公式． 2 2tantan 2 1 tan αα α= − ( )2 2sin cos sinα α α ϕΑ + Β = Α + Β + tanϕ Β= Α C∆ΑΒ a b c Α Β C R C∆ΑΒ 2sin sin sin a b c RC = = =Α Β 2 sina R= Α 2 sinb R= Β 2 sinc R C= sin 2 a R Α = sin 2 b R Β = sin 2 cC R = : : sin :sin :sina b c C= Α Β sin sin sin sin sin sin a b c a b c C C + + = = =Α + Β + Α Β 1 1 1sin sin sin2 2 2CS bc ab C ac∆ΑΒ = Α = = Β C∆ΑΒ 2 2 2 2 cosa b c bc= + − Α 2 2 2 2 cosb a c ac= + − Β 2 2 2 2 cosc a b ab C= + − 2 2 2 cos 2 b c a bc + −Α = 2 2 2 cos 2 a c b ac + −Β = 2 2 2 cos 2 a b cC ab + −= a b c C∆ΑΒ Α Β C 2 2 2a b c+ = 90C =  2 2 2a b c+ > 90C <  2 2 2a b c+ < 90C >  { }na n n 16、数列的递推公式：表示任一项 与它的前一项 （或前几项）间的关系的公式． 17、如果一个数列从第 2 项起，每一项与它的前一项的差等于同一个常数，则这个数列称为等差数列，这个常数称为 等差数列的公差． 18、由三个数 ， ， 组成的等差数列可以看成最简单的等差数列，则 称为 与 的等差中项．若 ， 则称 为 与 的等差中项． 19、若等差数列 的首项是 ，公差是 ，则 ． 20、通项公式的变形：① ；② ；③ ； ④ ；⑤ ． 21、若 是等差数列，且 （ 、 、 、 ），则 ；若 是等差数列，且 （ 、 、 ），则 ． 22、等差数列的前 项和的公式：① ；② ． 23 、 等 差 数 列 的 前 项 和 的 性 质 ： ① 若 项 数 为 ， 则 ， 且 ， ． ② 若 项 数 为 ， 则 ， 且 ， （ 其 中 ， ）． 24、如果一个数列从第 项起，每一项与它的前一项的比等于同一个常数，则这个数列称为等比数列，这个常数称为 等比数列的公比． 25、在 与 中间插入一个数 ，使 ， ， 成等比数列，则 称为 与 的等比中项．若 ，则称 为 与 的等比中项． 26、若等比数列 的首项是 ，公比是 ，则 ． 27、通项公式的变形：① ；② ；③ ；④ ． na 1na − a Α b Α a b 2 a cb += b a c { }na 1a d ( )1 1na a n d= + − ( )n ma a n m d= + − ( )1 1na a n d= − − 1 1 na ad n −= − 1 1na an d −= + n ma ad n m −= − { }na m n p q+ = + m n p *q∈Ν m n p qa a a a+ = + { }na 2n p q= + n p *q∈Ν 2 n p qa a a= + n ( )1 2 n n n a aS += ( ) 1 1 2n n nS na d −= + n ( )*2n n∈Ν ( )2 1n n nS n a a += + S S nd− =偶 奇 1 n n S a S a + =奇 偶 ( )*2 1n n− ∈Ν ( )2 1 2 1n nS n a− = − nS S a− =奇 偶 1 S n S n = − 奇 偶 nS na=奇 ( )1 nS n a= −偶 2 a b G a G b G a b 2G ab= G a b { }na 1a q 1 1 n na a q −= n m n ma a q −= ( )1 1 n na a q − −= 1 1 n naq a − = n m n m aq a − = 28、若 是等比数列，且 （ 、 、 、 ），则 ；若 是等比数列，且 （ 、 、 ），则 ． 29、等比数列 的前 项和的公式： ． 30、等比数列的前 项和的性质：①若项数为 ，则 ． ② ． ③ ， ， 成等比数列． 31、 ； ； ． 32、不等式的性质： ① ；② ；③ ； ④ ， ；⑤ ； ⑥ ；⑦ ； ⑧ ． 33、一元二次不等式：只含有一个未知数，并且未知数的最高次数是 的不等式． 34、二次函数的图象、一元二次方程的根、一元二次不等式的解集间的关系： 判别式 二次函数 的 图 象 一元二次方程 的根 有 两个相异实数根 有两个相等实数根 没有实数根 一元二次 不等式的解集 { }na m n p q+ = + m n p *q∈Ν m n p qa a a a⋅ = ⋅ { }na 2n p q= + n p *q∈Ν 2 n p qa a a= ⋅ { }na n ( ) ( ) ( ) 1 1 1 1 1 11 1 n n n na q S a q a a q qq q = = − −= ≠ − − n ( )*2n n∈Ν S qS =偶 奇 n n m n mS S q S+ = + ⋅ nS 2n nS S− 3 2n nS S− 0a b a b− > ⇔ > 0a b a b− = ⇔ = 0a b a b− < ⇔ < a b b a> ⇔ < ,a b b c a c> > ⇒ > a b a c b c> ⇒ + > + , 0a b c ac bc> > ⇒ > , 0a b c ac bc> < ⇒ < ,a b c d a c b d> > ⇒ + > + 0, 0a b c d ac bd> > > > ⇒ > ( )0 , 1n na b a b n n> > ⇒ > ∈Ν > ( )0 , 1n na b a b n n> > ⇒ > ∈Ν > 2 2 4b ac∆ = − 0∆ > 0∆ = 0∆ < 2y ax bx c= + + ( )0a > 2 0ax bx c+ + = ( )0a > 1,2 2 bx a − ± ∆= ( )1 2x x< 1 2 2 bx x a = = − 2 0ax bx c+ + > { }1 2x x x x x< >或 2 bx x a  ≠ −    R 35、二元一次不等式：含有两个未知数，并且未知数的次数是 的不等式． 36、二元一次不等式组：由几个二元一次不等式组成的不等式组． 37、二元一次不等式（组）的解集：满足二元一次不等式组的 和 的取值构成有序数对 ，所有这样的有序数 对 构成的集合． 38、在平面直角坐标系中，已知直线 ，坐标平面内的点 ． ①若 ， ，则点 在直线 的上方． ②若 ， ，则点 在直线 的下方． 39、在平面直角坐标系中，已知直线 ． ①若 ，则 表示直线 上方的区域； 表示直线 下方的区域． ②若 ，则 表示直线 下方的区域； 表示直线 上方的区域． 40、线性约束条件：由 ， 的不等式（或方程）组成的不等式组，是 ， 的线性约束条件． 目标函数：欲达到最大值或最小值所涉及的变量 ， 的解析式． 线性目标函数：目标函数为 ， 的一次解析式． 线性规划问题：求线性目标函数在线性约束条件下的最大值或最小值问题． 可行解：满足线性约束条件的解 ． 可行域：所有可行解组成的集合． 最优解：使目标函数取得最大值或最小值的可行解． 41、设 、 是两个正数，则 称为正数 、 的算术平均数， 称为正数 、 的几何平均数． 42、均值不等式定理： 若 ， ，则 ，即 ． ( )0a > 2 0ax bx c+ + < ( )0a > { }1 2x x x x< < ∅ ∅ 1 x y ( ),x y ( ),x y 0x y CΑ + Β + = ( )0 0,x yΡ 0Β > 0 0 0x y CΑ + Β + > ( )0 0,x yΡ 0x y CΑ + Β + = 0Β > 0 0 0x y CΑ + Β + < ( )0 0,x yΡ 0x y CΑ + Β + = 0x y CΑ + Β + = 0Β > 0x y CΑ + Β + > 0x y CΑ + Β + = 0x y CΑ + Β + < 0x y CΑ + Β + = 0Β < 0x y CΑ + Β + > 0x y CΑ + Β + = 0x y CΑ + Β + < 0x y CΑ + Β + = x y x y x y x y ( ),x y a b 2 a b+ a b ab a b 0a > 0b > 2a b ab+ ≥ 2 a b ab + ≥ 43、常用的基本不等式：① ；② ； ③ ；④ ． 44、极值定理：设 、 都为正数，则有 ⑴若 （和为定值），则当 时，积 取得最大值 ． ⑵若 （积为定值），则当 时，和 取得最小值 ． ( )2 2 2 ,a b ab a b R+ ≥ ∈ ( )2 2 ,2 a bab a b R +≤ ∈ ( )2 0, 02 a bab a b + ≤ > >   ( )22 2 ,2 2 a b a b a b R + + ≥ ∈   x y x y s+ = x y= xy 2 4 s xy p= x y= x y+ 2 p