高考圆锥曲线之弦长为定值问题

高考圆锥曲线之弦长为定值问题

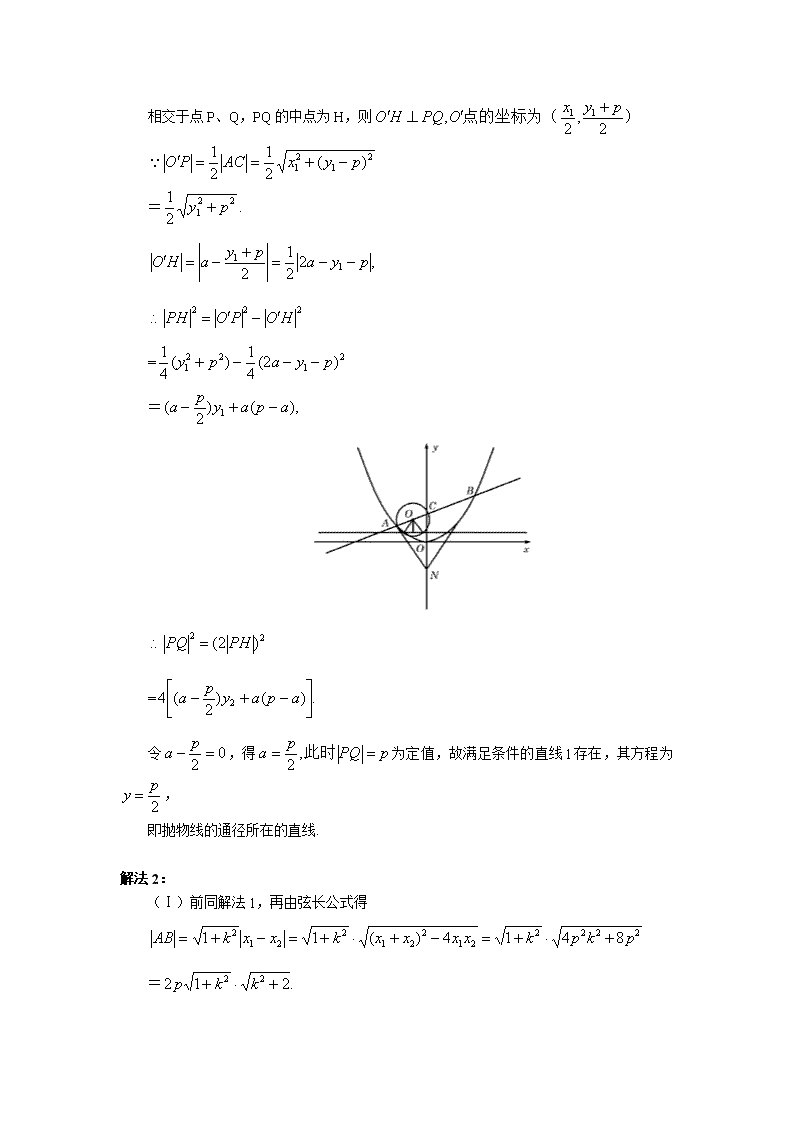
题型七：弦或弦长为定值问题 例题9、（07湖北理科）在平面直角坐标系xOy中，过定点C（0，p）作直线与抛物线x2=2py（p>0）相交于A、B两点。‎ ‎（Ⅰ）若点N是点C关于坐标原点O的对称点，求△ANB面积的最小值；‎ ‎（Ⅱ）是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得弦长恒为定值？若存在，求出l的方程；若不存在，说明理由。（此题不要求在答题卡上画图）‎ 本小题主要考查直线、圆和抛物线等平面解析几何的基础知识，考查综合运用数学知识进行推理运算的能力和解决问题的能力.‎ 解法1：‎ ‎（Ⅰ）依题意，点N的坐标为N（0,-p）,可设A（x1,y1）,B（x2,y2），直线AB的方程为y=kx+p,与x2=2py联立得消去y得x2-2pkx-2p2=0.‎ 由韦达定理得x1+x2=2pk,x1x2=-2p2.‎ 于是 ‎＝‎ ‎＝‎ ‎.‎ ‎（Ⅱ）假设满足条件的直线l存在，其方程为y=a,AC的中点为 径的圆相交于点P、Q，PQ的中点为H，则 ‎＝.‎ ‎=‎ ‎＝‎ ‎=‎ 令，得为定值，故满足条件的直线l存在，其方程为，‎ 即抛物线的通径所在的直线.‎ 解法2：‎ ‎（Ⅰ）前同解法1，再由弦长公式得 ‎＝‎ 又由点到直线的距离公式得.‎ 从而，‎ ‎（Ⅱ）假设满足条件的直线t存在，其方程为y=a，则以AC为直径的圆的方程为 将直线方程y=a代入得 设直线l与以AC为直径的圆的交点为P（x2,y2）,Q（x4,y4）,则有 令为定值，故满足条件的直线l存在，其方程为.‎ 即抛物线的通径所在的直线。‎ 练习、（山东09理）（22）（本小题满分14分）‎ 设椭圆E: （a,b>0）过M（2，） ，N(,1)两点，O为坐标原点，‎ ‎（I）求椭圆E的方程；‎ ‎（II）是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。‎ 解:（1）因为椭圆E: （a,b>0）过M（2，） ，N(,1)两点,‎ 所以解得所以椭圆E的方程为 ‎（2）假设存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且,设该圆的切线方程为解方程组得,即,‎ 则△=,即 ‎,要使,需使,即,所以,所以又,所以,所以,即或,因为直线为圆心在原点的圆的一条切线,所以圆的半径为,,,所求的圆为,此时圆的切线都满足或,而当切线的斜率不存在时切线为与椭圆的两个交点为或满足,综上, 存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且.‎ 因为,‎ 所以,‎ ‎, ‎ ‎①当时 因为所以,‎ 所以,‎ 所以当且仅当时取”=”.‎ ② 当时,.‎ ③ 当AB的斜率不存在时, 两个交点为或,所以此时,‎ 综上, |AB |的取值范围为即: ‎ ‎【命题立意】:本题属于探究是否存在的问题,主要考查了椭圆的标准方程的确定,直线与椭圆的位置关系直线与圆的位置关系和待定系数法求方程的方法,能够运用解方程组法研究有关参数问题以及方程的根与系数关系.‎ 题型八：角度问题 ‎　例题9、（08重庆理）如图（21）图，M（-2，0）和N（2，0）是平面上的两点，动点P满足：‎ ‎（Ⅰ）求点P的轨迹方程；‎ ‎（Ⅱ）若,求点P的坐标.‎ 解：(Ⅰ)由椭圆的定义，点P的轨迹是以M、N为焦点，长轴长‎2a=6的椭圆.‎ ‎ 因此半焦距c=2，长半轴a=3，从而短半轴 b=，‎ ‎ 所以椭圆的方程为 ‎ (Ⅱ)由得 ‎ ①‎ ‎ 因为不为椭圆长轴顶点，故P、M、N构成三角形.在△PMN中，‎ ‎ ②‎ ‎ 将①代入②，得 ‎ ‎ ‎ 故点P在以M、N为焦点，实轴长为的双曲线上.‎ ‎ 由(Ⅰ)知，点P的坐标又满足，所以 ‎ 由方程组 解得 ‎ 即P点坐标为 练习1、（05福建理）已知方向向量为v=(1,)的直线l过点（0，－2）和椭圆C：(a>b>0)的焦点，且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）是否存在过点E（－2，0）的直线m交椭圆C于点M、N，满足 cot∠MON≠0（O为原点）.若存在，求直线m的方程；若不存在，请说明理由.‎ 本小题主要考查直线、椭圆及平面向量的基本知识，平面解析几何的基本方法和综合解题能力.满分14分.‎ ‎（I）解法一：直线， ① ‎ 过原点垂直的直线方程为， ②‎ 解①②得 ‎∵椭圆中心O（0，0）关于直线的对称点在椭圆C的右准线上，‎ ‎∵直线过椭圆焦点，∴该焦点坐标为（2，0）.‎ ‎ 故椭圆C的方程为 ③‎ 解法二：直线.‎ 设原点关于直线对称点为（p，q），则解得p=3.‎ ‎∵椭圆中心O（0，0）关于直线的对称点在椭圆C的右准线上，‎ ‎ ∵直线过椭圆焦点，∴该焦点坐标为（2，0）.‎ ‎ 故椭圆C的方程为 ③‎ ‎（II）解法一：设M（），N（）.‎ 当直线m不垂直轴时，直线代入③，整理得 ‎ ‎ 点O到直线MN的距离 ‎ 即 ‎ ‎ ‎ ‎ 即 ‎ 整理得 ‎ 当直线m垂直x轴时，也满足.‎ ‎ 故直线m的方程为 ‎ 或或 ‎ 经检验上述直线均满足.‎ 所以所求直线方程为或或 解法二：设M（），N（）.‎ ‎ 当直线m不垂直轴时，直线m：y=k(x+2)代入③，整理得 ‎ ‎ ‎ ∵E（－2，0）是椭圆C的左焦点，‎ ‎ ∴|MN|=|ME|+|NE|‎ ‎=‎ ‎ 以下与解法一相同.‎ 解法三：设M（），N（）.‎ ‎ 设直线，代入③，整理得 ‎ ‎ ‎ |y1-y2|==‎ ‎ 即 ‎ ‎ ‎ ‎ ‎ ‎ ∴=，整理得 ‎ ‎ 解得或 ‎ 故直线m的方程为或或 ‎ 经检验上述直线方程为 ‎ 所以所求直线方程为或或 练习2、（07四川理）设、分别是椭圆的左、右焦点。‎ ‎（Ⅰ）若是该椭圆上的一个动点，求·的最大值和最小值；‎ ‎（Ⅱ）设过定点的直线与椭圆交于不同的两点、，且∠为锐角（其中为坐标原点），求直线的斜率的取值范围。‎ 本题主要考察直线、椭圆、平面向量的数量积等基础知识，以及综合应用数学知识解决问题及推理计算能力。‎ 解：（Ⅰ）解法一：易知 所以，设，则 因为，故当，即点为椭圆短轴端点时，有最小值 当，即点为椭圆长轴端点时，有最大值 解法二：易知，所以，设，则 ‎（以下同解法一）‎ ‎（Ⅱ）显然直线不满足题设条件，可设直线，‎ 联立，消去，整理得：‎ ‎∴‎ 由得：或 又 ‎∴‎ 又 ‎∵，即 ∴‎ 故由①、②得或 练习3、（08陕西理）已知抛物线：，直线交于两点，是线段的中点，过作轴的垂线交于点．‎ ‎（Ⅰ）证明：抛物线在点处的切线与平行；‎ ‎（Ⅱ）是否存在实数使，若存在，求的值；若不存在，说明理由．‎ 解法一：（Ⅰ）如图，设，，把代入得，‎ x A y ‎1‎ ‎1‎ ‎2‎ M N B O 由韦达定理得，，‎ ‎，点的坐标为．‎ 设抛物线在点处的切线的方程为，‎ 将代入上式得，‎ 直线与抛物线相切，‎ ‎，．‎ 即．‎ ‎（Ⅱ）假设存在实数，使，则，又是的中点，‎ ‎．‎ 由（Ⅰ）知 ‎．‎ 轴，．‎ 又 ‎ ．‎ ‎，解得．‎ 即存在，使．‎ 解法二：（Ⅰ）如图，设，把代入得 ‎．由韦达定理得．‎ ‎，点的坐标为．，，‎ 抛物线在点处的切线的斜率为，．‎ ‎（Ⅱ）假设存在实数，使．‎ 由（Ⅰ）知，则 ‎，‎ ‎，，解得．‎ 即存在，使．‎