哈尔滨市第三中学第二次高考模拟考试文科数学试题及答案

哈尔滨市第三中学第二次高考模拟考试文科数学试题及答案

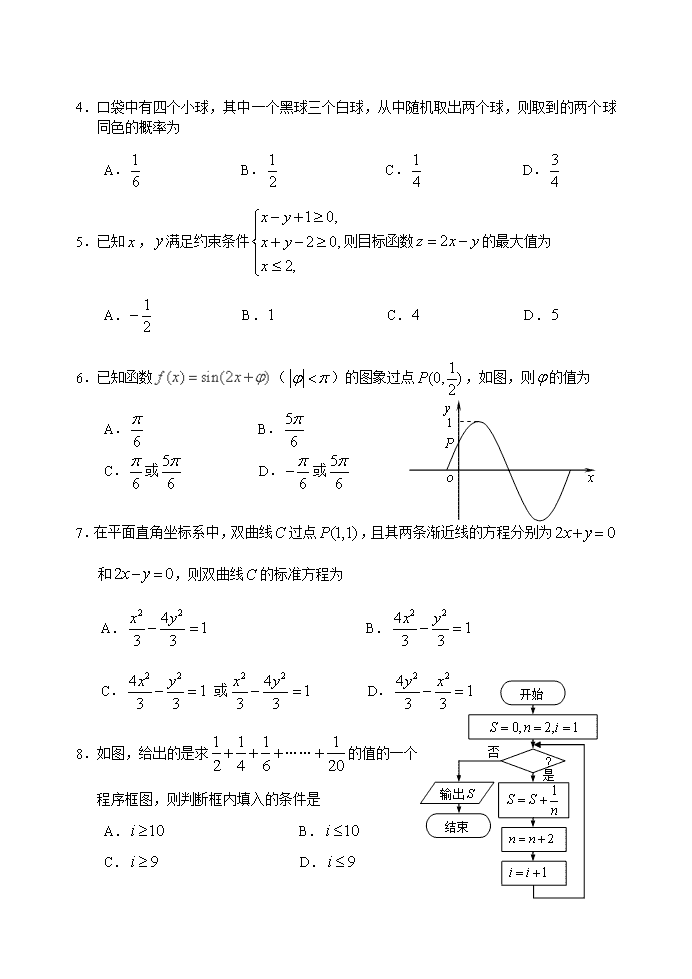
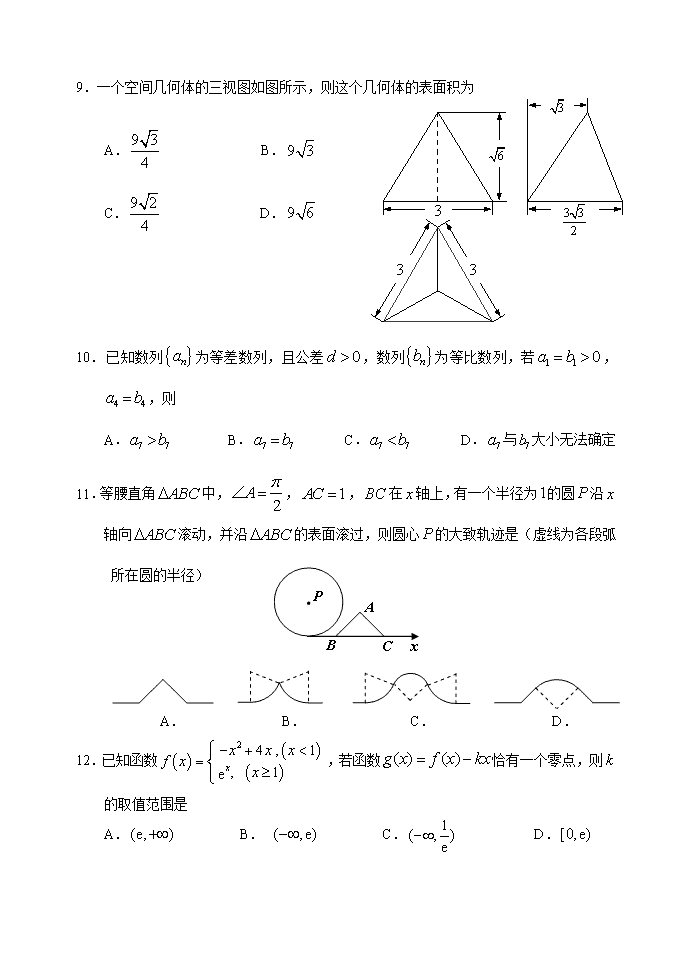
‎2016年哈尔滨市第三中学第二次高考模拟考试 数学试卷（文史类）‎ 考试说明：本试卷分第I卷（选择题）和第II卷（非选择题）两部分，满分150分，考试时间120分钟．‎ ‎（1）答题前，考生先将自己的姓名、准考证号码填写清楚；‎ ‎ （2）选择题必须使用2B铅笔填涂，非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整，字迹清楚；‎ ‎ （3）请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿纸、试题卷上答题无效；‎ ‎ （4）保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀．‎ ‎ 第 I卷 （选择题, 共60分）‎ 一、选择题(共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．)‎ ‎1．设集合，，则 A． B． C． D． ‎ ‎2． 设命题：若，，则；命题：若函数 ，则对任意都有成立．在命题①； ②； ③； ④中，真命题是 A．①③ B． ①④ C． ②③ D． ②④‎ ‎3．已知复数，则 A． B． C． D．‎ ‎4．口袋中有四个小球，其中一个黑球三个白球，从中随机取出两个球，则取到的两个球同色的概率为 A． B． C． D．‎ ‎5．已知，满足约束条件则目标函数的最大值为 A． B． C． D．‎ P ‎6．已知函数（）的图象过点，如图，则的值为 A． B． ‎ ‎ C．或 D．或 ‎ ‎7．在平面直角坐标系中，双曲线过点，且其两条渐近线的方程分别为和，则双曲线的标准方程为 A． B． ‎ ‎?‎ C． 或 D．‎ ‎8．如图，给出的是求……的值的一个 ‎ 程序框图，则判断框内填入的条件是 A． B． ‎ C． D．‎ ‎3‎ ‎9．一个空间几何体的三视图如图所示，则这个几何体的表面积为 A． ‎ B． ‎ ‎ C． D．‎ ‎3‎ ‎3‎ ‎10． 已知数列为等差数列，且公差，数列为等比数列，若，，则 A． B． C． D．与大小无法确定 ‎11．等腰直角中，，，在轴上，有一个半径为的圆沿轴向滚动，并沿的表面滚过，则圆心的大致轨迹是（虚线为各段弧 ‎ 所在圆的半径）‎ ‎ ‎ A． B． C． D．‎ ‎12．已知函数，若函数恰有一个零点，则的取值范围是 A． B． C． D．‎ ‎2016哈尔滨市第三中学第二次高考模拟考试 数学试卷（文史类）‎ 第Ⅱ卷 （非选择题, 共90分）‎ 二、填空题（共4小题，每小题5分，共20分，将答案填在答题卡相应的位置上．）‎ ‎13．已知圆，则过点的圆的切线方程为 ．‎ ‎14．数列中，，当时，，则数列的通项公式为 ．‎ ‎15．点在的边所在直线上，且满足（），则在平面直角坐标系中，动点的轨迹的普通方程为 ．‎ ‎16．四棱锥的底面是边长为的正方形，高为1，其外接球半径为，则正方形的中心与点之间的距离为 ．‎ ‎ ‎ 三、解答题（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．）‎ ‎17．（本小题满分12分） ‎ 已知 ‎（Ⅰ）若，求的值域；‎ ‎（Ⅱ）在中，为边所对的内角若，，求的最大值．‎ ‎18．（本小题满分12分）‎ 某汽车公司为了考查某4S店的服务态度，对到店维修保养的客户进行回访调查，每个用户在到此店维修或保养后可以对该店进行打分，最高分为10分．上个月公司对该4S店的100位到店维修保养的客户进行了调查，将打分的客户按所打分值分成以下几组：第一组[0,2)，第二组[2,4)，第三组[4,6)，第四组[6,8)，第五组[8,10]，得到频率分布直方图如图所示．‎ ‎ （Ⅰ）分别求第四、五组的频率；‎ ‎ （Ⅱ）该公司在第二、三组客户中按分层抽样的方法抽取6名客户进行深入调查，之 后将从这6人中随机抽取2人进行物质奖励，求得到奖励的人来自不同组的概率．‎ ‎19．（本小题满分12分）‎ 棱长为1的正方体中，沿平面将正方体分成两部分，其中一部分如图所示，过直线的平面与线段交于点．‎ ‎ （Ⅰ）当与重合时，求证：；‎ ‎ （Ⅱ）当平面平面时，求平面分几何体所得两部分体积之比．‎ ‎20．（本小题满分12分）‎ 已知抛物线，过其焦点作斜率为1的直线交抛物线C于M、N两点，且．‎ ‎ （Ⅰ）求抛物线C的方程；‎ ‎ （Ⅱ）已知动圆P的圆心在抛物线C上，且过定点D(0，4)，若动圆P与x轴交于A、B两点，且，求的最小值．‎ ‎21．（本小题满分12分）‎ 已知函数，函数 ，其中为大于零的常数．‎ ‎（Ⅰ）求函数的单调区间；‎ ‎（Ⅱ）求证：．‎ ‎22．（本小题满分10分）选修4-1：几何证明选讲 A B C D P Q 等腰梯形中，∥，、交于点，平分，为梯形外接圆的切线，交的延长线于点．‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）若，，，求的长．‎ ‎23．（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系中，曲线的参数方程为 (为参数)， 在以为极点，轴的正半轴为极轴的极坐标系中，曲线的方程为．‎ ‎（Ⅰ）求曲线、的直角坐标方程；‎ ‎（Ⅱ）若、分别为曲线、上的任意点，求的最小值．‎ ‎24．（本小题满分10分）选修4-5：不等式选讲 设函数．‎ ‎（Ⅰ）求不等式的解集；‎ ‎（Ⅱ）若，不等式恒成立，求实数a的取值范围．‎ ‎2016年哈尔滨市第三中学第二次高考模拟考试 ‎ 数学试卷（文史类）答案 一、选择题 DDAB CABB BCDB 二、填空题 ‎13． 14． 15． 16．‎ ‎17．（Ⅰ）， -------------3分 ‎，的值域为；-------------6分 ‎（Ⅱ），，，‎ ‎ -------------9分 ‎，‎ ‎．‎ 的最大值为． -------------12分 ‎18．解：(1)由直方图知，第四组的频率为，第五组的频率为所以第四、五组的频率分别为和． ………………………4分 ‎ (2) 由直方图知，第二、三组客户人数分别为10人和20人，所以抽出的6人中，第二组有2人，设为A，B，第三组有4人，设为a,b,c,d．‎ ‎ 从中随机抽取2人的所有情况如下：‎ ‎ AB，Aa，Ab，Ac，Ad，Ba，Bb，Bc，Bd，ab，ac，ad，bc，bd，cd共15种．…8分 ‎ 其中，两人来自不同组的情况共有8种， ………………………10分 ‎ 所以，得到奖励的人来自不同组的概率为． ………………………12分 ‎19．（Ⅰ）连接，在正方形中，，‎ 正方体中，平面，‎ 平面，，平面，‎ ‎，即；-------------4分 ‎（Ⅱ）当为中点时，‎ A1A1‎ AA M（M）‎ B1B1‎ C1C1‎ CC BB N P 取、中点分别为、，链接、、，‎ ‎，且，‎ 四边形为平行四边形，，‎ 平面平面，，‎ 平面，平面，‎ 平面平面．-------------8分 设，，‎ ‎，‎ ‎．-------------12分 ‎20． 解：(1) 设抛物线的焦点为，则直线，‎ ‎ 由，得 ………………………2分 ‎ ，，‎ ‎ ， ………………………4分 ‎ 抛物线的方程为 ………………………5分 ‎ (2) 设动圆圆心，则，‎ ‎ 且圆，‎ ‎ 令，整理得：，‎ ‎ 解得：， ………………………7分 ‎ ，…………9分 ‎ 当时，，‎ ‎ 当时，，，，‎ ‎ ，‎ ‎ 所以的最小值为． ………………………12分 ‎21．（1）解：，----------------------------------------------------------------1分 令得，则在上单调递增；‎ 令得，则在上单调递减。---------------------3分 ‎（2）.令，---------4分 则，‎ 令，‎ 则，故在上单调递增。-------------------------6分 而，，故存在，使得，‎ 即。---------------------------------------------------------------------------8分 则时，，故；时，，故。‎ 则在上单调递减，在上单调递增，------------------------------------10分 故 ‎。‎ 故。--------------------------------------------------------------12分 ‎22． (1) 为圆的切线，平分 为圆的切线．-------------6分 ‎(2) ，‎ ‎．-------------12分 ‎23．(1) ．-------------6分 ‎(2)设，则，‎ 当且仅当时．-------------12分 ‎24．(1) 或．-------------6分 ‎(2)当时， ，原式恒成立； ‎ 当时，原式等价转换为恒成立，即．‎ ‎，当且仅当即时取等， ．-------------12分