三视图高考类型题老师专用汇总

三视图高考类型题老师专用汇总

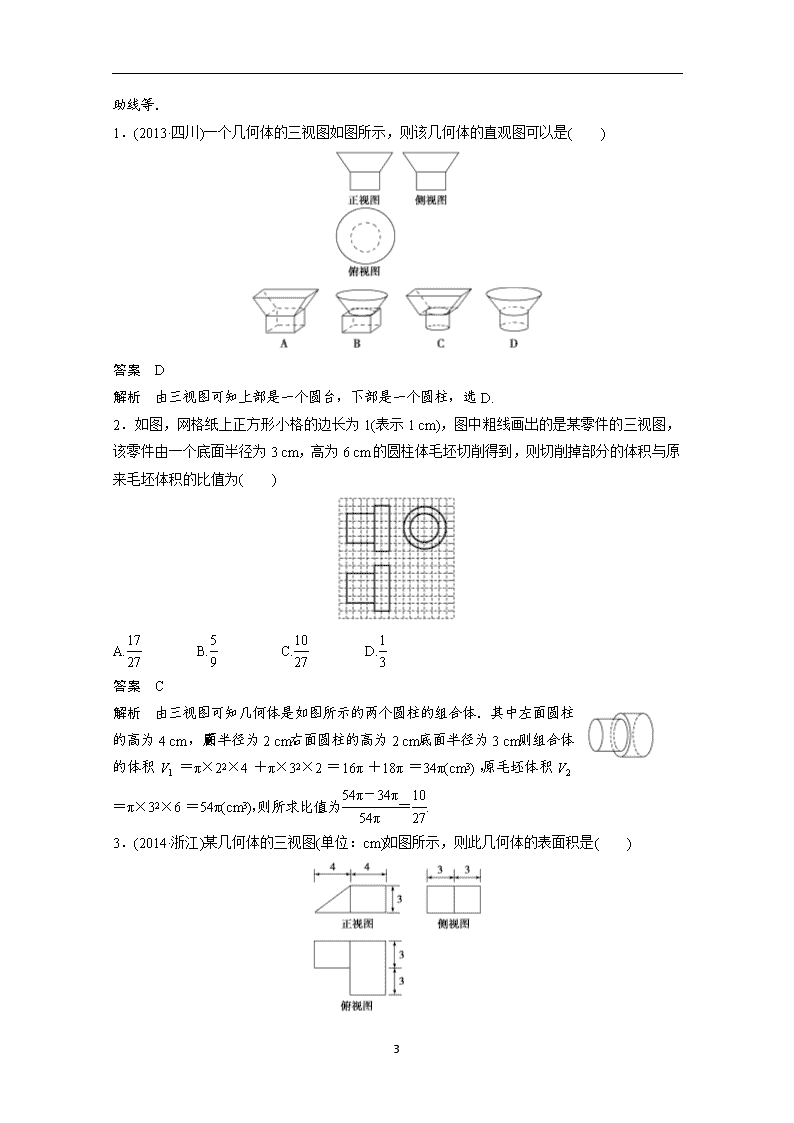
1 三视图类型题 题型一　三视图识图 例 1　将正方体(如图(1)所示)截去两个三棱锥，得到如图(2)所示的几何体，则该几何体的侧(左) 视图为(　　) 破题切入点　根据三视图先确定原几何体的直观图和形状，然后再解题． 答案　B 解析　还原正方体后，将 D1，D，A 三点分别向正方体右侧面作垂线．D1A 的射影为 C1B，且 为实线，B1C 被遮挡应为虚线． 题型二　空间几何体的表面积和体积 例 2　如图是某简单组合体的三视图，则该组合体的体积为(　　) A．36 3(π＋ 2) B．36 3(π＋2) C．108 3π D．108( 3π＋2) 破题切入点　先根据三视图的结构特征确定几何体的构成——半圆锥与棱锥的组合体，然后 把三视图中的数据转化为该组合体的数字特征，分别求出对应几何体的体积，则两者体积之 和即该组合体的体积． 答案　B 解析　由俯视图，可知该几何体的底面由三角形和半圆两部分构成，结合正视图和侧视图可 知该几何体是由半个圆锥与一个三棱锥组合而成的，并且圆锥的轴截面与三棱锥的一个侧面 重合，两个锥体的高相等． 由三视图中的数据，可得该圆锥的底面半径 r＝6，三棱锥的底面是一个底边长为 12，高为 6 2 的等腰三角形，两个锥体的高 h＝ 122－62＝6 3， 故半圆锥的体积 V1＝1 2×1 3π×62×6 3＝36 3π. 三棱锥的底面积 S＝1 2×12×6＝36， 三棱锥的体积 V2＝1 3Sh＝1 3×36×6 3＝72 3. 故该几何体的体积 V＝V1＋V2＝36 3π＋72 3 ＝36 3(π＋2)．故选 B. 题型三　立体几何中的计算综合问题 例 3　(2014·陕西)四面体 ABCD 及其三视图如图所示，平行于棱 AD，BC 的平面分别交四面体 的棱 AB，BD，DC，CA 于点 E，F，G，H. (1)求四面体 ABCD 的体积； (2)证明：四面体 EFGH 是矩形． 破题切入点　由三视图和几何体得知原几何体中各元素的量和性质来求解． (1)解　由该四面体的三视图可知，BD⊥DC，BD⊥AD，AD⊥DC，BD ＝DC＝2，AD＝1， ∴AD⊥平面 BDC， ∴四面体 ABCD 体积 V＝1 3×1 2×2×2×1＝2 3. (2)证明　∵BC∥平面 EFGH，平面 EFGH∩平面 BDC＝FG，平面 EFGH∩平面 ABC＝EH， ∴BC∥FG，BC∥EH，∴FG∥EH. 同理 EF∥AD，HG∥AD，∴EF∥HG， ∴四边形 EFGH 是平行四边形， 又∵AD⊥平面 BDC，∴AD⊥BC，∴EF⊥FG. ∴四边形 EFGH 是矩形． 总结提高　(1)三视图的正视图、侧视图、俯视图分别是从几何体的正前方、正左方、正上方 观察几何体画出的轮廓线．画三视图的基本要求：正俯一样长，俯侧一样宽，正侧一样高． (2)三视图排列规则：俯视图放在正视图的下面，长度与正视图一样；侧视图放在正视图的右 面，高度和正视图一样，宽度与俯视图一样． (3)立体几何中有关表面积、体积的计算首先要熟悉几何体的特征，其次运用好公式，作好辅 3 助线等． 1．(2013·四川)一个几何体的三视图如图所示，则该几何体的直观图可以是(　　) 答案　D 解析　由三视图可知上部是一个圆台，下部是一个圆柱，选 D. 2．如图，网格纸上正方形小格的边长为 1(表示 1 cm)，图中粗线画出的是某零件的三视图， 该零件由一个底面半径为 3 cm，高为 6 cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原 来毛坯体积的比值为(　　) A.17 27 B.5 9 C.10 27 D.1 3 答案　C 解析　由三视图可知几何体是如图所示的两个圆柱的组合体．其中左面圆柱 的高为 4 cm，底面半径为 2 cm，右面圆柱的高为 2 cm，底面半径为 3 cm，则 组合体的体积 V1＝π×22×4＋π×32×2＝16π＋18π＝34π(cm 3)，原毛坯体积 V2＝π×32×6＝54π(cm3)，则所求比值为54π－34π 54π ＝10 27. 3．(2014·浙江)某几何体的三视图(单位：cm)如图所示，则此几何体的表面积是(　　) 4 A．90 cm2 B．129 cm2 C．132 cm2 D．138 cm2 答案　D 解析　该几何体如图所示，长方体的长、宽、高分别为 6 cm,4 cm，3 cm， 直三棱柱的底面是直角三角形，边长分别为 3 cm,4 cm,5 cm，所以表面积 S＝[2×(4×6＋4×3)＋3×6＋3×3]＋ (5 × 3＋4 × 3＋2 × 1 2 × 4 × 3) ＝99＋39＝138(cm2)． 4．(2014·重庆)某几何体的三视图如图所示，则该几何体的表面积为(　　) A．54 B．60 C．66 D．72 答案　B 解析　由俯视图可以判断该几何体的底面为直角三角形，由正视图和侧视图可以判断该几何 体是由直三棱柱(侧棱与底面垂直的棱柱)截取得到的．在长方体中分析还原，如图(1)所示，故 该几何体的直观图如图(2)所示．在图(1)中，直角梯形 ABPA1 的面积为1 2×(2＋5)×4＝14，计 算可得 A1P＝5.直角梯形 BCC1P 的面积为1 2×(2＋5)×5＝35 2 .因为 A1C1⊥平面 A1ABP，A1P⊂平 面 A1ABP，所以 A1C1⊥A1P，故 Rt△A1PC1 的面积为1 2×5×3＝15 2 . 又 Rt△ABC 的面积为1 2×4×3＝6，矩形 ACC1A1 的面积为 5×3＝15，故几何体 ABC－A1PC1 的表面积为 14＋35 2 ＋15 2 ＋6＋15＝60. 5．两球 O1 和 O2 在棱长为 1 的正方体 ABCD－A1B1C1D1 的内部，且互相外切，若球 O1 与过点 A 的正方体的三个面相切，球 O2 与过点 C1 的正方体的三个面相切，则球 O1 和球 O2 的表面积 5 之和的最小值为(　　) A．(6－3 3)π B．(8－4 3)π C．(6＋3 3)π D．(8＋4 3)π 答案　A 解析　设球 O1，O2 的半径分别为 r1，r2， 由题意知 O1A＋O1O2＋O2C1＝ 3， 而 O1A＝ 3r1，O1O2＝r1＋r2，O2C1＝ 3r2， ∵ 3r1＋r1＋r2＋ 3r2＝ 3.∴r1＋r2＝3－ 3 2 ， 从而 S1＋S2＝4πr21＋4πr22＝4π(r21＋r22) ≥4π· (r1＋r2)2 2 ＝(6－3 3)π. 6．已知球的直径 SC＝4，A，B 是该球球面上的两点，AB＝ 3，∠ASC＝∠BSC＝30°，则棱 锥 S—ABC 的体积为(　　) A．3 3 B．2 3 C. 3 D．1 答案　C 解析　如图，过 A 作 AD 垂直 SC 于 D，连接 BD. 由于 SC 是球的直径，所以∠SAC＝∠SBC＝90°，又∠ASC＝∠BSC ＝30°，又 SC 为公共边， 所以△SAC≌△SBC. 由于 AD⊥SC，所以 BD⊥SC. 由此得 SC⊥平面 ABD. 所以 VS—ABC＝VS—ABD＋VC—ABD＝1 3S△ABD·SC. 由于在 Rt△SAC 中，∠ASC＝30°，SC＝4， 所以 AC＝2，SA＝2 3，由于 AD＝SA·CA SC ＝ 3. 同理在 Rt△BSC 中也有 BD＝SB·CB SC ＝ 3. 又 AB＝ 3，所以△ABD 为正三角形， 所以 VS—ABC＝1 3S△ABD·SC＝1 3×1 2×( 3)2·sin 60°×4＝ 3，所以选 C. 7．(2014·辽宁)某几何体三视图如图所示，则该几何体的体积为(　　) 6 A．8－2π B．8－π C．8－π 2 D．8－π 4 答案　B 解析　这是一个正方体切掉两个1 4圆柱后得到的几何体， 如图，几何体的高为 2， V＝23－1 4×π×12×2×2＝8－π. 8．已知某几何体的三视图如图所示，其中正视图、侧视图均由直角三角形与半圆构成，俯视 图由圆与内接三角形构成，根据图中的数据可得几何体的体积为(　　) A. 2π 3 ＋1 2 B.4π 3 ＋1 6 C. 2π 6 ＋1 6 D.2π 3 ＋1 2 答案　C 解析　由三视图确定该几何体是一个半球体与三棱锥构成的组合体，如图， 其中 AP，AB，AC 两两垂直，且 AP＝AB＝AC＝1，故 AP⊥平面 ABC，S△ABC ＝1 2AB×AC＝1 2，所以三棱锥 P－ABC 的体积 V1＝1 3×S△ABC×AP＝1 3×1 2×1 ＝1 6，又 Rt△ABC 是半球底面的内接三角形，所以球的直径 2R＝BC＝ 2， 解得 R＝ 2 2 ，所以半球的体积 V2＝1 2×4π 3 ×( 2 2 )3＝ 2π 6 ，故所求几何体的体积 V＝V1＋V2＝1 6 7 ＋ 2π 6 . 9．(2014·北京)某三棱锥的三视图如图所示，则该三棱锥最长棱的棱长为________． 答案　2 2 解析　根据三视图还原几何体，得如图所示的三棱锥 P－ABC. 由三视图的形状特征及数据，可推知 PA⊥平面 ABC，且 PA＝2. 底面为等腰三角形，AB＝BC， 设 D 为 AC 的中点，AC＝2， 则 AD＝DC＝1，且 BD＝1， 易得 AB＝BC＝ 2，所以最长的棱为 PC， PC＝ PA2＋AC2＝2 2. 10．已知正三棱锥 P－ABC，点 P，A，B，C 都在半径为 3的球面上，若 PA，PB，PC 两两 相互垂直，则球心到截面 ABC 的距离为________． 答案　 3 3 解析　如图，作 PM⊥平面 ABC，设 PA＝a，则 AB＝ 2a，CM＝ 6 3 a， PM＝ 3 3 a. 设球的半径为 R， 所以 ( 3 3 a－R)2＋( 6 3 a )2＝R2， 将 R＝ 3代入上式， 解得 a＝2，所以 d＝ 3－2 3 3＝ 3 3 . 11．已知一个圆锥的底面半径为 R，高为 H，在其内部有一个高为 x 的内接圆柱． (1)求圆柱的侧面积； (2)x 为何值时，圆柱的侧面积最大？ 解　(1)作圆锥的轴截面，如图所示． 8 因为r R＝H－x H ，所以 r＝R－R Hx， 所以 S 圆柱侧＝2πrx ＝2πRx－2πR H x2(0

查看更多