高考试题——数学理北京卷及答案

高考试题——数学理北京卷及答案

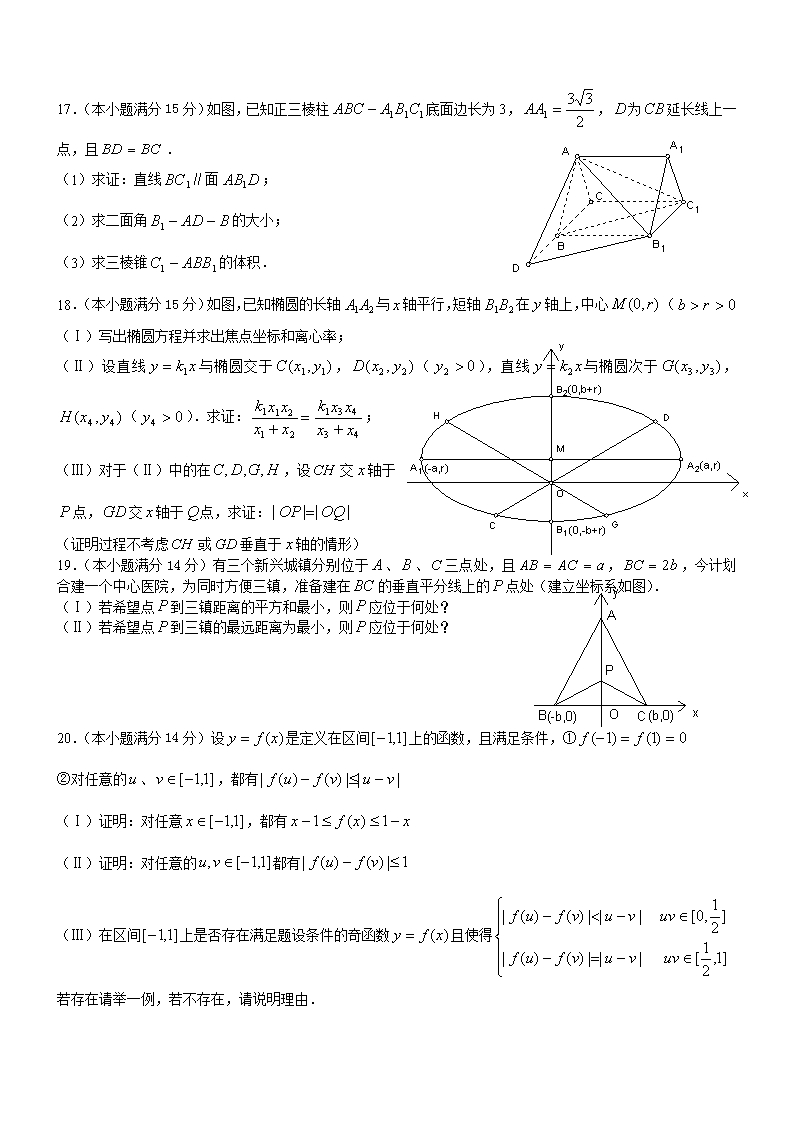
‎ 2003年普通高等学校招生全国统一考试（北京卷）数 学（理工农医类）‎ 第Ⅰ卷（选择题共50分）‎ 参考公式：‎ 三角函数的积化和差公式： 正棱台、圆台的侧面积公式 ‎ 其中、分别表示 ‎ 上、下底面周长，表示斜高或母线长.‎ ‎ 球体的体积公式： ，其中R ‎ ‎ 表示球的半径.‎ 一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合要求的.‎ ‎（1）设集合，，则等于 ‎（A）　（B）　　（C）　（D）或 ‎（2）设，，，则 ‎（A）　　（B）　　（C）　　（D）‎ ‎（3）“”是“”的 ‎（A）必要非充分条件　　（B）充分非必要条件 （C）充分必要条件　　（D）既非充分又非必要条件 ‎4．已知是平面，是直线，下列命题中不正确的是 ‎（A）若∥，，则∥　（B）若∥，，则 ‎（C）若，，则∥　　　（D）若，，则．‎ ‎5．极坐标方程表示的曲线是 ‎（A）圆　　　（B）椭圆　　　　（C）抛物线　　　（D）双曲线 ‎6．若，且，则的最小值是 ‎（A）2　　　　　（B）3　　　　　（C）4　　　　　（D）5‎ ‎7．如果圆台的母线与底面成角，那么这个圆台的侧面积与轴截面面积的比为 ‎（A）　　　　（B）　　　（C）　　　（D）‎ ‎8．从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种，分别种在不同土质的三块土地上，其中黄瓜必须种植．不同的种植方法共有 ‎（A）24种　　　　（B）18种　　　　（C）12种　　　　（D）6种 ‎9．若数列的通项公式是，，则等于 ‎（A）　　　（B）　　　　（C）　　　　　（D）‎ ‎10．某班试用电子投票系统选举班干部候选人．全班名同学都有选举权和被选举权，他们的编号分别为．规定：同意按“‎1”‎，不同意（含弃权）按“‎0”‎．令 其中，且，则同时同意第1、2号同学当选的人数为 ‎（A） （B）‎ ‎（C） （D）‎ 第Ⅱ卷（非选择题共100分）‎ 二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上.‎ ‎11．，，，其中 为偶函数．‎ ‎12．已知双曲线方程为，则以双曲线左顶点为顶点，右焦点为焦点的抛物线方程为 ．‎ ‎13．一底面半径为的圆柱，被一平面所截剩下部分母线最大值为，最小值为，那么圆柱被截后剩下部分的体积为 ．‎ ‎14．一根长为1的铁丝，分成两段分别围成一个正方形和一个圆，当正方形和圆的面积之和最小时，正方形的周长为 ．‎ 三、解答题：本大题共6小题，共84分.解答应写出文字说明，证明过程或演算步骤.‎ ‎15．（本小题满分13分）已知函数 ‎（Ⅰ）求的最小正周期；‎ ‎（Ⅱ）求在区间上的最大值和最小值. ‎ ‎16．（本小题满分13分）已知数列是等差数列，且，‎ ‎（1）求数列的通项公式；‎ ‎（2）设数列（），求数列的前项和公式.‎ ‎17．（本小题满分15分）如图，已知正三棱柱底面边长为3，，为延长线上一点，且．‎ ‎（1）求证：直线∥面；‎ ‎（2）求二面角的大小；‎ ‎（3）求三棱锥的体积．‎ ‎18．（本小题满分15分）如图，已知椭圆的长轴与轴平行，短轴在轴上，中心（‎ ‎（Ⅰ）写出椭圆方程并求出焦点坐标和离心率；‎ ‎（Ⅱ）设直线与椭圆交于，（），直线与椭圆次于，（）．求证：；‎ ‎（Ⅲ）对于（Ⅱ）中的在，设交轴于 点，交轴于点，求证：‎ ‎（证明过程不考虑或垂直于轴的情形）‎ ‎19．（本小题满分14分）有三个新兴城镇分别位于、、三点处，且，，今计划合建一个中心医院，为同时方便三镇，准备建在的垂直平分线上的点处（建立坐标系如图）．‎ ‎（Ⅰ）若希望点到三镇距离的平方和最小，则应位于何处？‎ ‎（Ⅱ）若希望点到三镇的最远距离为最小，则应位于何处？‎ ‎20．（本小题满分14分）设是定义在区间上的函数，且满足条件，①‎ ‎②对任意的、，都有 ‎（Ⅰ）证明：对任意，都有 ‎（Ⅱ）证明：对任意的都有 ‎（Ⅲ）在区间上是否存在满足题设条件的奇函数且使得 若存在请举一例，若不存在，请说明理由．‎ ‎2003年普通高等学校招生全国统一考试(北京卷) ‎ 数学（理工农医类）答案 一、选择题：本题考查基本知识和基本运算. 每小题5分，满分50分.‎ ‎1．A 2．D 3．A 4．B 5．D 6．B 7．C 8．B 9．C 10．C 二、填空题：本题考查基本知识和基本运算.每小题4分,满分16分.‎ ‎11． 12． 13． 14．‎ 三、解答题：本大题共6小题，共84分.解答应写出文字说明，证明过程或演算步骤.‎ ‎15．本小题主要考查三角函数的倍角、和角公式，以及三角函数的性质等基本知识，考查运算能力，满分13分. ‎ ‎（Ⅰ）解：因为 所以的最小正周期 ‎（Ⅱ）解：因为,所以 当时，取最大值为,‎ 当时，取最小值为－1‎ ‎∴的最大值为1,最小值为－‎ ‎16．本小题主要考查等差、等比数列等基本知识，考查综合运用数学知识和方法解决问题的能力.满分13分.‎ ‎ （Ⅰ）解：设数列公差为，则 又 所以 ‎（Ⅱ）解：由得 ‎ ① ‎ ‎②‎ ‎ 当x≠1时，将①式减去②式，得 ‎ ‎ ‎∴‎ 当x=1时，‎ ‎ 综上可知，当x=1时，‎ ‎ 当x≠1时，‎ ‎17．本小题主要考查直线与平面的位置关系，正棱柱的性质，棱锥的体积等基本知识，考查空间想象能力和逻辑推理能力. 满分15分.‎ ‎（Ⅰ）证明：∵CD∥C1B1 ，又BD=BC=B‎1C1，‎ ‎∴四边形BDB‎1C1是平行四边形 ‎∴BC1∥DB1 ‎ 又DB1平面AB1D，BC1平面AB1D ‎∴直线BC1∥平面AB1D ‎（Ⅱ）解：过B作BE⊥AD于E，连结EB1，‎ ‎ ∵ BB1⊥平面ABD ‎ ∴ B1E⊥AD ‎ ∴ ∠B1EB是二面角B1—AD—B的平面角 ‎ ∵ BD=BC=AB ‎ ∴ E是AD的中点，‎ ‎ ∴ BE=AC=‎ 在RtB1BE中，tan∠B1EB=‎ ‎ ∴ ∠B1EB=‎ ‎ 即二面角B1—AD—B的大小为 ‎ （Ⅲ）解法一：过A作AF⊥BC于F，‎ ‎ ∵ BB1⊥平面ABC，‎ ‎ ∴ 平面ABC⊥平面BB‎1C1C，‎ ‎ ∴ AF⊥平面BB‎1C1C 且AF=‎ ‎ ∴ ==‎ ‎ =‎ ‎=‎ ‎ 即三棱锥C1—ABB1的体积为 ‎18．本小主要考查直线、椭圆和双曲线等基本知识，考查分析问题和解决问题的能力.满分15分.‎ ‎ （Ⅰ）解：椭圆方程为 ‎ 焦点坐标为，‎ ‎ 离心率 ‎（Ⅱ）证明：证明：将直线CD的方程代入椭圆方程，得 ‎ ‎ ‎ 整理得 ‎ ‎ ‎ 根据韦达定理，得 ‎ ，，‎ ‎ 所以 ①‎ ‎ 将直线GH的方程代入椭圆方程，同理可得 ‎ ②‎ ‎ 由 ①、②得 = ‎ ‎ 所以结论成立 ‎（Ⅲ）证明：设点P，点Q ‎ 由C、P、H共线，得 ‎ ‎ 解得 ‎ ‎ 由D、Q、G共线，同理可得 ‎ ‎ ‎ ‎ 由 = 变形得 ‎ =‎ ‎ 所以 ‎ ‎ 即 ‎ ‎19．本小题主要考查函数，不等式等基本知识，考查运用数学知识分析问题和解决问题的能力.满分14分.‎ ‎ （Ⅰ）解：由题设条件a>b>0,设P的坐标为（0，），则P至三镇距离的平方和为 ‎ =‎ 所以，当时，函数取得最小值. ‎ 答:点P的坐标是 ‎（Ⅱ）解：记 P至三镇的最远距离为 ‎ ‎ 由解得记 于是 ‎ ‎ 当，即时，‎ 因为在[上是增函数，而上是减函数. ‎ 所以时,函数取得最小值. 点P的坐标是 当，即时，因为在[上当y=0函数取得最小值b，而上是减函数,且 ，所以时, 函数取得最小值. ‎ 答：当时，点P的坐标是 ‎ 当时，点P的坐标是，其中 ‎20．本小题考查函数、不等式等基本知识，考查综合运用数学知识分析问题和解决问题的能力.满分14分.‎ ‎（Ⅰ）证明：由题设条件可知，‎ 当时，有即 ‎（Ⅱ）对任意的，‎ 当 当不妨设 则 从而有 总上可知，对任意的，都有 ‎（Ⅲ）答：这样满足所述条件的函数不存在.理由如下：‎ ‎ 假设存在函数满足条件，则由 得 又，所以 ①‎ ‎ 又因为为奇函数，所以，‎ 由条件 得 所以 ② ‎ ‎ ①与②矛盾，因此假设不成立，即这样的函数不存在.‎