高三数学综合试卷及答案高考题组合

高三数学综合试卷及答案高考题组合

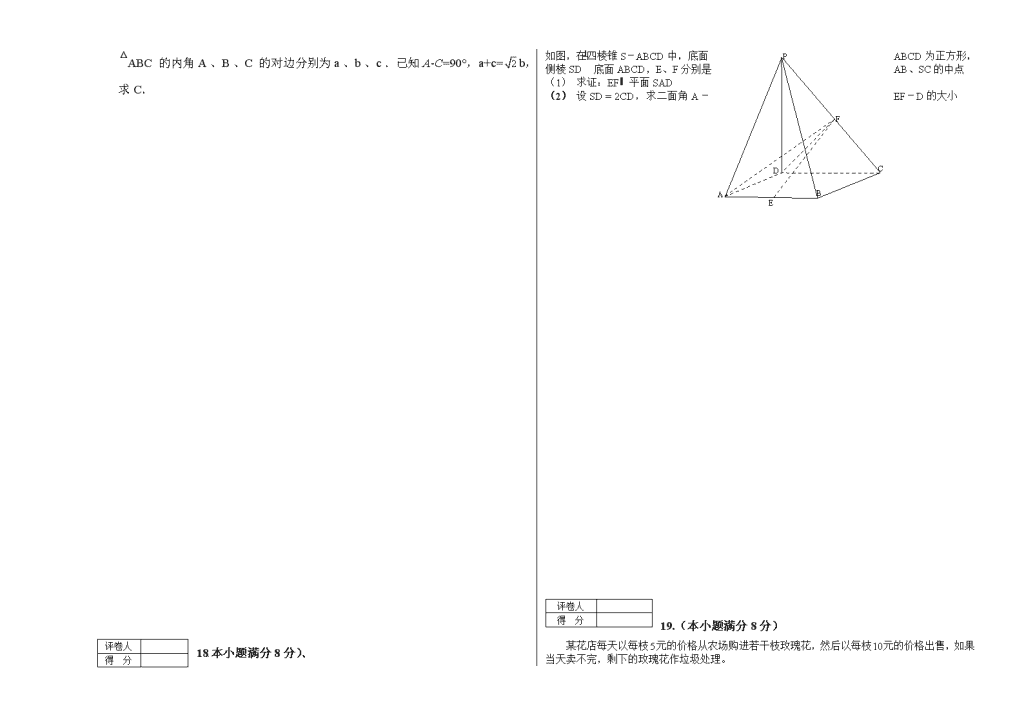
座号 高中教师招考试卷（数学）‎ 总分100分 时间2小时 题目 第一题 第二题 ‎17‎ ‎18‎ ‎19‎ ‎20‎ ‎21‎ ‎22‎ 得分 评卷人 得　分 第一大题：选择题，本题共12个小题，每小题3分，共计36分。‎ ‎1．sin2100 =‎ ‎(A) (B) - (C) (D) -‎ ‎2．函数f(x)=|sinx|的一个单调递增区间是 ‎(A)（－，） (B) （，） (C) （p，） (D) （，2p）‎ ‎3．设复数z满足=i，则z =‎ ‎ (A) -2+i (B) -2-i (C) 2-i (D) 2+i ‎4．不等式:>0的解集为 ‎(A)( -2, 1) (B) ( 2, +∞)‎ ‎(C) ( -2, 1)∪ ( 2, +∞) (D) ( -∞, -2)∪ ( 1, +∞)‎ ‎5．已知正三棱柱ABC－A1B‎1C1的侧棱长与底面边长相等，则AB1与侧面ACC‎1A1所成角的正弦等于 ‎(A) (B) (C) (D) ‎ ‎6．已知曲线的一条切线的斜率为,则切点的横坐标为 ‎(A)3 (B) 2 (C) 1 (D) ‎7．把函数y=ex的图象按向量a=(2,3)平移，得到y=f(x)的图象，则f(x)=‎ ‎(A) ex-3+2 (B) ex+3－2 (C) ex-2+3 (D) ex+2－3‎ ‎8．某同学有同样的画册2本，同样的集邮册3本，从中取出4本赠送给4位朋友每位朋友1本，则不同的赠送方法共有 ‎ A．4种 B．10种 C．18种 D．20种 ‎9．已知抛物线C：的焦点为F，直线与C交于A，B两点．则=‎ A． B． C． D． ‎ ‎10．已知为等比数列，，，则 ‎ ‎ ‎11．设变量满足约束条件：，则的最小值=‎ A． B． C． D．‎ ‎12. （8）等轴双曲线的中心在原点，焦点在轴上，与抛物线的准线交于 两点，；则的实轴长为（ ）‎ ‎ ‎ 评卷人 得　分 第二大题、填空题，本题共4个小题，每小题4分，共16分。‎ 13．设向量，若向量与向量共线，则 ．‎ ‎14．设曲线在点处的切线与直线垂直，则 ．‎ ‎15.已知a∈（，），sinα=，则tan2α= ‎ ‎16. 某个部件由三个元件按下图方式连接而成，元件1或元件2正常工作，且元件3‎ 正常工作，则部件正常工作，设三个电子元件的使用寿命（单位：小时）均服从 正态分布，且各个元件能否正常相互独立，那么该部件的使用寿命 超过1000小时的概率为 ‎ 评卷人 得　分 第三大题、‎ ‎17．（本小题满分8分）‎ ‎ △ABC的内角A、B、C的对边分别为a、b、c．己知 A-C=90°，a+c=b，求C． ‎ 评卷人 得　分 ‎18.本小题满分8分）、‎ A B C D P E F 如图，在四棱锥S－ABCD中，底面ABCD为正方形，侧棱SD⊥ 底面ABCD，E、F分别是AB、SC的中点 （1） 求证：EF∥ 平面SAD （2） 设SD = 2CD，求二面角A－EF－D的大小 评卷人 得　分 ‎19.（本小题满分8分）‎ 某花店每天以每枝元的价格从农场购进若干枝玫瑰花，然后以每枝元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理。‎ ‎（1）若花店一天购进枝玫瑰花，求当天的利润(单位：元)关于当天需求量（单位：枝，）的函数解析式。 ‎ ‎（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：‎ 以100天记录的各需求量的频率作为各需求量发生的概率。‎ ‎（i）若花店一天购进枝玫瑰花，表示当天的利润（单位：元），求的分布列，‎ 数学期望及方差；‎ ‎（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？‎ 请说明理由。‎ 评卷人 得　分 ‎20（本小题满分8分）‎ 已知是首项为19，公差为-2的等差数列，为的前项和.‎ ‎（Ⅰ）求通项及；‎ ‎（Ⅱ）设是首项为1，公比为3的等比数列，求数列的通项公式及其前项和.‎ 评卷人 得　分 ‎21（本小题满分8分） ‎ 已知椭圆的离心率为，过右焦点F的直线与相交于、‎ 两点，当的斜率为1时，坐标原点到的距离为 ‎ （I）求，的值；‎ ‎ （II）上是否存在点P，使得当绕F转到某一位置时，有成立？‎ 若存在，求出所有的P的坐标与的方程；若不存在，说明理由。‎ 评卷人 得　分 ‎22（本小题满分8分）‎ 已知函数满足满足；‎ 求的解析式及单调区间；‎ 第一题选择题 DCCCA, ‎ACADD‎, ‎DC 第二题 ‎(13), 2 (14), 2, (15), (16), ‎ 第三题 ‎, 17．解：由及正弦定理可得 ‎ …………3分 ‎ 又由于故 ‎ ‎ ‎ ‎ ‎ …………6分 ‎ ‎ ‎ ‎ ‎ 因为，‎ ‎ 所以 C=15 0 8分 A E B C F S D H G M ‎18．解法一：‎ ‎（1）作交于点，则为的中点．‎ 连结，又，‎ 故为平行四边形．‎ ‎，又平面平面．‎ 所以平面．………………4分 ‎（2）不妨设，则为等 腰直角三角形． ‎ 取中点，连结，则．‎ 又平面，所以，而，‎ 所以面． ………….6分 取中点，连结，则．‎ 连结，则．‎ 故为二面角的平面角 A A E B C F S D G M y z x ‎ ．‎ 所以二面角的大小为．…….. 8分 解法二：（1）如图，建立空间直角坐标系．‎ 设，则 ‎，‎ ‎． ………2分 取的中点，则．‎ 平面平面，‎ 所以平面．………4分 ‎（2）不妨设，则．‎ 中点 又，，……………6分 所以向量和的夹角等于二面角的平面角．‎ ‎ ．……. ……‎ 所以二面角的大小为．…………. 8分 ‎19【解析】（1）当时，‎ ‎ 当时，‎ ‎ 得：………4分 ‎ （2）（i）可取，，‎ ‎ ‎ ‎ 的分布列为 ‎ ‎ ‎ …………6分 ‎ （ii）购进17枝时，当天的利润为 ‎ 得：应购进17枝……………8分 ‎20解 ‎21,解 :(I）设，直线，由坐标原点到的距离为 ‎ 则，解得 .又…. 4分 ‎（II）由(I）知椭圆的方程为.设、‎ 由题意知的斜率为一定不为0，故不妨设 ‎ 代入椭圆的方程中整理得，显然。‎ 由韦达定理有：．．．．．．．．①6分 ‎.假设存在点P，使成立，则其充要条件为：‎ 点，点P在椭圆上，即。‎ 整理得。‎ 又在椭圆上，即.‎ 故．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．②‎ 将及①代入②解得 ‎,=,即.7分 当;‎ 当.8分 ‎22,【解析】（1）‎ ‎ 令得：…………….. 2分 ‎ ‎ ‎ 得：……4分 ‎ 在上单调递增 ‎ ‎ ‎ 得：的解析式为 ‎ 且单调递增区间为，单调递减区间为…. 8分 ‎ ‎