2015高考数学人教A版本(5-4向量的应用及向量与其他知识的综合问题)一轮复习学案
【走向高考】2015届高考数学一轮总复习 5-4向量的应用及向量与其他知识的综合问题课后强化作业 新人教A版
基础巩固强化
一、选择题
1.(文)如图,在△ABC中,AB=5,BC=3,CA=4,且O是△ABC的外心,则·=( )
A.6 B.-6 C.8 D.-8
[答案] D
[解析] ∵AB2=AC2+BC2,∴∠ACB为直角,
∵O为△ABC外心,
∴·=-·=-(+)·
=-||2-·=-8.
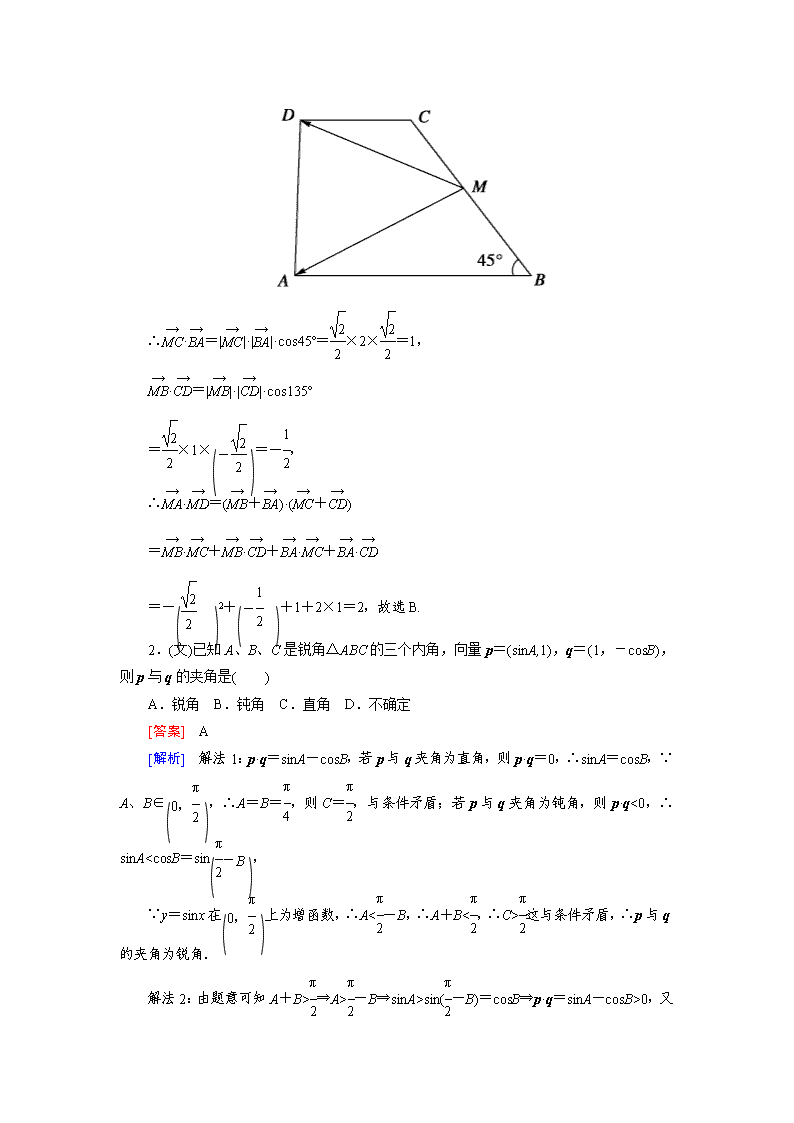
(理)在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=2,M为腰BC的中点,则·=( )
A.1 B.2 C.3 D.4
[答案] B
[解析] 由条件知AB=2,CD=1,BC=,
∴MB=MC=,
∴·=||·||·cos45°=×2×=1,
·=||·||·cos135°
=×1×=-,
∴·=(+)·(+)
=·+·+·+·
=-2++1+2×1=2,故选B.
2.(文)已知A、B、C是锐角△ABC的三个内角,向量p=(sinA,1),q=(1,-cosB),则p与q的夹角是( )
A.锐角 B.钝角 C.直角 D.不确定
[答案] A
[解析] 解法1:p·q=sinA-cosB,若p与q夹角为直角,则p·q=0,∴sinA=cosB,∵A、B∈,∴A=B=,则C=,与条件矛盾;若p与q夹角为钝角,则p·q<0,∴sinA
这与条件矛盾,∴p与q的夹角为锐角.
解法2:由题意可知A+B>⇒A>-B⇒sinA>sin(-B)=cosB⇒p·q=sinA-cosB>0,又显然p、q不同向,故p与q夹角为锐角.
(理)(2013·乌鲁木齐第一次诊断)△ABC中,若(+)·=||2,则的值为( )
A.2 B.4 C. D.2
[答案] B
[解析] 设△ABC中,a,b,c分别是角A,B,C所对的边,由(+)·=||2得,·+·=||2,即bccos(π-A)+accosB=c2,∴acosB-bcosA=c,由正弦定理得sinAcosB-cosAsinB=sinC=sin(A+B)=(sinAcosB+cosAsinB),即sinAcosB=4cosAsinB,∴=4.
3.(文)如果A是抛物线x2=4y的顶点,过点D(0,4)的直线l交抛物线x2=4y于B、C两点,那么·等于( )
A. B.0 C.-3 D.-
[答案] B
[解析] 由题意知A(0,0),设B(x1,y1),C(x2,y2),直线l:y=kx+4,
由消去y得,x2-4kx-16=0,
∴x1+x2=4k,x1x2=-16,
∴y1·y2=(kx1+4)(kx2+4)=k2x1x2+4k(x1+x2)+16=-16k2+16k2+16=16,
∴·=x1x2+y1y2=0.
(理)(2014·襄阳一中检测)过双曲线-=1(a>0,b>0)的一个焦点F作一条渐近线的垂线,垂足为点A,且与另一条渐近线交于点B,若=2,则此双曲线的离心率为( )
A. B. C. D.2
[答案] D
[解析] 设∠FOA=α,∵OA⊥FB,且=2,∴OA为FB的中垂线,∴∠FOB=2α,∵tanα=,tan2α=-,
∴=-,∴()2=3,∴=3,
∴e==2.
4.(2012·河北郑口中学模拟)已知P是△ABC所在平面内一点,++2=0,现将一粒黄豆随机撒在△ABC内,则黄豆落在△PBC内的概率是( )
A. B. C. D.
[答案] C
[解析] 如图,+==2,∵++2=0,∴+=0,∴P为AD的中点,
∴所求概率为P==.
5.(文)已知向量=(2,2),=(4,1),在x轴上有一点P,使·有最小值,则P点坐标为( )
A.(-3,0) B.(3,0)
C.(2,0) D.(4,0)
[答案] B
[解析] 设P(x,0),则=(x-2,-2),=(x-4,-1),·=(x-2)(x-4)+(-2)×(-1)=x2-6x+10=(x-3)2+1,∴当x=3时·有最小值,
∴P(3,0).
(理)直线ax+by+c=0与圆x2+y2=9相交于两点M、N,若c2=a2+b2,则·(O为坐标原点)等于( )
A.-7 B.-14 C.7 D.14
[答案] A
[解析] 记、的夹角为2θ.依题意得,圆心(0,0)到直线ax+by+c=0的距离等于=1,∴cosθ=,∴cos2θ=2cos2θ-1=2×()2-1=-,∴·=3×3cos2θ=-7,选A.
6.(2013·荆州市质检)在△ABC中,AB=2,AC=4,若点P为△ABC的外心,则·的值为( )
A.2 B.4 C.6 D.8
[答案] C
[解析] ∵cos∠BAP===,∴·=||·||cos∠BAP=,同理·=,∵=-,∴·=·-·=-=-=6.
二、填空题
7.(文)
(2012·宁夏三市联考)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则·=________.
[答案] -
[解析] ·=(+)·(-)=||2-||2-·=1-2-×1×2·cos60°=-.
(理)
如图,半圆的直径AB=6,O为圆心,C为半圆上不同于A、B的任意一点,若P为半径OC上的动点,则(+)·的最小值为________.
[答案] -
[解析] 设PC=x,则0≤x≤3.(+)·=2·=-2x×(3-x)=2x2-6x=2(x-)2-,所以(+)·的最小值为-.
8.(2013·山西诊断)已知△ABC中,角A、B、C的对边分别是a、b、c,且tanB=,·=,则tanB=________.
[答案] 2-
[解析] 依题意及余弦定理得(a2+c2-b2)tanB=2accosB·tanB=2acsinB=2-,又·=accosB=,于是有=2-,即tanB=2-.
9.(2013·云南文山一模)在△ABC中,AB=2,AC=1,=,则·的值为________.
[答案] -
[解析] ∵=,∴D为BC的中点,∴=(+),==(-),·=(2-2)=-.
三、解答题
10.(文)(2014·树德中学检测)已知向量=(2cosx+1,cos2x-sinx+1),=(cosx,-1),f(x)=·.
(1)求函数f(x)的最小正周期;
(2)当x∈[0,]时,求函数f(x)的最大值及取得最大值时的x值.
[解析] (1)∵=(2cosx+1,cos2x-sinx+1),=(cosx,-1),
∴f(x)=·=(2cosx+1)cosx-(cos2x-sinx+1)
=2cos2x+cosx-cos2x+sinx-1
=cosx+sinx=sin(x+),
∴函数f(x)最小正周期T=2π.
(2)∵x∈[0,],
∴x+∈[,],
∴当x+=,
即x=时,f(x)=sin(x+)取到最大值.
(理)(2014·漳县二中月考)已知向量a=(sinθ,cosθ)与b=(,1),其中θ∈(0,).
(1)若a∥b,求sinθ和cosθ的值;
(2)若f(θ)=(a+b)2,求f(θ)的值域.
[解析] (1)∵a∥b,∴sinθ·1-cosθ=0,
求得tanθ=.
又∵θ∈(0,),∴θ=.∴sinθ=,cosθ=.
(注:本问也可以结合sin2θ+cos2θ=1或化为2sin(θ-)=0来求解)
(2)f(θ)=(sinθ+)2+(cosθ+1)2
=2sinθ+2cosθ+5=4sin(θ+)+5,
又∵θ∈(0,),θ+∈(,),
0)的焦点,A、B、C为该抛物线上三点,若++=0,||+||+||=3,则该抛物线的方程是( )
A.y2=2x B.y2=4x
C.y2=6x D.y2=8x
[答案] A
[解析] ∵F(,0),设A(x1,y1),B(x2,y2),C(x3,y3),
由++=0得,
(x1-)+(x2-)+(x3-)=0,
∴x1+x2+x3=p.
又由抛物线定义知,
||+||+||=(x1+)+(x2+)+(x3+)=3p=3,∴p=1,
因此,所求抛物线的方程为y2=2x,故选A.
(理)设F1、F2为椭圆+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,·的值等于( )
A.0 B.2 C.4 D.-2
[答案] D
[解析] 由题意得c==,
又S四边形PF1QF2=2S△PF1F2=2××F1F2·h (h为F1F2边上的高),所以当h=b=1时,S四边形PF1QF2取最大值,此时∠F1PF2=120°.
所以·=||·||·cos120°
=2×2×(-)=-2.
13.(2012·浙江省样本学校测试)如图,△ABC的外接圆的圆心为O,AB=3,AC=5,BC=,则·等于( )
A.-8 B.-1 C.1 D.8
[答案] D
[解析]
取BC的中点M,连接AM、OM,
·=(+)·=·
=·(-)==8,故选D.
二、填空题
14.(2013·兰州名校检测)设向量a=(a1,a2),b=(b1,b2),定义一种向量积a⊗b=(a1b1,a2b2),已知向量m=(2,),n=(,0),点P(x,y)在y=sinx的图象上运动.Q是函数y=f(x)图象上的点,且满足=m⊗+n(其中O为坐标原点),则函数y=f(x)的值域是________.
[答案] [-,]
[解析] 令Q(c,d),由新的运算可得=m⊗+n=(2x,sinx)+(,0)=(2x+,sinx),,消去x得d=sin(c-),所以y=f(x)=sin(x-),易知y=f(x)的值域是[-,].
15.(文)已知M是△ABC内的一点,且·=2,∠BAC=30°,若△MBC、△MCA和△MAB的面积分别为、x、y,则+的最小值是________.
[答案] 18
[解析] ∵·=2,∴bccosA=2,
∵∠BAC=30°,∴bc=4,
∴S△ABC=1,∴x+y=,
+=+=(+)+10≥18.
等号成立时,∴x=,y=,
∴在时,+取得最小值18.
(理)过双曲线-=1(a>0,b>0)的左焦点F(-c,0)(c>0),作圆x2+y2=的切线,切点为E,延长FE交双曲线右支于点P,若=(+),则双曲线的离心率为________.
[答案]
[解析] ∵PF与圆x2+y2=相切,∴OE⊥PF,且OE=,∵=(+),∴E为PF的中点,又O为FF2的中点,∴|PF2|=2|OE|=a,由双曲线定义知,|PF|=|PF2|+2a=3a,在Rt△PFF2中,|PF|2+|PF2|2=|FF2|2,∴a2+9a2=4c2,∴e2=,
∵e>1,∴e=.
三、解答题
16.(文)(2013·衡水中学六模)在平面直角坐标系中,已知点A(,0),向量e=(0,1),点B为直线x=-上的动点,点C满足2=+,点M满足·e=0,·=0.
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在y轴上,圆(x-1)2+y2=1内切于△PRN,求△PRN的面积的最小值.
[解析] (1)设M(x,y),B(-,m),则=(x+,y-m),
∵2=+=(,0)+(-,m)=(0,m),
∴C(0,),
e=(0,1),=(x,y-),=(-1,m),
由·e=0,·=0得消去m得y2=2x.
所以动点M的轨迹E的方程为y2=2x.
(2)设P(x0,y0),R(0,b),N(0,c),且b>c,
∴lPR:y=x+b,
即lPR:(y0-b)x-x0y+x0b=0,
由直线PR与圆相切得,=1,注意到x0>2,化简得(x0-2)b2+2y0b-x0=0,
同理得(x0-2)c2+2y0c-x0=0,
所以b,c是方程(x0-2)x2+2y0x-x0=0的两根,
所以|b-c|==,
有S△PRN=··x0=(x0-2)++4≥8,当x0=4时△PRN的面积的最小值为8.
(理)(2013·哈尔滨九中月考)如图,已知直线l与抛物线x2=4y相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
(1)若动点M满足·+||=0,求点M的轨迹C;
(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
[解析] (1)由x2=4y得y=x2,∴y′=x.
∴直线l的斜率为y′|x=2=1,
故直线l的方程为y=x-1,∴点A坐标为(1,0).
设M(x,y),则=(1,0),=(x-2,y),=(x-1,y),
由·+||=0得(x-2)+y·0+·=0,
整理,得+y2=1.
∴动点M的轨迹C为以原点为中心,焦点在x轴上,长轴长为2,短轴长为2的椭圆.
(2)由题意知直线l′的斜率存在且不为零,
设l′的方程为y=k(x-2)(k≠0)①,
将①代入+y2=1中,整理得(2k2+1)x2-8k2x+(8k2-2)=0,
由Δ>0得0
查看更多