- 2021-05-13 发布 |
- 37.5 KB |
- 3页


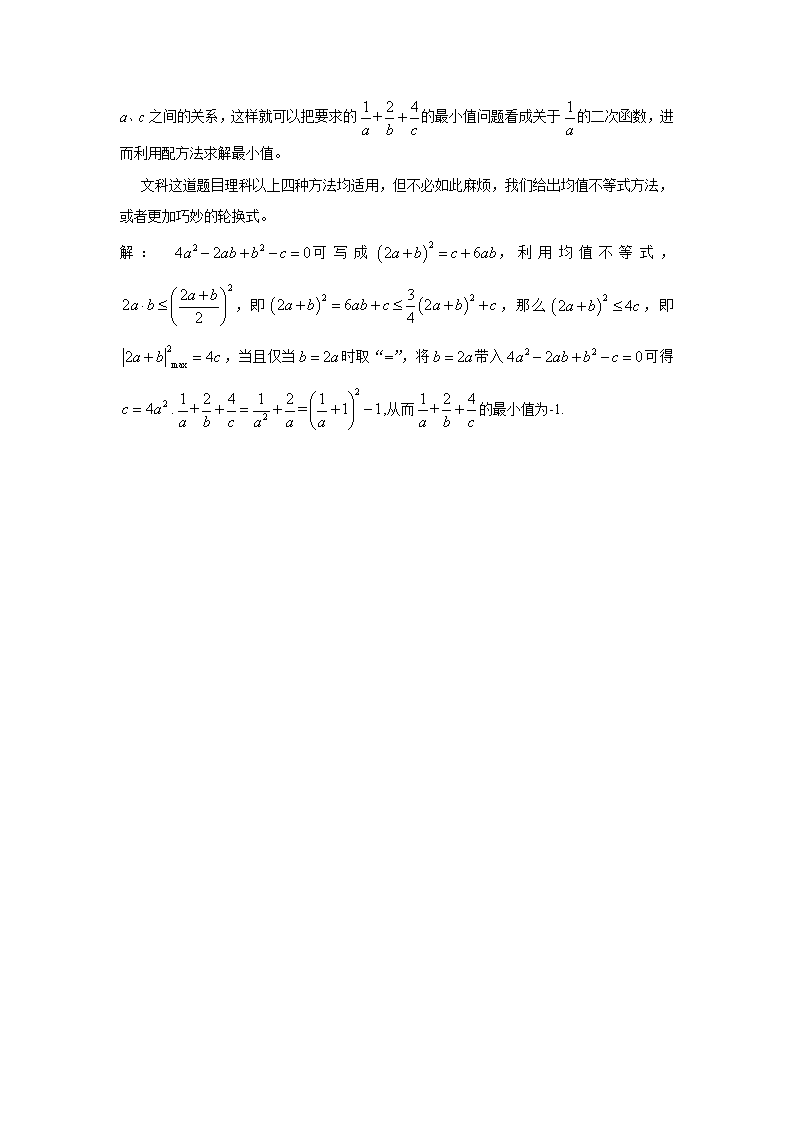
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
辽宁高考数学文理题的几种解法
2014 年辽宁高考数学(文、理)16 题的几种解法 大连 48 中学-----何兆强 下面我们给出 2014 年辽宁高考数学(文、理)16 题的几种解法,展现思维 的全过程和不同方法技巧。 (理)16. 对于 0c ,当非零实数 a,b 满足 2 24 2 4 0a ab b c ,且使| 2 |a b 最 大时, 3 4 5 a b c 的最小值为 . (文)16. 对于 0c ,当非零实数 a,b 满足 2 24 2 0a ab b c ,且使| 2 |a b 最 大时, 1 2 4+a b c 的最小值为 . 题目(理)拿到手后,分析已知条件,关键是找到 a、b 之间的关系、a、c 之间的关系, 这样就可以把要求的 3 4 5 a b c 的最小值问题看成关于 1 a 的二次函数,进而利用配方法求解 最小值。 方法一:设置 a、b 关系法 解:设b a ,带入 2 24 2 4 0a ab b c ,得到 2 24 2 4 ca ①,不妨将| 2 |a b 平方,再讲①带入,可得: 2 22 2 2 2 2 1| 2 | 2 24 184 2 4 422 a b a c c ,由二次函数特点,显然 当 1 3=2 8 时,即 2= 3 时| 2 |a b 有最大值,此时说明 2 3b a ②. 将 2= 3 带入①知, 240 9c a ③ 再将②、③带入 3 4 5 a b c ,整理可得, 2 2 3 4 5 9 3 9 1 4= 28 8 3a b c a a a ,从而 3 4 5 a b c 的最小值为-2. 方法二:方程法 解: 2 24 2 4 0a ab b c 可变形为 226 3 2 2 0b a b b a b c ,把此式看成 关于 b 的一元二次方程,必有解。由根的判别式可得: 2 2=9 2 24 2 0a b a b c ,解得: 2 242 15a b c ,显然 2 max 24| 2 | 15a b c , 讲其写成 215 2 24 a bc ①后带入 2 24 2 4 0a ab b c 中可得: 22 24 6 9 = 2 3 0a ab b a b ,从而得到说明 2 3b a ②,将②带入①得 240 9c a ,以 下同方法一。 方法三:数形结合法 解:把二元二次方程 2 24 2 4 0a ab b c (c 为常数)看成某条曲线,把 | 2 || 2 | 5 5 a ba b 看成曲线上一点 ,a b 到直线 2 0a b 距离的 5 倍,由此问题可 转化成曲线上一点到直线的最大距离问题。平移直线 2 0a b 直至与曲线 2 24 2 4 0a ab b c 相切,基于这种想法,我们需要联系方程组, 2 24 2 4 0 2 a ab b c b a m ,消去变量 b,得到关于 a 的一元二次方程, 2 224 18 4 0a m a m c ,令 2 2324 4 24 4 0m m c ,即 28 5c m ①,而 方程 2 224 18 4 0a m a m c 的唯一解是 3 8 ma ②,即 8 3m a 带入 2b a m 中 可得 2 3b a ,再由①、②可得 240 9c a ③,以下同方法一。 方法四:柯西不等式法 解: 2 24 2 4 0a ab b c 可变形为: 2 215 4 4 16 c ba b ,由柯西不等式知, 22 22 22 2 26 15 6 6 152 + 2 + 2 24 4 16 4 415 15 15 c b ba b a b a b ,即 2 242 15a b c ,当且仅当 15 4 4 62 15 ba b 时取“=”,即 2 3b a ,带入 2 24 2 4 0a ab b c 中,可得 240 9c a ,以下同方法一。 题目(文)拿到手后,分析已知条件,关键是利用均值不等式找到 a、b 之间的关系、a、 c 之间的关系,这样就可以把要求的 1 2 4+a b c 的最小值问题看成关于 1 a 的二次函数,进而 利用配方法求解最小值。 文科这道题目理科以上四种方法均适用,但不必如此麻烦,我们给出均值不等式方法, 或者更加巧妙的轮换式。 解 : 2 24 2 0a ab b c 可 写 成 22 6a b c ab , 利 用 均 值 不 等 式 , 222 2 a ba b ,即 2 232 6 24a b ab c a b c ,那么 22 4a b c ,即 2 max2 4a b c ,当且仅当 2b a 时取“=”,将 2b a 带入 2 24 2 0a ab b c 可得 24c a . 2 2 1 2 4 1 2 1+ = 1 1a b c a a a ,从而 1 2 4+a b c 的最小值为-1.查看更多