- 2021-05-13 发布 |
- 37.5 KB |
- 4页
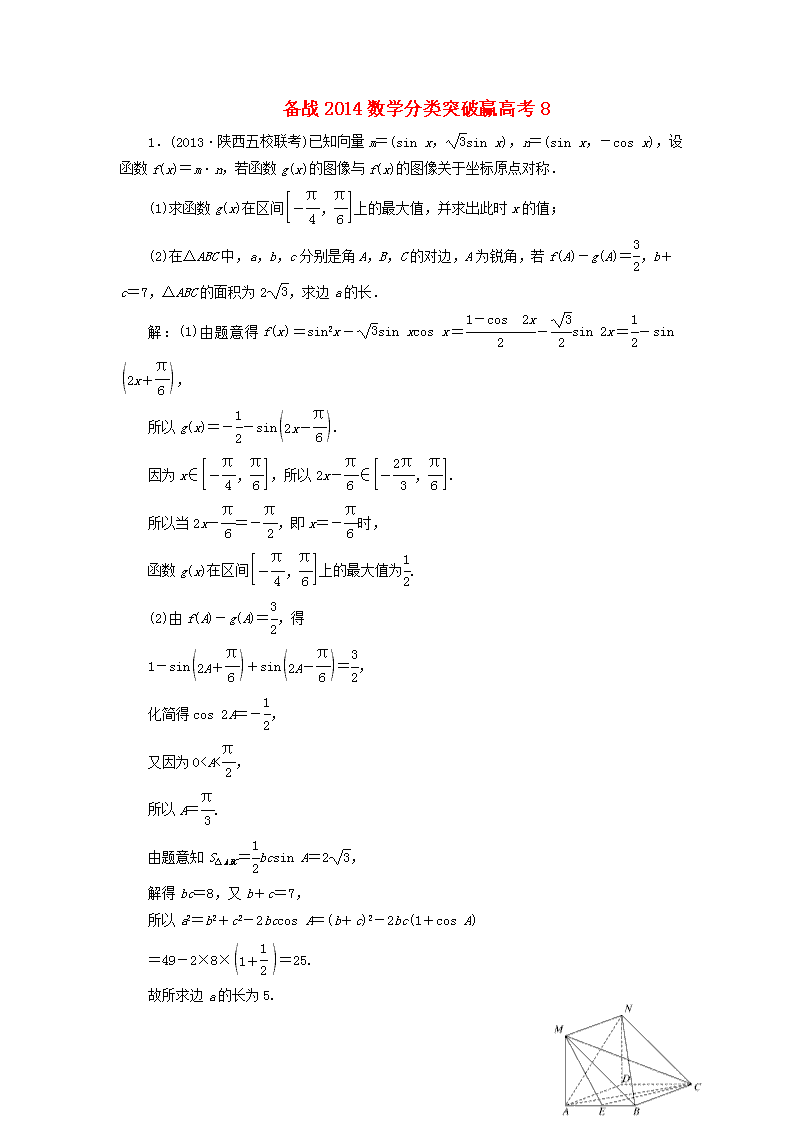


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2014年版高考数学理二轮分类练习题目8
备战2014数学分类突破赢高考8 1.(2013·陕西五校联考)已知向量m=(sin x,sin x),n=(sin x,-cos x),设函数f(x)=m·n,若函数g(x)的图像与f(x)的图像关于坐标原点对称. (1)求函数g(x)在区间上的最大值,并求出此时x的值; (2)在△ABC中,a,b,c分别是角A,B,C的对边,A为锐角,若f(A)-g(A)=,b+c=7,△ABC的面积为2,求边a的长. 解:(1)由题意得f(x)=sin2x-sin xcos x=-sin 2x=-sin, 所以g(x)=--sin. 因为x∈,所以2x-∈. 所以当2x-=-,即x=-时, 函数g(x)在区间上的最大值为. (2)由f(A)-g(A)=,得 1-sin+sin=, 化简得cos 2A=-, 又因为0查看更多
相关文章
- 当前文档收益归属上传用户