- 2021-05-13 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考模拟数学试题理
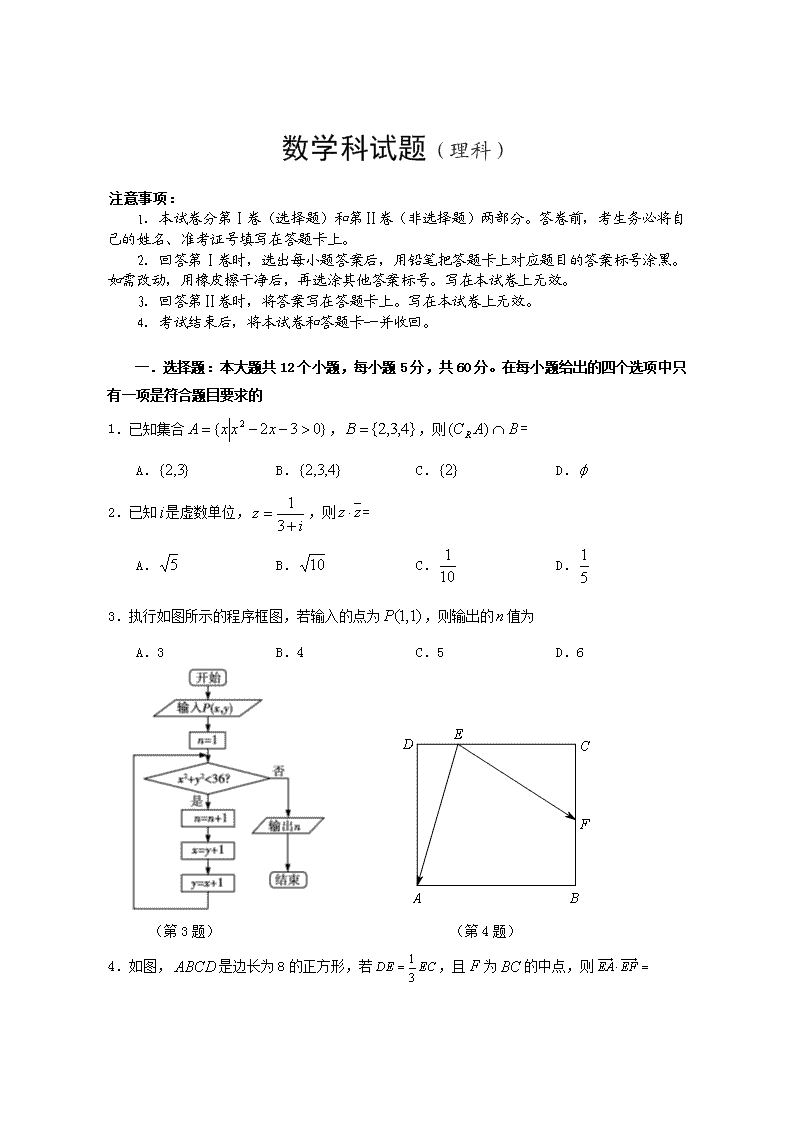
数学科试题(理科) 注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。 3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。 4.考试结束后,将本试卷和答题卡一并收回。 一.选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中只有一项是符合题目要求的 1.已知集合,,则= A. B. C. D. 2.已知是虚数单位,,则= A. B. C. D. 3.执行如图所示的程序框图,若输入的点为,则输出的值为 A.3 B.4 C.5 D.6 (第3题) (第4题) 4.如图,是边长为8的正方形,若,且为的中点,则 A.10 B.12 C.16 D.20 5.若实数满足,则的最大值是 A.4 B.8 C.16 D.32 6.一个棱锥的三视图如右图,则该棱锥的表面积为 A. B. C. D. 7. 5张卡片上分别写有0,1,2,3,4,若从这5张卡片中随机取出2张,则取出的2张卡片上的数字之和大于5的概率是 A. B. C. D. 8.设是数列的前项和,且,,则= A. B. C. D. 9. 函数的大致图像为 10. 底面为矩形的四棱锥的体积为8,若平面,且,则四棱锥的外接球体积最小值是 A. B. C. D. 11. 已知抛物线,过焦点且倾斜角为30°的直线交抛物线于A,B两点,以AB为直径的圆与抛物线的准线相切,切点的纵坐标是3,则抛物线的准线方程为 A. B. C. D. 12. 已知函数(),函数,直线分别与两函数交于两点,则的最小值为 A. B. C. D. 二.填空题:本大题共4小题,每小题5分,共20分. 13. 设样本数据,,...,的方差是5,若(),则,,...,的方差是________ 14. 已知函数(),若,则方程在的实数根个数是_____ 15. 我国的《洛书》中记载着世界上最古老的一个幻方:将1,2,...,9填入 的方格内,使三行、三列、两对角线的三个数之和都等于15 (如图).一般地,将连续的正整数1,2,3,…, 填入的方格内,使得每行、每列、每条对角线上的数的和相等,这个正方形就叫做阶幻方.记阶幻方的一条对角线上数的和为 (如:在3阶幻方中, ),则=_______ 16.已知中,内角A,B,C所对的边分别为,,,且,. 若,则的面积为 三、解答题:本大题共6小题,其中17-21小题为必考题,每小题12分,第22—23题为选考题,考生根据要求做答,每题10分. 17.(本小题满分12分) 设数列是公差为的等差数列. (Ⅰ) 推导数列的通项公式; (Ⅱ) 设,证明数列不是等比数列. 18.(本小题满分12分) 某中学为了解全校学生的上网情况,在全校随机抽取了40名学生(其中男、女生各占一半)进行问卷调查,并进行了统计,按男、女分为两组,再将每组学生的月上网次数分为5组:[0,5),[5,10),[10,15),[15,20),[20,25],得到如图所示的频率分布直方图. (Ⅰ)写出女生组频率分布直方图中的值; (Ⅱ)在抽取的40名学生中从月上网次数不少于20的学生中随机抽取2人,并用表示随机抽取的2人中男生的人数,求的分布列和数学期望. 19.(本小题满分12分) 在直三棱柱中,,。 (Ⅰ)证明:; (Ⅱ) 求直线与平面所成的角. 20.(本小题满分12分) 在平面直角坐标系中,已知椭圆, 圆,若圆的一条切线与椭圆相交于两点. (Ⅰ)当,若点都在坐标轴的正半轴上,求椭圆的方程; (Ⅱ)若以为直径的圆经过坐标原点,探究之间的等量关系. 21.(本小题满分12分) 已知函数(是自然对数的底数). (Ⅰ) 求的单调区间; (Ⅱ)若,当对任意恒成 立时,的最大值为1,求实数的取值范围. 请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分,做答时请先将对应题号用铅笔涂黑. 22.(本小题满分10分)选修4—4:坐标系与参数方程 在直角坐标系中,曲线的参数方程为(为参数).以坐标原点为极点,轴正半轴为极轴,建立极坐标系,曲线的极坐标方程为. (Ⅰ) 写出的普通方程和的直角坐标方程; (Ⅱ) 设点在上,点在上,判断与的位置关系并求的最小值. 23.(本小题满分10分)选修4—5:不等式选讲 已知函数(). (Ⅰ)当时,解不等式; (Ⅱ)当时,不等式恒成立,求实数的取值范围. 数学科答案(理科) 一、 选择题 1-5 6-10 11-12 二、 填空题 13.45 14.3 15.65 16. 一、 解答题 17. 解:(1)因为是等差数列且公差为d,所以...........1 , ,… , .........3 将上述式子相加,得 所以,数列的通项公式为.................6 (2) 假设数列是等比数列,...................................7 当时,,,成等比数列 所以.......................................9 所以 所以,所以,这与矛盾 所以,数列不是等比数列........................12 18.解:(1)由频率分布直方图,得a=错误!未找到引用源。=0.05.........3 (2)在抽取的女生中,月上网次数不少于20的学生的频率为0.02×5=0.1, 学生人数为0.1×20=2..........................4 同理,在抽取的男生中,月上网次数不少于20的 学生人数为0.03×5×20=3,.....................................5 故X的所有可能取值为0,1,2, 则 错误!未找到引用源。,错误!未找到引用源。,...........9 所以X的分布列为 X 0 1 2 P 所以E(X)=0×错误!未找到引用源。+1×错误!未找到引用源。+2×=错误!未找到引用源。..................12 19.解:(1)由题意,以A为坐标原点,以AB,AC,所在直线分别为x轴,y轴,z轴建立空间直角坐标系A-xyz. 因为 则,,,,,......3 所以, 所以..........................................4 所以,所以........................................................5 (2)又因为,所以 所以又因为 所以,............................................8 又,所以.................10 所以 ,............................................11 所以直线与平面所成的角为..............................12 20.解(1)因为圆的一条切线为 所以,当,所以..................2 又点都在坐标轴的正半轴上,所以,所以切线 所以两点坐标是和,..............................4 所以椭圆的方程为........................................5 (2)设,,以为直径的圆经过坐标原 所以,所以..................6 所以 由所以 所以,...............................8 所以.................10 且 所以,................................11 所以...................................................12 21. 解(1)因为............................................1 ①时,恒成立,所以在上单调递增,无减区间;........2 ②时,有, 且时,.时,, 所以的增区间是,减区间是......................4 (2)对任意恒成立, 所以对任意恒成立 所以对任意恒成立..............5 设,因为的最大值为1,.........6 所以 ,.............................................7 令 所以有,且,,, 所以 所以在是单调递增的。...................................10 所以恒成立,所以............................11 所以实数的取值范围是.......................................12 22.解:(Ⅰ) 的普通方程为: ………………(2分) 将的极坐标方程变形为:, ∵,, ∴的直角坐标方程为: 即. ………………(5分) (Ⅱ) 由(Ⅰ)知:曲线与都是圆. 圆的圆心为,半径为;圆的圆心为,半径为 ∵ ∴圆与圆内含 ………………(8分) 的最小值为: ………………(10分) 23.解:(1)由题知,. ......................1 所以①,解得...........................2 ②,解得..........................3 ③,解得.......................4 所以,不等式的解集是..................5 (2)因为,所以................................6 不等式 所以...............................8 所以 所以...................................9 所以 所以,实数m的取值范围是.....................10 工程部维修工的岗位职责 1、 严格遵守公司员工守则和各项规章制度,服从领班安排,除完成日常维修任务外,有计划地承担其它工作任务; 2、 努力学习技术,熟练掌握现有电气设备的原理及实际操作与维修; 3、 积极协调配电工的工作,出现事故时无条件地迅速返回机房,听从领班的指挥; 4、 招待执行所管辖设备的检修计划,按时按质按量地完成,并填好记录表格; 5、 严格执行设备管理制度,做好日夜班的交接班工作; 6、 交班时发生故障,上一班必须协同下一班排队故障后才能下班,配电设备发生事故时不得离岗; 7、 请假、补休需在一天前报告领班,并由领班安排合适的替班人.查看更多