- 2021-05-13 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考之立体几何大题强化训练文科
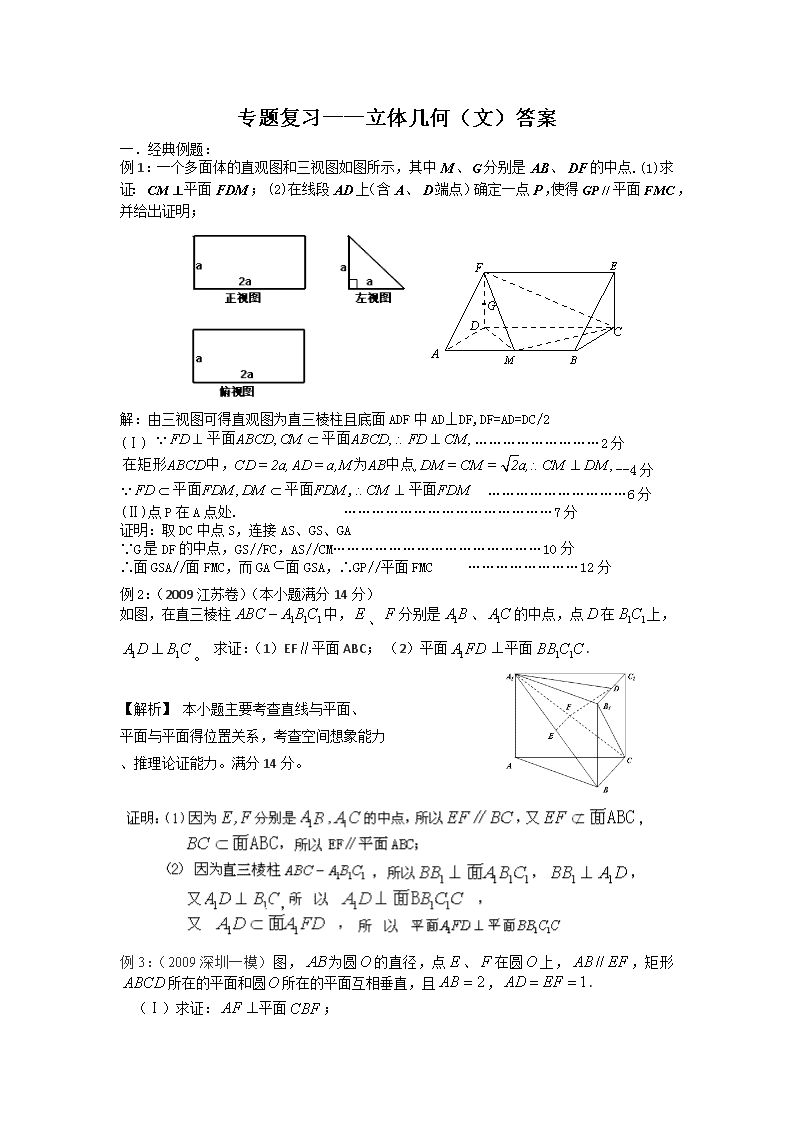
专题复习——立体几何(文)答案 一.经典例题: 例1:一个多面体的直观图和三视图如图所示,其中、分别是、的中点. (1)求证:平面; (2)在线段上(含、端点)确定一点,使得平面,并给出证明; 解:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC/2 (Ⅰ) ………………………2分 --4分 …………………………6分 (Ⅱ)点P在A点处. ………………………………………7分 证明:取DC中点S,连接AS、GS、GA ∵G是DF的中点,GS//FC,AS//CM………………………………………10分 ∴面GSA//面FMC,而GA面GSA,∴GP//平面FMC ……………………12分 例2:(2009江苏卷)(本小题满分14分) 如图,在直三棱柱中,、分别是、的中点,点在上,。 求证:(1)EF∥平面ABC; (2)平面平面. 【解析】 本小题主要考查直线与平面、 平面与平面得位置关系,考查空间想象能力 、推理论证能力。满分14分。 例3:(2009深圳一模)图,为圆的直径,点、在圆上,,矩形所在的平面和圆所在的平面互相垂直,且,. (Ⅰ)求证:平面; (Ⅱ)设的中点为,求证:平面; (Ⅲ) 设平面将几何体分成的两个锥体的体积分别为,,求. (Ⅰ)证明: 平面平面,, 平面平面=, 平面, 平面, ,……… 2分 又为圆的直径,, …………………… 4分 平面。 …………………… 5分 (Ⅱ)设的中点为,则,又, 则,为平行四边形, …………………… 8分 ,又平面,平面, 平面。 …………………… 10分 (Ⅲ)过点作于,平面平面, 平面,, …………………… 12分 平面, ,………………… 13分 . 14分 二.巩固练习: 1.80cm2. 2.答案A. 3.正确的命题有②和③,选C 4.一个四棱锥的直观图和三视图如下图所示,E为PD中点.科网 (I)求证:PB//平面AEC;(II)求四棱锥的体积;(Ⅲ)若F为侧棱PA上一点,且,则为何值时,平面BDF. 解:(1)由三视图得,四棱锥底面ABCD为菱形, 棱锥的高为3,设,则即是棱锥 的高,底面边长是2,连接,分别 是的中点,∥, ∥ (2) (3)过作----10分 ---------------12分 ---------------14分 5.如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,是的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示. (1)求出该几何体的体积; (2)求证:EM∥平面ABC; (3)试问在棱DC上是否存在点N,使NM⊥平面? 若存在,确定点N的位置; 若不存在,请说明理由. (1)∵EA⊥平面ABC,∴EA⊥AB, 又AB⊥AC, ∴AB⊥平面ACDE , 2分 ∴四棱锥B-ACDE的高h=AB=2,梯形ACDE的面积S= 6 ∴, 即所求几何体的体积为4…4分 (2)证明:∵M为DB的中点,取BC中点G,连接EM,MG,AG, ∥ = ∴ MG∥DC,且 ∴ MG AE,∴四边形AGME为平行四边形, 6分 ∴EM∥AG, 又AG平面ABC ∴EM∥平面ABC.……8分 (3)由(2)知,EM∥AG, 又∵平面BCD⊥底面ABC,AG⊥BC,∴AG⊥平面BCD ∴EM⊥平面BCD,又∵EM平面BDE, ∴平面BDE⊥平面BCD 10分 在平面BCD中,过M作MN⊥DB交DC于点N, ∴MN⊥平面BDE 点N即为所求的点 11分 ∵∽ 13分 ∴ 边DC上存在点N,满足DN=DC时,有NM⊥平面BDE. 14分 6.(2009福建卷文)(本小题满分12分)如图,平行四边形中,,将沿折起到的位置,使平面平面 (I)求证: (Ⅱ)求三棱锥的侧面积。 (I)证明:在中, 又平面平面 平面平面平面 平面 平面 (Ⅱ)解:由(I)知从而 在中, 又平面平面 平面平面,平面 而平面 综上,三棱锥的侧面积,查看更多