2017年度高考物理专题二（第1讲直线运动及其规律）二轮强化训练

2017年度高考物理专题二（第1讲直线运动及其规律）二轮强化训练

‎【走向高考】2014年高考物理二轮专题复习 专题二 第1讲 直线运动及其规律课后强化作业 ‎1．某人用手表估测火车的加速度，先观测2分钟，发现火车前进‎480米，隔2分钟后，又观测1分钟，发现火车前进‎618米，若火车在这5分钟内做匀加速直线运动，则火车的加速度为(　　)‎ A．‎0.03m/s2　　　　　　　 B．‎0.01m/s2‎ C．‎0.5m/s2 D．‎0.6m/s2‎ ‎[答案]　A ‎[解析]　前2分钟的平均速度v1＝m/s＝‎4m/s，最后1分钟内的平均速度为v2＝m/s＝‎10.3m/s，火车的加速度为a＝＝m/s2＝‎0.03m/s2。‎ ‎2．某汽车在一笔直公路上运动，在t时间内通过的位移为x，若它在中间位置处的速度为v1，在中间时刻t时的速度为v2，则v1和v2的关系为(　　)‎ A．当汽车做匀加速直线运动时，v1>v2‎ B．当汽车做匀减速直线运动时，v1>v2‎ C．当汽车做匀速直线运动时，v1＝v2‎ D．当汽车做匀减速直线运动时，v1v2；当v0＝vt时，汽车做匀速直线运动，必有v1＝v2。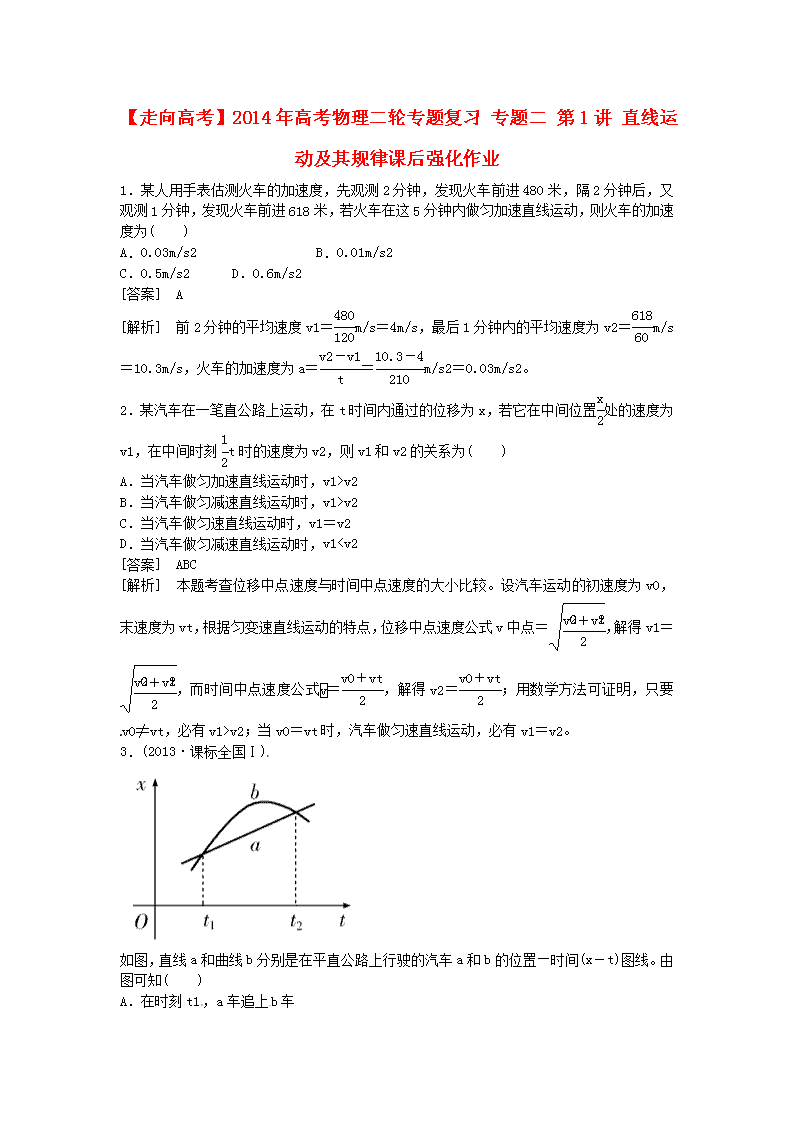‎ ‎3．(2013·课标全国Ⅰ)‎ 如图，直线a和曲线b分别是在平直公路上行驶的汽车a和b的位置—时间(x－t)图线。由图可知(　　)‎ A．在时刻t1，a车追上b车 B．在时刻t2，a、b两车运动方向相反 C．在t1到t2这段时间内，b车的速率先减少后增加 D．在t1到t2这段时间内，b车的速率一直比a车的大 ‎[答案]　BC ‎[解析]　t1时刻，两车都在沿x正方向运动，该时刻前，b车的位置坐标小，b车在a车的后面，所以t1时刻是b追上a，A项错；t2时刻，a车继续沿x正方向运动，而b车向x负方向运动，二者运动方向相反，B项正确；在位移—时间图象中，图线斜率的大小表示速度的大小，t1到t2时间内，b的斜率先减小后增大，故b车的速率先减小后增大，C项正确；t1到t2时间内，曲线b的斜率大小存在比a的斜率大的时间段，也存在比a小的时间段，D项错。‎ ‎4．(2013·上海崇明县检测)某人站在三楼阳台上，同时以‎10m/s的速率抛出两个小球，其中一个小球竖直上抛，另一个球竖直下抛，它们落地的时间差为Δt；如果该人站在六楼阳台上，以同样的方式抛出两个小球，它们落地的时间差为Δt′。不计空气阻力，Δt′和Δt相比较，有(　　)‎ A．Δt′<Δt B．Δt′＝Δt C．Δt′>Δt D．无法判断 ‎[答案]　B ‎[解析]　以竖直向下为正方向，设物体从抛出到落地的位移为h，对于竖直下抛的物体有h＝v0t＋gt2，对于竖直上抛的物体有h＝－v0t＋gt2，由以上两式得Δt＝t2－t1＝，时间差与高度无关，故B正确。‎ ‎5．(2013·上海普陀区检测)关于自由落体运动，下列说法中正确的是(　　)‎ A．在连续相等的位移内所用时间相等 B．在连续相等的位移内平均速度相等 C．在任何相等的时间内速度的变化量相等 D．在任何相等的时间内位移的变化相等 ‎[答案]　C ‎[解析]　自由落体运动是初速度为零的匀加速直线运动，速度的变化量Δv＝gΔt，在任何相等的时间内速度的变化量相等，C正确，自由落体运动在连续相等的位移内所用时间t1t2t3……＝1(－1)(－)……，A错误；自由落体运动在连续相等的位移内所用时间不同，故在连续相等的位移内平均速度不相等，B错误，自由落体运动在连续相等的时间内位移大小之比x1x2x3……＝135……，故在任何相等的时间内位移的变化不相等，D错误。‎ ‎6.‎ ‎(2013·黑龙江哈九中检测)甲、乙两物体在同一直线上运动的x－t图象如图所示，以甲的出发点为原点，出发时刻为计时起点，则从图象可以看出(　　)‎ A．t2到t3这段时间内甲的平均速度大于乙的平均速度 B．乙比甲先出发 C．甲开始运动时，乙在甲前面x0处 D．甲在中途停了一会儿，最终也没追上乙 ‎[答案]　AC ‎[解析]　从图象可知，t2到t3这段时间内甲的位移大于乙的位移，故甲的平均速度大于乙的平均速度，A正确；乙和甲同时出发，B错误；甲从坐标原点处出发，乙从离坐标原点x0处出发，C正确；甲在中途停了一会儿，最终在t3时刻追上乙，D错误。‎ ‎7．(2013·安徽黄山质量检测)一个做匀加速直线运动的物体的加速度是‎3m/s2，这意味着(　　)‎ A．该物体在任1s末的速度是该秒初速度的3倍 B．该物体在任1s末的速度比该秒的初速度大‎3m/s C．该物体在第1s末的速度为‎3m/s D．该物体在任1s初的速度比前1s末的速度大‎3m/s ‎[答案]　B ‎[解析]　根据vt＝v0＋at得，该物体在任1s末的速度比该秒的初速度大‎3m/s，A错误，B正确；该物体在第1s末的速度v1＝v0＋‎3m/s，因不知初速度，故C错误；该物体在任1s初的速度与前1s末的速度相等，故D错误。‎ ‎8．(2013·河南郑州第一次质检)做匀加速直线运动的质点在第一个7s内的平均速度比它在第一个3s内的平均速度大‎6m/s，则质点的加速度大小为(　　)‎ A．‎1m/s2 B．‎1.5m/s2‎ C．‎3m/s2 D．‎4m/s2‎ ‎[答案]　C ‎[解析]　做匀加速直线运动的质点在第一个3s内的平均速度等于质点在1.5s末的瞬时速度，设为v1，在第一个7s内的平均速度等于质点在3.5s末的瞬时速度，设为v2，则v2＝v1＋‎6m/s，根据加速度的定义得a＝＝＝‎3m/s2，故C正确。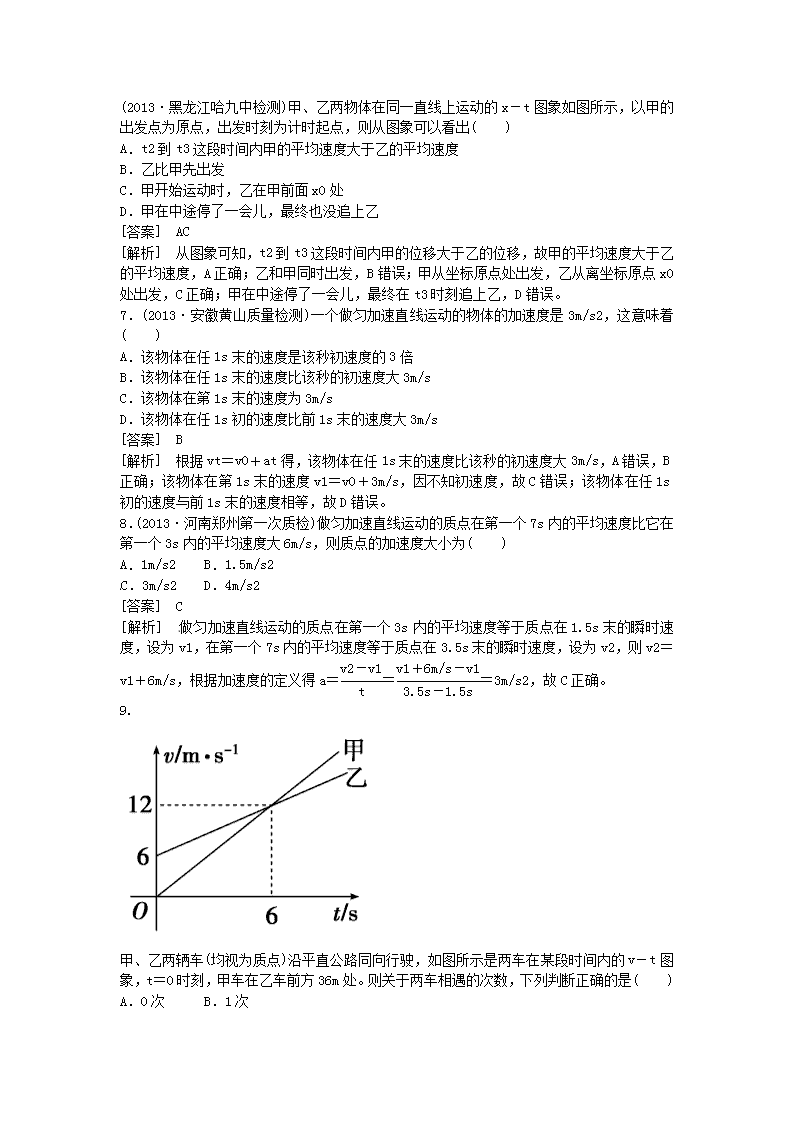‎ ‎9.‎ 甲、乙两辆车(均视为质点)沿平直公路同向行驶，如图所示是两车在某段时间内的v－t图象，t＝0时刻，甲车在乙车前方‎36m处。则关于两车相遇的次数，下列判断正确的是(　　)‎ A．0次 B．1次 C．2次 D．条件不足，无法判断 ‎[答案]　A ‎[解析]　由图可知，两车速度相等时，甲车的位移x1＝‎36m，乙车的位移x2＝‎54m，甲、乙两车的位移差为x＝x2－x1＝‎18m<‎36m，此时两车不可能相遇，之后乙车的速度小于甲车，两车不会相遇，故选项A正确。‎ ‎10．一个从地面竖直上抛的物体，它两次经过一个较低的点a的时间间隔是Ta，两次经过一个较高点b的时间间隔是Tb，则a、b之间的距离为(　　)‎ A.g(T－T) B.g(T－T)‎ C.g(T－T) D.g(Ta－Tb)‎ ‎[答案]　A ‎[解析]　根据时间的对称性，物体从a点到最高点的时间为，从b点到最高点的时间为，所以a点到最高点的距离ha＝g()2＝，b点到最高点的距离hb＝g()2＝，故a、b之间的距离为ha－hb＝g(T－T) ，即选A。‎ ‎11．(2013·四川成都第二次诊断性考试)‎ 潜艇部队经常开展鱼雷攻击敌方舰艇演练。某次演习的简化模型为：敌舰沿直线MN匀速航行，潜艇隐蔽在Q点不动，Q到的距离＝‎2000m。当敌舰到达距离O点‎800m的A点时，潜艇沿QO方向发射一枚鱼雷，正好在O点击中敌舰。敌舰因受鱼雷攻击，速度突然减为原来的，且立刻沿原运动方向做匀加速运动逃逸。100s后潜艇沿QB方向发射第二枚鱼雷，鱼雷在B点再次击中敌舰。测得＝‎1500m，不考虑海水速度的影响，潜艇和敌舰可视为质点，鱼雷的速度大小恒为‎25m/s。求：‎ ‎(1)敌舰第一次被击中前的速度；‎ ‎(2)鱼雷由Q至B经历的时间；‎ ‎(3)敌舰逃逸时的加速度大小(可用分式表示结果)。‎ ‎[答案]　(1)‎10m/s　(2)100s　(3)‎0.025m/s2‎ ‎[解析]　(1)鱼雷从Q到O经历的时间t1＝＝m/s＝80s 敌舰被击中前的速度v1＝＝m/s＝‎10m/s ‎(2)设第二枚鱼雷经过时间t2击中敌舰，则 ＝＝m＝‎‎2500m t2＝＝s＝100s ‎(3)敌舰第一次被击中后瞬间的速度v2＝＝＝‎5m/s 敌舰被第一次击中后运动的时间t3＝t2＋100s＝200s 设敌舰的加速度为a，由＝v2t3＋at 得a＝ 代入数据得a＝m/s2＝m/s2＝‎0.025m/s2‎ ‎12.‎ ‎(2013·四川新津中学一模)如图所示，隧道是高速公路上的特殊路段也是事故多发路段之一。某日，一辆轿车A因故恰停在隧道内离隧道入口d＝‎50m的位置。此时另一辆轿车B正以v0＝‎90km/h的速度匀速向隧道口驶来，轿车B的驾驶员在进入隧道口时，才发现停在前方的轿车A并立即采取制动措施。假设该驾驶员反应时间t1＝0.57s，轿车制动系统响应时间(开始踏下制动踏板到实际制动)t2＝0.03s，轿车制动时制动力恒为自身重力的0.75倍，g取‎10m/s2。‎ ‎(1)试通过计算说明该轿车B会不会与停在前面的轿车A相撞？‎ ‎(2)若会相撞，那么撞前瞬间轿车B速度大小为多少？若不会相撞，那么停止时与轿车A的距离为多少？‎ ‎[答案]　(1)会相撞　(2)‎10m/s ‎[解析]　(1)轿车实际制动前的0.6s内做匀速直线运动，匀速运动的位移为x1＝×‎0.6m＝‎15m，实际制动中的加速度大小a＝‎0.75g＝‎7.5m/s2，实际制动中当速度减为零时的位移x2＝＝m＝m，由于x1＋x2＝m＝‎56.7m>‎50m，故B会与停在前面的轿车A相撞。‎ ‎(2)设与A相碰时的速度为v，根据运动学公式得：－2×7.5×(50－15)m＝v2－2，解得v＝‎10m/s。‎ ‎13. 跳伞运动员做低空跳伞表演，离地面‎224m离开飞机在竖直方向做自由落体运动，运动一段时间后，立即打开降落伞，展伞后运动员以‎12.5m/s2的平均加速度匀减速下降，为了运动员的安全，要求运动员落地速度最大不得超过‎5m/s(g＝‎10m/s2)。求：‎ ‎(1)运动员展伞时，离地面的高度至少为多少？‎ ‎(2)运动员以最大速度落地时相当于从多高处自由落下？‎ ‎(3)运动员在空中的最短时间为多少？‎ ‎[答案]　(1)‎99m　(2)‎1.75m　(3)8.6s ‎ [解析]　‎ 运动员在竖直方向上的运动情况如图所示。‎ ‎(1)由公式v－v＝2as可得 第一阶段：v2＝2gh1‎ 第二阶段：v2－v＝2ah2‎ 又h1＋h2＝H 解以上三式可得展伞时离地面的高度至少为h2＝‎‎99m ‎(2)设以‎5m/s的速度着地相当于从高h′处自由下落，则h′＝＝‎‎1.25m ‎(3)由公式s＝v0t＋at2可得 第一阶段：h1＝gt 第二阶段：v＝gt1，v－vm＝at2‎ 又t＝t1＋t2‎ 解上述三式可得运动员在空中的最短时间为t＝8.6s。‎ ‎14．(2013·课标全国Ⅰ)水平桌面上有两个玩具车A和B，两者用一轻质细橡皮筋相连，在橡皮筋上有一红色标记R。在初始时橡皮筋处于拉直状态，A、B和R分别位于直角坐标系中的(0,‎2l)、(0，－l)和(0,0)点。已知A从静止开始沿y轴正向做加速度大小为a的匀加速运动；B平行于x轴朝x轴正向匀速运动。在两车此后运动的过程中，标记R在某时刻通过点(l，l)。假定橡皮筋的伸长是均匀的，求B运动速度的大小 ‎ [答案]　 ‎[解析]　‎ 设B车的速度大小为v。如图，标记R在时刻t通过K(l，l)，此时A、B的位置分别为H、G。由运动学公式，H的纵坐标yA，G的横坐标xB分别为 yA＝‎2l＋at2①‎ xB＝vt②‎ 在开始运动时，R到A和B的距离之比为21，即 OEOF＝21‎ 由于橡皮筋的伸长是均匀的，在以后任一时刻R到A和B的距离之比都为21。因此，在时刻t有 HKKG＝21③‎ 由于△FGH∽△IGK，有 HGKG＝xB(xB－l)④‎ HGKG＝(yA＋l)(‎2l)⑤‎ 由③④⑤式得 xB＝l⑥‎ yA＝‎5l⑦‎ 联立①②⑥⑦式得 v＝⑧‎