专题 立体几何高考数学理试题分项解析原卷

专题 立体几何高考数学理试题分项解析原卷

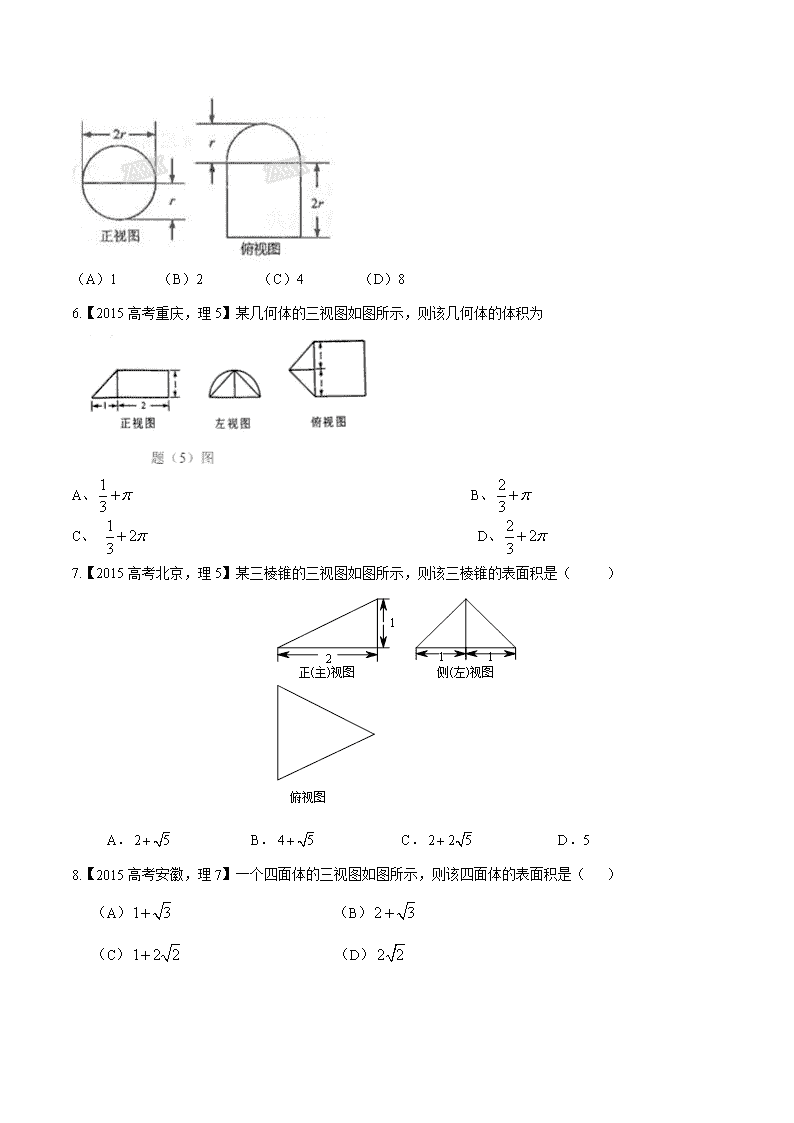
第十章 立体几何 ‎1.【2015高考安徽，理5】已知，是两条不同直线，，是两个不同平面，则下列命题正确的是（ ）‎ ‎ （A）若，垂直于同一平面，则与平行 ‎ （B）若，平行于同一平面，则与平行 ‎ （C）若，不平行，则在内不存在与平行的直线 ‎ （D）若，不平行，则与不可能垂直于同一平面 ‎2.【2015高考北京，理4】设，是两个不同的平面，是直线且．“”是“”的（ ）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件[来源:学科网]‎ ‎3.【2015高考新课标1，理6】《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题:“今有委米依垣内角，下周八尺，高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图，米堆为一个圆锥的四分之一)，米堆为一个圆锥的四分之一)，米堆底部的弧长为8尺，米堆的高为5尺，问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺，圆周率约为3，估算出堆放斛的米约有（ ）‎ ‎(A)14斛 (B)22斛 (C)36斛 (D)66斛 ‎4.【2015高考陕西，理5】一个几何体的三视图如图所示，则该几何体的表面积为（ ）‎ A． B． C． D．‎ ‎5.【2015高考新课标1，理11】圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20，则r=（ ）‎ ‎（A）1 （B）2 （C）4 （D）8‎ ‎6.【2015高考重庆，理5】某几何体的三视图如图所示，则该几何体的体积为 A、 B、‎ C、 D、‎ ‎7.【2015高考北京，理5】某三棱锥的三视图如图所示，则该三棱锥的表面积是（ ）‎ A． B． C． D．5‎ ‎8.【2015高考安徽，理7】一个四面体的三视图如图所示，则该四面体的表面积是（ ）‎ ‎ （A） （B）‎ ‎ （C） （D）‎ ‎ ‎ ‎9.【2015高考新课标2，理9】已知A,B是球O的球面上两点，∠AOB=90,C为该球面上的动点，若三棱锥 O-ABC体积的最大值为36，则球O的表面积为( )‎ A．36π B.64π C.144π D.256π ‎10.【2015高考山东，理7】在梯形中，， .将梯 形绕所在的直线旋转一周而形成的曲面所围成的几何体的体积为（ ）‎ ‎（A） （B） （C） （D） ‎ ‎11.【2015高考浙江，理8】如图，已知，是的中点，沿直线将折成，所成二面角的平面角为，则（ ）‎ A. B. C. D. ‎ ‎12.【2015高考浙江，理2】某几何体的三视图如图所示（单位：cm），则该几何体的体积是（ ）‎ ‎ A. B. C. D. ‎ ‎13.【2015高考福建，理7】若 是两条不同的直线， 垂直于平面 ，则“ ”是“ 的 （ ） ‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎14.【2015高考新课标2，理6】一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为( )‎ A． B． C． D．‎ ‎15.【2015高考四川，理14】如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为，则的最大值为 .‎ ‎16.【2015高考天津，理10】一个几何体的三视图如图所示（单位：），则该几何体的体积为 ‎ . ‎ ‎17.【2015高考浙江，理13】如图，三棱锥中，，点分别是的中点，则异面直线，所成的角的余弦值是 ．‎ ‎18.【2015江苏高考，9】现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2、高为8的圆柱各一个。若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥与圆柱各一个，则新的底面半径为 ‎ ‎19.【2015高考新课标2，理19】（本题满分12分）‎ 如图，长方体中,，，，点，分别在，上，．过点，的平面与此长方体的面相交，交线围成一个正方形．‎ D D1‎ C1‎ A1‎ E F A B C B1‎ ‎（Ⅰ）在图中画出这个正方形（不必说出画法和理由）；‎ ‎（Ⅱ）求直线与平面所成角的正弦值．‎ ‎20.【2015江苏高考，16】（本题满分14分）[来源:Zxxk.Com]‎ 如图，在直三棱柱中，已知，，设的中点为，.求证：（1）；‎ ‎ （2）.‎ A B C D E A1‎ B1‎ C1‎ ‎21.【2015高考安徽，理19】如图所示，在多面体，四边形，均为正方形，为的中点，过的平面交于F.‎ ‎ （Ⅰ）证明：；‎ ‎ （Ⅱ）求二面角余弦值.‎ ‎22.【2015江苏高考，】（本小题满分10分）‎ 如图，在四棱锥中，已知平面，且四边形为直角梯 ‎ 形，,‎ ‎ （1）求平面与平面所成二面角的余弦值；[来源:学|科|网]‎ ‎ （2）点Q是线段BP上的动点，当直线CQ与DP所成角最小时，求线段BQ的长 P A B C D Q ‎23.【2015高考福建，理17】如图，在几何体ABCDE中，四边形ABCD是矩形，AB平面BEC，BEEC，AB=BE=EC=2，G，F分别是线段BE，DC的中点.‎ ‎(Ⅰ)求证：平面 ； ‎ ‎(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值．‎ ‎24.【2015高考浙江，理17】如图，在三棱柱-中，，，，在底面的射影为的中点，为的中点.‎ ‎（1）证明：D平面；‎ ‎（2）求二面角-BD-的平面角的余弦值.‎ ‎25.【2015高考山东，理17】如图，在三棱台中，分别为的中点.‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）若平面， ， ,求平面与平面 所成的角（锐角）的大小.‎ ‎26.【2015高考天津，理17】（本小题满分13分）如图，在四棱柱中，侧棱,,,‎ ‎,且点M和N分别为的中点.‎ ‎(I)求证：平面；‎ ‎(II)求二面角的正弦值；‎ ‎(III)设为棱上的点，若直线和平面所成角的正弦值为，求线段的长 ‎27.【2015高考重庆，理19】如题（19）图，三棱锥中，平面分别为线段上的点，且 ‎ （1）证明：平面 ‎ （2）求二面角的余弦值。‎ ‎28.【2015高考四川，理18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示，在正方体中，设的中点为，的中点为 ‎（1）请将字母标记在正方体相应的顶点处（不需说明理由）‎ ‎（2）证明：直线平面 ‎（3）求二面角的余弦值.‎ ‎29.【2015高考湖北，理19】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马中，侧棱底面，且，过棱的中点，作交于点，连接 ‎ ‎（Ⅰ）证明：．试判断四面体是否为鳖臑，若是，写出其每个面的直角（只需写 出结论）；若不是，说明理由；[来源:学科网]‎ ‎（Ⅱ）若面与面所成二面角的大小为，求的值．‎ ‎30.【2015高考陕西，理18】（本小题满分12分）如图，在直角梯形中，，，，，是的中点，是与的交点．将沿折起到的位置，如图．‎ ‎ ‎ ‎（I）证明：平面；‎ ‎（II）若平面平面，求平面与平面夹角的余弦值．‎ ‎31.【2015高考新课标1，理18】如图，，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.‎ ‎（Ⅰ）证明：平面AEC⊥平面AFC；‎ ‎（Ⅱ）求直线AE与直线CF所成角的余弦值.‎ ‎32.【2015高考北京，理17】如图，在四棱锥中，为等边三角形，平面平面，，，，，为的中点．‎ ‎(Ⅰ) 求证：；‎ ‎(Ⅱ) 求二面角的余弦值；‎ ‎(Ⅲ) 若平面，求的值．‎ ‎ ‎ ‎33.【2015高考广东，理18】如图2，三角形所在的平面与长方形所在的平面垂直，，，.点是边的中点，点、分别在线段、上，且，．‎ ‎（1）证明：；‎ ‎（2）求二面角的正切值；‎ ‎（3）求直线与直线所成角的余弦值．‎图2‎ P A B C D E F G ‎ [来源