近四年20052008上海高考立体几何试题

近四年20052008上海高考立体几何试题

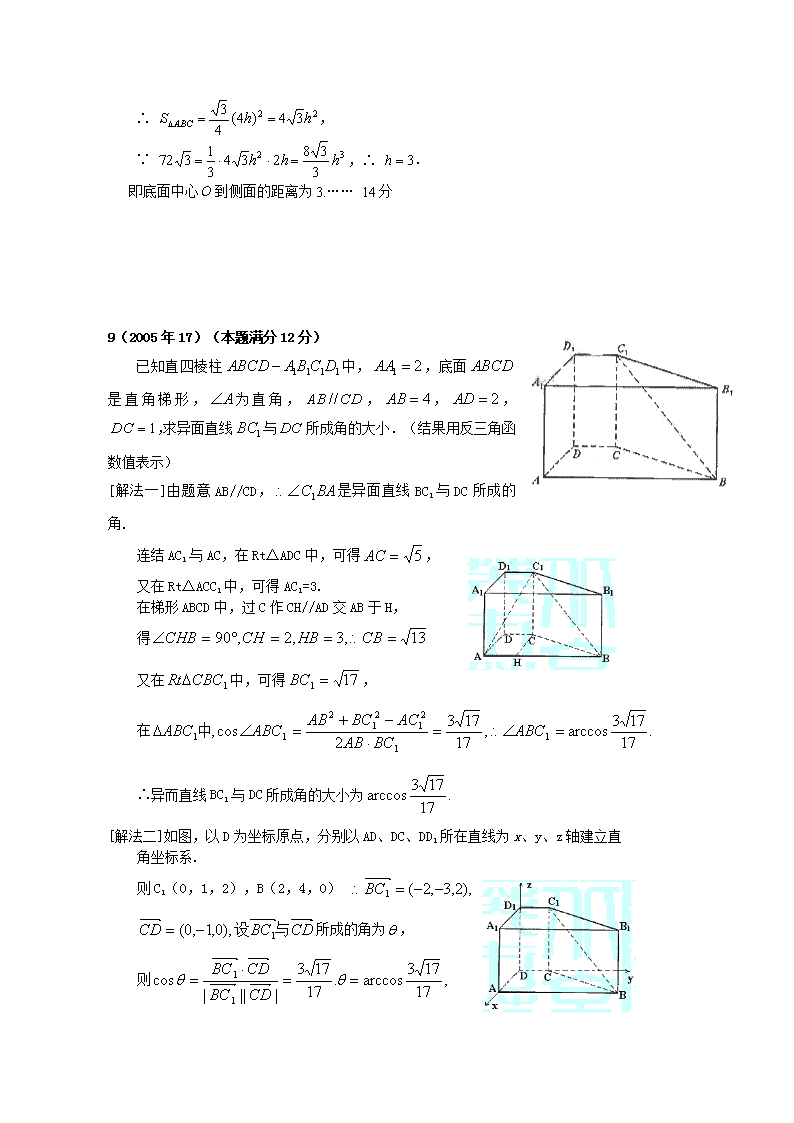
近四年（2005-2008）上海高考立体几何试题 ‎ 一．填空题：只要求直接填写结果 ‎1（2005年11）有两个相同的直三棱柱，高为，底面三角形的三边长分别为。用它们拼成一个三棱柱或四棱柱，在所有可能的情形中，表面积最小的是一个四棱柱，则的取值范围是__________。‎ 解答：两个相同的直三棱柱并排放拼成一个三棱柱或四棱柱，有三种情况 四棱柱有一种，就是边长为的边重合在一起，表面积为24+28‎ 三棱柱有两种，边长为的边重合在一起，表面积为24+32边长为的边重合在一起，表面积为24+36 ‎ 两个相同的直三棱柱竖直放在一起，有一种情况表面积为12+48‎ 最小的是一个四棱柱，这说明 ‎2（2006春8） 正四棱锥底面边长为4，侧棱长为3，则其体积为 . ‎ ‎3（2006年10）如果一条直线与一个平面垂直，则称此直线与平面构成一个“正交线面对”．在一个正方体中，由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 ；‎ 解：正方体中，一个面有四条棱与之垂直，六个面，共构成24个“正交线面对”；而正方 体的六个对角截面中，每个对角面又有两条面对角线与之垂直，共构成12个“正交线面对”，所以共有36个“正交线面对”；‎ ‎4（2007年10）在平面上，两条直线的位置关系有相交、平行、重合三种． 已知是两个 ‎ 相交平面，空间两条直线在上的射影是直线，在上的射影是 直线．用与，与的位置关系，写出一个总能确定与是异 ‎ 面直线的充分条件： ．‎ ‎，并且与相交（，并且与相交）‎ ‎5（2008春8）已知一个凸多面体共有9个面，所有棱长均为1，其平面展开图 ‎ 如右图所示，则该凸多面体的体积 ‎ 二．选择题：每题都给出四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在题后的圆括号内，‎ ‎6（2005春13） 已知直线及平面，下列命题中的假命题是 （ ）‎ ‎ （A）若，，则. （B）若，，则.‎ ‎ （C）若，，则. （D）若，，则.‎ ‎ [答] ( D )‎ ‎7（2006年14）若空间中有四个点，则“这四个点中有三点在同一直线上”是“这四个点在同一平面上”‎ 的 （ ）‎ ‎（A）充分非必要条件；（B）必要非充分条件；（C）充要条件；（D）非充分非必要条件；‎ 解： 充分性成立： “这四个点中有三点在同一直线上”有两种情况：‎ ‎1）第四点在共线三点所在的直线上，可推出“这四个点在同一平面上”；‎ ‎2）第四点不在共线三点所在的直线上，可推出“这四点在唯一的一个平面内”；‎ ‎ 必要性不成立：“四个点在同一平面上”可能推出“两点分别在两条相交或平行直线上”；‎ ‎ 故选（A）‎ 三．解答题：解答下列各题必须写出必要的步骤.‎ ‎8（2005春19） (14分) 本题共有2个小题，第1小题满分6分，第2小题满分8分.‎ 已知正三棱锥的体积为，侧面与底面所成的二面角的大小为.‎ ‎ （1）证明：；‎ ‎ （2）求底面中心到侧面的距离. ‎ ‎ ‎ ‎[证明]（1）（1）取边的中点，连接、，‎ ‎ 则，，故平面. …… 4分 ‎ ∴ . …… 6分 ‎[解]（2）如图， 由（1）可知平面平面，则是侧面与底面所成二面角的平面角.‎ ‎ 过点作为垂足，则就是点到侧面的距离.…… 9分 设为，由题意可知点在上，‎ ‎∴ ，.‎ ‎, …… 11分 ‎ ∴ ，‎ ‎ ∵ ，∴ .‎ ‎ 即底面中心到侧面的距离为3.…… 14分 ‎9（2005年17）（本题满分12分）‎ ‎ 已知直四棱柱中，，底面是直角梯形，为直角，，，，，求异面直线与所成角的大小．（结果用反三角函数值表示）‎ ‎[解法一]由题意AB//CD，是异面直线BC1与DC所成的角.‎ 连结AC1与AC，在Rt△ADC中，可得，‎ 又在Rt△ACC1中，可得AC1=3.‎ 在梯形ABCD中，过C作CH//AD交AB于H，‎ 得 又在中，可得，‎ 在 ‎∴异而直线BC1与DC所成角的大小为 ‎[解法二]如图，以D为坐标原点，分别以AD、DC、DD1所在直线为x、y、z轴建立直 角坐标系.‎ 则C1（0，1，2），B（2，4，0） ‎ 所成的角为，‎ 则 ‎∴异面直线BC1与DC所成角的大小为 ‎10（2006春17） (本题满分12分)在长方体中，已知，求异面直线与所成角的大小（结果用反三角函数值表示）.‎ ‎[解法一] 连接，‎ ‎ 为异面直线与所成的角. ……4分 ‎ 连接，在△中，， ……6分 ‎ 则 ‎ . ……10分 ‎ 异面直线与所成角的大小为.……12分 ‎[解法二] 以为坐标原点，分别以、、所在直线为轴、轴、轴，建立空间直角坐标系. ……2分 ‎ 则 ， ‎ ‎ 得 . ……6分 ‎ 设与的夹角为，‎ ‎ 则， ……10分 ‎ 与的夹角大小为， ‎ ‎ 即异面直线与所成角的大小为. ……12分 ‎11（2006年19）（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分）‎ 在四棱锥P－ABCD中，底面是边长为2的菱形，∠DAB＝60，对角线AC与BD相交 P A B C D O E 于点O，PO⊥平面ABCD，PB与平面ABCD所成的角为60．‎ ‎（1）求四棱锥P－ABCD的体积；‎ ‎（2）若E是PB的中点，求异面直线 DE与PA所成角的大小（结果用 反三角函数值表示）．‎ ‎[解]（1）在四棱锥P-ABCD中,由PO⊥平面ABCD,得 ‎∠PBO是PB与平面ABCD所成的角, ∠PBO=60°.‎ 在Rt△AOB中BO=ABsin30°=1, 由PO⊥BO,‎ 于是,PO=BOtg60°=,而底面菱形的面积为2.‎ ‎∴四棱锥P-ABCD的体积V=×2×=2.‎ ‎（2）解法一：以O为坐标原点,射线OB、OC、‎ OP分别为x轴、y轴、z轴的正半轴建立 空间直角坐标系.‎ 在Rt△AOB中OA=,于是,点A、B、‎ D、P的坐标分别是A(0,－,0),‎ B (1,0,0), D (－1,0,0), P (0,0, ).‎ E是PB的中点,则E(,0,) 于是=(,0, ),=(0, ,).‎ 设的夹角为θ,有cosθ=,θ=arccos,‎ ‎∴异面直线DE与PA所成角的大小是arccos；‎ ‎ 解法二：取AB的中点F,连接EF、DF.‎ 由E是PB的中点,得EF∥PA，‎ ‎∴∠FED是异面直线DE与PA所成 角(或它的补角)，‎ 在Rt△AOB中AO=ABcos30°==OP，‎ 于是, 在等腰Rt△POA中，‎ PA=，则EF=.‎ 在正△ABD和正△PBD中,DE=DF=，‎ ‎ cos∠FED==‎ ‎∴异面直线DE与PA所成角的大小是arccos.‎ ‎12（2007春 16） (12分)如图，在棱长为2的正方体中，分别是和的中点，求异面直线与所成角的大小 (结果用反三角函数值表示）.‎ ‎[解法一] 如图建立空间直角坐标系. …… 2分 由题意可知.‎ ‎ . …… 6分 ‎ 设直线与所成角为，则. ……10分 ‎ ，‎ ‎ 即异面直线与所成角的大小为. …… 12分 ‎[解法二] 连接， …… 2分 ‎ ，且，是平行四边形，则，‎ ‎ 异面直线与所成的角就是与所成的角. …… 6分 ‎ 由平面，得. ‎ ‎ 在△中，，则 ‎ ， …… 10分 ‎ . ‎ ‎ 异面直线与所成角的大小为. …… 12分 ‎13（2007年16）（本题满分12分）如图，在体积为1的直三棱柱中，．求直线与平面所成角的大小（结果用反三角函数值表示）．‎ 解法一： 由题意，可得体积 ‎， ‎ ‎ ． ‎ 连接． ，‎ 平面，‎ ‎ 是直线与平面所成的角． ‎ ‎ ， ‎ ‎ ，则 ＝．‎ ‎ 即直线与平面所成角的大小为． ‎ 解法二： 由题意，可得 ‎ 体积，‎ ‎ ， ‎ ‎ 如图，建立空间直角坐标系． 得点，‎ ‎，． 则，平面的法向量为．‎ ‎ 设直线与平面所成的角为，与的夹角为， ‎ ‎ 则， ，‎ ‎ 即直线与平面所成角的大小为． ‎ ‎14（2008春20）(本题满分14分)本题共有2个小题，第1小题满分6分，第2小题满分8分.‎ ‎ 某厂根据市场需求开发折叠式小凳（如图所示）. 凳面为三角形的尼龙布，凳脚为三根细钢管. 考虑到钢管的受力和人的舒适度等因素，设计小凳应满足：① 凳子高度为，② 三根细钢管相交处的节点与凳面三角形重心的连线垂直于凳面和地面. ‎ ‎（1）若凳面是边长为的正三角形，三只凳脚与地面所成的角均为，确定节点分细钢管上下两段的比值（精确到）；‎ ‎（2）若凳面是顶角为的等腰三角形，腰长为，节点分细钢管上下两段之比为. 确定三根细钢管的长度（精确到）.‎ ‎[解]（1）设△的重心为，连结.‎ 由题意可得，. 设细钢管上下两段之比为. ‎ ‎ 已知凳子高度为. 则. …… 3分 ‎ 节点与凳面三角形重心的连线与地面垂直，且凳面与地面平行.‎ ‎ 就是与平面所成的角，亦即.‎ ‎ ，解得，. …… 6分 ‎ 即节点分细钢管上下两段的比值约为.‎ ‎（2）设，.‎ ‎ 设△的重心为，则， …… 10分 ‎ 由节点分细钢管上下两段之比为，可知. ‎ ‎ 设过点的细钢管分别为，‎ ‎ 则 ，‎ ‎ ， ‎ ‎ 对应于三点的三根细钢管长度分别为， 和. 14分