高考数学文科知识网络

高考数学文科知识网络

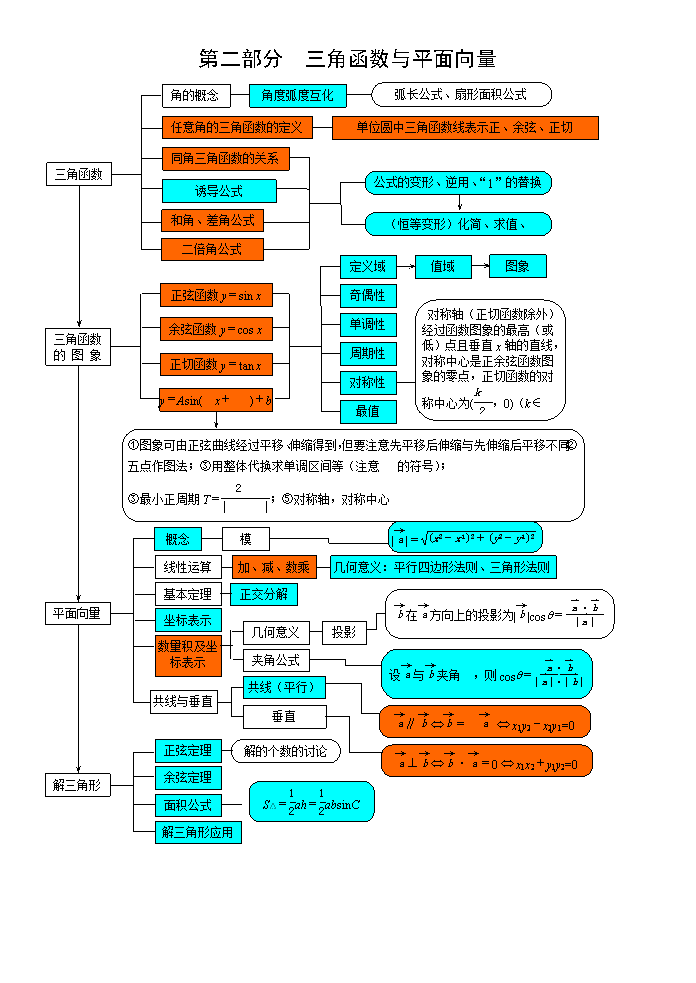
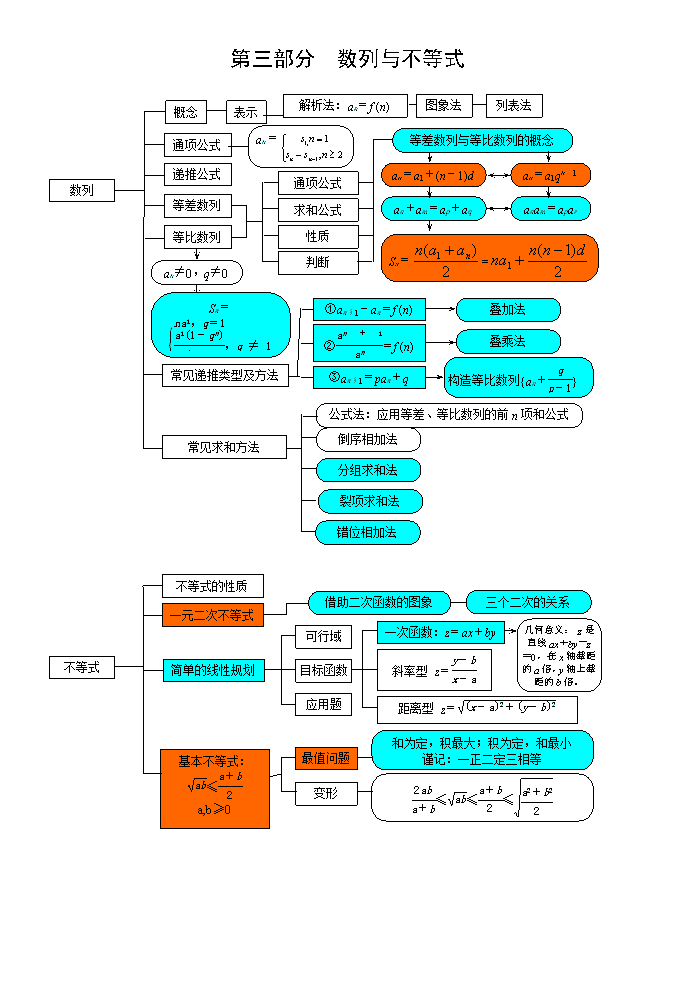
第一部分 集合、函数、导数 表示方法 元素、集合间的关系 概念 数轴、Venn图、函数图象、不等式解集 运算：交、并、补 集合 解析法 确定性、互异性、无序性 性质 列表法 分母、偶次方根、指、对数 表示 概念 映射 定义域 图象法 待定系数、换元法求解析式 对应关系 三要素 结合函数图像、单调性、导数求值域 值域 ‎1、函数在某个区间递增(或减)与单调区间是某个区间的含义不同；2、证明单调性：作差（商）、导数法 单调性 定义域关于原点对称，在x＝0处有定义的奇函数f (0)＝0‎ 奇偶性 周期为T的函数→f (x+T)＝f (x)‎ 周期性 性质 X、Y轴、原点、直线y=x 对称性 二次函数、基本不等式、双勾函数、‎ 三角函数有界性、数形结合、导数.‎ 函数 最值 平移变换 一次、二次函数、反比例函数 图象及其变换 对称变换 指数为1、2、3、-1、1/2幂函数 图像和性质 幂函数概念 伸缩变换 翻折变换 基本初等函数 概念、图象、‎ 性质和应用 幂运算、指数函数 对数概念、运算 对数函数 换底公式、反函数 求值、单调性、不等式、零点 分段函数 零点、二分法 函数与方程 建立函数模型 函数的应用 几何意义 导数的概念 三次函数的性质、图象与应用 基本初等函数的导数公式 导数的运算法则 导数 导数的正负与单调性的关系 单调性 导数的应用 极值 最值 生活中的优化问题 第二部分 三角函数与平面向量 角度弧度互化 弧长公式、扇形面积公式 角的概念 单位圆中三角函数线表示正、余弦、正切 任意角的三角函数的定义 同角三角函数的关系 同角三角函数的关系 诱导公式 公式的变形、逆用、“1”的替换 三角函数 ‎（恒等变形）化简、求值、‎ 和角、差角公式 二倍角公式 图象 值域 定义域 正弦函数y＝sin x ‎=‎ 奇偶性 余弦函数y＝cos x ‎ 对称轴（正切函数除外）经过函数图象的最高（或低）点且垂直x轴的直线，对称中心是正余弦函数图象的零点，正切函数的对称中心为(，0)（k∈Z）.‎ 单调性 周期性 三角函数 的 图 象 对称性 正切函数y＝tan x y＝Asin(wx＋j )＋b 最值 ‎①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；②五点作图法；③用整体代换求单调区间等（注意w 的符号）；‎ ‎③最小正周期T＝；⑤对称轴，对称中心 ‎||＝ 模 概念 几何意义：平行四边形法则、三角形法则 加、减、数乘 线性运算 正交分解 在方向上的投影为||cosq＝ 基本定理 坐标表示 平面向量 数量积及坐标表示 投影 几何意义 夹角公式 设与夹角q，则cosq＝ 共线（平行）‎ 共线与垂直 ∥Û＝l Û x1y2－x2y1=0‎ 垂直 解的个数的讨论 正弦定理 ⊥Û·＝0 Û x1x2＋y1y2=0‎ S△＝ah＝absinC 余弦定理 解三角形 面积公式 解三角形应用 第三部分 数列与不等式 列表法 解析法：an＝f (n)‎ 图象法 表示 概念 an＝‎ 等差数列与等比数列的概念 通项公式 an＝a1qn－1‎ an＝a1＋(n－1)d 通项公式 递推公式 数列 anam＝apar an＋am＝ap＋aq 求和公式 等差数列 Sn＝=‎ 等比数列 性质 an≠0，q≠0‎ 判断 Sn＝ ‎①an＋1－an＝f (n)‎ 叠加法 ‎②＝f (n)‎ 叠乘法 ‎③an＋1＝pan＋q 构造等比数列{an＋}‎ 常见递推类型及方法 公式法：应用等差、等比数列的前n项和公式 倒序相加法 常见求和方法 分组求和法 裂项求和法 错位相加法 三个二次的关系 借助二次函数的图象 不等式的性质 几何意义： z是直线ax＋by－z＝0，在x轴截距的a倍，y轴上截距的b倍。‎ 一元二次不等式 一次函数：z＝ax＋by 可行域 斜率型 z＝ 目标函数 简单的线性规划 不等式 应用题 距离型 z＝ 基本不等式：‎ ≤ a,b≥0‎ 和为定，积最大；积为定，和最小 谨记：一正二定三相等 最值问题 ≤≤≤ 变形 第四部分 解析几何 过两点的直线斜率公式 倾斜角和斜率 重合 x1y2－x2y1＝0‎ x1y2－x2y1≠0‎ 平行 位置关系 直线的方程 截距 x1x2＋y1y2＝0‎ 相交 垂直 注意：截距可正、可负，也可为0.‎ 点斜式：y－y0＝k(x－x0)‎ 注意各种形式的转化和运用范围.‎ 斜截式：y＝kx＋b 两点式：＝ 直线方程的形式 截距式：＋＝1‎ 两直线的交点 一般式：Ax＋By＋C＝0‎ 平行线间距离：‎ d＝ 点到线的距离：‎ d＝，‎ 距离 圆的标准方程 D＜0，或d＞r 相离 圆的一般方程 D＝0，或d＝r 相切 直线与圆的位置关系 圆的方程 D＞0，或d＜r 相交 两圆的位置关系 轨迹方程的求法：直接法、定义法、相关点法 曲线与方程 定义及标准方程 椭圆 圆锥曲线 范围、对称性、顶点、焦点、长轴（实轴）、短轴（虚轴）、渐近线（双曲线）、‎ 准线（只要求抛物线）、离心率 性质 双曲线 抛物线 弦长、弦的中点、韦达定理、判别式 求轨迹问题，定点问题、定值问题等 直线和圆锥曲线的位置关系 第五部分 立体几何 正棱柱、长方体、正方体 棱柱 柱体 长对正 高平齐 宽相等 三视图 圆柱 斜二侧法画直观图 棱台 台体 侧面积、表面积 圆台 空间几何体 三棱锥、四面体、正四面体 棱锥 锥体 体积 球 圆锥 点在直线上 点在直线外 点与线 点在面内 点在面外 点与面 只有一个公共点 相交 共面直线 没有公共点 平行 异面直线 线与线 没有公共点 平行 直线在平面外 有公共点 相交 线与面 空间点、‎ 线、面的 位置关系 直线在平面内 平行 面与面 相交 线线 平行 线面 平行 面面 平行 线线 垂直 线面 垂直 面面 垂直 平行关系的相互转化 垂直关系的相互转化 ‎ （定理熟悉了吗？）‎ 范围：(0°，90°]‎ 异面直线所成的角 范围：[0°，90°]‎ 直线与平面所成的角 空间的角 范围：[0°，180°]‎ 二面角 点到面的距离 空间的距离 相互之间的转化 直线与平面的距离 平行平面之间的距离 第六部分 统计与概率 共同特点：抽样过程中每个个体被抽到的可能性（概率）相等 简单随机抽样 抽签法 系统抽样 随机数表法 随机抽样 分层抽样 频率分布表和频率分布直方图、折线图 总体密度曲线 样本频率分布估计总体 茎叶图 用样本估计总体 统计 众数、中位数、平均数 样本数字特征估计总体 方差、标准差 回归直线 散点图 两个变量的线性相关 变量间的相关关系 列联表（2×2）独立性分析 互斥事件P(A+B)= P(A)+ P(B)‎ P(`A)＝1－P(A)‎ 对立事件 概率的基本性质 古典概型 概率 几何概型 用随机模拟法求概率 第七部分 其他部分内容 归纳 加、减、乘、除、乘方 运算 概念 复 数 辗转相除法、更相减损术、秦九韶算法、进位制 算法案例 基本算法语言 程序框图 算法的特征 算法语言 命题 循环结构 条件结构 顺序结构 简易逻辑 全称量词与存在量词 全真才真 有真就真 原命题：若p则q 逆命题：若q则p 否命题：若Øp则Øq 逆命题：若Øq则Øp 互逆 互逆 互否 互否 互为逆否 等价关系 猜想 非：Ø p 且：p Ù q 或：p Ú q 复合命题 条件 关系 充分非必要条件、必要非充分条件、充要条件 推理与证明 证明 推理 反证法 间接证明 由因导果 分析法 综合法 直接证明 大前提、小前提、结论 三段论 类比 演绎推理 合情推理 执果索因（要证。。。只需证。。。）‎ ‎ ‎ 复数代数表示法、加减法的几何意义 虚数、纯虚数、实部、虚部、实轴、虚轴、模、共轭复数、相等复数