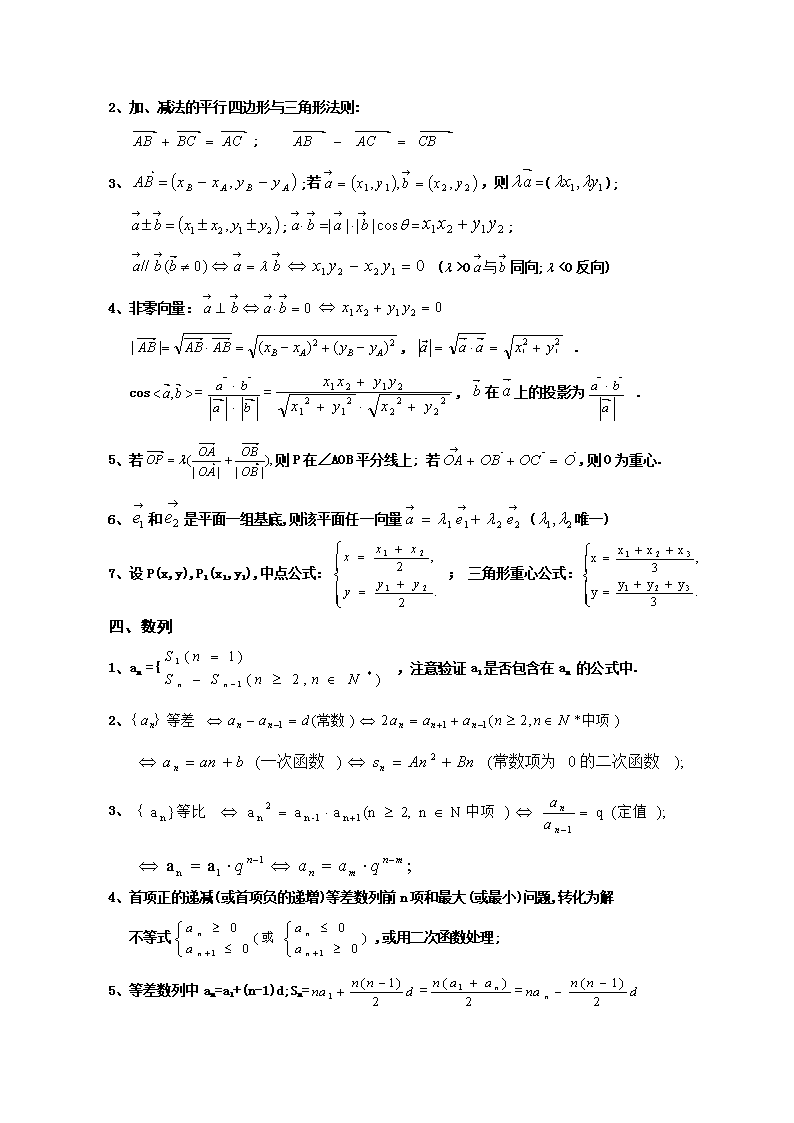高中高考文科数学知识点总结提纲
一、集合与逻辑1、区分集合中元素的形式.如:;;.2、条件为,在讨论的时候不要忘了的情况.3、;;CUA={x|x∈U但xA}.4、A∩B=AA∪B=BAB.5、含n个元素的集合的子集个数为2n,真子集(非空子集)个数为2n-1;6、逻辑联结词(“或”、“且”、“非”):复合命题的形式:p或q(同假为假,否则为真);p且q(同真为真,否则为假);非p(记”┑p”,与p真假相反).7、原命题:若p则q;逆命题:若q则p;否命题:若p则q;逆否命题:若q则p;互为逆否的两个命题是等价的.8、注意命题的否定与它的否命题的区别:命题的否定是;否命题是命题“p或q”的否定是“┐P且┐Q”,“p且q”的否定是“┐P或┐Q”.9、若则p是q的充分条件;若则p是q的必要条件;若则p是q的充要条件.二、不等式1、a>ba-b>0;a
b,c>da+c>b+d,a-d>b-c;3、a>b,c>0ac>bc,a>b,c<0acb>0,c>d>0ac>bd,;5、,,n∈N+6、重要不等式:①;②;③,则;ab.求最值:①一正二定三取等,若等号取不到则用单调性;②积定和最小,和定积最大.7、证法:①比较法(差法):作差--变形(分解或通分配方)---定号,常用来比较两式的大小。②综合法--由因导果;③分析法--执果索因;④反证法--正难则反。8、ax2+bx+c>0(a>0)若△>0,x1x2};若△<0,则解集为R;ax2+bx+c<0(a>0)若△>0,x10时,Ax+By+C>0表示直线的斜右侧区域;Ax+By+C<0表示直线的斜左侧区域;求最优解时注意:①目标函数值≠截距;②目标函数斜率与区域边界斜率的大小关系.三、平面向量1、向量定义、向量模、零向量、单位向量、相反向量、共线向量、相等向量
2、加、减法的平行四边形与三角形法则:;3、;若,则=();;=;(>0同向;<0反向)4、非零向量:,.cos==,在上的投影为.5、若则P在∠AOB平分线上;若,则O为重心.6、和是平面一组基底,则该平面任一向量(唯一)7、设P(x,y),P1(x1,y1),中点公式:;三角形重心公式:四、数列1、an={,注意验证a1是否包含在an的公式中.2、3、4、首项正的递减(或首项负的递增)等差数列前n项和最大(或最小)问题,转化为解不等式,或用二次函数处理;5、等差数列中an=a1+(n-1)d;Sn===
等比数列中an=a1qn-1;当q=1,Sn=na1;当q≠1,Sn==;6.等差数列中,an=am+(n-m)d,;当m+n=p+q,am+an=ap+aq;等比数列中,an=amqn-m;当m+n=p+q,aman=apaq;7.等差三数设为:a-d,a,a+d;等比三数可设为:a/q,a,aq;8.数列求和时关键要看通项的结构,常用方法:公式、分组、裂项相消、错位相减、倒序相加.求通项常用法:公式、迭加、迭乘、构造等比,如:an=kan-1+b(k≠0,k≠1).9.常用结论:1),2),3)4);5);五、概率与统计1、必然事件P(A)=1,不可能事件P(A)=0,随机事件的定义00则正相关,r<0则负相关.7、在频率分布直方图中:①小矩形的面积=组距=频率,所有小矩形面积的和=1;②众数是最高矩形的中点的横坐标;③中位数的左边与右边的直方图的面积相等,可以由此估计中位数的值;
六、三角函数1、终边相同(β=2kπ+α);终边落在坐标轴上的角(如α=);其中。α、关系(如:α终边在一、二象限,则终边在一或三象限).2、掌握正余弦、正切图象和性质:定义域、值域、周期、奇偶性、单调性、最值;3、函数=b()的图像掌握:①五点法作图;②周期T=;③当φ=kπ时,奇函数;当φ=kπ+时偶函数;④对称轴处取最值,中心处值为b,余弦正切可类比正弦;⑤变换:4、=;L弧长=R;S扇=LR=R2(其中角为弧度制);π=1800,1弧=57.305、同角基本关系:⑴商的关系:①②③==⑵平方关系:号规律:一全正,二正弦,三是切,四余弦;6、诱导公式简记:奇变偶不变,符号看象限.(注意:公式中始终视a为锐角)7、和差倍公式:,;,,降幂公式:;.辅助角公式:8、正弦定理:2R===;余弦定理:a=b+c-2bc,等;
面积公式:。七、函数与导数1、映射的概念(象唯一,原象未必有且也未必唯一),函数的概念(三要素).2、分数指数幂:;(,且),运算法则:as·at=as+t;(as)t=ast;(ab)s=asbs;(s,t∈Q,a>0)3、对数:logaN=bab=N(a>0,a≠1,N>0);=N;logaab=b;;运算法则:logaMn=nlogaM;logaMN=logaM+logaN;loga=logaM-logaN;换底公式:.推论:,4、指数函数y=ax与对数函数y=logax互为反函数(a>0,a≠1),它们的图象关于直线对称。名称图过定点定义域值域性质y=ax(0,1)RR+a>1增;00时增函数;a<0时减函数;b=0时奇函数;6、二次函数①三种形式:一般式:f(x)=ax2+bx+c(对称轴x=-b/2a,a≠0);顶点式:f(x)=a(x-h)2+k;零点式:f(x)=a(x-x1)(x-x2);②区间上的最值:讨论开口方向,对称轴与区间的相对位置关系;③实根分布:先画图再研究△>0、轴与区间关系、区间端点函数值符号。7、反比例函数:平移(中心为(b,a))8、函数是奇函数:;,9、单调性:①定义法:x1,x2∈=[a,b],则f(x)在[a,b]上递增(减)当时
;②导数法:函数y=f(x)在某区间内可导,若,则为增函数;若,则f(x)递减;③复合函数由同增异减判定,别忘记分析定义域.10、f(x)是偶函数f(-x)=f(x)=f(|x|);f(x)是奇函数f(-x)=-f(x);定义域中含零的奇函数过原点,(f(0)=0);判断奇偶性时要注意:①定义域关于原点对称否;②对于对数型函数用f(x)±f(-x)=0;奇函数在对称区间内单调性相同;偶函数在对称区间内单调性相反;奇函数的图像关于原点对称,偶函数的图像关于Y轴对称。函数关于轴的对称曲线方程为;函数关于轴的对称曲线方程为;函数关于原点的对称曲线方程为;11、若y=f(x)满足f(x+a)=f(a-x)(或f(x+2a)=f(-x)),则f(x)关于轴x=a对称;若y=f(x)满足f(x+a)=-f(a-x)(或f(x+2a)=-f(-x)),则f(x)关于点(a,0)对称。12、周期性:y=f(x)满足f(x+a)=f(x-a)或f(x±2a)=f(x)恒成立,则2a为周期;若y=f(x)满足f(x+a)=-f(x)(或f(x+a)=),则2a为f(x)的一个周期;若y=f(x)有两个对称中心,或有两条对称轴,或一个中心一条轴,则它有周期,可类比三角函数记忆。13、图形变换:y=f(x)→y=|f(x)|,把x轴上方的图象保留,x轴下方的图象关于x轴对称得到上方图象;y=f(x)→y=f(|x|),把y轴右边图象保留,并将y轴右边部分关于y轴对称得到左方图象.14、恒成立问题与存在问题常常转化为求函数的最值来解决,若能参变分离则分离。一般步骤:①分离参数;②求最值;a≥f(x)恒成立a≥[f(x)]max,;f(x)恒成立a≤[f(x)]min;存在使得[f(x)]max;存在使得[f(x)]min;15、y=f(x)在点x0处的导数几何意义:k=f/(x0)表示曲线y=f(x)在点P(x0,f(x0))处切线的斜率。导数瞬时变化率。V=s/(t)表示t时刻即时速度。16、基本公式:
法则:17、导数应用:⑴求切线斜率;⑵研究单调性步骤:分析y=f(x)定义域;求导数;解不等式f/(x)>0得增区间;解不等式f/(x)<0得减区间;⑶求极值、最值步骤:求导数;求的根;检验在根左右两侧符号:若左正右负,则f(x)在该根处取极大值;若左负右正,则f(x)在该根处取极小值;最后把极值与区间端点函数值比较,最大的为最大值,最小的是最小值.八、立体几何1、平面的基本性质:三个公理及推论;共点、共线、共面问题;2、斜二测作图法;几何体的三视图:理解三视图的投影规律“长对正,高平齐,宽相等”的含义.3、位置关系:①空间两直线:平行、相交、异面;②直线与平面:aα、aα(a∥α、a∩α=A);③平面与平面:α∥β、α∩β=a;4、求空间角与距离几何法步骤:一作、二证、三算.①异面直线所成角(00,900]:平移法求角,有中点多用中位线;②线面角[00,900]:作平面的垂线找射影;5、平面图形翻折(展开):注意翻折(展开)后在同一平面图形中角度、长度不变;6、长方体:对角线长;正方体和长方体外接球直径=体对角线的长;7、正方体、长方体、特殊椎体的外接球面积8、常用定理:①线面平行:;;;②线线平行:;;;;③面面平行:;;④线线垂直:;所成角为900;⑤线面垂直:;;;
⑥面面垂直:;⑤线线平行线面平行面面平行;⑥线线垂直线面垂直面面垂直。九、解析几何1、倾斜角α∈[0,π),α=900斜率不存在;斜率k=tanα=;理解倾斜角和斜率的关系。2、直线方程:点斜式:y-y1=k(x-x1);斜截式:y=kx+b;一般式:Ax+By+C=0;截距式:(a≠0;b≠0);注意:求直线方程时要防止由于零截距和无斜率造成丢解。3、两直线平行和垂直:①若l1:y=k1x+b1,l2:y=k2x+b2,则l1∥l2k1=k2,b1≠b2;l1⊥l2k1k2=-1;②若l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,且A1、A2、B1、B2都不为零,则l1⊥l2A1A2+B1B2=0;l1∥l2;(k不存在或A1、A2、B1、B2为0时需讨论)③l1∥l2,则化为同x、y系数后再求距离:d=4、点线距:d=;5、圆:标准方程:(x-a)2+(y-b)2=r2;一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0)6、直线与圆关系,常常化为弦心距与半径关系,如:用垂径定理,构造Rt△解决弦长问题;又:d>r相离;d=r相切;dr+R两圆相离;d=r+R两圆相外切;|R-r|b>0);②定义:|PF1|+|PF2|=2a>2c;③e=,a2=b2+c2;④椭圆上距焦点最近距离:a-c,最远距离:a+c;9、双曲线:①方程(a,b>0);②定义:||PF1|-|PF2||=2a<2c;③e=,c2=a2+b2;④渐近线:或;焦点到渐近线的距离为b;
10、抛物线:①方程y2=2px;②定义:|PF|=d准;③焦点F(,0),准线x=-;④焦点弦=x1+x2+p;y1y2=-p2,x1x2=其中A(x1,y1)、B(x2,y2);11、求动点的轨迹方程:①直接法:建系、设点、列式、化简、定范围;②定义法:说明动点P(x,y)满足已知曲线的定义,由定义直接写出方程;③相关点法:动点P(x,y)依赖于动点Q(x1,y1)而变化,Q(x1,y1)在已知曲线上,用x、y表示x1、y1,再将x1、y1代入已知曲线即得所求方程。