中考数学与圆有关的压轴题

中考数学与圆有关的压轴题

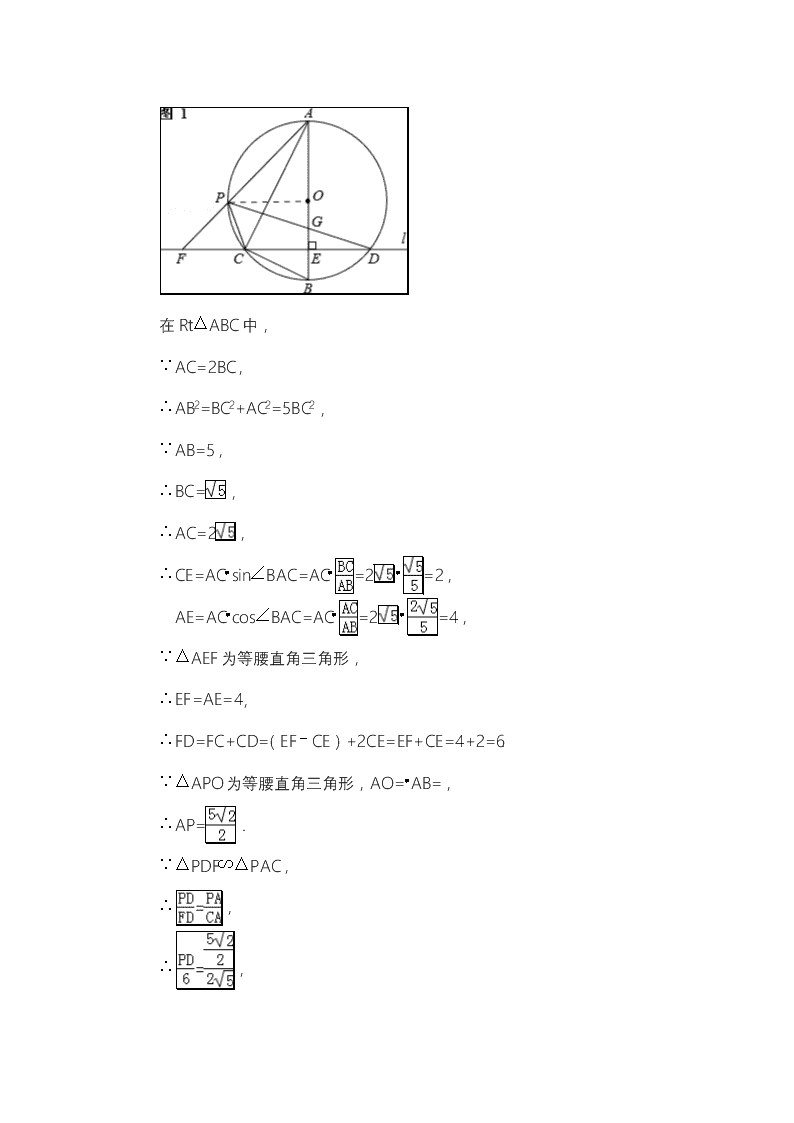
中考数学与圆有关的压轴题（解答题部分3）‎ ‎11．（2014•四川成都,第27题10分）如图，在⊙O的内接△ABC中，∠ACB=90°，AC=2BC，过C作AB的垂线l交⊙O于另一点D，垂足为E．设P是上异于A，C的一个动点，射线AP交l于点F，连接PC与PD，PD交AB于点G．‎ ‎（1）求证：△PAC∽△PDF；‎ ‎（2）若AB=5，=，求PD的长；‎ ‎（3）在点P运动过程中，设=x，tan∠AFD=y，求y与x之间的函数关系式．（不要求写出x的取值范围）‎ 考点：‎ 圆的综合题 分析：‎ ‎（1）证明相似，思路很常规，就是两个角相等或边长成比例．因为题中因圆周角易知一对相等的角，那么另一对角相等就是我们需要努力的方向，因为涉及圆，倾向于找接近圆的角∠DPF，利用补角在圆内作等量代换，等弧对等角等知识易得∠DPF=∠APC，则结论易证．‎ ‎（2）求PD的长，且此线段在上问已证相似的△PDF中，很明显用相似得成比例，再将其他边代入是应有的思路．利用已知条件易得其他边长，则PD可求．‎ ‎（3）因为题目涉及∠AFD与也在第一问所得相似的△PDF中，进而考虑转化，∠AFD=∠PCA，连接PB得∠AFD=∠PCA=∠PBG，过G点作AB的垂线，若此线过PB与AC的交点那么结论易求，因为根据三角函数或三角形与三角形ABC相似可用AG表示∠PBG所对的这条高线．但是“此线是否过PB与AC的交点”？此时首先需要做的是多画几个动点P，观察我们的猜想．验证得我们的猜想应是正确的，可是证明不能靠画图，如何求证此线过PB与AC的交点是我们解题的关键．常规作法不易得此结论，我们可以换另外的辅助线作法，先做垂线，得交点H，然后连接交点与B，再证明∠HBG=∠PCA=∠AFD．因为C、D关于AB对称，可以延长CG考虑P点的对称点．根据等弧对等角，可得∠HBG=∠PCA，进而得解题思路．‎ 解答：‎ ‎（1）证明：∵，‎ ‎∴∠DPF=180°﹣∠APD=180°﹣所对的圆周角=180°﹣所对的圆周角=所对的圆周角=∠APC．‎ 在△PAC和△PDF中，‎ ‎，‎ ‎∴△PAC∽△PDF．‎ ‎（2）解：如图1，连接PO，则由，有PO⊥AB，且∠PAB=45°，△APO、△AEF都为等腰直角三角形．‎ 在Rt△ABC中，‎ ‎∵AC=2BC，‎ ‎∴AB2=BC2+AC2=5BC2，‎ ‎∵AB=5，‎ ‎∴BC=，‎ ‎∴AC=2，‎ ‎∴CE=AC•sin∠BAC=AC•=2•=2，‎ ‎ AE=AC•cos∠BAC=AC•=2•=4，‎ ‎∵△AEF为等腰直角三角形，‎ ‎∴EF=AE=4，‎ ‎∴FD=FC+CD=（EF﹣CE）+2CE=EF+CE=4+2=6．‎ ‎∵△APO为等腰直角三角形，AO=•AB=，‎ ‎∴AP=．‎ ‎∵△PDF∽△PAC，‎ ‎∴，‎ ‎∴，‎ ‎∴PD=．‎ ‎（3）解：如图2，过点G作GH⊥AB，交AC于H，连接HB，以HB为直径作圆，连接CG并延长交⊙O于Q，‎ ‎∵HC⊥CB，GH⊥GB，‎ ‎∴C、G都在以HB为直径的圆上，‎ ‎∴∠HBG=∠ACQ，‎ ‎∵C、D关于AB对称，G在AB上，‎ ‎∴Q、P关于AB对称，‎ ‎∴，‎ ‎∴∠PCA=∠ACQ，‎ ‎∴∠HBG=∠PCA．‎ ‎∵△PAC∽△PDF，‎ ‎∴∠PCA=∠PFD=∠AFD，‎ ‎∴y=tan∠AFD=tan∠PCA=tan∠HBG=．‎ ‎∵HG=tan∠HAG•AG=tan∠BAC•AG==，‎ ‎∴y==x．‎ 点评：‎ 本题考查了圆周角、相似三角形、三角函数等性质，前两问思路还算简单，但最后一问需要熟练的解题技巧需要长久的磨练总结．总体来讲本题偏难，学生练习时加强理解，重点理解分析过程，自己如何找到思路．‎ ‎　‎ ‎12. （2014•湖北荆门,第24题12分）如图①，已知：在矩形ABCD的边AD上有一点O，OA=，以O为圆心，OA长为半径作圆，交AD于M，恰好与BD相切于H，过H作弦HP∥AB，弦HP=3．若点E是CD边上一动点（点E与C，D不重合），过E作直线EF∥BD交BC于F，再把△CEF沿着动直线EF对折，点C的对应点为G．设CE=x，△EFG与矩形ABCD重叠部分的面积为S．‎ ‎（1）求证：四边形ABHP是菱形；‎ ‎（2）问△EFG的直角顶点G能落在⊙O上吗？若能，求出此时x的值；若不能，请说明理由；‎ ‎（3）求S与x之间的函数关系式，并直接写出FG与⊙O相切时，S的值．‎ 第3题图 考点： 圆的综合题；含30度角的直角三角形；菱形的判定；矩形的性质；垂径定理；切线的性质；切线长定理；轴对称的性质；特殊角的三角函数值所有 专题： 压轴题．‎ 分析： （1）连接OH，可以求出∠HOD=60°，∠HDO=30°，从而可以求出AB=3，由HP∥AB，HP=3可证到四边形ABHP是平行四边形，再根据切线长定理可得BA=BH，即可证到四边形ABHP是菱形．‎ ‎（2）当点G落到AD上时，可以证到点G与点M重合，可求出x=2．‎ ‎（3）当0≤x≤2时，如图①，S=S△EGF，只需求出FG，就可得到S与x之间的函数关系式；当2＜x≤3时，如图④，S=S△GEF﹣S△SGR，只需求出SG、RG，就可得到S与x之间的函数关系式．当FG与⊙O相切时，如图⑤，易得FK=AB=3，KQ=AQ﹣AK=2﹣2+x．再由FK=KQ即可求出x，从而求出S．‎ 解答： 解：（1）证明：连接OH，如图①所示．‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠ADC=∠BAD=90°，BC=AD，AB=CD．‎ ‎∵HP∥AB，‎ ‎∴∠ANH+∠BAD=180°．‎ ‎∴∠ANH=90°．‎ ‎∴HN=PN=HP=．‎ ‎∵OH=OA=，‎ ‎∴sin∠HON==．‎ ‎∴∠HON=60°‎ ‎∵BD与⊙O相切于点H，‎ ‎∴OH⊥BD．‎ ‎∴∠HDO=30°．‎ ‎∴OD=2．‎ ‎∴AD=3．‎ ‎∴BC=3．‎ ‎∵∠BAD=90°，∠BDA=30°．‎ ‎∴tan∠BDA===．‎ ‎∴AB=3．‎ ‎∵HP=3，‎ ‎∴AB=HP．‎ ‎∵AB∥HP，‎ ‎∴四边形ABHP是平行四边形．‎ ‎∵∠BAD=90°，AM是⊙O的直径，‎ ‎∴BA与⊙O相切于点A．‎ ‎∵BD与⊙O相切于点H，‎ ‎∴BA=BH．‎ ‎∴平行四边形ABHP是菱形．‎ ‎（2）△EFG的直角顶点G能落在⊙O上．‎ 如图②所示，点G落到AD上．‎ ‎∵EF∥BD，‎ ‎∴∠FEC=∠CDB．‎ ‎∵∠CDB=90°﹣30°=60°，‎ ‎∴∠CEF=60°．‎ 由折叠可得：∠GEF=∠CEF=60°．‎ ‎∴∠GED=60°．‎ ‎∵CE=x，‎ ‎∴GE=CE=x．ED=DC﹣CE=3﹣x．‎ ‎∴cos∠GED===．‎ ‎∴x=2．‎ ‎∴GE=2，ED=1．‎ ‎∴GD=．‎ ‎∴OG=AD﹣AO﹣GD=3﹣﹣=．‎ ‎∴OG=OM．‎ ‎∴点G与点M重合．‎ 此时△EFG的直角顶点G落在⊙O上，对应的x的值为2．‎ ‎∴当△EFG的直角顶点G落在⊙O上时，对应的x的值为2．‎ ‎（3）①如图①，‎ 在Rt△EGF中，‎ tan∠FEG===．‎ ‎∴FG=x．‎ ‎∴S=GE•FG=x•x=x2．‎ ‎②如图③，‎ ED=3﹣x，RE=2ED=6﹣2x，‎ GR=GE﹣ER=x﹣（6﹣2x）=3x﹣6．‎ ‎∵tan∠SRG===，‎ ‎∴SG=（x﹣2）．‎ ‎∴S△SGR=SG•RG=•（x﹣2）•（3x﹣6）．‎ ‎=（x﹣2）2．‎ ‎∵S△GEF=x2，‎ ‎∴S=S△GEF﹣S△SGR ‎=x2﹣（x﹣2）2．‎ ‎=﹣x2+6x﹣6．‎ 综上所述：当0≤x≤2时，S=x2；当2＜x≤3时，S=﹣x2+6x﹣6．‎ 当FG与⊙O相切于点T时，延长FG交AD于点Q，过点F作FK⊥AD，垂足为K，如图④所示．‎ ‎∵四边形ABCD是矩形，‎ ‎∴BC∥AD，∠ABC=∠BAD=90°‎ ‎∴∠AQF=∠CFG=60°．‎ ‎∵OT=，‎ ‎∴OQ=2．‎ ‎∴AQ=+2．‎ ‎∵∠FKA=∠ABC=∠BAD=90°，‎ ‎∴四边形ABFK是矩形．‎ ‎∴FK=AB=3，AK=BF=3﹣x．‎ ‎∴KQ=AQ﹣AK=（+2）﹣（3﹣x）=2﹣2+x．‎ 在Rt△FKQ中，tan∠FQK==．‎ ‎∴FK=QK．‎ ‎∴3=（2﹣2+x）．‎ 解得：x=3﹣．‎ ‎∵0≤3﹣≤2，‎ ‎∴S=x2=×（3﹣）2‎ ‎=﹣6．‎ ‎∴FG与⊙O相切时，S的值为﹣6．‎ 点评： 本题考查了矩形的性质、菱形的性质、切线的性质、切线长定理、垂径定理、轴对称性质、特殊角的三角函数值、30°角所对的直角边等于斜边的一半、等腰三角形的性质等知识，综合性非常强．‎ ‎　‎ ‎13．（2014•莱芜，第23题10分）如图1，在⊙O中，E是弧AB的中点，C为⊙O上的一动点（C与E在AB异侧），连接EC交AB于点F，EB=（r是⊙O的半径）．‎ ‎（1）D为AB延长线上一点，若DC=DF，证明：直线DC与⊙O相切；‎ ‎（2）求EF•EC的值；‎ ‎（3）如图2，当F是AB的四等分点时，求EC的值．‎ 考点：‎ 圆的综合题．.‎ 专题：‎ 综合题．‎ 分析：‎ ‎（1）连结OC、OE，OE交AB于H，如图1，由E是弧AB的中点，根据垂径定理的推论得到OE⊥AB，则∠HEF+∠HFE=90°，由对顶相等得∠HFE=∠CFD，则∠HEF+∠CFD=90°，再由DC=DF得∠CFD=∠DCF，加上∠OCE=∠OEC，所以∠OCE+∠DCE=∠HEF+∠CFD=90°，于是根据切线的判定定理得直线DC与⊙O相切；‎ ‎（2）由弧AE=弧BE，根据圆周角定理得到∠ABE=∠BCE，加上∠FEB=∠BEC，于是可判断△EBF∽△ECB，利用相似比得到EF•EC=BE2=（r）2=r2；‎ ‎（3）如图2，连结OA，由弧AE=弧BE得AE=BE=r，设OH=x，则HE=r﹣x，根据勾股定理，在Rt△OAH中有AH2+x2=r2；在Rt△EAH中由AH2+（r﹣x）2=（r）2，利用等式的性质得x2﹣（r﹣x）2=r2﹣（r）2，即得x=r，则HE=r﹣r=r，在Rt△OAH中，根据勾股定理计算出AH=，由OE⊥AB得AH=BH，而F是AB的四等分点，所以HF=AH=，于是在Rt△EFH中可计算出EF=r，然后利用（2）中的结论可计算出EC．‎ 解答：‎ ‎（1）证明：连结OC、OE，OE交AB于H，如图1，‎ ‎∵E是弧AB的中点，‎ ‎∴OE⊥AB，‎ ‎∴∠EHF=90°，‎ ‎∴∠HEF+∠HFE=90°，‎ 而∠HFE=∠CFD，‎ ‎∴∠HEF+∠CFD=90°，‎ ‎∵DC=DF，‎ ‎∴∠CFD=∠DCF，‎ 而OC=OE，‎ ‎∴∠OCE=∠OEC，‎ ‎∴∠OCE+∠DCE=∠HEF+∠CFD=90°，‎ ‎∴OC⊥CD，‎ ‎∴直线DC与⊙O相切；‎ ‎（2）解：连结BC，‎ ‎∵E是弧AB的中点，‎ ‎∴弧AE=弧BE，‎ ‎∴∠ABE=∠BCE，‎ 而∠FEB=∠BEC，‎ ‎∴△EBF∽△ECB，‎ ‎∴EF：BE=BE：EC，‎ ‎∴EF•EC=BE2=（r）2=r2；‎ ‎（3）解：如图2，连结OA，‎ ‎∵弧AE=弧BE，‎ ‎∴AE=BE=r，‎ 设OH=x，则HE=r﹣x，‎ 在Rt△OAH中，AH2+OH2=OA2，即AH2+x2=r2，‎ 在Rt△EAH中，AH2+EH2=EA2，即AH2+（r﹣x）2=（r）2，‎ ‎∴x2﹣（r﹣x）2=r2﹣（r）2，即得x=r，‎ ‎∴HE=r﹣r=r，‎ 在Rt△OAH中，AH===，‎ ‎∵OE⊥AB，‎ ‎∴AH=BH，‎ 而F是AB的四等分点，‎ ‎∴HF=AH=，‎ 在Rt△EFH中，EF===r，‎ ‎∵EF•EC=r2，‎ ‎∴r•EC=r2，‎ ‎∴EC=r．‎ 点评：‎ 本题考查了圆的综合题：熟练掌握垂径定理及其推论、切线的判定定理和圆周角定理；会利用勾股定理进行几何计算，利用相似三角形的知识解决有关线段等积的问题．‎ ‎14. （2014•乐山，第26题12分）如图，⊙O1与⊙O ‎2外切与点D，直线l与两圆分别相切于点A、B，与直线 O1、O2相交于点M，且tan∠AM01=，MD=4．‎ ‎（1）求⊙O2的半径；‎ ‎（2）求△ADB内切圆的面积；‎ ‎（3）在直线l上是否存在点P，使△MO2P相似于△MDB？若存在，求出PO2的长；若不存在，请说明理由．‎ 考点：‎ 圆的综合题．.‎ 专题：‎ 综合题．‎ 分析：‎ ‎（1）连结O1A、O2B，设⊙O1的半径为r，⊙O2的半径为R，根据两圆相切的性质得到直线O1O2过点D，则MO2=MD+O2D=4+R，再根据切线的性质由直线l与两圆分别相切于点A、B得到O1A⊥AB，O2B⊥AB，然后根据特殊角的三角函数值得到∠AM01=30°，在Rt△MBO2中，根据含30度的直角三角形三边的关系得MO2=O2B=2R，于是有4+R=2R，解得R=4；‎ ‎（2）利用互余由∠AM02=30°得到∠MO2B=60°，则可判断△O2BD为等边三角形，所以BD=O2B=4，∠DBO2=60°，于是可计算出∠‎ ABD=30°，同样可得 ‎∠MO1A=60°，利用三角形外角性质可计算得∠O1AD=∠MO1A=30°，则∠DAB=60°，所以∠ADB=90°，在Rt△ABD中，根据含30度的直角三角形三边的关系得AD=BD=4，AB=2AD=8，利用直角三角形内切圆的半径公式得到△ADB内切圆的半径==2﹣2，然后根据圆的面积公式求解；‎ ‎（3）先在Rt△MBO2中，根据含30度的直角三角形三边的关系得MB=O2B=12，然后分类讨论：△MO2P与△MDB有一个公共角，当△MO2P∽△MDB时，利用相似比可计算出O2P=8；当△MO2P∽△MBD时，利用相似比可计算出O2P=8．‎ 解答：‎ 解：（1）连结O1A、O2B，如图，设⊙O1的半径为r，⊙O2的半径为R，‎ ‎∵⊙O1与⊙O2外切与点D，‎ ‎∴直线O1O2过点D，‎ ‎∴MO2=MD+O2D=4+R，‎ ‎∵直线l与两圆分别相切于点A、B，‎ ‎∴O1A⊥AB，O2B⊥AB，‎ ‎∵tan∠AM01=，‎ ‎∴∠AM01=30°，‎ 在Rt△MBO2中，MO2=O2B=2R，‎ ‎∴4+R=2R，解得R=4，‎ 即⊙O2的半径为4；‎ ‎（2）∵∠AM02=30°，‎ ‎∴∠MO2B=60°，‎ 而O2B=O2D，‎ ‎∴△O2BD为等边三角形，‎ ‎∴BD=O2B=4，∠DBO2=60°，‎ ‎∴∠ABD=30°，‎ ‎∵∠AM01=30°，‎ ‎∴∠MO1A=60°，‎ 而O1A=O1D，‎ ‎∴∠O1AD=∠O1DA，‎ ‎∴∠O1AD=∠MO1A=30°，‎ ‎∴∠DAB=60°，‎ ‎∴∠ADB=180°﹣30°﹣60°=90°，‎ 在Rt△ABD中，AD=BD=4，AB=2AD=8，‎ ‎∴△ADB内切圆的半径===2﹣2，‎ ‎∴△ADB内切圆的面积=π•（2﹣2）2=（16﹣8）π；‎ ‎（3）存在．‎ 在Rt△MBO2中，MB=O2B=×4=12，‎ 当△MO2P∽△MDB时，=，即=，解得O2P=8；‎ 当△MO2P∽△MBD时，=，即=，解得O2P=8，‎ 综上所述，满足条件的O2P的长为8或8．‎ 点评：‎ 本题考查了圆的综合题：熟练掌握切线的性质、两圆相切的性质和直角三角形内切圆的半径；会利用含30度的直角三角形三边的关系和三角形相似比进行几何计算；会运用分类讨论的思想解决数学问题．‎ 单纯的课本内容，并不能满足学生的需要，通过补充，达到内容的完善 ‎ 教育之通病是教用脑的人不用手，不教用手的人用脑，所以一无所能。教育革命的对策是手脑联盟，结果是手与脑的力量都可以大到不可思议。‎