2020年中考数学压轴题:创新型与新定义综合问题考点专练
2020 年中考数学压轴题:创新型与新定义综合问题考点专练
【考点 1】几何综合探究类阅读理解问题
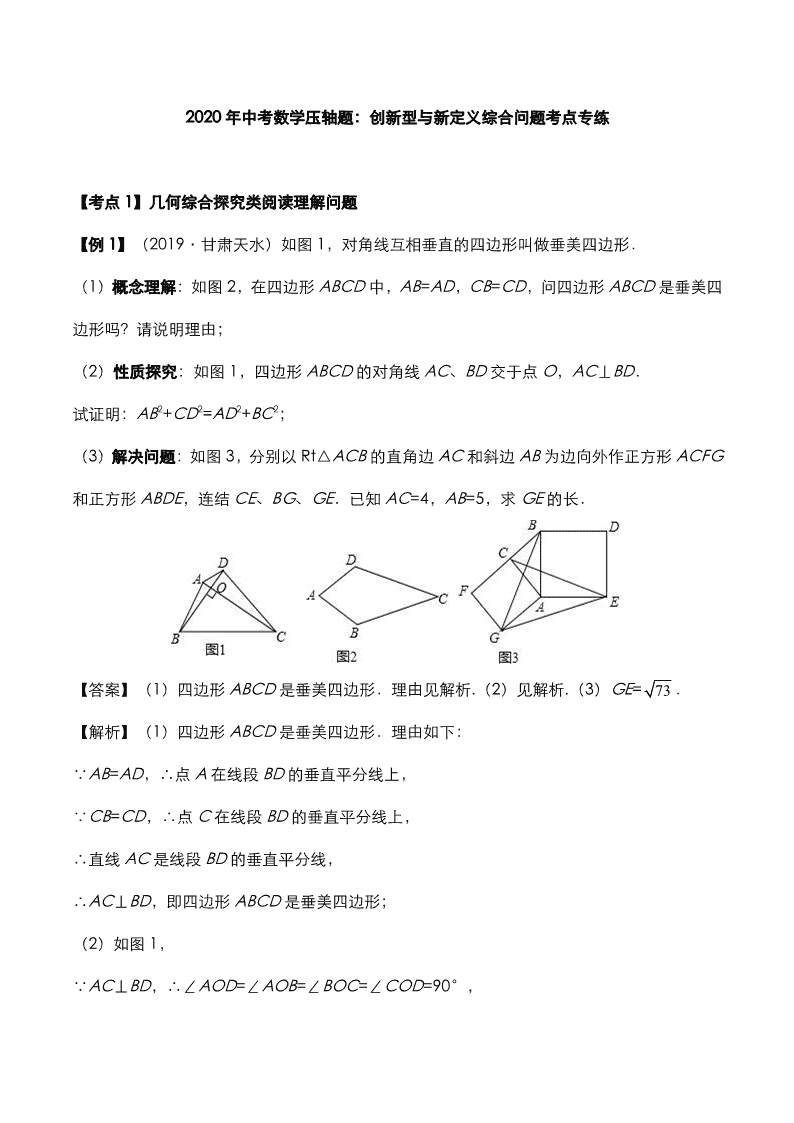
【例 1】(2019·甘肃天水)如图 1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图 2,在四边形 ABCD 中,AB=AD,CB=CD,问四边形 ABCD 是垂美四
边形吗?请说明理由;
(2)性质探究:如图 1,四边形 ABCD 的对角线 AC、BD 交于点 O,AC⊥BD.
试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图 3,分别以 Rt△ACB 的直角边 AC 和斜边 AB 为边向外作正方形 ACFG
和正方形 ABDE,连结 CE、BG、GE.已知 AC=4,AB=5,求 GE 的长.
【答案】(1)四边形 ABCD 是垂美四边形.理由见解析.(2)见解析.(3)GE= 73 .
【解析】(1)四边形 ABCD 是垂美四边形.理由如下:
∵AB=AD,∴点 A 在线段 BD 的垂直平分线上,
∵CB=CD,∴点 C 在线段 BD 的垂直平分线上,
∴直线 AC 是线段 BD 的垂直平分线,
∴AC⊥BD,即四边形 ABCD 是垂美四边形;
(2)如图 1,
∵AC⊥BD,∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AB2+CD2=AO2+BO2+DO2+CO2=AD2+BC2,
∴AD2+BC2=AB2+CD2;
(3)连接 CG、BE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△GAB 和△CAE 中,
AG AC
GAB CAE
AB AE
,
∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,
∴∠ABG+∠AME=90°,即 CE⊥BG,
∴四边形 CGEB 是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,
∵AC=4,AB=5,∴BC=3,CG=4 2 ,BE=5 2 ,
∴GE2=CG2+BE2-CB2=73,∴GE= 73 .
【名师点睛】(1)根据垂直平分线的判定定理证明即可;(2)根据垂直的定义和勾股定理解
答即可;
(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.本题考查的是正方形的性质、
全等三角形的判定和性质、垂直的定义、勾股定理的应用,正确理解垂美四边形的定义、灵活
运用勾股定理是解题的关键.
【变式 1-1】(2019·甘肃白银)阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边△ABC 中,M 是 BC 边上一点(不含端点 B,C),N 是△ABC 的外
角∠ACH 的平分线上一点,且 AM=MN.求证:∠AMN=60°.
点拨:如图②,作∠CBE=60°,BE 与 NC 的延长线相交于点 E,得等边△BEC,连接 EM.易
证:△ABM≌△EBM(SAS),可得 AM=EM,∠1=∠2;又 AM=MN,则 EM=MN,可得∠
3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所
以∠5+∠6=120°,即:∠AMN=60°.
问题:如图③,在正方形 A1B1C1D1 中,M1 是 B1C1 边上一点(不含端点 B1,C1),N1 是正方
形 A1B1C1D1 的外角∠D1C1H1 的平分线上一点,且 A1M1=M1N1.求证:∠A1M1N1=90°.
【答案】见解析.
【解析】延长 A1B1 至 E,使 EB1=A1B1,连接 EM1、EC1,
如图所示:
则 EB1=B1C1,∠EB1M1=90°=∠A1B1M1,
∴△EB1C1 是等腰直角三角形,
∴∠B1EC1=∠B1C1E=45°,
∵N1 是正方形 A1B1C1D1 的外角∠D1C1H1 的平分线上一点,
∴∠M1C1N1=90°+45°=135°,
∴∠B1C1E+∠M1C1N1=180°,
∴E、C1、N1 三点共线,
在△A1B1M1 和△EB1M1 中,
1 1 1
1 1 1 1 1
1 1 1 1
A B EB
A B M EB
M
M
B M B
,
∴△A1B1M1≌△EB1M1(SAS),
∴A1M1=EM1,∠1=∠2,
∵A1M1=M1N1,∴EM1=M1N1,∴∠3=∠4,
∵∠2+∠3=45°,∠4+∠5=45°,∴∠1=∠2=∠5,
∵∠1+∠6=90°,∴∠5+∠6=90°,
∴∠A1M1N1=180°﹣90°=90°.
【名师点睛】此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰
直角三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质等知识;本题综合性
强,熟练掌握正方形的性质,通过作辅助线构造三角形全等是解本题的关键.
【变式 1-2】(2019·湖北咸宁)定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
(1)如图 1,点 A,B,C 在⊙O 上,∠ABC 的平分线交⊙O 于点 D,连接 AD,CD.
求证:四边形 ABCD 是等补四边形;
探究:
(2)如图 2,在等补四边形 ABCD 中,AB=AD,连接 AC,AC 是否平分∠BCD?请说明理
由.
运用:
(3)如图 3,在等补四边形 ABCD 中,AB=AD,其外角∠EAD 的平分线交 CD 的延长线于
点 F,CD=10,AF=5,求 DF 的长.
【解析】(1)如图 1,∵四边形 ABCD 为圆内接四边形,
∴∠A+∠C=180°,∠ABC+∠ADC=180°,
∵BD 平分∠ABC,∴∠ABD=∠CBD,∴ AD CD ,∴AD=CD,
∴四边形 ABCD 是等补四边形;
(2)AD 平分∠BCD,理由如下:
如图 2,过点 A 分别作 AE⊥BC 于点 E,AF 垂直 CD 的延长线于点 F,
则∠AEB=∠AFD=90°,
∵四边形 ABCD 是等补四边形,∴∠B+∠ADC=180°,
又∠ADC+∠ADF=180°,∴∠B=∠ADF,
∵AB=AD,∴△ABE≌△ADF(AAS),∴AE=AF,
∴AC 是∠BCF 的平分线,即 AC 平分∠BCD;
(3)如图 3,连接 AC,
∵四边形 ABCD 是等补四边形,∴∠BAD+∠BCD=180°,
又∠BAD+∠EAD=180°,∴∠EAD=∠BCD,
∵AF 平分∠EAD,∴∠FAD= 1
2 ∠EAD,
由(2)知,AC 平分∠BCD,
∴∠FCA= 1
2 ∠BCD,∴∠FCA=∠FAD,
又∠AFC=∠DFA,∴△ACF∽△DAF,
∴ AF CF
DF AF
,即 5 10
5
DF
DF
,∴DF=5 2 ﹣5.
【名师点睛】本题考查了新定义等补四边形,圆的有关性质,全等三角形的判定与性质,角平
分线的判定,相似三角形的判定与性质等,解题关键是要能够通过自主学习来进行探究,运用
等.
【考点 2】代数类新定义及阅读理解型问题
【例 2】(2019•自贡)阅读下列材料:小明为了计算 1+2+22+…+22017+22018 的值,采用以下
方法:
设 S=1+2+22+…+22017+22018①,
则 2S=2+22+…+22018+22019②,
②–①得 2S–S=S=22019–1,
∴S=1+2+22+…+22017+22018=22019–1.
请仿照小明的方法解决以下问题:
(1)1+2+22+…+29=__________;
(2)3+32+…+310=__________;
(3)求 1+a+a2+…+an 的和(a>0,n 是正整数),请写出计算过程.
【答案】(1)210–1;(2)
113 1
2
;(3)a=1 时,S=n+1;a≠1 时,S=
1 1
1
na
a
.
【解析】(1)设 S=1+2+22+…+29①,
则 2S=2+22+…+210②,
②–①得 2S–S=S=210–1,
∴S=1+2+22+…+29=210–1;
故答案为:210–1;
(2)设 S=3+3+32+33+34+…+310①,
则 3S=32+33+34+35+…+311②,
②–①得 2S=311–1,
所以 S=
113 1
2
,
即 3+32+33+34+…+310=
113 1
2
;
故答案为:
113 1
2
;
(3)设 S=1+a+a2+a3+a4+…+an①,
则 aS=a+a2+a3+a4+…+an+an+1②,
②–①得:(a–1)S=an+1–1,
a=1 时,不能直接除以 a–1,此时原式等于 n+1;
a≠1 时,a–1 才能做分母,所以 S=
1 1
1
na
a
,
即 1+a+a2+a3+a4+…+an=
1 1
1
na
a
.
【名师点睛】根据题目给出的信息,提炼解题方法.认真观察、仔细思考,善用联想,利用类
比的方法是解决这类问题的方法.
【变式 2-1】(2019•随州)若一个两位数十位、个位上的数字分别为 m,n,我们可将这个
两位数记为 mn ,易知 mn =10m+n;同理,一个三位数、四位数等均可以用此记法,如
abc=100a+10b+c.
【基础训练】
(1)解方程填空:
①若 2x + 3x =45,则 x=__________;
②若7y – 8y =26,则 y=__________;
③若 93t +5 8t =13 1t ,则 t=__________;
【能力提升】
(2)交换任意一个两位数 mn 的个位数字与十位数字,可得到一个新数 nm ,则 mn + nm 一定
能被__________整除, mn – nm 一定能被__________整除, mn •nm –mn 一定能被
__________整除;(请从大于 5 的整数中选择合适的数填空)
【探索发现】
(3)北京时间 2019 年 4 月 10 日 21 时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极
大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求
个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数
和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为 325,则用
532–235=297),再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会
得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.
①该“卡普雷卡尔黑洞数”为__________;
②设任选的三位数为 abc(不妨设 a>b>c),试说明其均可产生该黑洞数.
【答案】(1)①2.②4.③7.(2)11;9;10.
【解析】(1)①∵ mn =10m+n,
∴若 2x + 3x =45,则 10×2+x+10x+3=45,
∴x=2,
故答案为:2.
②若7y – 8y =26,则 10×7+y–(10y+8)=26,
解得 y=4,
故答案为:4.
③由 abc=100a+10b+c,及四位数的类似公式得
若 93t +5 8t =13 1t ,则 100t+10×9+3+100×5+10t+8=1000×1+100×3+10t+1,
∴100t=700,
∴t=7,
故答案为:7.
(2)∵ mn + nm =10m+n+10n+m=11m+11n=11(m+n),
∴则 mn + nm 一定能被 11 整除,
∵ mn – nm =10m+n–(10n+m)=9m–9n=9(m–n),
∴ mn – nm 一定能被 9 整除.
∵ mn • nm –mn=(10m+n)(10n+m)–mn=100mn+10m2+10n2+mn–mn=10
(10mn+m2+n2)
∴ mn • nm –mn 一定能被 10 整除.
故答案为:11;9;10.
(3)①若选的数为 325,则用 532–235=297,以下按照上述规则继续计算,
972–279=693,
963–369=594,
954–459=495,
954–459=495,…
故答案为:495.
②当任选的三位数为 abc时,第一次运算后得:100a+10b+c–(100c+10b+a)=99(a–c),
结果为 99 的倍数,由于 a>b>c,故 a≥b+1≥c+2,
∴a–c≥2,又 9≥a>c≥0,
∴a–c≤9,
∴a–c=2,3,4,5,6,7,8,9,
∴第一次运算后可能得到:198,297,396,495,594,693,792,891,
再让这些数字经过运算,分别可以得到:
981–189=792,972–279=693,963–369=594,954–459–495,954–459=495…,
故都可以得到该黑洞数 495.
【名师点睛】本题是较为复杂的新定义试题,题目设置的问题较多,但解答方法大同小异,总
体中等难度略大.
【变式 2-2】(2019•济宁)阅读下面的材料:
如果函数 y=f(x)满足:对于自变量 x 的取值范围内的任意 x1,x2,
(1)若 x1
1).
小红通过观察反比例函数 y= 1
x 的图象,并运用几何知识得出结论:
AE+BG=2CF,CF>DF,
由此得出一个关于 1
1n , 1
1n , 2
n ,之间数量关系的命题:
若 n>1,则__________.
(2)证明命题
小东认为:可以通过“若 a﹣b≥0,则 a≥b”的思路证明上述命题.
小晴认为:可以通过“若 a>0,b>0,且 a÷b≥1,则 a≥b”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
【解析】(1)∵AE+BG=2CF,CF>DF,AE= 1
1n ,BG= 1
1n ,DF= 1
n ,
∴ 1
1n + 1
1n > 2
n .故答案为: 1
1n + 1
1n > 2
n .
(2)方法一:∵ 1
1n + 1
1n ﹣ 2
n =
2 2 22 2
( 1)( 1)
n n n n n
n n n
= 2
( 1)( 1)n n n ,
∵n>1,∴n(n﹣1)(n+1)>0,
∴ 1
1n + 1
1n ﹣ 2
n >0,∴ 1
1n + 1
1n > 2
n .
方法二:∵
1 1
1 1
2
n n
n
=
2
2 1
n
n >1,∴ 1
1n + 1
1n > 2
n .
【名师点睛】本题考查反比例函数图形上的点的坐标特征,反比例函数的图象等知识,解题的
关键是理解题意,灵活运用所学知识解决问题.
【变式 3-2】定义:如图,若双曲线 ky k 0x > 与它的其中一条对称轴 y x 相交于两点 A,B,
则线段 AB 的长称为双曲线 ky k 0x > 的对径.
(1)求双曲线 1y x
的对径;
(2)若某双曲线 ky k 0x > 对径是10 2 .求 k 的值;
(3)仿照上述定义,请你定义双曲线 ky k 0x < 的对径.
【答案】(1)2 2 ;(2)25;(3)定义见解析.
【解析】
试题分析:过 A 点作 AC⊥x 轴于 C,(1)解方程组
ky= x
y=x
,可得到 A 点坐标为(1,1),B 点
坐标为(-1,-1),即 OC=AC=1,由勾股定理可求 AB,于是得到双曲线 1y= x 的对径;
(2)根据双曲线的对径的定义得到当双曲线的对径为10 2 ,即 AB=10 2 ,OA=5 2 ,根
据 OA= 2 OC= 2 AC,则 OC=AC=5,得到点 A 坐标为(5,5),把 A(5,5)代入双曲线
ky= x (k>0)即可得到 k 的值;(3)双曲线 ky= x (k<0)的一条对称轴与双曲线有两个交点,根
据题目中的定义易得到双曲线 ky= x (k<0)的对径.
试题解析:如图,过 A 点作 AC⊥x 轴于 C,
(1)解方程组
ky= x
y=x
,得 1 2
1 2
x =1 x = 1
y =1 y = 1
, ,∴A 点坐标为(1,1),B 点坐标为(-1,-1).
∴OC=AC=1,∴OA= 2 OC= 2 . ∴AB=2OA=2 2 .
∴双曲线 1y= x 的对径是 2 2 .
(2)∵双曲线的对径为10 2 ,即 AB=10 2 ,OA=5 2 .
∴OA= 2 OC= 2 AC,∴OC=AC=5. ∴点 A 坐标为(5,5).
把 A(5,5)代入双曲线 ky= x (k>0)得 k=5×5=25,即 k 的值为 25.
(3)若双曲线 ky= x (k<0)与它的其中一条对称轴 y=-x 相交于 A、B 两点,则线段 AB 的长
称为双曲线 ky= x (k<0)的对径.
考点:1.新定义;2.反比例函数综合题;3.曲线上点的坐标与方程的关系;4.勾股定理.
【考点 4】变换操作类阅读型问题
【例 4】.我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,
则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊的四边形中是勾股四边形的两种图形的名称 、 ;
(2)如图 1,已知格点(小正方形的顶点)O0,0、A3,0、B0,4,点 C 为图中所给方格中的
另一个格点,四边形 OACB 是以 OA 、OB 为勾股边且对角线相等的勾股四边形,求点 C 的
坐标;
(3)如图 2,将ABC( BC AB )绕顶点 B 按顺时针方向旋转 60,得到DBE ,连接 AD 、
DC ,四边形 ABCD 是勾股四边形,其中 DC 、BC 为勾股边,求DCB 的度数.
【答案】(1)矩形,正方形(答案不唯一);(2)C(3,4),(4,3);(3)∠DCB=30°.
【解析】
【分析】
(1)根据矩形与正方形的性质可得答案;
(2)利用勾股定理可得 AB=5,然后在格点中找满足 OC=5 的点即可;
(3)连接 CE,根据旋转的性质可得△ABC≌△DBE,则 BC=BE,因为∠CBE=60°,所以
△BCE 是等边三角形,则 BC=CE,∠BCE=60°,根据勾股四边形的定义与勾股定理的逆定
理可得∠DCE=90°,则可得∠DCB 的度数.
【详解】
解:(1)矩形;正方形(答案不唯一);
(2) ,
则 C 点坐标如图为:(3,4),(4,3);
(3)连接 CE,
由旋转的性质得:△ABC≌△DBE,则 BC=BE,AC=BD,
∵∠CBE=60°,
∴△BCE 是等边三角形,
∴BC=CE,∠BCE=60°,
∵四边形 ABCD 为勾股四边形,其中 DC、BC 为勾股边,
∴ ,
∴ ,
∴∠DCE=90°,
∴∠BCD=∠DCE﹣∠BCE=90°﹣60°=30°.
【点睛】
本题主要考查勾股定理及其逆定理,全等三角形-旋转,等边三角形的判定等,解此题的关键
在于准确理解题中勾股四边形的定义,利用勾股定理及其逆定理进行证明.与计算.
【变式 4-1】1.类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻
边四边形”.
(1) 概念理解:
如图 1,在四边形 ABCD中,添加一个条件,使得四边形 ABCD是“等邻边四边形”,请写出
你添加的一个条件: .
(2) 问题探究:
如图 2,小红画了一个 ABCRt ,其中 90ABC , 2AB , 1BC ,并将 ABCRt 沿 B 的
平分线 BB 方向平移得到 ''' CBA ,连结 AA 、 BC .小红要使平移后的四边形 ABC A 是“等
邻边四边形”,应平移多少距离(即线段 BB 的长)?
(3) 应用拓展:
如图 3,“等邻边四边形” ABCD中, AB AD , 90BAD BCD , AC 、BD 为对角线,
2AC AB .试探究 BC 、CD、 BD 的数量关系.
【答案】(1)DA=AB(答案不唯一);(2)应平移 2 或 5 或 2 或 14 2
2
的距离;(3)
BC2+CD2=2BD2.
【解析】
试题分析:(1)由“等邻边四边形”的定义易得出结论;
(2)①先利用平行四边形的判定定理得平行四边形,再利用“等邻边四边形”定义得邻边相
等,得出结论;
② 由 平 移 的 性 质 易 得 BB′=AA′ , A′B′ ∥ AB , A′B′=AB=2 , B′C′=BC=1 ,
A′C′=AC= ,再利用“等邻边四边形”定义分类讨论,由勾股定理得出结论;
(3)由旋转的性质可得△ABF≌△ADC,由全等性质得∠ABF=∠ADC,∠BAF=∠DAC,
AF=AC,FB=CD,利用相似三角形判定得△ACF∽△ABD,由相似的性质和四边形内角和得
∠CBF=90°,利用勾股定理,等量代换得出结论.
解:(1)AB=BC 或 BC=CD 或 CD=AD 或 AD=AB(任写一个即可);
(2)①正确,理由为:
∵四边形的对角线互相平分,∴这个四边形是平行四边形,
∵四边形是“等邻边四边形”,∴这个四边形有一组邻边相等,
∴这个“等邻边四边形”是菱形;
②∵∠ABC=90°,AB=2,BC=1,
∴AC= ,
∵将 Rt△ABC 平移得到△A′B′C′,
∴BB′=AA′,A′B′∥AB,A′B′=AB=2,B′C′=BC=1,A′C′=AC= ,
(I)如图 1,当 AA′=AB 时,BB′=AA′=AB=2;
(II)如图 2,当 AA′=A′C′时,BB′=AA′=A′C′= ;
(III)当 A′C′=BC′= 时,
如图 3,延长 C′B′交 AB 于点 D,则 C′B′⊥AB,
∵BB′平分∠ABC,
∴∠ABB′= ∠ABC=45°,
∴∠BB′D=′∠ABB′=45°
∴B′D=B,
设 B′D=BD=x,
则 C′D=x+1,BB′= x,
∵在 Rt△BC′D 中,BD2+(C′D)2=(BC′)2
∴x2+(x+1)2=( )2,
解得:x1=1,x2=﹣2(不合题意,舍去),
∴BB′= x=
(Ⅳ)当 BC′=AB=2 时,如图 4,与(Ⅲ)方法一同理可得:BD2+(C′D)2=(BC′)2,
设 B′D=BD=x,
则 x2+(x+1)2=22,
解得:x1= ,x2= (不合题意,舍去),
∴BB′= x= ;
(3)BC,CD,BD 的数量关系为:BC2+CD2=2BD2,如图 5,
∵AB=AD,
∴将△ADC 绕点 A 旋转到△ABF,连接 CF,
∴△ABF≌△ADC,
∴∠ABF=∠ADC,∠BAF=∠DAC,AF=AC,FB=CD,
∴∠BAD=∠CAF, = =1,
∴△ACF∽△ABD,
∴ = = ,∴ BD,
∵∠BAD+∠ADC+∠BCD+∠ABC=360°,
∴∠ABC+∠ADC﹣360°﹣(∠BAD+∠BCD)=360°﹣90°=270°,
∴∠ABC+∠ABF=270°,
∴∠CBF=90°,
∴BC2+FB2=CF2=( BD)2=2BD2,
∴BC2+CD2=2BD2.
考点:1.阅读理解题;2.平移,旋转的图形变换性质;3.三角形全等、相似的判定与性质;
4.勾股定理的运用.
【变式 4-2】(2019•湖南长沙)根据相似多边形的定义,我们把四个角分别相等,四条边成
比例的两个凸四边形叫做相似四边形.相似四边形对应边的比叫做相似比.
(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在
横线上填写“真”或“假”).
①四条边成比例的两个凸四边形相似;(__________命题)
②三个角分别相等的两个凸四边形相似;(__________命题)
③两个大小不同的正方形相似.(__________命题)
(2)如图 1,在四边形 ABCD 和四边形 A1B1C1D1 中,∠ABC=∠A1B1C1,∠BCD=∠B1C1D1,
1 1
AB
A B =
1 1
BC
B C =
1 1
CD
C D .求证:四边形 ABCD 与四边形 A1B1C1D1 相似.
(3)如图 2,四边形 ABCD 中,AB∥CD,AC 与 BD 相交于点 O,过点 O 作 EF∥AB 分别
交 AD,BC 于点 E,F.记四边形 ABFE 的面积为 S1,四边形 EFCD 的面积为 S2,若四边形
ABFE 与四边形 EFCD 相似,求 2
1
S
S 的值.
【解析】(1)①四条边成比例的两个凸四边形相似,是假命题,角不一定相等.
②三个角分别相等的两个凸四边形相似,是假命题,边不一定成比例.
③两个大小不同的正方形相似.是真命题.
故答案为假,假,真.
(2)如图 1 中,连接 BD,B1D1.
∵∠BCD=∠B1C1D1,且
1 1
BC
B C =
1 1
CD
C D ,
∴△BCD∽△B1C1D1,∴∠CDB=∠C1D1B1,∠C1B1D1=∠CBD,
∵
1 1
AB
A B =
1 1
BC
B C =
1 1
CD
C D ,∴
1 1
BD
B D =
1 1
AB
A B ,
∵∠ABC=∠A1B1C1,∴∠ABD=∠A1B1D1,∴△ABD∽△A1B1D1,
∴
1 1
AD
A D =
1 1
AB
A B ,∠A=∠A1,∠ADB=∠A1D1B1,
∴
1 1
AB
A B =
1 1
BC
B C =
1 1
CD
C D =
1 1
AD
A D ,∠ADC=∠A1D1C1,∠A=∠A1,∠ABC=∠A1B1C1,∠BCD=
∠B1C1D1,
∴四边形 ABCD 与四边形 A1B1C1D1 相似.
(3)如图 2 中,
∵四边形 ABCD 与四边形 EFCD 相似,∴ DE
AE = EF
AB ,
∵EF=OE+OF,∴ DE
AE = OE OF
AB
,
∵EF∥AB∥CD,∴ DE
AD = OE
AB , DE OC OF
AD AB AB
,
∴ DE
AD + DE
AD = OE
AB + OF
AB ,∴ 2DE
AD = DE
AE ,
∵AD=DE+AE,∴ 2
DE AE = 1
AE ,
∴2AE=DE+AE,∴AE=DE,
∴ 2
1
S
S =1.
【名师点睛】本题属于相似形综合题,考查了相似三角形的判定和性质,相似多边形的判定和
性质等知识,解题的关键是学会用转化的思想思考问题,属于中考压轴题.
1.(2019•湘西州)阅读材料:设 a =(x1,y1),b
=(x2,y2),如果 a ∥b
,则 x1•y2=x2
•y1,根据该材料填空,已知 a =(4,3),b
=(8,m),且 a ∥b
,则 m=__________.
【答案】6
【解析】∵ a =(4,3),b
=(8,m),且 a ∥b
,∴4m=3×8,∴m=6;故答案为:6.
【名师点睛】本题考查新定义,点的坐标;理解阅读材料的内容,转化为所学知识求解是关键.
2.(2019•白银)定义:等腰三角形的顶角与其一个底角的度数的比值 k 称为这个等腰三角
形的“特征值”.若等腰△ABC 中,∠A=80°,则它的特征值 k=__________.
【答案】 8
5 或 1
4
【解析】①当∠A 为顶角时,等腰三角形两底角的度数为: 2
180 80 =50°,
∴特征值 k= 80 8
50 5
;
②当∠A 为底角时,顶角的度数为:180°–80°–80°=20°,
∴特征值 k= 20
80
1
4
;
综上所述,特征值 k 为 8
5 或 1
4 ;
故答案为 8
5 或 1
4 .
【名师点睛】本题主要考查等腰三角形的性质,熟记等腰三角形的性质是解题的关键,要注意
到本题中,已知∠A 的底数,要进行判断是底角或顶角,以免造成答案的遗漏.
3.我们定义:对于抛物线 2 0y ax bx c a ,以 y 轴上的点 0,M m 为中心,作该抛物线关于
点 M 对称的抛物线 'y ,则我们又称抛物线 'y 为抛物线 y 的“衍生抛物线”,点 M 为“衍生中
心”,若抛物线 2 2 5y x x 关于点 0,m 的衍生抛物线为 'y ,若这两条抛物线有交点,则 m
的取值范围是______.
【答案】m≤5
【解析】
【分析】
先求出抛物线的顶点坐标(-1,6),进而利用待定系数法求出衍生抛物线的解析式,联立即可
得出结论;
【详解】
解∵抛物线 y=-x2-2x+5=-(x+1)2+6①,
∴抛物线的顶点坐标为(-1,6),
∴抛物线的顶点坐标(-1,6)关于(0,m)的对称点为(1,2m-6),
即:新抛物线的顶点坐标为(1,2m-6),
设衍生抛物线为 y′=a(x-1)2+2m-6,
∵抛物线 y=-x2-2x+5 关于点(0,m)的衍生抛物线为 y′,
∴a=1,
∴衍生抛物线为 y′=(x-1)2+2m-6=x2-2x+2m-5②,
联立①②得,x2-2x+2m-5=-x2-2x+5,
整理得,2x2=10-2m,
∵这两条抛物线有交点,
∴10-2m≥0,
∴m≤5;
【点睛】
此题主要考查了待定系数法,抛物线顶点坐标的求法,新定义的理解和掌握,点的对称点坐标
的求法,理解新定义是解本题的关键.
4.(2019•河北)如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
示例: 即 4+3=7.
则(1)用含 x 的式子表示 m=__________;
(2)当 y=–2 时,n 的值为__________.
【答案】(1)3x;(2)1.
【解析】(1)根据约定的方法可得:m=x+2x=3x;故答案为:3x;
(2)根据约定的方法即可得 x+2x+2x+3=m+n=y.
当 y=–2 时,5x+3=–2.
解得 x=–1.
∴n=2x+3=–2+3=1.
故答案为:1.
【名师点睛】本题考查了列代数式和代数式求值,解题的关键是掌握列代数式的约定方法.
5.(2019•湖北宜昌•3 分)古希腊几何学家海伦和我国宋代数学家秦九韶都曾提出利用三角形
的三边求面积的公式,称为海伦﹣秦九韶公式:如果一个三角形的三边长分别是 a,b,c,
记 p= 2
a b c ,那么三角形的面积为 S= ( )( )( )p p a p b p c .如图,在△ABC 中,∠A,
∠B,∠C 所对的边分别记为 a,b,c,若 a=5,b=6,c=7,则△ABC 的面积为
A.6 6 B.6 3 C.18 D.19
2
【答案】A
【解析】∵a=7,b=5,c=6,∴p= 5 6 7
2
=9,
∴△ABC 的面积 S= 9 (9 5) (9 6) (9 7) =6 6 .故选 A.
【名师点睛】考查了二次根式的化简,解题的关键是代入后正确的运算,难度不大.
6.(2019•山东临沂)一般地,如果 x4=a(a≥0),则称 x 为 a 的四次方根,一个正数 a 的
四次方根有两个.它们互为相反数,记为± 4 a ,若 44 m =10,则 m=__________.
【答案】±10
【解析】∵ 44 m =10,∴m4=104,∴m=±10.故答案为:±10.
【名师点睛】本题考查了方根的定义.关键是求四次方根时,注意正数的四次方根有 2 个.
7.(2019•湖北十堰)对于实数 a,b,定义运算“◎”如下:a◎b=(a+b)2﹣(a﹣b)2.若
(m+2)◎(m﹣3)=24,则 m=__________.
【答案】﹣3 或 4
【解析】根据题意得[(m+2)+(m﹣3)]2﹣[(m+2)﹣(m﹣3)]2=24,
(2m﹣1)2﹣49=0,
(2m﹣1+7)(2m﹣1﹣7)=0,
2m﹣1+7=0 或 2m﹣1﹣7=0,
所以 m1=﹣3,m2=4.
故答案为:﹣3 或 4.
【名师点睛】本题考查了解一元二次方程﹣因式分解法:因式分解法就是利用因式分解求出方
程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.
4.8.据规定判断下面四个结论:①正方形和菱形都是广义菱形;②平行四边形是广义菱形;
③对角线互相垂直,且两组邻边分别相等的四边形是广义菱形;④若 M、N 的坐标分别为(0,
1),(0,-1),P 是二次函数 y= 4
1 x2 的图象上在第一象限内的任意一点,PQ 垂直直线 y=
-1 于点 Q,则四边形 PMNQ 是广义菱形.其中正确的是__________.(填序号)
【答案】①④
【解析】①根据广义菱形的定义,正方形和菱形都有一组对边平行,一组邻边相等,①正确;
②平行四边形有一组对边平行,没有一组邻边相等,②错误;
③由给出条件无法得到一组对边平行,③错误;
④设点 P(m,1
4 m2),则 Q(m,-1),∴MP= 2 2 21( 1)4m m =| 1
4 m2+1|,PQ= 1
4 m2+1,
∵点 P 在第一象限,∴m>0,∴MP= 1
4 m2+1,∴MP=PQ,
又∵MN∥PQ,∴四边形 PMNQ 是广义菱形.④正确.
故答案为:①④.
【名师点睛】本题考查新定义,二次函数的性质,特殊四边形的性质;熟练掌握平行四边形,
菱形,二次函数的图象及性质,将广义菱形的性质转化为已学知识是求解的关键.
9.(2019•浙江湖州)七巧板是我国祖先的一项卓越创造,被誉为“东方魔板”.由边长为 4
的正方形 ABCD 可以制作一副如图 1 所示的七巧板,现将这副七巧板在正方形 EFGH 内拼成
如图 2 所示的“拼搏兔”造型(其中点 Q、R 分别与图 2 中的点 E、G 重合,点 P 在边 EH 上),
则“拼搏兔”所在正方形 EFGH 的边长是__________.
【答案】4 5
【解析】如图 2 中,连接 EG,作 GM⊥EN 交 EN 的延长线于 M.
在 Rt△EMG 中,∵GM=4,EM=2+2+4+4=12,
∴EG= 2 2EM GM = 2 212 4 =4 10 ,
∴EH= 2
EG =4 5 ,故答案为:4 5 .
【名师点睛】本题考查正方形的性质,七巧板,勾股定理等知识,解题的关键是学会添加常用
辅助线,构造直角三角形解决问题.
10(2019•广西贵港)我们定义一种新函数:形如 y=|ax2+bx+c|(a≠0,且 b2﹣4a>0)的
函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数 y=|x2﹣2x﹣3|的图象(如图所示),
并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象
具有对称性,对称轴是直线 x=1;③当﹣1≤x≤1 或 x≥3 时,函数值 y 随 x 值的增大而增大;
④当 x=﹣1 或 x=3 时,函数的最小值是 0;⑤当 x=1 时,函数的最大值是 4.其中正确结论的
个数是__________.
【答案】4
【解析】①∵(﹣1,0),(3,0)和(0,3)坐标都满足函数 y=|x2﹣2x﹣3|,∴①是正
确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线 x=1,因此②也是正确的;
③根据函数的图象和性质,发现当﹣1≤x≤1 或 x≥3 时,函数值 y 随 x 值的增大而增大,因
此③也是正确的;
④函数图象的最低点就是与 x 轴的两个交点,根据 y=0,求出相应的 x 的值为 x=﹣1 或 x=3,
因此④也是正确的;
⑤从图象上看,当 x<﹣1 或 x>3,函数值要大于当 x=1 时的 y=|x2﹣2x﹣3|=4,因此⑤时不
正确的;
故答案是:4.
【名师点睛】理解“鹊桥”函数 y=|ax2+bx+c|的意义,掌握“鹊桥”函数与 y=|ax2+bx+c|
与二次函数 y=ax2+bx+c 之间的关系;两个函数性质之间的联系和区别是解决问题的关键;
二次函数 y=ax2+bx+c 与 x 轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握.
11.(2019·贵州安顺)阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔(J.Nplcr,1550﹣1617 年),纳皮尔发明对数是在指
数书写方式之前,直到 18 世纪瑞士数学家欧拉(Evlcr,1707﹣1783 年)才发现指数与对数
之间的联系.
对数的定义:一般地,若 ax=N(a>0 且 a≠1),那么 x 叫做以 a 为底 N 的对数,记作 x=logaN,
比如指数式 24=16 可以转化为对数式 4=log216,对数式 2=log525,可以转化为指数式 52=25.
我们根据对数的定义可得到对数的一个性质:
loga(M•N)=logaM+logaN(a>0,a≠1,M>0,N>0),理由如下:
设 logaM=m,logaN=n,则 M=am,N=an,
∴M•N=am•an=am+n,由对数的定义得 m+n=loga(M•N)
又∵m+n=logaM+logaN
∴loga(M•N)=logaM+logaN
根据阅读材料,解决以下问题:
(1)将指数式 34=81 转化为对数式;
(2)求证:loga
M
N =logaM﹣logaN(a>0,a≠1,M>0,N>0)
(3)拓展运用:计算 log69+log68﹣log62=.
【解析】(1)4=log381(或 log381=4),故答案为:4=log381;
(2)证明:设 logaM=m,logaN=n,则 M=am,N=an,
∴ M
N =
m
n
a
a
=am﹣n,由对数的定义得 m﹣n=loga
M
N ,
又∵m﹣n=logaM﹣logaN,∴loga
M
N =logaM﹣logaN;
(3)log69+log68﹣log62=log6(9×8÷2)=log636=2.
故答案为:2.
12.定义:有一个角是其对角两倍的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.已
知四边形 ABCD 是圆美四边形
1 求美角 C 的度数;
2 如图 1,若 O 的半径为 2 3 ,求 BD 的长;
3 如图 2,若 CA 平分 BCD ,求证: BC CD AC .
【答案】(1)120°;(2)6;(3)见解析.
【解析】
【分析】
1 先判断出 2C A ,再判断出 180A C ,即可得出结论;
2 先求出 60E ,再求出 DE,最后用锐角三角函数即可得出结论;
3 作出辅助线,判断出 BCF 是等边三角形,得出 AFB BCD ,进而判断出
ABF ≌ DBC ,得出 CAF D ,即可得出结论.
【详解】
解: 1 四边形 ABCD 是圆美四边形,
C 2 A ,
四边形 ABCD 是圆内接四边形,
A C 180 ,
A 2 A 180 ,
A 60 ,
C 120 ;
2 由 1 知, A 60 ,
如图 1,连接 DO 并延长交 O 于 E,连接 BE,
E A 60 ,
O 的半径为 2 3 ,
DE 2 2 3 4 3 ,
在 Rt DBE中, 3BD DE sinE 4 3 62
;
3 如图 2,在 CA 上截取CF CB ,
由 1 知, BCD 120 ,
CA 平分 BCD ,
1BCA ACD BCD 602
,
BCF 是等边三角形,
BC BF , BFC 60 ,
AFB 120 , AFB BCD ,
在 ABF 和 BCD 中,
BAF BDC
AFB BCD
BF BC
,
ABF ≌ DBC AAS ,
AF DC ,
AC CF AF BC CD .
【点睛】
此题是圆的综合题,主要考查了圆周角定理,锐角三角函数,等边三角形的判定和性质,全等
三角形的判定和性质,正确作出辅助线是解本题的关键.
13.(2019•枣庄)对于实数 a、b,定义关于“⊗”的一种运算:a⊗b=2a+b,例如 3⊗4=2
×3+4=10.
(1)求 4⊗(–3)的值;
(2)若 x⊗(–y)=2,(2y)⊗x=–1,求 x+y 的值.
【答案】(1)5;(2) 1
3 .
【解析】(1)根据题中的新定义得:原式=8–3=5;
(2)根据题中的新定义化简得: 2 2
4 1
x y
x y
①
② ,
①+②得:3x+3y=1,则 x+y= 1
3 .
【名师点睛】此题考查了解二元一次方程组,以及实数的运算,熟练掌握运算法则是解本题的
关键.
14.在课外活动中,我们要研究一种凹四边形——燕尾四边形的性质.
定义 1:把四边形的某些边向两方延长,其他各边有不在延长所得直线的同一旁,这样的四边
形叫做凹四边形(如图 1).
(1)根据凹四边形的定义,下列四边形是凹四边形的是(填写序号) ;
① ② ③
定义 2:两组邻边分别相等的凹四边形叫做燕尾四边形(如图 2).
特别地,有三边相等的凹四边形不属于燕尾四边形.
小洁根据学习平行四边形、菱形、矩形、正方形的经验,对燕尾四边形的性质进行了探究.
下面是小洁的探究过程,请补充完整:
(2)通过观察、测量、折叠等操作活动,写出两条对燕尾四边形性质的猜想,并选取其中的
一条猜想加以证明;
(3)如图 2,在燕尾四边形 ABCD 中,AB=AD=6,BC=DC=4,∠BCD=120°,求燕尾四
边形 ABCD 的面积(直接写出结果).
【答案】(1)①;(2)答案见解析;(3)12 2 4 3
【解析】
试题分析:(1)根据凹四边形的定义即可得出结论;
(2)由燕尾四边形的定义可以得出燕尾四边形的性质;
(3)连接 BD,根据 SΔABD-SΔBCD 即可求出燕尾四边形 ABCD 的面积.
试题解析:(1)①.
(2)它是一个轴对称图形;两组邻边分别相等;一组对角相等;一条对角线所在的直线垂直
平分另一条对角线等等.
已知:如图,在凹四边形 ABCD 中,AB=AD,BC=DC.
求证:∠B=∠D.
证明:连接 AC.
∵AB=AD,CB=CD,AC=AC,
∴△ABC≌△ADC.
∴∠B=∠D.
(3)燕尾四边形 ABCD 的面积为12 2 4 3 .
15.定义:对角线互相垂直的圆内接四边形叫做圆的奇妙四边形.
(1)如图①,已知四边形 ABCD是⊙O的奇妙四边形,若 6AC , 8BD 则
ABCDS =四边形 _______;
(2)如图②,已知四边形 ABCD内接于⊙O,对角线交于点 E ,若 m
AD BC 180 ,
①求证:四边形 ABCD是⊙O的奇妙四边形;
②作OM BC 于 M ,请猜想 AD 与OM 之间的数量关系,并推理说明.
【答案】(1)24;(2)①见解析,② 2AD OM 或 1 2OM AD ,见解析.
【解析】
【分析】
(1)由 ABCDS四边形 =S△ADC+S△ABC= 1
2 AC·BD 即可得到答案.
(2)①证:四边形 ABCD是⊙O的奇妙四边形,证 AC BD 即可.
②过点O作OM BC ,垂足为点 M , 20MAD 分不同情况证明 或 1/ 2OM AD .
【详解】
解:(1) 24S
ABCDS四边形 =S△ADC+S△ABC= 1
2 AC·BD= 1
2 ×6×8=24
(2)如图,由题得, 1
2
mABD AD
, 1
2
mBAE BC
180
m
AD BC
90ABD BAE
90AEB
AC BD
四边形是 ABCD的⊙O奇妙四边形.
②如图,过点O作OM BC ,垂足为点 M , AD 与OM 之间的数量关系: 20MAD 或
1/ 2OM AD
图②
推理说明如下:
解法一:
如图③,连结并延长 BO交⊙O于点 N ,连结CN
图③
OM BC 为 BC 的中点
又 O 为 BN 的中点
OM 是 BCN 的中位线
1/ 2OM CN
BN 为直径
90BCN 即 90NBC BNC
BAC BNC
ABD NBC (等角的余角相等)
AD CN
1/ 2OM AD
解法二:
如图③,连结OA、OB 、OC 、OD ,过点O作ON AD 于点 N ,
OM BC ,ON AD
90OMC OND , 1/ 2NOD AOD , 1/ 2COM COB
1/ 2COM COB
m
AD BC 180 180AOD COB
90NOD COM OCM NOD
OC OD COM ODN
OM DN
又 2ON AD AD DN
20MAD
【点睛】
本题考查的知识点是新情境下圆的应用,解题的关键是熟练的掌握新情境下圆的应用.
16.定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
1 如图 1,点 A B C, , 在 O 上, ABC 的平分线交 O 于点 D ,连接 AD CD, .求证:四边
形 ABCD是等补四边形;
探究:
2 如图 2,在等补四边形 ABCD中 AB AD, = ,连接 AC AC, 是否平分 ?BCD 请说明理由.
运用:
3 如图 3,在等补四边形 ABCD中, AB AD= ,其外角 EAD 的平分线交CD 的延长线于点
10 5F CD AF, = , = ,求 DF 的长.
【答案】(1)证明见解析;(2) AD 平分 BCD ,理由见解析;(3) 5 2 5DF= ﹣..
【解析】
【分析】
1 由圆内接四边形互补可知 180 180A C ABC ADC = , = ,再证 AD CD= ,即可根据
等补四边形的定义得出结论;
2 过点 A分别作 AE BC 于点 E , AF 垂直CD 的延长线于点 F ,证 ABE ADF△ ≌△ ,得到
AE AF= ,根据角平分线的判定可得出结论;
3 连接 AC ,先证 EAD BCD = ,推出 FCA FAD = ,再证 ACF DAF∽ ,利用相似三角形对
应边的比相等可求出 DF 的长.
【详解】
1 证明:四边形 ABCD为圆内接四边形,
180 180A C ABC ADC = , = ,
BD ABC 平分 ,
ABD CBD = ,
AD CD
AD CD = ,
四边形 ABCD是等补四边形;
2 AD 平分 BCD ,理由如下:
如图 2,过点 A分别作 AE BC 于点 E ,AF 垂直CD 的延长线于点 F ,则 90AEB AFD = = ,
四边形 ABCD是等补四边形,
180B ADC = ,
又 180ADC ADF = ,
B ADF = ,
AB AD = ,
ABE ADF AAS ≌ ( ),
AE AF = ,
AC 是 BCF 的平分线,即 AC 平分 BCD ;
3 如图 3,连接 AC ,
四边形 ABCD是等补四边形,
180BAD BCD = ,
又 180BAD EAD = ,
EAD BCD = ,
AF 平分 EAD ,
1
2FAD EAD = ,
由 2 知, AC 平分 BCD ,
1
2FCA BCD
FCA FAD = ,
又 AFC DFA = ,
ACF DAF ∽ ,
AF CF
DF AF
即 5 10
5
DF
DF
5 2 5DF = ﹣.
【点睛】
本题考查了新定义等补四边形,圆的有关性质,全等三角形的判定与性质,角平分线的判定,
相似三角形的判定与性质等,解题关键是要能够通过自主学习来进行探究,运用等.
17.定义:有一组邻边相等的凸四边形叫做“准菱形”,利用该定义完成以下各题:
(1)理解:如图 1,在四边形 ABCD 中,若__________(填一种情况),则四边形 ABCD 是
“准菱形”;
(2)应用:证明:对角线相等且互相平分的“准菱形”是正方形;(请画出图形,写出已知,
求证并证明)
(3)拓展:如图 2,在 Rt△ABC 中,∠ABC=90°,AB=2,BC=1,将 Rt△ABC 沿∠ABC
的平分线 BP 方向平移得到△DEF,连接 AD,BF,若平移后的四边形 ABFD 是“准菱形”,
求线段 BE 的长.
【答案】(1)答案不唯一,如 AB=BC.(2)见解析;(3) BE=2 或 5 或 2 或 14 2
2
.
【解析】
整体分析:
(1)根据“准菱形”的定义解答,答案不唯一;(2)对角线相等且互相平分的四边形是矩形,矩
形的邻边相等时即是正方形;(3)根据平移的性质和“准菱形”的定义,分四种情况画出图形,
结合勾股定理求解.
解:(1)答案不唯一,如 AB=BC.
(2)已知:四边形 ABCD 是“准菱形”,AB=BC,对角线 AC,BO 交于点 O,且 AC=BD,
OA=OC,OB=OD.
求证:四边形 ABCD 是正方形.
证明:∵OA=OC,OB=OD,
∴四边形 ABCD 是平行四边形.
∵AC=BD,
∴平行四边形 ABCD 是矩形.
∵四边形 ABCD 是“准菱形”,AB=BC,
∴四边形 ABCD 是正方形.
(3)由平移得 BE=AD,DE=AB=2,EF=BC=1,DF=AC= 5 .
由“准菱形”的定义有四种情况:
①如图 1,当 AD=AB 时,BE=AD=AB=2.
②如图 2,当 AD=DF 时,BE=AD=DF= 5 .
③如图 3,当 BF=DF= 5 时,延长 FE 交 AB 于点 H,则 FH⊥AB.
∵BE 平分∠ABC,∴∠ABE= 1
2 ∠ABC=45°.
∴∠BEH=∠ABE=45°.∴BE= 2 BH.
设 EH=BH=x,则 FH=x+1,BE= 2 x.
∵在 Rt△BFH 中,BH2+FH2=BF2,
∴x2+(x+1)2=( 5 )2,
解得 x1=1,x2=-2(不合题意,舍去),
∴BE= 2 x= 2 .
④如图 4,当 BF=AB=2 时,与③)同理得:BH2+FH2=BF2.
设 EH=BH=x,则 x2+(x+1)2=22,
解得 x1= 1 7
2
,x2= 1 7
2
(不合题意,舍去),
∴BE= 2 x= 14 2
2
.
综上所述,BE=2 或 5 或 2 或 14 2
2
.
18.定义:有且仅有一组对角相等的凸四边形叫做“准平行四边形”.例如:凸四边形 ABCD中,
若 ,A C B D ,则称四边形 ABCD为准平行四边形.
(1)如图①, , , ,A P B C 是 O 上的四个点, 60APC CPB ,延长 BP 到Q ,使 AQ AP .
求证:四边形 AQBC 是准平行四边形;
(2)如图②,准平行四边形 ABCD内接于 O , ,AB AD BC DC ,若 O 的半径为5, 6AB ,
求 AC 的长;
(3)如图③,在 Rt ABC 中, 90 , 30 , 2C A BC ,若四边形 ABCD是准平行四边形,
且 BCD BAD ,请直接写出 BD 长的最大值.
【答案】(1)见解析;(2)7 2 ;(3) 2 3 2
【解析】
【分析】
(1)先根据同弧所对的圆周角相等证明三角形 ABC 为等边三角形,得到∠ACB=60°,再求
出∠APB=60°,根据 AQ=AP 判定△APQ 为等边三角形,∠AQP=∠QAP=60°,故
∠ACB=∠AQP,可判断∠QAC>120°,∠QBC<120°,故∠QAC≠∠QBC,可证四边
形 AQBC 是准平行四边形;
(2)根据已知条件可判断∠ABC≠∠ADC,则可得∠BAD=∠BCD=90°,连接 BD,则 BD
为直径为 10,根据 BC=CD 得△BCD 为等腰直角三角形,则∠BAC=∠BDC=45°,在直角
三角形 BCD 中利用勾股定理或三角函数求出 BC 的长,过 B 点作 BE⊥AC,分别在直角三角
形 ABE 和△BEC 中,利用三角函数和勾股定理求出 AE、CE 的长,即可求出 AC 的长.
(3)根据已知条件可得:∠ADC=∠ABC=60°,延长 BC 到 E 点,使 BE=BA,可得三角形
ABE 为等边三角形,∠E=60°,过 A、E、C 三点作圆 o,则 AE 为直径,点 D 在点 C 另一
侧的弧 AE 上(点 A、点 E 除外),连接 BO 交弧 AE 于 D 点,则此时 BD 的长度最大,根据已
知条件求出 BO、OD 的长度,即可求解.
【详解】
(1)∵ 60APC CPB
∴∠ABC=∠BAC=60°
∴△ABC 为等边三角形,∠ACB=60°
∵∠APQ=180°-∠APC-∠CPB=60°
又 AP=AQ
∴△APQ 为等边三角形
∴∠AQP=∠QAP=60°
∴∠ACB=∠AQP
∵∠QAC=∠QAP+∠PAB+∠BAC=120°+∠PAB>120°
故∠QBC=360°-∠AQP-∠ACB-∠QAC<120°
∴∠QAC≠∠QBC
∴四边形 AQBC 是准平行四边形
(2)连接 BD,过 B 点作 BE⊥AC 于 E 点
∵准平行四边形 ABCD内接于 O , , AB AD BC DC
∴∠ABC≠∠ADC,∠BAD=∠BCD
∵∠BAD+∠BCD=180°
∴∠BAD=∠BCD=90°
∴BD 为 O 的直径
∵ O 的半径为 5
∴BD=10
∵BC=CD,∠BCD=90°
∴∠CBD=∠BDC=45°
∴BC=BD sin∠BDC=10 2 =5 22 ,∠BAC=∠BDC=45°
∵BE⊥AC
∴∠BEA=∠BEC=90°
∴AE=ABsin∠BAC=6 2 =3 22
∵∠ABE=∠BAE=45°
∴BE=AE=3 2
在直角三角形 BEC 中,EC= 2 2 4 2BC BE
∴AC=AE+EC=7 2
(3)在 Rt ABC 中, 90 , 30 C A
∴∠ABC=60°
∵四边形 ABCD是准平行四边形,且 BCD BAD
∴∠ADC=∠ABC=60°
延长 BC 到 E 点,使 BE=BA,可得三角形 ABE 为等边三角形,∠E=60°,过 A、E、C 三点
作圆 o,因为∠ACE=90°,则 AE 为直径,点 D 在点 C 另一侧的弧 AE 上(点 A、点 E 除外),
此时,∠ADC=∠AEC=60°,连接 BO 交弧 AE 于 D 点,则此时 BD 的长度最大.
在等边三角形 ABE 中,∠ACB=90°,BC=2
∴AE=BE=2BC=4
∴OE=OA=OD=2
∴BO⊥AE
∴BO=BEsin∠E=4 3 =2 32
∴BD=BO+0D=2+ 2 3
即 BD 长的最大值为 2+ 2 3
【点睛】
本题考查的是新概念及圆的相关知识,理解新概念的含义、掌握圆的性质是解答的关键,本题
的难点在第(3)小问,考查的是与圆相关的最大值及最小值问题,把握其中的不变量作出圆
是关键.
19.阅读理解并解决问题:一般地,如果把一个图形绕着一个定点旋转一定角度 ( 小于
360)后,能够与原来的图形重合,那么这个图形叫做旋转对称图形,这个定点叫做旋转对
称中心. 叫做这个旋转对称图形的一个旋转角.请依据上述定义解答下列问题:
(1)请写出一个旋转对称图形,这个图形有一个旋转角是90.这个图形可以是______;
(2)为了美化环境,某中学需要在一块正六边形空地上分别种植六种不同的花草,现将这块
空地按下列要求分成六块:①分割后的整个图形必须既是轴对称图形又是旋转对称图形;②六
块图形的面积相同.请你按上述两个要求,分别在图中的三个正六边形中画出三种不同的分割
方法(只要求画图正确,不写作法).
【答案】(1)答案不唯一,例如正方形,正八边形,圆等;(2)答案不唯一,见解析
【解析】
【分析】
(1)答案不唯一,根据旋转对称图形的定义可知正方形,正八边形,圆等都可以;
(2)根据轴对称和旋转对称的定义可以得出答案,具体见详解图.
【详解】
解:
(1)答案不唯一,例如正方形,正八边形,圆等等.
(2)答案不唯一,如图所示:
【点睛】
本题考查的是旋转对称和轴对称知识点,解题关键在于读懂题意即可.
20.给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四
边形为勾股四边形.
(1)以下四边形中,是勾股四边形的为 .(填写序号即可)
①矩形;②有一个角为直角的任意凸四边形;③有一个角为 60°的菱形.
(2)如图,将△ABC 绕顶点 B 按顺时针方向旋转 60°得到△DBE,∠DCB=30°,连接 AD,
DC,CE.
①求证:△BCE 是等边三角形;
②求证:四边形 ABCD 是勾股四边形.
【答案】(1)①②;(2)①证明见解析,②证明见解析
【解析】
试题分析:(1)由勾股四边形的定义和特殊四边形的性质,则可得出;
(2)①由旋转的性质可知△ABC≌△DBE,从而可得 BC=BE,由∠CBE=60°可得△BCE 为
等边三角形;②由①可得∠BCE=60°,从而可知△DCE 是直角三角形,再利用勾股定理即可
解决问题.
试题解析:
(1)①如图,
∵四边形 ABCD 是矩形,
∴∠B=90°,
∴AB2+BC2=AC2,
即:矩形是勾股四边形,
②如图,
∵∠B=90°,
∴AB2+BC2=AC2,
即:由一个角为直角的四边形是勾股四边形,
③有一个角为 60°的菱形,邻边边中没有直角,所以不满足勾股四边形的定义,
故答案为①②,
(2)①∵△ABC 绕点 B 顺时针旋转了 60°到△DBE,
∴BC=BE,∠CBE=60°,
∵在△BCE 中,
BC=BE,∠CBE=60°
∴△BCE 是等边三角形.
②∵△BCE 是等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=90°,
在 Rt△DCE 中,有 DC2+CE2=DE2,
∵DE=AC,BC=CE,
∴DC2+BC2=AC2,
∴四边形 ABCD 是勾股四边形.
21.(2019·黔东南州)某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,
他们将其中某些材料摘录如下:
对于三个实,数 a,b,c,用 M{a,b,c}表示这三个数的平均数,用 min{a,b,c}表示这
三个数中最小的数,例如 M{1,2,9}=1 2 9
3
=4,min{1,2,–3}=–3,min(3,1,1}=1.请
结合上述材料,解决下列问题:
(1)①M{(–2)2,22,–22}=__________,
②min{sin30°,cos60°,tan45°}=__________;
(2)若 min(3–2x,1+3x,–5}=–5,则 x 的取值范围为__________;
(3)若 M{–2x,x2,3}=2,求 x 的值;
(4)如果 M{2,1+x,2x}=min{2,1+x,2x},求 x 的值.
【解析】(1)①M{(–2)2,22,–22}= 4
3 ,
②min{sin30°,cos60°,tan45°}= 1
2 ;
故答案为: 4
3 , 1
2 .
(2)∵min(3–2x,1+3x,–5}=–5,
∴
3 2 5
1 3 5
x
x
,解得–2≤x≤4,
故答案为–2≤x≤4.
(3)∵M{–2x,x2,3}=2,
∴
22 3
3
x x =2,
解得 x=–1 或 3.
(4)∵M{2,1+x,2x}=min{2,1+x,2x},
又∵ 2
3
1 2x x =x+1,∴
1 2
1 2
x
x x
,
解得 1≤x≤1,∴x=1.
【名师点睛】本题考查不等式组,平均数,最小值等知识,解题的关键是熟练掌握基本知识,
学会用转化的思想思考问题,属于中考常考题型.
22.定义:如图 1,抛物线 2y ax bx c ( 0a )与 x 轴交于 A, B 两点,点 P 在该抛物线
上( P 点与 A, B 两点不重合),如果 ABP 的三边满足 2 2 2AP BP AB ,则称点 P 为抛物线
2y ax bx c ( 0a )的勾股点.
(1)求证:点 (0, 1)M 是抛物线 2 1y x 的勾股点.
(2)如图 2,已知抛物线 2:C y ax bx ( 0a )与 x 轴交于 A,B 两点,点 (1, 3)P 是抛物
线C 的勾股点,求抛物线C 的函数表达式.
【答案】(1)见解析;(2)y= 23 4 3
3 3x x
【解析】
【分析】
(1)先解方程 x2-1=0 得抛物线与 x 轴的交点 A、B 的坐标为(-1,0),B(1,0),利用两点
间的距离公式可得到 AM2=2,BM2=2,AB2=22=4,则 AM2+BM2=AB2,根据题中定义可判断
点 M(0,-1)是抛物线 y=x2-1 的勾股点;
(2)作 PH⊥AB 于 H,如图 2,先利用 P 点坐标求出∠PAH=60°,再根据点 P(1, 3 )
是抛物线 C 的勾股点得到∠APB=90°,所以∠PBA=30°,然后计算出 BH 得到 B 点坐标,
于是可利用待定系数法求抛物线 C 的解析式.
【详解】
(1)如图所示:令 0y 得, 2 1 0x ,解得 1 21, 1x x
∴ ( 1,0)A , (1,0)B
∴ 1OA , 1OB , 2AB , 1OM
∴ 2 2 2 2 21 1 2AM OA OM
2 2 2 2 21 1 2BM OB OM
2 4AB
∴ 2 2 2AB AM BM
∴点 (0, 1)M 是抛物线 2 1y x 的勾股点.
(2)抛物线 2y ax bx 过原点,即点 (0,0)A
如图,作 PG x 轴于点G
∵点 P 的坐标为(1, 3)
∴ 1AG , 3PG , 2 2 2 21 ( 3) 2PA AG PG
∵点 (1, 3)P 是抛物线C 的勾股点
∴ 2 2 2AP BP AB
∴ PAB 是直角三角形
设 BG x
∵ 2 2 2 2AB AP PG BG
∴ 2 2 2 2(1 ) 2 ( 3)x x
∴ 3x
∴ 3GB
∴ 4AB
∴点 B 坐标为(4,0)
设 ( 4)y ax x
将点 (1, 3)P 代入得: 3
3a
∴ 23 3 4 3( 4)3 3 3y x x x x
【点睛】
本题考查了抛物线与 x 轴的交点:把求二次函数 y=ax2+bx+c(a,b,c 是常数,a≠0)与
x 轴的交点坐标问题转化为解关于 x 的一元二次方程.也考查了二次函数的性质和勾股定理.
23.定义:若抛物线 2
2 : 0L y mx nx m 与抛物线 2
1 : 0L y ax bx a 的开口大小相同,
方向相反,且抛物线 2L 经过 1L 的顶点,我们称抛物线 2L 为 1L 的“友好抛物线”.
(1)若 1L 的表达式为 2 2y x x ,求 1L 的“友好抛物线”的表达式;
(2)已知抛物线 2
2 :L y mx nx 为 2
1 :L y ax bx 的“友好抛物线”.求证:抛物线 1L 也是 2L
的“友好抛物线”;
(3)平面上有点 1,0P , 3,0Q ,抛物线 2
2 :L y mx nx 为 2
1 :L y ax 的“友好抛物线”,
且抛物线 2L 的顶点在第一象限,纵坐标为 2,当抛物线 2L 与线段 PQ 没有公共点时,求 a 的取
值范围.
【答案】(1) 1L 的“友好抛物线”为: 2y x ;(2)见解析;(3) 80 9a 或 8a .
【解析】
【分析】
(1)设 1L 的“友好抛物线”的表达式为: 2y x bx ,根据 2
1 : 2L y x x 可得其顶点坐标,
代入 2y x bx 可得b 的值,进而得出 1L 的“友好抛物线”;
(2)先求出抛物线 1L 和 2L 的顶点坐标,根据 2L 过 1L 的顶点,得出 0bn ,进而得到抛物线 1L 经
过 2L 的顶点,再根据 2L 与 1L 的开口大小相同,方向相反,即可得出抛物线 1L 也是 2L 的“友好
抛物线”;
(3)根据“友好抛物线”的定义,得到 m a ,进而得到 2L 的顶点为
2
,2 4
n n
a a
.
根据抛物线 2L 的顶点在第一象限,纵坐标为 2,可得 21 08a n .
再根据 2L 经过点 1,0P ,得到 8a .根据 2L 经过点 3,0Q ,得到 8
9a .
进而得出抛物线 2L 与线段 PQ 没有公共点时, a 的取值范围.
【详解】
解:(1)依题意,可设 1L 的“友好抛物线”的表达式为: 2y x bx ,
∵ 22
1 : 2 1 1L y x x x ,
∴ 1L 的顶点为 1, 1 .
∵ 2y x bx 过点 1, 1 ,
∴ 21 1 b ,即 0b .
∴ 1L 的“友好抛物线”为: 2y x .
(2) 2
2 :L y mx nx 的顶点为
2
,2 4
n n
m m
,
2
1 :L y ax bx 的顶点为
2
,2 4
b b
a a
,
∵ 2L 为 1L 的“友好抛物线”,
∴ m a .
∵ 2L 过 1L 的顶点,
∴
22
4 2 2
b b bm na a a
.
化简得: 0bn .
把 2
nx m
代入 2y ax bx ,得
2 2 2
2 2 4 2 4
n n n bn ny a bm m m m m
.
∴抛物线 1L 经过 2L 的顶点.
又∵ 2L 与 1L 的开口大小相同,方向相反,
∴抛物线 1L 也是 2L 的“友好抛物线”.
(3)∵抛物线 2
2 :L y mx nx 为 2
1 :L y ax 的“友好抛物线”,
∴ m a .
∴ 2
2 :L y ax nx 的顶点为
2
,2 4
n n
a a
.
∵抛物线 2L 的顶点在第一象限,纵坐标为 2,
∴
2
24
n
a
,即 21 08a n .
当 2L 经过点 1,0P 时, 0a n ,
∴ 8a .
当 2L 经过点 3,0Q 时, 9 3 0a n ,
∴ 8
9a .
由此可知: 8 89 a 时,抛物线 2L 与线段 PQ 有公共点,
∴抛物线 2L 与线段 PQ 没有公共点时, 80 9a 或 8a .
【点睛】
此题考查的是二次函数的综合大题,读懂“友好抛物线”的定义并根据“友好抛物线”的定义
解决实际问题、抛物线的顶点坐标公式和用方程思想解决问题是解决此题的关键.
24.定义:由两条与 x 轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为
“月牙线”.如图,抛物线 C1 与抛物线 C2 组成一个开口向上的“月牙线”,抛物线 C1 与抛
物线 C2 与 x 轴有相同的交点 M,N(点 M 在点 N 的左侧),与 y 轴的交点分别为 A,B 且点
A 的坐标为(0,﹣3),抛物线 C2 的解析式为 y=mx2+4mx﹣12m,(m>0).
(1)请你根据“月牙线”的定义,设计一个开口向下.“月牙线”,直接写出两条抛物线的
解析式;
(2)求 M,N 两点的坐标;
(3)在第三象限内的抛物线 C1 上是否存在一点 P,使得△PAM 的面积最大?若存在,求出
△PAM 的面积的最大值;若不存在,说明理由.
【答案】(1)抛物线 y=﹣x2+2x+3 与抛物线 y=﹣ 1
3 x2+ 2
3 x+1 所围成的封闭曲线即为开口向
下的“月牙线”;(2)M(﹣6,0),N(2,0);(3)存在,点 P 的坐标为(﹣3,﹣ 15
4 )时,
△PAM 的面积有最大值,最大值为 27
4 .
【解析】
【分析】
(1)根据定义,只要写出的两个抛物线与 x 轴有着相同的交点,且 a 的值为负即可;
(2)在解析式 y=mx2+4mx-12m 中,令 y=0 解方程即可求出 M,N 的横坐标,由此可写出
M,N 两点的坐标;
(3)先根据“月牙线”的定义,设出抛物线 C1 的一般式,将 A 点代入即可求得抛物线 C1
的解析式,再用含 t 的代数式表示 P 点坐标,根据 S△PAM=S△PMO+S△PAO-S△AOM 即可表示△PAM
的面积.可根据二次函数的性质求出面积的最大值以及此时 P 点坐标.
【详解】
(1)如图 1,
抛物线 y=﹣x2+2x+3 与抛物线 y=﹣ 1
3 x2+ 2
3 x+1 所围成的封闭曲线即为开口向下的“月牙
线”(此题答案不唯一);
(2)在抛物线 C2 的解析式 y=mx2+4mx﹣12m 中,
当 y=0 时,mx2+4mx﹣12m=0,
∵m≠0,
∴x2+4x﹣12=0,
解得,x1=﹣6,x2=2,
∵点 M 在点 N 的左边,
∴M(﹣6,0),N(2,0);
(3)存在,理由如下:
如图 2,连接 AM,PO,PM,PA,
∵抛物线 C1 和抛物线 C2 与 x 轴有着相同的交点,并且开口方向相同,
∴可设抛物线 C1 的解析式 y=nx2+4nx﹣12n(n>0),
∵抛物线 C1 与 y 轴的交点为 A(0,﹣3),
∴﹣12n=﹣3,
∴n= 1
4 ,
∴抛物线 C1 的解析式为 y= 1
4 x2+x﹣3,
∴可设点 P 的坐标为(t, 1
4 t2+t﹣3),
∴S△PAM=S△PMO+S△PAO﹣S△AOM
= 1
2 ×6×(﹣ 1
4 t2﹣t+3)+ 1
2 ×3×(﹣t)﹣ 1
2 ×6×3
=﹣ 3
4 t2﹣ 9
2 t,
=﹣ 3
4 (t+3)2+ 27
4 ,
∵﹣ 3
4 <0,﹣6<t<0,
∴根据二次函数的图象和性质知,当 t=﹣3 时,即点 P 的坐标为(﹣3,﹣ 15
4 )时,△PAM
的面积有最大值,最大值为 27
4 .
【点睛】
本题考查用待定系数法求二次函数解析式,二次函数与图形问题,二次函数图象及性质,二次
函数与坐标轴的交点.(1)中理解“月牙线”的定义是解题关键;(2)二次函数
2 ( 0)y ax bx c a ,当 0y 时,得到一元二次方程 2 0(a 0) ax bx c . 一元二次方程的解
就是二次函数的图象与 x 轴交点的横坐标;(3)能利用割补法表示△PAM 的面积是解题关键.
25.小贤与小杰在探究某类二次函数问题时,经历了如下过程:
求解体验
(1)已知抛物线 2 3y x bx 经过点(-1,0),则b = ,顶点坐标
为 ,该抛物线关于点(0,1)成中心对称的抛物线的表达式
是 .
抽象感悟
我们定义:对于抛物线 2 0y ax bx c a ,以 y 轴上的点 0,M m 为中心,作该抛物线
关于
点 M 对称的抛物线 'y ,则我们又称抛物线 'y 为抛物线 y 的“衍生抛物线”,点 M 为“衍生中
心”.
(2)已知抛物线 2 2 5y x x 关于点 0,m 的衍生抛物线为 'y ,若这两条抛物线有交点,
求 m 的取值范围.
问题解决
(3) 已知抛物线 2 2 0y ax ax b a
①若抛物线 y 的衍生抛物线为 2 22 0y bx bx a b ,两抛物线有两个交点,且恰好
是它们的顶点,求a b, 的值及衍生中心的坐标;
②若抛物线 y 关于点 20, 1k 的衍生抛物线为 1y ,其顶点为 1A ;关于点 20, 2k 的
衍生抛物线为 2y ,其顶点为 2A ;…;关于点 20,k n 的衍生抛物线为 ny ,其顶点为 nA ;…(n
为
正整数).求 1n nA A 的长(用含n 的式子表示).
【答案】求解体验: 4b ;顶点坐标是(-2,1); 2 4 5y x x ;抽象感悟: 5m ;问题解
决:①
3
3
a
b
;(0,6);② 4n 2
【解析】
【分析】(1)把(-1,0)代入 2 3y x bx 即可未出b =-4,然后把抛物线解析式变为顶点式即
可求得抛物线的顶点坐标,继而可得顶点关于(0,1)的对称点,从而可写出原抛物线关于点
(0,1)成中心对称的抛物线的表达式;
(2)先求出抛物线 2 2 5y x x 的顶点是(-1,6),从而求出 (-1,6)关于 0 m, 的对称
点是 1 2 6m, ,得 2' 1 2 6y x m ,根据两抛物线有交点,可以确定方程
2 21 6 1 2 6x x m 有解,继而求得 m 的取值范围即可;
(3) ①先求出抛物线 2 2 0y ax ax b a 以及抛物线 y 的衍生抛物线为
2 22 0y bx bx a b ,的顶点坐标,根据两抛物线有两个交点,且恰好是它们的顶点,求
a b, 的值及再根据中点坐标公式即可求出衍生中心的坐标;
② 如图,设 1AA , 2AA … nAA , n 1AA 与 y 轴分别相于 1B , 2B … nB , n 1B ,
则 1A A与 , 2A A与 ,… nA A与 , n 1A A 与 分别关于 1B , 2B … nB , n 1B 中心对称,由
题意则可得 1 2B B , 2 3B B … n n 1B B 分别是△ 1 2AA A , 2 3AA A … n n 1AA A 的中位线,继
而可得 1 2 1 2A A 2B B , 2 3 2 3A A 2B B ,… n n 1 n n 1A A 2B B ,再根据点的坐标即可求得 n n 1A A
的长.
【详解】求解体验
(1)把(-1,0)代入 2 3y x bx 得 4b ,
∴ 22 4 3 2 1y x x x- ,
∴顶点坐标是(-2,1),
∵(-2,1)关于(0,1)的对称点是(2,1),
∴成中心对称的抛物线表达式是: 22 1y x ,
即 2 4 5y x x (如图)
抽象感悟
(2) ∵ 22 2 5 1 6y x x x ,
∴ 顶点是(-1,6),
∵ (-1,6)关于 0 m, 的对称点是 1 2 6m, ,
∴ 2' 1 2 6y x m ,
∵ 两抛物线有交点,
∴ 2 21 6 1 2 6x x m 有解,
∴ 2 5x m 有解,
∴ 5 0m ,
∴ 5m ;(如图)
问题解决
(3) ① ∵ 2 2y ax ax b = 21a x a b ,
∴ 顶点(-1, a b ),
代入 2 22y bx bx a 得: 22b b a a b ①
∵ 22 2 22 1y bx bx a b x a b ,
∴ 顶点(1, 2a b ),
代入 2 2y ax ax b 得: 22a a b a b ②
由① ② 得
2
2
4 0
3 0
a a b
a a
,
∵ 0a , 0b ,
∴
3
3
a
b
,
∴ 两顶点坐标分别是(-1,0),(1,12),
由中点坐标公式得“衍生中心”的坐标是(0,6);
② 如图,设 1AA , 2AA … nAA , n 1AA 与 y 轴分别相于 1B , 2B … nB , n 1B ,
则 1A A与 , 2A A与 ,… nA A与 , n 1A A 与 分别关于 1B , 2B … nB , n 1B 中心对称,
∴ 1 2B B , 2 3B B … n n 1B B 分别是△ 1 2AA A , 2 3AA A … n n 1AA A 的中位线,
∴ 1 2 1 2A A 2B B , 2 3 2 3A A 2B B ,… n n 1 n n 1A A 2B B ,
∵ 2
nB 0 k n, , 2
n 1B 0 1k n , ,
∴ n n 1 n n 1A A 2B B 2 22 1 (k n k n ] 4n 2 .
【点睛】本题考查了二次函数的综合题,理解题意,画出符合题意的图形借助数形结合思想解
决问题是关键.