2010中考数学试题分类综合型问题
一、选择题
1.(2010江苏苏州)如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是
A.2 B.1 C. D.
【答案】C
2.(2010湖北十堰)如图,点C、D是以线段AB为公共弦的两条圆弧的中点,AB=4,点E、F分别是线段CD,AB上的动点,设AF=x,AE2-FE2=y,则能表示y与x的函数关系的图象是( )
(第10题分析图)
C
D
E
F
A
B
P
(第10题)
C
D
E
F
A
B
O
x
y
4
4
A.
O
x
y
4
4
B.
O
x
y
4
4
C.
O
x
y
4
4
D.
【答案】C
3.(2010 重庆江津)如图,等腰Rt△ABC(∠ACB=90º)的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让△ABC沿这条直线向右平移,直到点A与点E重合为止.设CD的长为,△ABC与正方形DEFG重合部分(图中阴影部分)的面积为,则与之间的函数关系的图象大致是( )
【答案】A
二、填空题
1.(2010浙江宁波) 如图,已知⊙P的半径为2,圆心P在抛物线上运动,当⊙P与轴相切时,圆心P的坐标为 ▲ .
【答案】或(对一个得2分)
三、解答题
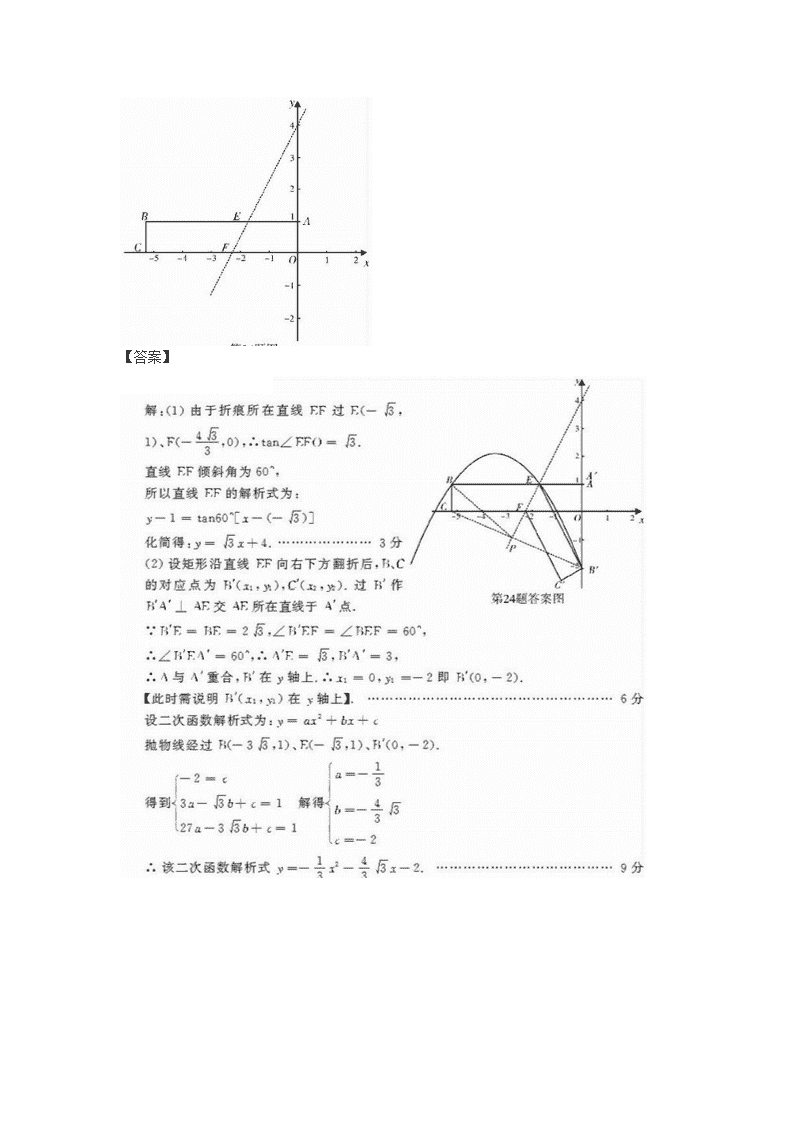
1.(2010安徽芜湖)(本小题满分14分)如图,在平面直角坐标系中放置一矩形ABCO,其顶点为A(0,1)、B(-3,1)、C(-3,0)、O(0,0).将此矩形沿着过E(-,1)、F(-,0)的直线EF向右下方翻折,B、C的对应点分别为B′、C′.
(1)求折痕所在直线EF的解析式;
(2)一抛物线经过B、E、B′三点,求此二次函数解析式;
(3)能否在直线EF上求一点P,使得△PBC周长最小?如能,求出点P的坐标;若不能,说明理由.
【答案】
2.(2010广东广州,24,14分)如图,⊙O的半径为1,点P是⊙O上一点,弦AB垂直平分线段OP,点D是上任一点(与端点A、B不重合),DE⊥AB于点E,以点D为圆心、DE长为半径作⊙D,分别过点A、B作⊙D的切线,两条切线相交于点C.
(1)求弦AB的长;
(2)判断∠ACB是否为定值,若是,求出∠ACB的大小;否则,请说明理由;
(3)记△ABC的面积为S,若=4,求△ABC的周长.
C
P
D
O
B
A
E
【答案】解:(1)连接OA,取OP与AB的交点为F,则有OA=1.
F
C
P
D
O
B
A
E
H
G
∵弦AB垂直平分线段OP,∴OF=OP=,AF=BF.
在Rt△OAF中,∵AF===,∴AB=2AF=.
(2)∠ACB是定值.
理由:由(1)易知,∠AOB=120°,
因为点D为△ABC的内心,所以,连结AD、BD,则∠CAB=2∠DAE,∠CBA=2∠DBA,
因为∠DAE+∠DBA=∠AOB=60°,所以∠CAB+∠CBA=120°,所以∠ACB=60°;
(3)记△ABC的周长为l,取AC,BC与⊙D的切点分别为G,H,连接DG,DC,DH,则有DG=DH=DE,DG⊥AC,DH⊥BC.
∴
=AB•DE+BC•DH+AC•DG=(AB+BC+AC) •DE=l•DE.
∵=4,∴=4,∴l=8DE.
∵CG,CH是⊙D的切线,∴∠GCD=∠ACB=30°,
∴在Rt△CGD中,CG===DE,∴CH=CG=DE.
又由切线长定理可知AG=AE,BH=BE,
∴l=AB+BC+AC=2+2DE=8DE,解得DE=,
∴△ABC的周长为.
3.(2010江苏南京)(8分)如图,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止,连接EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,连结EG、FG。
(1)设AE=时,△EGF的面积为,求关于的函数关系式,并写出自变量的取值范围;
(2)P是MG的中点,请直接写出点P的运动路线的长。
【答案】
4.(2010江苏南通)(本小题满分12分)
如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若,要使△DEF为等腰三角形,m的值应为多少?
A
B
C
D
E
F
(第27题)
【答案】⑴在矩形ABCD中,∠B=∠C=Rt∠,
∴在Rt△BFE中, ∠1+∠BFE=90°,
又∵EF⊥DE ∴∠1+∠2=90°,∴∠2=∠BFE,∴Rt△BFE∽Rt△CED
∴即∴
⑵当=8时, ,化成顶点式: ,
∴当=4时,的值最大,最大值是2.
⑶由,及得的方程: ,得, ,
∵△DEF中∠FED是直角,
∴要使△DEF是等腰三角形,则只能是EF=ED,
此时, Rt△BFE≌Rt△CED,
∴当EC=2时,=CD=BE=6;
当EC=6时,=CD=BE=2.
即的值应为6或2时, △DEF是等腰三角形.
5.(2010江苏南通)(本小题满分14分)
已知抛物线y=ax2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与 x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax2+bx+c上的动点,当
△PDO的周长最小时,求四边形CODP的面积.
-1
y
x
O
(第28题)
1
2
3
4
-2
-4
-3
3
-1
-2
-3
-4
4
1
2
【答案】(1)因为当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,故b=0.
设直线AB的解析式为y=kx+b,把A(-4,3)、B(2,0)代入到y=ax2+bx+c,得
解得
∴这条抛物线的解析式为y=x2-1.
设直线AB的解析式为y=kx+b,把A(-4,3)、B(2,0)代入到y=kx+b,得
解得
∴这条直线的解析式为y=-x+1.
(2)依题意,OA=即⊙A的半径为5.
而圆心到直线l的距离为3+2=5.
即圆心到直线l的距离=⊙A的半径,
∴直线l与⊙A相切.
(3)由题意,把x=-1代入y=-x+1,得y=,即D(-1,).
由(2)中点A到原点距离跟到直线y=-2的距离相等,且当点A成为抛物线上一个动点时,仍然具有这样的性质,于是过点D作DH⊥直线l于H,交抛物线于点P,此时易得DH是D点到l最短距离,点P坐标(-1,-)此时四边形PDOC为梯形,面积为.
6.(2010江苏盐城)(本题满分12分)如图1所示,在直角梯形ABCD中,AD∥BC,AB⊥BC,∠DCB=75º,以CD为一边的等边△DCE的另一顶点E在腰AB上.
(1)求∠AED的度数;
(2)求证:AB=BC;
(3)如图2所示,若F为线段CD上一点,∠FBC=30º.
求 的值.
【答案】
7.(2010山东烟台)(本题满分14分)
如图,已知抛物线y=x2+bx-3a过点A(1,0),B(0,-3),与x轴交于另一点C。
(1)求抛物线的解析式;
(2)若在第三象限的抛物线上存在点P,使△PBC为以点B为直角顶点的直角三角形,求点P的坐标;
(3)在(2)的条件下,在抛物线上是否存在一点Q,使以P,Q,B,C为顶点的四边形为直角梯形?若存在,请求出点Q的坐标;若不存在,请说明理由。
【答案】
8.(2010四川凉山)已知:抛物线,顶点,与轴交于A、
B两点,。
(1) 求这条抛物线的解析式;
(2) 如图,以AB为直径作圆,与抛物线交于点D,与抛物线的对称轴交于点F,依次连接A、D、B、E,点Q为线段AB上一个动点(Q与A、B两点不重合),过点Q作于,于,请判断是否为定值;若是,请求出此定值,若不是,请说明理由;
(3) 在(2)的条件下,若点H是线段EQ上一点,过点H作,分别与边、相交于、,(与、不重合,与、不重合),请判断是否成立;若成立,请给出证明,若不成立,请说明理由。
第26题图
A
B
x
G
F
M
H
E
N
Q
O
D
C
y
【答案】
9.(2010四川眉山)如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(,0)、(0,4),抛物线经过B点,且顶点在直线上.
(1)求抛物线对应的函数关系式;
(2)若△DCE是由△ABO沿x轴向右平移得到的,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)若M点是CD所在直线下方该抛物线上的一个动点,过点M作MN平行于y轴交CD于点N.设点M的横坐标为t,MN的长度为l.求l与t之间的函数关系式,并求l取最大值时,点M的坐标.
【答案】
解:(1)由题意,可设所求抛物线对应的函数关系式为 …(1分)
∴
∴ ……………………………………………………………(3分)
∴所求函数关系式为: …………(4分)
(2)在Rt△ABO中,OA=3,OB=4,
∴
∵四边形ABCD是菱形
∴BC=CD=DA=AB=5 ……………………………………(5分)
∴C、D两点的坐标分别是(5,4)、(2,0). …………(6分)
当时,
当时,
∴点C和点D在所求抛物线上. …………………………(7分)
(3)设直线CD对应的函数关系式为,则
解得:.
∴ ………(9分)
∵MN∥y轴,M点的横坐标为t,
∴N点的横坐标也为t.
则, ,……………………(10分)
∴
∵, ∴当时,,
此时点M的坐标为(,). ………………………………(12分)
10.(2010浙江杭州) (本小题满分12分)
(第24题)
在平面直角坐标系xOy中,抛物线的解析式是y =+1,
点C的坐标为(–4,0),平行四边形OABC的顶点A,B在抛物
线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点
P(t,0)在x轴上.
(1) 写出点M的坐标;
(2) 当四边形CMQP是以MQ,PC为腰的梯形时.
① 求t关于x的函数解析式和自变量x的取值范围;
② 当梯形CMQP的两底的长度之比为1:2时,求t的值.
【答案】
(本小题满分12分)
(第24题)
(1) ∵OABC是平行四边形,∴AB∥OC,且AB = OC = 4,
∵A,B在抛物线上,y轴是抛物线的对称轴,
∴ A,B的横坐标分别是2和– 2,
代入y =+1得, A(2, 2 ),B(– 2,2),
∴M (0,2), ---2分
(2) ① 过点Q作QH ^ x轴,设垂足为H, 则HQ = y ,HP = x–t ,
由△HQP∽△OMC,得:, 即: t = x – 2y ,
∵ Q(x,y) 在y = +1上, ∴ t = –+ x –2. ---2分
当点P与点C重合时,梯形不存在,此时,t = – 4,解得x = 1±,
当Q与B或A重合时,四边形为平行四边形,此时,x = ± 2
∴x的取值范围是x ¹ 1±, 且x¹± 2的所有实数. ---2分
② 分两种情况讨论:
1)当CM > PQ时,则点P在线段OC上,
∵ CM∥PQ,CM = 2PQ ,
∴点M纵坐标为点Q纵坐标的2倍,即2 = 2(+1),解得x = 0 ,
∴t = –+ 0 –2 = –2 . --- 2分
2)当CM < PQ时,则点P在OC的延长线上,
∵CM∥PQ,CM = PQ,
∴点Q纵坐标为点M纵坐标的2倍,即+1=2´2,解得: x = ±. ---2分
当x = –时,得t = –––2 = –8 –,
当x=时, 得t =–8. ---2分
11.(2010浙江宁波)如图1,在平面直角坐标系中,O是坐标原点,□ABCD的顶点A的坐标为(-2,0),点
D的坐标为 (0,),点B在轴的正半轴上,点E为线段AD的中点,过点E的直
线与轴交于点F,与射线DC交于点G.
(1)求∠DCB的度数;
(2)当点F的坐标为(-4,0)时,求点G的坐标;
(3)连结OE,以OE所在直线为对称轴,△OEF经轴对称变换后得到△OEF’,记直线EF’与射线DC的交点为H.
①如图2,当点G在点H的左侧时,求证:△DEG∽△DHE;
②若△EHG的面积为,请直接写出点F的坐标.
(图2)
(图1)
【答案】
解:(1) 在Rt△AOD中,
∵tan∠DAO=,
∴ ∠DAB=60°. 2分
∵四边形ABCD是平行四边形
∴∠DCB=∠DAB=60° 3分
(2) ∵四边形ABCD是平行四边形
∴CD∥AB
∴∠DGE=∠AFE
又∵∠DEG=∠AEF,DE=AE
∴△DEG≌△AEF 4分
∴DG=AF
∵AF=OF-OA=4-2=2
∴DG=2
∴点G的坐标为(2,) 6分
(3)①∵CD∥AB
∴∠DGE=∠OFE
∵△OEF经轴对称变换后得到△OEF’
∴∠OFE=∠OF’E 7分
∴∠DGE=∠OF’E
在Rt△AOD中,∵E是AD的中点 ∴OE=AD=AE
又∵∠EAO=60°
∴∠EOA=60°, ∠AEO=60°
又∵∠EOF’=∠EOA=60°
∴∠EOF’=∠OEA
∴AD∥OF’ 8分
∴∠OF′E=∠DEH
∴∠DEH=∠DGE
又∵∠HDE=∠EDG
∴△DHE∽△DEG 9分
②点F的坐标是F1(,0),F2(,0). 12分
(给出一个得2分)
对于此小题,我们提供如下详细解答,对学生无此要求.
过点E作EM⊥直线CD于点M,
M
∵CD∥AB
∴∠EDM=∠DAB=60°
∴
∵
∴
∵△DHE∽△DEG
∴ 即
当点在点的右侧时,设,
∴
解得:(舍)
∵△DEG≌△AEF
∴AF=DG=
∵OF=AO+AF=
∴点F的坐标为(,0)
当点在点的左侧时,设,
∴
解得:(舍)
∵△DEG≌△AEF
∴AF=DG=
∵OF=AO+AF=
∴点F的坐标为(,0)
综上可知, 点F的坐标有两个,分别是F1(,0),F2(,0).
12.(2010浙江绍兴)如图,设抛物线C1:, C2:,C1与C2的交点为A, B,点A的坐标是,点B的横坐标是-2.
第24题图
(1)求的值及点B的坐标;
(2)点D在线段AB上,过D作x轴的垂线,垂足为点H,
在DH的右侧作正三角形DHG. 记过C2顶点M的
直线为,且与x轴交于点N.
① 若过△DHG的顶点G,点D的坐标为
(1, 2),求点N的横坐标;
② 若与△DHG的边DG相交,求点N的横
坐标的取值范围.
【答案】
解:(1)∵ 点A在抛物线C1上,∴ 把点A坐标代入得 =1.
∴ 抛物线C1的解析式为,
设B(-2,b), ∴ b=-4, ∴ B(-2,-4) .
(2)①如图1,
∵ M(1, 5),D(1, 2), 且DH⊥x轴,∴ 点M在DH上,MH=5.
过点G作GE⊥DH,垂足为E,
第24题图1
由△DHG是正三角形,可得EG=, EH=1,
∴ ME=4.
设N ( x, 0 ), 则 NH=x-1,
由△MEG∽△MHN,得 ,
∴ , ∴ ,
∴ 点N的横坐标为.
第24题图2
② 当点D移到与点A重合时,如图2,
直线与DG交于点G,此时点N的横坐标最大.
过点G,M作x轴的垂线,垂足分别为点Q,F,
设N(x,0),
∵ A (2, 4), ∴ G (, 2),
∴ NQ=,NF =, GQ=2, MF =5.
∵ △NGQ∽△NMF,
∴ ,
第24题图3
图4
∴ ,
∴ .
当点D移到与点B重合时,如图3,
直线与DG交于点D,即点B,
此时点N的横坐标最小.
∵ B(-2, -4), ∴ H(-2, 0), D(-2, -4),
设N(x,0),
∵ △BHN∽△MFN, ∴ ,
∴ , ∴ .
∴ 点N横坐标的范围为 ≤x≤.
13.(2010山东聊城)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(-1,0)、C(0,-3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A
的距离与到点C的距离之和最小,并求此时点M的坐标;
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90º的点P的坐标.
E
【答案】解:(1)∵抛物线经过点C(0,-3)∴C=-3,∴y=ax2+bx-3,又抛物线经过点A(-1,0),对称轴为x=1,所以
∴抛物线的函数关系式为y=x2-2x-3
(2)∵点A(-1,0),对称轴为x=1,∴点B(2,0).
设直线BC的函数关系式为y=kx+b,根据题意得
∴直线BC的函数关系式为y=-3x-3,当x=1时,y=-6,∴点P的坐标为(1,-6).
(3)如图,过点P作PD⊥OC,设P(1,y),则PE=|y|,DC=|-3-y|,
在Rt△PEB中,PB2=22+|y|2=4+y2,在Rt△PCD中PC2=12+|-3-y|2=10+6y+y2,在Rt△OBC中,BC2=32+32=18,∵∠PCD=90º,∴PB2+PC2=BC2,∴4+y2+10+6y+y2=18,整理得y2+3y-2=0解得y1=,y2=.
14.(2010 福建晋江)(13分)已知:如图,把矩形放置于直角坐标系中,,,取的中点,连结,把沿轴的负方向平移的长度后得到.
(1)试直接写出点的坐标;
(2)已知点与点在经过原点的抛物线上,点在第一象限内的该抛物线上移动,过点作轴于点,连结.
①若以、、为顶点的三角形与相似,试求出点的坐标;
②试问在抛物线的对称轴上是否存在一点,使得的值最大.
A
O
x
B
C
M
y
【答案】
A
O
x
D
B
C
M
y
E
P
T
Q
解:(1)依题意得:;…………………………………………………(3分)
(2) ① ∵,,∴.
∵抛物线经过原点,
∴设抛物线的解析式为
又抛物线经过点与点
∴ 解得:
∴抛物线的解析式为.…………………(5分)
∵点在抛物线上,
∴设点.
1)若∽,则, ,解得:(舍去)或
,
∴点.………………………………………………………………(7分)
2)若∽,则, ,解得:(舍去)或,
∴点.……………………………………………………………………(9分)
②存在点,使得的值最大.
抛物线的对称轴为直线,设抛物线与轴的另一个交点为,则点.………………………………………………………………………(10分)
∵点、点关于直线对称,
∴……………………………………………………………………(11分)
要使得的值最大,即是使得的值最大,
根据三角形两边之差小于第三边可知,当、、三点在同一直线上时,的值最大. ……………………………………………………………………………(12分)
设过、两点的直线解析式为,
∴ 解得:
∴直线的解析式为.
当时,.
∴存在一点使得最大.………………………(13分)
15.(2010 四川南充)已知抛物线上有不同的两点E和F.
(1)求抛物线的解析式.
(2)如图,抛物线与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式.
(3)当m,n为何值时,∠PMQ的边过点F.
B
A
M
C
D
O
P
Q
x
y
【答案】
11. 解:(1)抛物线的对称轴为. ……..(1分)
∵ 抛物线上不同两个点E和F的纵坐标相同,
∴ 点E和点F关于抛物线对称轴对称,则 ,且k≠-2.
∴ 抛物线的解析式为. ……..(2分)
(2)抛物线与x轴的交点为A(4,0),与y轴的交点为B(0,4),
∴ AB=,AM=BM=. ……..(3分)
在∠PMQ绕点M在AB同侧旋转过程中,∠MBC=∠DAM=∠PMQ=45°,
在△BCM中,∠BMC+∠BCM+∠MBC=180°,即∠BMC+∠BCM=135°,
在直线AB上,∠BMC+∠PMQ+∠AMD=180°,即∠BMC+∠AMD=135°.
∴ ∠BCM=∠AMD.
故 △BCM∽△AMD. ……..(4分)
∴ ,即 ,.
故n和m
之间的函数关系式为(m>0). ……..(5分)
(3)∵ F在上,
∴ ,
化简得,,∴ k1=1,k2=3.
即F1(-2,0)或F2(-4,-8). ……..(6分)
①MF过M(2,2)和F1(-2,0),设MF为,
则 解得, ∴ 直线MF的解析式为.
直线MF与x轴交点为(-2,0),与y轴交点为(0,1).
若MP过点F(-2,0),则n=4-1=3,m=;
若MQ过点F(-2,0),则m=4-(-2)=6,n=. ……..(7分)
②MF过M(2,2)和F1(-4,-8),设MF为,
则 解得, ∴ 直线MF的解析式为.
直线MF与x轴交点为(,0),与y轴交点为(0,).
若MP过点F(-4,-8),则n=4-()=,m=;
若MQ过点F(-4,-8),则m=4-=,n=. ……..(8分)
故当 或时,∠PMQ的边过点F.
16.(2010 四川南充)如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC, OE=BC.
(1)求∠BAC的度数.
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H.求证:四边形AFHG是正方形.
(3)若BD=6,CD=4,求AD的长.
A
F
C
D
E
G
H
B
O
A
F
C
D
E
G
H
B
O
【答案】(1)解:连结OB和OC.
A
F
C
D
E
G
H
B
O
∵ OE⊥BC,∴ BE=CE.
∵ OE=BC,∴ ∠BOC=90°,∴ ∠BAC=45°.
(2)证明:∵ AD⊥BC,∴ ∠ADB=∠ADC=90°.
由折叠可知,AG=AF=AD,∠AGH=∠AFH=90°,
∠BAG=∠BAD,∠CAF=∠CAD,
∴ ∠BAG+∠CAF=∠BAD+∠CAD=∠BAC=45°.
∴ ∠GAF=∠BAG+∠CAF+∠BAC=90°.
∴ 四边形AFHG是正方形.
(3)解:由(2)得,∠BHC=90°,GH=HF=AD,GB=BD=6,CF=CD=4.
设AD的长为x,则 BH=GH-GB=x-6,CH=HF-CF=x-4.
在Rt△BCH中,BH2+CH2=BC2,∴ (x-6)2+(x-4)2=102.
解得,x1=12,x2=-2(不合题意,舍去).
∴ AD=12.
17.(2010 山东济南)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.
(1)求k的值;
(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;
(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.
【答案】(1)∵点A横坐标为4 ,
∴当 x = 4时,y = 2
∴ 点A的坐标为(4,2 ) …………2’
∵点A是直线与双曲线(k>0)的交点,
∴ k = 4×2 = 8 ………….3’
(2)解法一:
∵ 点C在双曲线上,当y = 8时,x = 1
∴ 点C的坐标为(1,8)………..4’
过点A、C分别做x轴、y轴的垂线,垂足为M、N,得矩形DMON
S矩形ONDM= 32 , S△ONC = 4 , S△CDA = 9, S△OAM = 4
S△AOC= S矩形ONDM-S△ONC-S△CDA-S△OAM
= 32-4-9-4 = 15 ………..6’
解法二:
过点 C、A分别做轴的垂线,垂足为E、F,
∵ 点C在双曲线上,当y = 8时,x = 1。
∴ 点C的坐标为(1,8)
∵ 点C、A都在双曲线上,
∴ S△COE = S△AOF = 4
∴ S△COE + S梯形CEFA = S△COA + S△AOF .
∴ S△COA = S梯形CEFA
∵ S梯形CEFA =×(2+8)×3 = 15,
∴ S△COA = 15
(3)∵ 反比例函数图象是关于原点O的中心对称图形 ,
∴ OP=OQ,OA=OB
∴ 四边形APBQ是平行四边形
∴ S△POA = S平行四边形APBQ =×24 = 6
设点P的横坐标为m(m > 0且),
得P(m,) …………..7’
过点P、A分别做轴的垂线,垂足为E、F,
∵ 点P、A在双曲线上,∴S△POE = S△AOF = 4
若0<m<4,
∵ S△POE + S梯形PEFA = S△POA + S△AOF,
∴ S梯形PEFA = S△POA = 6
∴
解得m= 2,m= - 8(舍去)
∴ P(2,4) ……………8’
若 m> 4,
∵ S△AOF+ S梯形AFEP = S△AOP + S△POE,
∴ S梯形PEFA = S△POA = 6
∴,
解得m= 8,m =-2 (舍去)
∴ P(8,1)
∴ 点P的坐标是P(2,4)或P(8,1)………….9’
18.(2010江苏泰州)在平面直角坐标系中,直线(k为常数且k≠0)分别交x轴、y轴于点A、B,⊙O半径为个单位长度.
⑴如图甲,若点A在x轴正半轴上,点B在y轴正半轴上,且OA=OB.
①求k的值;
②若b=4,点P为直线上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,当PC⊥PD时,求点P的坐标.
⑵若,直线将圆周分成两段弧长之比为1∶2,求b的值.(图乙供选用)
【答案】⑴①根据题意得:B的坐标为(0,b),∴OA=OB=b,∴A的坐标为(b,0),代入y=kx+b得k=-1.
②过P作x轴的垂线,垂足为F,连结OD.
∵PC、PD是⊙O的两条切线,∠CPD=90°,
∴∠OPD=∠OPC=∠CPD=45°,
∵∠PDO=90°,,∠POD=∠OPD=45°,
∴OD=PD=,OP=.
∵P在直线y=-x+4上,设P(m,-m+4),则OF=m,PF=-m+4,
∵∠PFO=90°, OF2+PF2=PO2,
∴ m2+ (-m+4)2=()2, 全品中考网
解得m=1或3,
∴P的坐标为(1,3)或(3,1)
⑵分两种情形,y=-x+,或y=-x-。
直线将圆周分成两段弧长之比为1∶2,可知其所对圆心角为120°,如图,画出弦心距OC,可得弦心距OC=,又∵直线中∴直线与x轴交角的正切值为,即,∴AC=,进而可得AO=,即直线与与x轴交于点(,0).所以直线与y轴交于点(,0),所以b的值为.
当直线与x轴、y轴的负半轴相交,同理可求得b的值为.
综合以上得:b的值为或.
19.(2010湖南邵阳)如图(十四),抛物线y=与x轴交于点A、B,与y轴相交于点C,顶点为点D,对称轴l与直线BC相交于点E,与x轴交于点F。
(1)求直线BC的解析式;
(2)设点P为该抛物线上的一个动点,以点P为圆心,r为半径作⊙P。
①当点P运动到点D时,若⊙P与直线BC相交 ,求r的取值范围;
②若r=,是否存在点P使⊙P与直线BC相切,若存在,请求出点P的坐标;若不存在,请说明理由.
提示:抛物线y=的顶点坐标,对称轴x=.
图(十四)
【答案】解(1)令y=0,求得A点坐标为(-2,0),B点坐标为(6,0);
令x=0,求得C点的坐标为(0,3)
设BC直线为y=kx+b,把B、C点的坐标代入得: 解得k=,b=3
故BC的解析式为:y=x+3
(2)①过点D(2,4)作DG⊥BC于点G,因为抛物线的对称轴是直线x=2,所以点E的坐标为(2,2),所以有EF=2,FB=4,EB=2,DE=2,从图中可知,,所以有: 解得DG= 故当r>,点P
运动到点D时,⊙P与直线BC相交
②由①知,直线BC上方的点D符合要求。设过点D并与直线BC平行的直线为y=x+n,把点D的坐标代入,求得n=5,所以联立: 解得两点(2,4)为D点,(4,3)也符合条件。
设在直线BC下方到直线BC的距离为的直线m与x轴交于点M,过点M作MN⊥BC于点N,所以MN=,又tan∠NBM= 所以NB=,BM=4,所以点M与点F重合。设直线m为y=x+b 把点F的坐标,代入得:0=×2+b 得b=1,所以直线m的解析式为:y=x+1
联立方程组: 解得:x=
所以适合要求的点还有两点即(3-,)与(3+,)
故当r=,存在点P使⊙P与直线BC相切,符合条件的点P有四个,即是D
(2,4),(4,3)和(3-,),(3+,)的坐标.
20.(2010年上海)如图8,已知平面直角坐标系xOy,抛物线y=-x2+bx+c过点A(4,0)、B(1,3) .
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
图8
【答案】解:(1) 抛物线y=-x2+bx+c过点 A(4,0)B(1,3).∴
∴,,对称轴为直线,顶点坐标为
(2)∵直线EP∥OA,E与P两点关于直线对称,∴OE=AP,∴梯形OEPA为等腰梯形,
∴∠OEP=∠APE,∵OE=OF, ∴∠OEP=∠AFE,∴∠OFP=∠APE,∴OF∥AP,
∴四边形OAPF为平行四边形,∵四边形OAPF的面积为20,∴,
∴,∴.
21.(2010年上海)如图9,在Rt△ABC中,∠ACB=90°.半径为1的圆A与边AB相交于点D,与边AC相交于点E,连结DE并延长,与线段BC的延长线交于点P.
(1)当∠B=30°时,连结AP,若△AEP与△BDP相似,求CE的长;
(2)若CE=2,BD=BC,求∠BPD的正切值;
(3)若,设CE=x,△ABC的周长为y,求y关于x的函数关系式.
图9 图10(备用) 图11(备用)
【答案】解:(1)如图1,∵∠ACB=90°, ∠B=30°,∴∠BAC=60°,∵AD=AE=1∴ΔADE为等边三角形,∴∠ADE=∠AED=60°,∴∠BDE=∠AEP=120°,∠CEP=60°,∴∠EPC=30°=∠B,
∴ΔBDP为等腰三角形,∵ΔAPE与ΔBPD相似,∴ΔAPE为等腰三角形,AE=EP=1,
∴CE=EP=.
(2)设BC=BD=,∠ACB=90°,∴,∴=4 ,BC=BD=4,
过D作DH⊥BC交BC于H,如图2,∴DH∥AC,∴,∴,∴,
同理可得,∵DH∥AC,∴,,∴CP=4, ∵∠ECP=90°,∴=.
(3)如图3,当时,设CE=,∴CP=3,由(2),
∴设BD=,∴,,,,
∴,∴,∴=m+1+x+1+3m-3x=3x+3.
22.(2010 江苏连云港)(本题满分14分)如图,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为.函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为AB上一动点
(1)连接CO,求证:CO⊥AB;
(2)若△POA是等腰三角形,求点P的坐标;
(3)当直线PO与⊙C相切时,求∠POA的度数;当直线PO与⊙C相交时,设交点为E、F,点M为线段EF的中点,令PO=t,MO=s,求s与t
之间的函数关系,并写出t的取值范围.
AD
BAD
x
P
O
·
·
CFEBAD
y
【答案】
23.(2010 山东莱芜)如图,在平面直角坐标系中,已知抛物线交轴于两点,交轴于点.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线交于点D,作⊙D与x轴相切,⊙D交轴于点E、F两点,求劣弧EF的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
(第24题图)
x
y
O
A
C
B
D
E
F
【答案】解:(1)∵抛物线经过点,,.
∴, 解得.
∴抛物线的解析式为:.
(2)易知抛物线的对称轴是.把x=4代入y=2x得y=8,∴点D的坐标为(4,8).∵⊙D与x轴相切,∴⊙D的半径为8.
连结DE、DF,作DM⊥y轴,垂足为点M.
在Rt△MFD中,FD=8,MD=4.∴cos∠MDF=.
∴∠MDF=60°,∴∠EDF=120°.
∴劣弧EF的长为:.
x
y
O
A
C
B
D
E
F
P
G
N
M
(3)设直线AC的解析式为y=kx+b. ∵直线AC经过点.
∴,解得.∴直线AC的解析式为:.
设点,PG交直线AC于N,
则点N坐标为.∵.
∴①若PN︰GN=1︰2,则PG︰GN=3︰2,PG=GN.
即=.
解得:m1=-3, m2=2(舍去).当m=-3时,=.
∴此时点P的坐标为. ……………………………10分
②若PN︰GN=2︰1,则PG︰GN=3︰1, PG=3GN.
即=.
解得:,(舍去).当时,=.
∴此时点P的坐标为.
综上所述,当点P坐标为或时,
△PGA的面积被直线AC分成1︰2两部分.
24.(2010 广东珠海)如图,平面直角坐标系中有一矩形ABCD(O为原点),点A、C分别在x轴、y轴上,且C点坐标为(0,6);将BCD沿BD折叠(D点在OC边上),使C点落在OA边的E点上,并将BAE沿BE折叠,恰好使点A落在BD的点F上.
(1)直接写出∠ABE、∠CBD的度数,并求折痕BD所在直线的函数解析式;
(2)过F点作FG⊥x轴,垂足为G,FG的中点为H,若抛物线经过B、H、D三点,求抛物线的函数解析式;
(3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PM
MN成立的x的取值范围。
【答案】解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(,6) D(0,2)
设BD所在直线的函数解析式是y=kx+b
∴
所以BD所在直线的函数解析式是
(2)∵EF=EA=ABtan30°= ∠FEG=180°-∠FEB-∠AEB=60°
又∵FG⊥OA
∴FG=EFsin60°=3 GE=EFcos60°= OG=OA-AE-GE=
又H为FG中点
∴H(,) …………4分
∵B(,6) 、 D(0,2)、 H(,)在抛物线图象上
∴
∴抛物线的解析式是
(2)∵MP=
MN=6-
H=MP-MN=
由得
该函数简图如图所示:
当00,即HP>MN
25.(2010浙江湖州)如图,已知在直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D,将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴于E和F.
(1)求经过A,B,C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时
S最小,并求出这个最小值.
.
【答案】由题意得:A(0,2)、B(2,2)、C(3,0),设经过A,B,C三点的抛物线的解析式为,则,解得:,所以.
(2)由=,所以顶点坐标为G(1,),过G作GH⊥AB,垂足为H,则AH=BH=1,GH=-2=,∵EA⊥AB,GH⊥AB,∴EA∥GH,∴GH是△BEA的中位线,∴EA=3GH=,过B作BM⊥OC,垂足为M,则MB=OA=AB,∵∠EBF=∠ABM=90°,∴∠EBA=∠FBM=90°-∠ABF,∴R t△EBA≌R t△FBM,∴FM=EA=,∵CM=OC-OM=3-2=1,∴CF=FM+CM=.
(3)设CF=a,则FM= a-1或1- a,∴BF2=FM2+BM2=(a-1)2+22=a2-2a+5,又∵△EBA≌△FBM,∴BM=BF,
则,又,
∴S= ,即S=,∴当a=2(在2<a<3)时,.
26.(2010 湖南株洲)(本题满分10分)在平面直角坐标系中,抛物线过原点O,且与轴交于另一点,其顶点为.孔明同学用一把宽为带刻度的矩形直尺对抛物线进行如下测量:
① 量得;
②
把直尺的左边与抛物线的对称轴重合,使得直尺左下端点与抛物线的顶点重合(如图1),测得抛物线与直尺右边的交点的刻度读数为.
请完成下列问题:
(1)写出抛物线的对称轴;
(2)求抛物线的解析式;
(3)将图中的直尺(足够长)沿水平方向向右平移到点的右边(如图2),直尺的两边交轴于点、,交抛物线于点、.求证:.
图1
图2
·
B
【答案】(1)
(2)设抛物线的解析式为:,当时,,即;当时,,即,依题意得:,解得:.
∴抛物线的解析式为:.
(3)方法一:过点作,垂足为,设, ,得: ①
②
又,得,分别代入①、②得:,
∴
得:
又
∴
方法二:过点作,垂足为,设,则,得:
∵
∴
27.(2010 四川成都)已知:如图,内接于⊙O,为直径,弦于,是AD的中点,连结并延长交的延长线于点,连结,分别交、于点、.
(1)求证:是的外心;
(2)若,求的长;
(3)求证:.
【答案】(1)证明:∵C是AD的中点,∴AC=CD,
∴∠CAD=∠ABC⌒
∵AB是⊙O的直径,∴∠ACB=90°。
∴∠CAD+∠AQC=90°
又CE⊥AB,∴∠ABC+∠PCQ=90°
∴∠AQC=∠PCQ
⌒
⌒
∴在△PCQ中,PC=PQ,
⌒
⌒
∵CE⊥直径AB,∴AC=AE
∴AE=CD
∴∠CAD=∠ACE。
∴在△APC中,有PA=PC,
∴PA=PC=PQ
∴P是△ACQ的外心。
(2)解:∵CE⊥直径AB于F,
∴在Rt△BCF中,由tan∠ABC=,CF=8,
得。
∴由勾股定理,得
∵AB是⊙O的直径,
∴在Rt△ACB中,由tan∠ABC=,
得。
易知Rt△ACB∽Rt△QCA,∴
∴。
(3)证明:∵AB是⊙O的直径,∴∠ACB=90°
∴∠DAB+∠ABD=90°
又CF⊥AB,∴∠ABG+∠G=90°
∴∠DAB=∠G;
∴Rt△AFP∽Rt△GFB,
∴,即
易知Rt△ACF∽Rt△CBF,
∴
∴
由(1),知PC=PQ,∴FP+PQ=FP+PC=FC
∴。
28.(2010山东潍坊)如图所示,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于C(0,-3).以AB为直径做⊙M,过抛物线上的一点P作⊙M的切线PD,切点为D,并与⊙M的切线AE相交于点E.连接DM并延长交⊙M于点N,连接AN.
(1)求抛物线所对应的函数的解析式及抛物线的顶点坐标;
(2)若四边形EAMD的面积为4,求直线PD的函数关系式;
(3)抛物线上是否存在点P,使得四边形EAMD的面积等于△DAN的面积?若存在,求出点P的坐标,若不存在,说明理由.
【答案】解:(1)因为抛物线与x轴交于点A(-1,0)、B(3,0)两点,设抛物线的函数关系式为y=a(x+1)(x-3),∵抛物线与y轴交于C(0,-3),∴-3= a(0+1)(0-3),解得a=1,所以抛物线的解析式为y=x2-2x-3=(x-1)2-4,因此抛物线的顶点坐标为(1,-4);
(2)连接EM,∵EA、ED是⊙M的切线,∴EA=ED,EA⊥AM,ED⊥MD,∴△EAM≌△EDM,又四边形EAMD的面积为4,∴S△EAM=2,∴AM·AE=2,又AM=2,∴AE=2,因此E1(-1,2)或者E2(-1,-2),当点E在第二象限时,切点D在第一象限,在 Rt△EAM中,tan∠EMA=,故∠EMA=60°,∴∠DMB=60°,过切点D作DF⊥AB于F点,∴MF=1,DF=,则直线PD过E(-1,2)、D(2, )的坐标代入,则函数PD的解析式为y=-.当点E在第三象限时,切点D在第四象限,同理可求直线PD的解析式为y=,因此直线PD的函数关系式为y=-或y=;
(3)若四边形EAMD的面积等于△DAN的面积,又S四边形EAMD=2S△EAM,S△DAN=2S△AMD,则S△EAM= S△AMD,∴E、D两点到x轴的距离相等,∵PD与⊙M相切,∴点D与点E在x轴同侧,∴切线PD与x轴平行,此时切线PD的函数关系式为y=2或y
=-2,当y=2时,由y= x2-2x-3得,x=1±,当y=-2时,由y= x2-2x-3得,x=1±,故满足条件点P的位置有4个,分别是P1(1+,2)、P2(1-,2)、P3(1+,-2)、P4(1-,-2).
29.(2010湖南怀化)图9是二次函数的图象,其顶点坐标为M(1,-4).
(1)求出图象与轴的交点A,B的坐标;
(2)在二次函数的图象上是否存在点P,使,若存在,求出P点的
坐标;若不存在,请说明理由;
(3)将二次函数的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,
得到一个新的图象,请你结合这个新的图象回答:当直线与此
图象有两个公共点时,的取值范围.
图9
【答案】解;(1) 因为M(1,-4) 是二次函数的顶点坐标,
所以
令解之得.
∴A,B两点的坐标分别为A(-1,0),B(3,0)
(2) 在二次函数的图象上存在点P,使
设则,又,
∴
∵二次函数的最小值为-4,∴.当时,.故P点坐标为(-2,5)或(4,5)
图1
(3)如图1,当直线经过A点时,可得当直线经过B点时,可得由图可知符合题意的的取值范围为
30.(2010河南)在平面直角坐标系中,已知抛物线经过A(4,0),B(0,一4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、0为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
【答案】(1)设抛物线的解析式为y=ax2+bx+c(a≠0),则有
解得
∴抛物线的解析式y=x2+x﹣4
(2)过点M作MD⊥x轴于点D.设M点的坐标为(m,n).
则AD=m+4,MD=﹣n,n=m2+m-4 .
∴S = S△AMD+S梯形DMBO-S△ABO
= ( m+4) (﹣n)+(﹣n+4) (﹣m) -×4×4
= ﹣2n-2m-8
= ﹣2(m2+m-4) -2m-8
= ﹣m2-4m (-4< m < 0)
∴S最大值 = 4
(3)满足题意的Q点的坐标有四个,分别是:(-4 ,4 ),(4 ,-4),
(-2+,2-),(-2-,2+)
31.(2010黑龙江哈尔滨) 已知:在△ABC中AB=AC,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)如图1,当∠ABC=45°时,求证:AE=MD;
(2)如图2,当∠ABC=60°时,则线段AE、MD之间的数量关系为: 。
(3)在(2)的条件下延长BM到P,使MP=BM,连接CP,若AB=7,AE=,
求tan∠ACP的值.
【答案】(1)证明:如图1 连接AD
∵AB=AC BD=CD ∴AD⊥BC 又∵∠ABC=45°
∠ABE=∠DBM ∴△ABE∽△DBM
(2)AE=2MD
(3)解:如图2 连接AD、EP ∵AB=AC
∠ABC=60°D ∴△ABC为等边三角形
又∵D为BC中点 ∴AD⊥BC ∠DAC=30
BD=DC=AB
∵∠BAE=∠BDM ∠ABE=∠DBM
∴△ABE∽△DBM
∠AEB=∠DMB ∴EB=EBM 又∵BM=MP
∴EB=BP 又∵∠EBM=∠ABC=60°
∴△BEP为等边三角形
∴EM⊥BP ∴∠BMD=90° ∴∠AEB=90°
∵D为BC中点 M为PB中点 ∴DM//PC
∴∠MDB=∠PCB ∴∠EAB=∠PCB
过N作NH⊥AC,垂足为H
在
32.(2010江苏徐州)如图①,将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点 M处,点C落在点N处,MN与CD交于点P, 连接EP.
(1)如图②,若M为AD边的中点,
①,△AEM的周长=_____cm;
②求证:EP=AE+DP;
(2)随着落点M在AD边上取遍所有的位置(点M不与A、D重合),△PDM的周长是否发生变化?请说明理由.
【答案】
33.(2010 四川绵阳)如图,抛物线y = ax2 + bx + 4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,
△EFK的面积最大?并求出最大面积.
C
E
D
G
A
x
y
O
B
F
【答案】(1)由题意,得 解得,b =-1.
所以抛物线的解析式为,顶点D的坐标为(-1,).
(2)设抛物线的对称轴与x轴交于点M.因为EF垂直平分BC,即C关于直线EG的对称点为B,连结BD交于EF于一点,则这一点为所求点H,使DH + CH最小,即最小为
DH + CH = DH + HB = BD =. 而 .
∴ △CDH的周长最小值为CD + DR + CH =.
设直线BD的解析式为y = k1x + b,则 解得 ,b1 = 3.
所以直线BD的解析式为y =x + 3.
由于BC = 2,CE = BC∕2 =,Rt△CEG∽△COB,
得 CE : CO = CG : CB,所以 CG = 2.5,GO = 1.5.G(0,1.5).
同理可求得直线EF的解析式为y =x +.
联立直线BD与EF的方程,解得使△CDH的周长最小的点H(,).
(3)设K(t,),xF<t<xE.过K作x轴的垂线交EF于N.
则 KN = yK-yN =-(t +)=.
所以 S△EFK = S△KFN + S△KNE =KN(t + 3)+KN(1-t)= 2KN = -t2-3t + 5 =-(t +)2 +.
即当t =-时,△EFK的面积最大,最大面积为,此时K(-,).
51.(2010江苏 镇江)探索发现(本小题满分9分)
如图,在直角坐标系的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
【答案】
(1);(1分)
(2)
① (2分)
(3分)
② (4分)(注:不去绝
对值符号不扣分)
(3)[法一]若OB=BD,则
由①得 (5分)
[法二]若OB=BD,则B点在OD的中垂线CM上.
∴直线CM的函数关系式为, ③ (5分)
④
联立③,④得:,
[法三]若OB=BD,则B点在OD的中垂线CM上,如图27 – 1
过点B作
(4)如果,
①当,如图27 – 2
∴此时四边形BDCF为直角梯形.(7分)
②当如图27 – 3
∴此时四边形BDCF为平行四边形.(8分)
下证平行四边形BDCF为菱形:
[法一]在,
[方法①]上方
(舍去).
得
[方法②]由②得:
此时
∴此时四边形BDCF为菱形(9分)
[法二]在等腰中
52.(2010 四川泸州)已知二次函数及一次函数.
(1) 求该二次函数图象的顶点坐标以及它与轴的交点坐标;
(2) 将该二次函数图象在轴下方的部分沿轴翻折到轴上方,图象的其余部分不变,得到一个新图象.请你在图10中画出这个新图象,并求出新图象与直线
有三个不同公共点时的值;
(1) 当0≤≤2时,函数的图象与轴有两个不同公共点,求的取值范围.
【答案】解: (1),
则抛物线的顶点坐标为(1,)
∵的图象与轴相交,∴,
∴,∴,或,
∴抛物线与轴相交于A(,0)、B(3,0).
(2)翻折后所得新图象如图所示,平移直线知:直线位于和时,它与新图象有三个不同公共点,如图所示,
.
①当直线位于时,此时过点A(,0),
∴,即,
②当直线位于时,
此时与函数(≤≤3)的图象有一个公共点,
∴方程,即有一个根,
故△==0,即,
当时,满足≤≤3,
由①②知,,或
(3)∵,
∵当0≤≤2时,函数的图象与轴有两个不同交点,
∴应同时满足下列三个方面的条件:
方程的判别式△>0,
抛物线的对称轴满足<<2,
当时,函数值≥0,
当时,函数值≥0,
即
>0
0<<2
≥0
≥0
解得 ≤<1,
∴当≤<1时,函数图象(0≤≤2)
与轴有两个不同交点.
53.(2010 山东淄博)已知直角坐标系中有一点A(—4,3),点B在x轴上,△AOB是等腰三角形.
(1)求满足条件的所有点B的坐标;
(2)求过O,A,B三点且开口向下的抛物线的函数表达式(只需求出满足条件的一条即可);
(3)在(2)中求出的抛物线上存在点P,使得以O,A,B,P四点为顶点的四边形是梯形,求满足条件的所有点P的坐标及相应梯形的面积.
【答案】解:作AC⊥x轴,由已知得OC=4,AC=3,OA==5.
(1)当OA=OB=5时,
如果点B在x轴的负半轴上,如图(1),点B的坐标为(-5,0).
如果点B在x轴的正半轴上,如图(2),点B的坐标为(5,0).
x
y
B
C
A
O
x
y
B
C
A
O
(第24题)
(2)
(1)
当OA=AB时,点B在x轴的负半轴上,如图(3),BC=OC,则OB=8,点B的坐标为(-8,0).
当AB=OB时,点B在x轴的负半轴上,如图(4),在x轴上取点D,使AD=OA,可知OD=8.由∠AOB=∠OAB=∠ODA,可知△AOB∽△ODA,则,解得OB=,点B的坐标为(-,0).y
B
C
A
x
O
(3)
(4)
(第24题)
y
A
B
D
x
O
(2)当AB=OA时,抛物线过O(0,0),A(-4,3),B(-8,0)三点,设抛物线的函数表达式为,可得方程组,解得a=,,.
(当OA=OB时,同理得.
(3)当OA=AB时,若BP∥OA,如图(5),作PE⊥x轴,则∠AOC=∠PBE,∠ACO=∠PEB=90°,△AOC∽△PBE,.设BE=4m,PE=3m,则点P的坐标为(4m-8,-3m),代入,解得m=3.
则点P的坐标为(4,-9),
S梯形ABPO=S△ABO+S△BPO=48.
若OP∥AB(图略),根据抛物线的对称性可得点P的坐标为(-12,-9),
S梯形AOPB=S△ABO+S△BPO=48.
(第24题)
(5)
O
y
B
C
A
x
P
E
(6)
x
y
B
A
O
C
P
(第24题)
F
(当OA=OB时,若BP∥OA,如图(6),作PF⊥x轴,则∠AOC=∠PBF,∠ACO=∠PFB=90°,△AOC∽△PBF,.设BF=4m,PF=3m,则点P的坐标为(4m-5,-3m),代入,解得m=.
则点P的坐标为(1,-),
S梯形ABPO=S△ABO+S△BPO=.
若OP∥AB(图略),作PF⊥x轴,则∠ABC=∠POF,∠ACB=∠PFO=90°,△ABC∽△POF,.设点P的坐标为(-n,-3n),代入,解得n=9.则点P的坐标为(-9,-27),S梯形AOPB=S△ABO+S△BPO=75.
54.(2010 天津) 在平面直角坐标系中,已知抛物线与轴交于点、(点在点的左侧),与轴的正半轴交于点,顶点为.
(Ⅰ)若,,求此时抛物线顶点的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点恰好落在直线上,求此时抛物线的解析式.
【答案】解:(Ⅰ)当,时,抛物线的解析式为,即.
∴ 抛物线顶点的坐标为(1,4). .................2分
(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点在对称轴上,有,
∴ 抛物线的解析式为().
∴ 此时,抛物线与轴的交点为,顶点为.
∵ 方程的两个根为,,
∴ 此时,抛物线与轴的交点为,.
E
y
x
F
B
D
A
O
C
如图,过点作EF∥CB与轴交于点,连接,则S△BCE = S△BCF.
∵ S△BCE = S△ABC,
∴ S△BCF = S△ABC.
∴ .
设对称轴与轴交于点,
则.
由EF∥CB,得.
∴ Rt△EDF∽Rt△COB.有.
∴ .结合题意,解得 .
∴ 点,.
设直线的解析式为,则
解得
∴ 直线的解析式为. .........................6分
(Ⅲ)根据题意,设抛物线的顶点为,(,)
则抛物线的解析式为,
此时,抛物线与轴的交点为,
与轴的交点为,.()
过点作EF∥CB与轴交于点,连接,
则S△BCE = S△BCF.
由S△BCE = 2S△AOC,
∴ S△BCF = 2S△AOC. 得.
设该抛物线的对称轴与轴交于点.
则 .
于是,由Rt△EDF∽Rt△COB,有.
∴ ,即.
结合题意,解得 . ①
∵ 点在直线上,有. ②
∴ 由①②,结合题意,解得.
有,.
∴ 抛物线的解析式为. .........................10分
55.(2010广西桂林)如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,
FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
H
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.[来源:Zxxk.Com]
【答案】证明(1)连结OF
H
∵FH是⊙O的切线
∴OF⊥FH ……………1分
∵FH∥BC ,
∴OF垂直平分BC ………2分
∴
∴AF平分∠BAC …………3分
(2)证明:由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2 ……………4分
H
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3 ……………5分
∠FDB=∠FBD
∴BF=FD ………………6分
(3)解: 在△BFE和△AFB中
∵∠5=∠2=∠1,∠F=∠F
∴△BFE∽△AFB ………………7分
∴, ……………8分
∴
∴ ……………………9分
∴
∴AD== …………………10分
56.(2010湖北十堰)(本小题满分10分)已知关于x的方程mx2-(3m-1)x+2m-2=0
(1)求证:无论m取任何实数时,方程恒有实数根.
(2)若关于x的二次函数y= mx2-(3m-1)x+2m-2的图象与x轴两交点间的距离为2时,求抛物线的解析式.
(3)在直角坐标系xoy中,画出(2)中的函数图象,结合图象回答问题:当直线y=x+b与(2)中的函数图象只有两个交点时,求b的取值范围.
【答案】解:(1)分两种情况讨论:
①当m=0 时,方程为x-2=0,∴x=2 方程有实数根
②当m≠0时,则一元二次方程的根的判别式
△=[-(3m-1)]2-4m(2m-2)=m2+2m+1=(m+1)2≥0
不论m为何实数,△≥0成立,∴方程恒有实数根
综合①②,可知m取任何实数,方程mx2-(3m-1)x+2m-2=0恒有实数根.
(2)设x1,x2为抛物线y= mx2-(3m-1)x+2m-2与x轴交点的横坐标.
则有x1+x2=,x1·x2=
由| x1-x2|====,
由| x1-x2|=2得=2,∴或
∴m=1或m=
∴所求抛物线的解析式为:y1=x2-2x或y2=x2+2x-
即y1= x(x-2)或y2=(x-2)(x-4)其图象如右图所示.
(3)在(2)的条件下,直线y=x+b与抛物线y1,y2组成的图象只有两个交点,结合图象,求b的取值范围.
,当y1=y时,得x2-3x-b=0,△=9+4b=0,解得b=-;
同理,可得△=9-4(8+3b)=0,得b=-.
观察函数图象可知当b<-或b>-时,直线y=x+b与(2)中的图象只有两个交点.
由
当y1=y2时,有x=2或x=1
当x=1时,y=-1
所以过两抛物线交点(1,-1),(2,0)的直线y=x-2,
综上所述可知:当b<-或b>-或b=-2时,直线y=x+b与(2)中的图象只有两个交点.
57.(2010 四川自贡)如图,在直角坐标平面内,O为坐标原点,A点的坐标为(1,0),B点在x轴上且在点A的右侧,AB=OA,过点A和B作x轴的垂线分别交二次函数y=x2的图象于点C和D,直线OC交BD于M,直线CD交y轴于点H。记C、D的横坐标分别为xC,xD,点H的纵坐标yH。
(1)证明:①S△CMD∶S梯形ABMC=2∶3
②xC·xD=-yH
(2)若将上述A点坐标(1,0)改为A点坐标(t,0),t>0,其他条件不变,结论S△CMD:S梯形ABMC=2∶3是否仍成立?请说明理由。
(3)若A的坐标(t,0)(t>0),又将条件y=x2改为y=ax2(a>0),其他条件不变,那么XC、XD和yH又有怎样的数量关系?写出关系式,并证明。
【答案】 全品中考网
58.(2010宁夏回族自治区)在△ABC中,∠BAC=45°,AD⊥BC于D,将△ABD沿AB所在的直线折叠,使点D落在点E处;将△ACD沿AC所在的直线折叠,使点D落在点F处,分别延长EB、FC使其交于点M.
(1)判断四边形AEMF的形状,并给予证明.
(2)若BD=1,CD=2,试求四边形AEMF的面积.
【答案】解:(1)∵ADBC
△AEB是由△ADB折叠所得
∴∠1=∠3,∠E=∠ADB=,BE=BD, AE=AD
又∵△AFC是由△ADC折叠所得
∴∠2=∠4,∠F=∠ADC=,FC=CD,AF=AD
∴AE=AF---------------------------------------------2分
又∵∠1+∠2=,
∴∠3+∠4=
∴∠EAF=--------------------------------------3分
∴四边形AEMF是正方形。---------------------5分
(2)方法一:设正方形AEMF的边长为x
根据题意知:BE=BD, CF=CD
∴BM=x-1; CM=x-2-------------------------------------------------------------------7分
在Rt△BMC中,由勾股定理得:
∴
解之得: (舍去)
∴------------------------------------------10分
方法二:设:AD=x
∴=
∴-----------------------------------------------------------7分
∵
且
∴ 即
解之得: (舍去)
∴---------------------------------------------10分
59.(2010吉林长春)如图①,在平面直角坐标系中,等腰直角△A0B的斜边OB在x轴上,顶点A的坐标为(3,3),AD为斜边上的高.抛物线与直线交于点O、C,点C的横坐标为6。点P在x轴的正半轴上,过点P作PE//y轴,交射线OA于点E.设点P的横坐标为m,以A、B、D、E为顶点的四边形的面积为S.
(1)求OA所在直线的解析式.(1分)
(2)求a的值.(2分)
(3)当m≠3时.求S与m的函数关系式.(4分)
(4)如图②.设直线PE交射线0C于点R,交抛物线于点Q.以RQ为一边,在RQ的右侧作矩形RQMN,其中RN .直接写出矩形RQMN与△AOB重叠部分为轴对称图形时m的取值范围.(3分)
【答案】
60.(2010广东茂名)已知⊙O1的半径为R,周长为C.
(1)在⊙O1内任意作三条弦,其长分别是、、.求证:++< C; (3分)
(第25题(1)图)
(第25题备用图)
(2)如图,在直角坐标系O中,设⊙O1的圆心为O1.
①当直线:与⊙O1相切时,求的值;(2分)
②当反比例函数的图象与⊙O1有两个交点时,
求的取值范围. (3分)
(第25题备用图)
:
【答案】(1)证明:,,.++,
因此,++< C.
(2)解:①如图,根据题意可知⊙O1与轴、轴分别相切,设直线与⊙O1相切于点M,则O1M⊥l,过点O1作直线NH⊥轴,与交于点N,与轴交于点H,又∵直线与轴、轴分别交于点E(,0)、F(0,),∴OE=OF=,∴∠NEO=45o,∴∠ENO1=45o,在Rt△O1MN中,O1N=O1Msin45o=,
∴点N的坐标为N(R,),
把点N坐标代入得:,解得:,
②如图,设经过点O、O1的直线交⊙O1于点A、D,则由已知,直线OO1:是圆与反比例函数图象的对称轴,当反比例函数的图象与⊙O1
直径AD相交时(点A、D除外),则反比例函数的图象与⊙O1有两个交点.
过点A作AB⊥轴交轴于点B,过O1作O1C⊥轴于点C,OO1=O1Csin45o=,OA=,所以OB=AB=sin45o=,
因此点A的坐标是A,将点A的坐标 代入,解得:.
同理可求得点D的坐标为D,
将点D的坐标代入,解得:
所以当反比例函数的图象与⊙O1有两个交点时,的取值范围是:
61.(2010辽宁大连)如图17,抛物线F:与轴相交于点C,直线经过点C且平行于轴,将向上平移t个单位得到直线,设与抛物线F的交点为C、D,与抛物线F的交点为A、B,连接AC、BC
(1)当,,,时,探究△ABC的形状,并说明理由;
(2)若△ABC为直角三角形,求t的值(用含a的式子表示);
(3)在(2)的条件下,若点A关于轴的对称点A’恰好在抛物线F的对称轴上,连接A’C,BD,求四边形A’CDB的面积(用含a的式子表示)
O
C
A
B
D
x
图17
【答案】
62.(2010贵州遵义)如图,在⊿ABC,∠C= 90��������°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC、BC相切于点D、E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=χ,⊙O的半径为y,求y与χ的函数关系式。
【答案】【答案】解法一:连接OD、OE、OC……………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE…………………………………2分
∵S△ABC=S△AOC+S△BOC
∴AC×BC=AC×OD+BC×OE ……………………3分
∵AC+BC=8,AC =2,∴BC=6
∴×2×6=×2×OD+×2×OE ……………………4分
而OD=OE,∴OD=,即⊙O的半径为 ………………5分
解法二:连接OD、OE ………………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE ……………………………2分
∴∠C=90°,∴OECD为正方形
∴OD=OE=EC=CD=t ………………………3分
而△AOD∽△ABC,∴ ………………………4分
∵AC+BC=8,AC =2,∴BC=6,AD=2-t
∴,r=,即⊙O的半径为………………………5分
(2)(7分)连接OD、OE、OC ……………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE=y ………………………2分
S△ABC=S△AOC+S△BOC
∴AC×BC=AC×OD+BC×OE ……………………3分
∵AC+BC=8,AC =x,∴BC=8-x ………………………………4分
x(8-x)=xy+(8-x)y ………………………………5分
化简:8x-x2=xy+8y-xy………………………………………6分
即:y=-x2+x ………………………………………………7分
解法二:连接OD、OE ………………………………………1分
∵D、E为切点,
∴OD⊥AC,OE⊥BC,OD=OE ………………………2分
∴∠C=90°,∴OECD为正方形
∴OD=OE=EC=CD=y ………………………………3分
由OD∥BC,∴△AOD∽△ABC,
(或者:OD∥AC,∴△OBE∽△ABC)
∴.
∵AC+BC==8,AC=x,
∴BC=8-x,AD=AC-CD=x-y.
∴.
化简得:xy=(x-y)(8-x),
xy=8x-x2-8y+xy.
所以.
解法三:连接OD、OE.
∵D,E是切点,
∴OD⊥AC,OE⊥BC,OD=OE.
∵∠C=90°,∴OECD是正方形.
∴OD=OE=EC=CD=y.
由OD∥BC得:△AOD∽△ABC,
∴,即 ①.
由OE∥AC得:△BOE∽△BAC,
∴,即 ②.
①+②得:,
即.
∴.
63.(2010湖北宜昌)如图①,P是△ABC边AC上的动点,以P为顶点作矩形PDEF,顶点D,E在边BC上,顶点F在边AB上;△ABC的底边BC及BC上的高的长分别为a , h,且是关于x的一元二次方程的两个实数根,设过D,E,F三点的⊙O的面积为,矩形PDEF的面积为。
(1)求证:以a+h为边长的正方形面积与以a、h为边长的矩形面积之比不小于4;
(2)求的最小值;
(3)当的值最小时,过点A作BC的平行线交直线BP与Q,这时线段AQ的长与m , n , k的取值是否有关?请说明理由。(11分)
A
C
B
(第23题)
解:解法一:
(1)据题意,∵a+h=.
∴所求正方形与矩形的面积之比:
1分
由知同号,
2分
(说明:此处未得出只扣1分, 不再影响下面评分)
3分
即正方形与矩形的面积之比不小于4.
(2)∵∠FED=90º,∴DF为⊙O的直径.
⊙
∴⊙O的面积为:. 4分
矩形PDEF的面积:.
⊙
∴面积之比: 设
⊙
……………………………………………………………6分
,
⊙
,即时(EF=DE), 的最小值为 7分
⊙
(3)当的值最小时,这时矩形PDEF的四边相等为正方形.
过B点过BM⊥AQ,M为垂足,BM交直线PF于N点,设FP= e,
∵BN∥FE,NF∥BE,∴BN=EF,∴BN =FP =e.
由BC∥MQ,得:BM =AG =h.
∵AQ∥BC, PF∥BC, ∴AQ∥FP,
∴△FBP∽△ABQ. 8分
M
N
(说明:此处有多种相似关系可用,要同等分步骤评分)
∴,……9分
∴.∴……10分
……11分
∴线段AQ的长与m,n,k的取值有关.
(解题过程叙述基本清楚即可)
解法二:
(1)∵a,h为线段长,即a,h都大于0,
∴ah>0…………1分(说明:此处未得出只扣1分,再不影响下面评分)
∵(a-h)2≥0,当a=h时等号成立.
故,(a-h)2=(a+h)2-4a h≥0. 2分
∴(a+h)2≥4a h,
∴≥4.(﹡) 3分
这就证得≥4.(叙述基本明晰即可)
(2)设矩形PDEF的边PD=x,DE=y,则⊙O的直径为 .
S⊙O=…………4分, S矩形PDEF=xy
⊙
=
= 6分
由(1)(*), .
.
⊙
∴的最小值是 7分
⊙
(3)当的值最小时,
这时矩形PDEF的四边相等为正方形.
∴EF=PF.作AG⊥BC,G为垂足.
∵△AGB∽△FEB,∴.……8分
∵△AQB∽△FPB, ,……9分
∴=.
而 EF=PF,∴AG=AQ=h, ……………10分
∴AG=h=,
或者AG=h= 11分
∴线段AQ的长与m,n,k的取值有关.
64.(2010湖北宜昌)如图,直线y=hx+d与x轴和y轴分别相交于点A(-1,0),B(0,1),与双曲线y=在第一象限相交于点C;以AC为斜边、为内角的直角三角形,与以CO为对角线、一边在x轴上的矩形面积相等;点C,P在以B为顶点的抛物线y=上;直线y=hx+d、双曲线y=和抛物线同时经过两个不同的点C,D。
(1)确定t的值
(2)确定m , n , k的值
(3)若无论a , b , c取何值,抛物线都不经过点P,请确定P的坐标
(12分)
(第24题)
【答案】(1)直线过点A,B,则0=-h+d和1=d,即y=x+1. 1分
双曲线y=经过点C(x1,y1),x1y1=t.
以AC为斜边,∠CAO为内角的直角三角形的面积为×y1×(1+x1);
以CO为对角线的矩形面积为x1y1,
×y1×(1+x1)=x1y1,因为x1,y1都不等于0,故得x1=1,所以y1=2.
故有,,即t=2. 2分
(2)∵B是抛物线y=mx2+nx+k的顶点,∴有- ,
得到n=0,k=1. 3分
∵C是抛物线y=mx2+nx+k上的点,∴有2=m(1)2+1,得m=1. 4分
(3)设点P的横坐标为p,则纵坐标为p2+1.
∵抛物线y=ax2+bx+c经过两个不同的点C,D,
其中求得D点坐标为(-2,-1). 5分.
解法一:
故 2=a+b+c,
-1=4a-2b+c.
解之得,b=a+1, c=1-2a. 6分
(说明:如用b表示a,c,或用c表示a,b,均可,后续参照得分)
∴y=ax2+( a+1)x+(1-2a )
于是: p2+1≠a p2+(a+1)p+(1-2a) 7分
∴无论a取什么值都有p2-p≠(p2+p-2)a. 8分[来源:学+科+网Z+X+X+K]
(或者,令p2-p=(p2+p-2)a 7分
∵抛物线y=ax2+bx+c不经过P点,
∴此方程无解,或有解但不合题意 8分)
.
故∵a≠0,∴①
解之p=0,p=1,并且p≠1,p≠-2.得p=0. 9分
∴符合题意的P点为(0,1). …………10分
②,解之p=1,p=-2,并且p≠0,p≠1.
得p=-2. 11分
符合题意的P点为(-2,5). 12分
∴符合题意的P点有两个(0,1)和(-2,5).
解法二:
则有(a-1)p2+(a+1) p-2a=0 7分
即〔(a-1)p+2a〕(p-1)=0
有p-1=0时,得p=1,为(1,2)此即C点,在y=ax2+bx+c上. 8分
或(a-1)p+2a=0,即(p+2)a=p
当p=0时a=0与a≠0矛盾 9分
得点P(0,1) 10分
或者p=-2时,无解 11分[来源:学科网]
得点P(-2,5) 12分
故对任意a,b,c,抛物线y=ax2+bx+c都不经过(0,1)和(-2,5)
解法三:
如图, 抛物线y=ax2+bx+c不经过直线CD上除C,D外的其他点.
(只经过直线CD上的C,D点). 6分
由 7分
解得交点为C(1,2),B(0,1).
故符合题意的点P为(0,1). 8分
抛物线y=ax2+bx+c不经过直线x=-2上除D外的其他点. 9分
65.(2010 福建莆田)如图1,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD= 。
(1).求直线AC的解析式;
(2).在y轴上是否存在点p,直线PD与矩形对角线AC交于点M,使得△DMC为等腰三角形?若存在,直接写出所有符合条件的点p的坐标;若不存在,请说明理由。
(3).抛物线y= 经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且△ODE沿DE折叠后点O落在边AB上 处?
【答案】【答案】
【答案】
66.(2010广西河池)如图11,在直角梯形中,∥,,点为坐标原点,点在轴的正半轴上,对角线,相交于点,,.
(1)线段的长为 ,点的坐标为 ;
(2)求△的面积;
(3)求过,,三点的抛物线的解析式;
(4)若点在(3)的抛物线的对称轴上,点为该
抛物线上的点,且以,,,四点为顶点的四边形
为平行四边形,求点的坐标.
M
C
B
O
A
图11
【答案】解:(1)4 ;.
(2)在直角梯形OABC中,OA=AB=4,
∵ ∥ ∴ △OAM∽△BCM 又 ∵ OA=2BC
∴ AM=2CM ,CM=AC 所以
(注:另有其它解法同样可得结果,正确得本小题满分.)
(3)设抛物线的解析式为
由抛物线的图象经过点,,.所以
解这个方程组,得,,
所以抛物线的解析式为
(4)∵ 抛物线的对称轴是CD,
① 当点E在轴的下方时,CE和OA互相平分则可知四边形OEAC为平行四边形,此时点F和点C重合,点F的坐标即为点;
② 当点E在轴的下方,点F在对称轴的右侧,存在平行四边形,∥,且,此时点F的横坐标为6,将代入,可得.所以.
同理,点F在对称轴的左侧,存在平行四边形,∥,且,此时点F的横坐标为,将代入,可得.所以.(12分)
综上所述,点F的坐标为,.
67.(2010广东肇庆)已知二次函数的图象过点(2,1)
(1)求证:
(2)求的最大值
(3)若二次函数的图象与轴交于点,,,,的面积是,求
【答案】解:(1)∵的图象过点(2,1)
∴
∴
(2)
当时,
此时,
∴当时,有最大值,最大值为2。
(3)由根与系数关系可知:,
,
当或时,
∴的面积是时,或
68.(2010内蒙呼和浩特)在平面直角坐标系中,函数y=(x>0,m是常数)的图像经过点A(1,4)、点B(a,b),其中a>1.过点A作x中的垂线,垂足为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点M,连结AD、DC、CB与AB.
(1)求m的值;
(2)求证:DC∥AB;
(3)当AD=BC时,求直线AB的函数解析式.
【答案】解:(1)∵点A(1,4)在函数y=的图像上,
∴4=,得m=4.……………………………2分
(2)∵点B(a,b)在函数y=的图像上,∴ab=4.
又∵AC⊥x轴于C,BD⊥y轴于D交AC于M,∴AC⊥BD于M
∴M(1,b),D(0,b),C(1,0)
∴tan∠BAC====,tan∠DCM==……………4分
∴tan∠BAC =tan∠DCM,
所以锐角∠BAC=∠DCM,DC∥AB………………………………………………6分
说明:利用两边对应成比例且夹角相等的三角形相似,易证△ABM∽△CDM,易得∠BAC=∠DCM.评分标准为证出相似得到4分,证出平行得到6分.
(3)设直线AB的解析式为y=kx+b
∵AB∥CD,AD=BC,∴四边形ABCD是平行四边形或等腰梯形.
① 四边形ABCD是平行四边形时,AC与BD互相平分,
又∵AC⊥BD,∴B(2,2)
∴,解得
∴直线AB的解析式为:y=-2x+6.………………8分
②当四边形ABCD是等腰梯形时,
BD与AC相等且垂直,∵AC=BD=4,
∴B(4,1)
∴同理可求直线AB的解析式为y=-x+5.…………………10分
69.(2010四川攀枝花)如图12,在矩形ABCD中,AB=6,AD=2,点P是边BC上的动点(点P不与点B、C重合),过点P作直线PQ∥BD,交CD边于Q点,再把△PQC沿着动直线PQ对折,点C的对应点是R点。设CP=x, △PQR与矩形ABCD重叠部分的面积为y。
(1)求∠CPQ的度数。
(2)当x取何值时,点R落在矩形ABCD的边AB上?
(3)当点R在矩形ABCD外部时,求y与x的函数关系式。并求此时函数值y的取值范围。
F
E
图12(2)
P
D
C
Q
A
B
R
B
图12(1)
P
R
Q
A
C
D
【答案】解:
(1)∵四边形ABCD是矩形 ∴AB=CD,AD=BC 又AB=6,AD=2,∠C=90°
∴CD=6,BC=2 ∴tan∠CBD== ∴∠CBD=60°
∵PQ∥BD ∴∠CPQ=∠CBD=60°………………………2分
(2)如题图12(1)由轴对称的性质可知△RPQ≌△CPQ
∴∠RPQ=∠CPQ,RP=CP.由(1)知∠RPQ=∠CPQ=60° ∴∠RPB=60°,∴RP=2BP
∵CP=x ∴RP=x ,PB=2-x. ………………………4分
∴在△RPB中,有2(2-x)= x ∴x=………………6分
(3)当R点在矩形ABCD的外部时(如题图12(2)),﹤x﹤2
在Rt△PBF中,由(2)知PF=2BP=2(2-x)
∴RP=CP=x ∴ER=RF-PF=3x-4………………………7分
在Rt△ERF中 ∵∠EFR=∠PFB=30° ∴ER=RF·tan30°=x-4
∴S△ERF=ER×FR=(x-4)( 3x-4)=-12x+8………8分
又S△PQR=S△CPQ=x×x=
∵y=S△PQR-S△ERF ∴当﹤x﹤2时,函数的解析式为
y=-(-12x+8)
=-+12x-8 (﹤x﹤2)…………10分
∵y=-+12x-8 =-(x-2)+4
∴当﹤x﹤2时,y随x的增大而增大
∴函数值y的取值范围是﹤y﹤4…………12分
70.(2010湖北黄石)在△ABC中,分别以AB、BC为直径⊙O、⊙O,交于另一点D.
⑴证明:交点D必在AC上;
⑵如图甲,当⊙O与⊙O半径之比为4︰3,且DO与⊙O相切时,判断△ABC的形状,并求tan∠ODB的值;
⑶如图乙,当⊙O经过点O,AB、DO的延长线交于E,且BE=BD时,求∠A的度数.
【答案】
y
x
由 10分
解得交点P为(-2,5).……11分
抛物线y=ax2+bx+c不经过直线x=1上除C外的其他点,
而解得交点为C(1,2). ……12分
故符合条件的点P为(0,1)或(-2,5).