- 2021-05-13 发布 |
- 37.5 KB |
- 53页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
20062015陕西中考数学真题分类整理
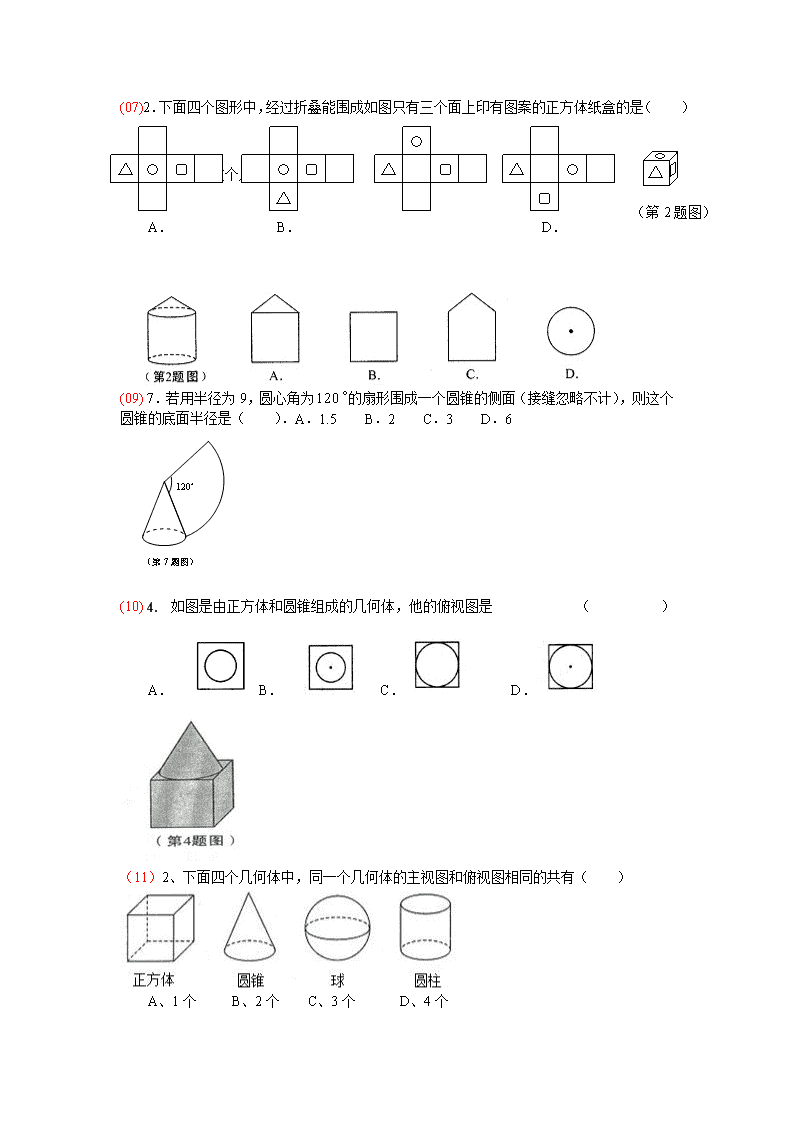
1、 主考初一引入的负数知识,同时里边又用倒数、相反数、绝对值、零次方、相反数的意 义去考察。(必考题) (06)1.下列计算正确的是 ( ) A. B. C. D. (07)1. 的相反数为 ( ) A.2 B. C. D. (08)1、零上 13℃记作+13℃,零下 2℃可记作 ( ) A.2 B.-2 C. 2℃ D.-2℃ (09)1. 的倒数是( ) A.2 B. C. D. (10) 1. ( ) A. 3 B-3 C D- (11)1、 的倒数为( ) A、 B、 C、 D、 (12)1.如果零上 5 ℃记做+5 ℃,那么零下 7 ℃可记作( ) A.-7 ℃ B.+7 ℃ C.+12 ℃ D.-12 ℃ (13)1.下列四个数中最小的数是( )A.-2 B.0 C. D.5 (14)11.计算(- 1 3)-2 = . (15)1.计算(- 2 3)0=( )A. 1 B. - 2 3 C. 0 D. 2 3 2、考察组合体的三视图,或展开图中的邻居和对门的试题(必考题) (06)2.如图,几何体的左视图是 【 】 3 1− 123 =+− 22 −=− 9)3(3 −=−× 1120 =− 2− 2− 1 2 1 2 − 1 2 − 2− 1 2 1 2 − 1 3 − = 1 3 1 3 120° (第 7 题图) (07)2.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是( ) (08)2、如图,这个几何体的主视图是 ( ) (09) 7.若用半径为 9,圆心角为 的扇形围成一个圆锥的侧面(接缝忽略不计),则这个 圆锥的底面半径是( ).A.1.5 B.2 C.3 D.6 (10) 4. 如图是由正方体和圆锥组成的几何体,他的俯视图是 ( ) A. B. C. D. (11)2、下面四个几何体中,同一个几何体的主视图和俯视图相同的共有( ) A、1 个 B、2 个 C、3 个 D、4 个 120° A. B. D. (第 2 题图) (12)2.如图,是由三个相同的小正方体组成的几何体,该几何体的左视图是( ) (13)2.如图,下面的几何体是由一个圆柱和一个长方体组成的,则它的俯视图是( ) (14)2.下图是一个正方体被截去一个直三棱柱得到的几何体,则该几何体的左视图是 ( ) (15)2.如图是一个螺母的示意图,它的俯视图是( ) A. B. C. D. 3、不等式、不等式组和不等式组解集的表示(2011 版的数学课程标准下,不在考察不等式 组的应用) (06) 11.不等式 的解集为 。 (07)3.不等式组 的解集是( ) A. B. ,或 C. D. (08)4、把不等式组 的解集表示在数轴上,正确的是 ( ) (09)6.如果点 在第四象限,那么 m 的取值范围是( ). )1(32 +≤− xx 2 5−≥x 2 0 3 0 x x + > − , ≥ 2 3x− ≤ ≤ 2x < − 3x≥ 2 3x− < < 2 3x− < ≤ x 3 1 5 x 6 − <- - < ( 1 2 )P m m−, A. B. C. D. (第 2 题图) A B C D A. B. C. D. A. B. C. D. (10) 7. 不等式组 的解集是 A -1< x≤2 B -2≤x<1 C x<-1 或 x≥2 D 2≤x<-1 (13)4.不等式组 的解集为( ) A. > B. <-1 C. -< < D. >- (14)5.把不等式组 的解集表示在数轴上,正确的是( ) (15)7.不等式组 的最大整数解为( )A. 8 B. 6 C.5 D. 4 4、科学计数法的考察(07、08、10、12、13、14、15 年没有具体考察,该考点近几年已经 不考)必考的知识点为——两直线位置关系(题位以前在填空题、前移到到选择题的位置) (06) 12.选做题(要求在(1)、(2)中任选一题作答)。 (1)2005 年 11 月 1 日零时,全国总人口为 130628 万人,60 岁及以上的人口占总人口的 11.03%,则全国 60 岁及以上的人口用科学记数法表示约为 万人(用计算器 计算,保留 3 个有效数字)。 (2)用计算器比较大小: 0(填 ) (09)2.1978 年,我国国内生产总值是 3 645 亿元,2007 年升至 249 530 亿元.将 249 530 亿 元用科学记数表示为( ). A. 元 B. 元 C. 元 D. 元 (11)3、我国第六次人口普查显示,全国人口为 1370536875 人,将这个总人口数(保留三 − − 321 02 1 x x x 2 1 x x 2 1 x 2 1 10 2m< < 1 02 m− < < 0m < 1 2m > 3 2 1x ≥ + > − 11- x 0, 2 2 1 3 0 x x + > − ≥ 1 1 32 2( 3) 0 x x x + ≥ − − − > 41044.1 × 6173 − ””、“”、““ = 1324.953 10× 1224.953 10× 132.4953 10× 142.4953 10× (第 3 题图) DC BA -1 1 2 30 -1 1 2 30 -1 1 2 300 321-1 个有效数字)用科学记数法表示为( ) A、1.37×109 B、1.37×107 C、1.37×108 D、1.37×1010 5、数据的统计:中位数、众数、平均数,方差、极差、标准差的考察。(必考题 15 年该小 题被删掉了,但该知识点依然在大题中体现) (06)5.如图是某市 5 月 1 日至 5 月 7 日每天最高、最低气温的折线统计图,在折 7 天中, 日温差最大的一天市 A.5 月 1 日 B.5 月 2 日 C.5 月 3 日 D.5 月 5 日 (07)4.将我省某日 11 个市、区的最高气温统计如下: 最高气温 10 14 21 22 23 24 25 26 市、区个数 1 1 3 1 1 2 1 1 该天这 11 个市、区最高气温的平均数和众数分别是( ) A. B. C. D. (08)5、在“爱的奉献”抗震救灾大型募捐活动中,文艺工作者积极向灾区捐款。其中 8 位 工作者的捐款分别是 5 万,10 万,10 万,10 万,20 万,20 万,50 万,100 万。这组数据 的众数和中位数分别是 ( ) A.20 万、15 万 B.10 万、20 万 C.10 万、15 万 D.20 万、10 万 (09)4.王老师为了了解本班学生课业负担情况,在班中随机调查了 10 名学生,他们每人上 周平均每天完成家庭作业所用的时间分别是(单位:小时):1.5,2,2,2,2.5,2.5,2.5, 2.5,3,3.5.则这 10 个数据的平均数和众数分别是( ). A.2.4,2.5 B.2.4,2 C.2.5,2.5 D.2.5,2 (10) 6. 中国 2010 年上海世博会充分体现“城市,让生活更美好”的主题。据统计 5 月 1 日至 5 月 7 日入园数(单位:万人)分别为 20.3, 21.5 13.2, 14.6, 10.9, 11.3, 13.9。 这组数据中的中位数和平均数分别为 A 14.6 ,15.1 B 14.65 ,15.0 C 13.9 , 15.1 D13.9 , 15.0 (11)6、某校男子男球队 10 名队员的身高(厘米)如下:179,182,170,174,188, 172,180,195,185,182,则这组数据的 中位数和众数分别是( ) A、181,181 B、182,181 C、180,182 D、181,182 (12)4.某中学举行歌咏比赛,以班为单位参赛,评委组的各位评委给九年级三班的演唱打 分情况(满分 100 分)如下表,从中去掉一个最高分和一个最低分,则余下的分数的平均分 是( ) 分数(分) 89 92 95 96 97 ℃ ℃ ℃ ℃ ℃ ℃ ℃ ℃ 21 21℃, ℃ 20 21℃, ℃ 21 22℃, ℃ 20 22℃, ℃ 评委(位) 1 2 2 1 1 A.92 分 B.93 分 C.94 分 D.95 分 (13)5.我省某市五月份第二周连续七天的空气质量指数分别为:111,96,47,68,70,77, 105.则这七天空气质量指数的平均数是( )A.71.8 B.77 C.82 D.95.7 (14)6 . 某 区 10 名 学 生 参 加 实 际 汉 字 听 写 大 赛 , 他 们 得 分 情 况 如 下 表 : ( ) 人数 3 4 2 1 分数 80 85 90 95 那么 10 名学生所得分数的平均数和众数分别是 A.85 和 82.5 B. 85.5 和 85 C. 85 和 85 D. 85.5 和 80 (08) 11、若∠α=43°,则∠α的余角的大小是 。 (09) 12.如图, ,直线 分别交 于点 , ,则 的 大小是__________. (10) 如 果 , 点 o 在 直 线 AB 上 且 AB ⊥ OD 若 ∠ COA=36 ° 则 ∠ DOB 的 大 小 为 ( ) A 3 6° B 54° C 64° D 72° (11)12、如图,AC∥BD,AE 平分∠BAC 交 BD 于点 E,若∠1=64°,则∠2= 122° . (13)3.如图,AB∥CD,∠CED=90°,∠AEC=35°,则∠D 的大小为( ) A.65° B.55° C.45° D.35° 6、(1)圆锥的侧面展开图:底面圆的半径和周长、母线长、圆锥的高、扇形的面积。利用三 个公式;(2)圆与圆的位置关系问题;(3)直线与圆的位置关系问题在选择题、填空题中的 考察(与 23 题互补,必考题) (06)4.如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,连接 CD,若⊙O 的半径 AB CD∥ EF AB CD、 E F、 1 47∠ = ° 2∠ A B DC E F 1 2 (第 12 题 图) E D B C A 120° (第 7 题图) (第 9 题图) A BC E F D O 第4题图 O A B D C , ,则 的值是 【 B 】 A. B. C. D. (06)6.若圆锥的侧面展开图市一个弧长为 的扇形,则这个圆锥的底面半径是 【 B 】 A.36 B.18 C.9 D.6 (07)6.如图,圆与圆之间不同的位置关系有( ) A.2 种 B.3 种 C.4 种 D.5 种 (08)9、如图,直线 AB 与半径为 2 的⊙O 相切于点 C,D 是⊙O 上一点,且∠EDC=30°,弦 EF∥AB,则 EF 的长度为 ( ) A.2 B. C. D. (09) 7.若用半径为 9,圆心角为 的扇形围成一个圆锥的侧面(接缝忽略不计),则这个 圆锥的底面半径是( ).A.1.5 B.2 C.3 D.6 (10) 9. 如图,点 A、B、P 在⊙O 上,且∠APB=50°,若点 M 是⊙O 上的动点,要使△ ABM 为等腰三角形,则所有符合条件的点 M 有 ( ) A 1 个 B 2 个 C 3 个 D 4 个 (10)14. 如图是一条水铺设的直径为 2 米的通水管道横截面,其水面宽 1.6 米,则这条管 道中此时最深为 米 (11)7、同一平面内的两个圆,他们的半径分别为 2 和 3,圆心距为 d,当 1<d<5 时,两 圆的位置关系是( )A、外离 B、相交 C、内切或外切 D、内含 (12)9.如图,在半径为 5 的圆 O 中,AB ,CD 是互相垂直的两条弦,垂足为 P,且 AB=CD=8,则 OP 的长为( )A.3 B.4 C. D. 7、正比例函数与一次函数的考察:(必考而且 12 年多了一道题,近几年维持在一正比例 和一反比例) (06)7.直线 与 轴、 轴所围成的三角形的面积为【 A 】 2 3=r 2=AC Bcos 2 3 3 5 2 5 3 2 π36 2 3 3 2 2 120° 3 2 24 32 3 +−= xy x y (07 第 6 题图) A.3 B.6 C. D. (07)7.如图,一次函数图象经过点 ,且与正比例函数 的 图象交于点 ,则该一次函数的表达式为( ) A. B. C. D. (08)8、如图,直线 AB 对应的函数表达式是 ( ) A. B. C. D. (09)5.若正比例函数的图象经过点( ,2),则这个图象必经过点( ). A.(1,2) B.( , ) C.(2, ) D.(1, ) (10) 5. 一个正比例函数的图像过点(2,-3),它的表达式为 ( ) A B C D (11)4、下列四个点,在正比例函数 的图象上的点是( ) A、(2,5) B、(5,2)C、(2,﹣5) D、(5,﹣2 (12)6.下列四组点中,可以在同一个正比例函数图象上的一组点是( ) A.(2.-3),(-4,6) B.(-2,3),(4,6) C.(-2,-3),(4,-6)D.(2,3),(-4, 6) (12)8.在同一平面直角坐标系中,若一次函数 图象交于点 ,则 点 的坐标为( )A.(-1,4) B.(-1,2) C.(2,-1) D.(2,1) (13)6.如果一个正比例函数的图象经过不同象限的两点 A(2,m)、B(n,3),那么一定有 ( )A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0 (13)8.根据下表中一次函数的自变量 与 的对应值,可得 P 的值为( ) -2 0 1 3 P 0 A.1 B.-1 C.3 D.-3 (14)3.若点 A(-2,m)在正比例函数 y= -1 2x 的图象上,则 m 的值是( ) A. 1 4 B.-1 4 C. 1 D.-1 (15)5.设正比例函数 y=mx 的图象经过点 A(m,4),且 y 的值随 x 值的增大而减小,则 m=( )A. 2 B. -2 C. 4 D. -4 (15)8.在平面直角坐标系中,将直线 l1:y= -2x-2 平移后,得到直线 l2:y= -2x+4,则下列 平移作法正确的是( ) A. 将 l1 向右平移 3 个单位长度 B. 将 l1 向右平移 6 个单位长度 C. 将 l1 向上平移 2 个单位长度 D. 将 l1 向上平移 4 个单位长度 8、应用题的考察(08、09 连续两年在选择题中没有考察;08 年加入了一个三角形和一个四 x y x y 4 3 2 3 A y x= − B 2y x= − + 2y x= + 2y x= − 2y x= − − 3y x 32 = − + 3y x 32 = + 2y x 33 = − + 2y x 33 = + 1− 1− 2− 1− 2− 3 2y x= − 2 3y x= 3 2y x= 2 3y x= − 533 −=+−= xyxy 与 M M (第 8 题图) x y O A B 2 3 O x y A B 1− y x= − 2 (第 7 题图) 第10题图 B D A G EF CP A D FC E B (第 9 题图) C O D P BA (第 10 题图) 边形;09 年加入了一个三角形的旋转,和一个分式的四则混合运算 11、12 年放在填空题中 考察) (06)9.有一块多边形草坪,在市政建设射击图纸上的面积为 300 ,其中一条边的长度为 5 ,经测量,这条边的实际长度为 15 ,则这块草坪的实际面积是 【 C 】 A.100 B.270 C.2700 D.90000 (07)5.中国人民银行宣布,从 2007 年 6 月 5 日起,上调人民币存款利率,一年定期存款利 率上调到 3.06%.某人于 2007 年 6 月 5 日存入定期为 1 年的人民币 5000 元(到期后银行将 扣除 20%的利息锐).设到期后银行应向储户支付现金 元,则所列方程正确的是( ) A. B. C、 D、 9、三角形和四边形的考察 (06)10.如图,矩形 ABCG( )与矩形 CDEF 全等,点 B、C、D 在同一条直线上, 的顶点 P 在线段 BD 上移动,使 为直角的点 P 的个数是 【 C 】 A.0 B.1 C.2 D.3 (08)6、如图,四边形 ABCD 的对角线互相平分,要使它变为矩形,需要添加的条件是( ) A.AB=CD B.AD=BC C.AB=BC D.AC=BD (10) 8. 若一个菱形的边长为 2,则这个菱形两条对角线的平方和为 ( ) A 16 B 8 C 4 D 1 (07)9.如图,在矩形 中, 为 的中点,连接 并延长交 的延长线于点 ,则图中全等的直角三角形共有( ) A.3 对 B.4 对 C.5 对 D.6 对 (07)10.如图,在等边 中, ,点 在 上,且 ,点 是 上一 动点,连结 ,将线段 绕点 逆时针旋转 得到线段 .要使点 恰好落在 上,则 的长是( )A.4 B.5 C.6 D.8 (09)9.如图, , 可以看作是由 绕点 顺时针 旋转 角度得到的.若点 在 上,则旋转角 的大小可以是( ). A. B. C. D. (10)13. 如图在△ABC 中 D 是 AB 边上一点,连接 CD,要使△ADC 与△ABC 相似,应 添加的条件是 (11)9、如图,在▱ABCD 中,E、F 分别是 AD、CD 边上的点,连接 BE、AF,他们相交 于 G,延长 BE 交 CD 的延长线于点 H,则图中的相似三角形共有( ) A、2 对 B、3 对 C、4 对 D、5 对 2cm cm m 2m 2m 2m 2m x 5000 5000 3.06%x − = × 5000 20% 5000 (1 3.06%)x + × = × + 5000 3.06% 20% 5000 (1 3.06%)x + × × = × + 5000 3.06% 20% 5000 3.06%x + × × = × BCAB APE∠ APE∠ ABCD E CD AE BC F ABC△ 9AC = O AC 3AO = P AB OP OP O 60 OD D BC AP 90 30AOB B∠ = ∠ =°, ° A OB′ ′△ AOB△ O α A′ AB α 30° 45° 60° 90° ( 第 6 题 图) A D CB O A O B A′ B′ ( 第 9 (11)5、在△ABC 中,若三边 BC,CA,AB 满足 BC:CA:AB=5:12:13,则 cosB= A、 B、 C、 D、 (12)5.如图,在 是两条中线,则 ( ) A.1∶2 B.2∶3 C.1∶3 D.1∶4 (12)7.如图,在菱形 中,对角线 与 相交于点 , ,垂足为 , 若 ,则 的大小为( ) A.75° B.65° C.55° D.50° (13)7.如图,在四边形 ABCD 中,AB=AD,CD=CB.若连接 AC、BD 相交于点 O,则图中全 等三角形共有( ) A.1 对 B.2 对 C.3 对 D.4 对 (13)9.如图,在矩形 ABCD 中,AD=2AB,点 M、N 分别在边 AD、BC 上, 连接 BM、DN.若四边形 MBND 是菱形,则 等于( ) A. B. C. D. (14)9.如图,在菱形 ABCD 中,AB=5,对角线 AC=6,过点 A 作 AE⊥BC,垂足为 E, 则 AE 的长为 ( ) A.4 B.12 5 C.24 5 D.5 (15)6. 如图,在△ABC 中,∠A=36°,AB=AC,BD 是△ABC 的角分线.若在边 AB 上 截取 BE=BC,连接 DE,则图中等腰三角形共有( ) A. 2 个 B. 3 个 C. 4 个 D. 5 个 第 6 题图 MD AM 8 3 3 2 5 3 5 4 E D CB A BEADABC ,中,∆ =∆∆ ABCEDC SS : ABCD AC BD O OE AB⊥ E =130ADC∠ ° AOE∠ (第 7 题图) (第 9 题图) O DB C A N M D B C A E D CB A 第 9 题图 (15)9. jsc在ABCD 中,AB=10,BC=14,E、F 分别为边 BC、AD 上的点.若四边形 AECF 为正方形,则 AE 的长为( ) A. 7 B. 4 或 10 C. 5 或 9 D. 6 或 8 10、二次函数的考察(标志性的题——无理数 必考) (06)8.如图,抛物线的函数表达式是 【 D 】 A. B. C. D. (07)8.抛物线 的顶点坐标是( ) A. B. C . D. (08)10、已知二次函数 (其中 a>0,b>0,c<0), 关于这个二次函数的图象有如下说法: ①图象的开口一定向上;②图象的顶点一定在第四象限; ③图象与 x 轴的交点至少有一个在 y 轴的右侧。 以上说法正确的个数为( ) A.0 B.1 C.2 D.3 (09)10.根据下表中的二次函数 的自变量 与函数 的对应值,可判断该二 次函数的图象与 轴( ). … … … … A.只有一个交点 B.有两个交点,且它们分别在 轴两侧 C.有两个交点,且它们均在 轴同侧 D.无交点 (10) 10.将抛物线 C:y=x²+3x-10,将抛物线 C 平移到 Cˋ。若两条抛物线 C,Cˋ关于直线 x=1 对称,则下列平移方法中正确的是 (C) A 将抛物线 C 向右平移 个单位 B 将抛物线 C 向右平移 3 个单位 C 将抛物线 C 向右平移 5 个单位 D 将抛物线 C 向右平移 6 个单位 (11)10、若二次函数 y=x2﹣6x+c 的图象过 A(﹣1,y1),B(2,y2),C( , y3),则 y1,y2,y3 的大小关系是( ) A、y1>y2>y3 B、y1>y3>y2 C、y2>y1>y3 D、y3>y1>y2 5 2 22 +−= xxy 22 +−−= xxy 22 ++= xxy 22 ++−= xxy 2 4 7y x x= − − (2 11)−, ( 2 7)− , (211), (2 3)−, 2y ax bx c= + + 2y ax bx c= + + x y x x 1− 0 1 2 y 1− 7 4 − 2− 7 4 − y y (12)10.在平面直角坐标系中,将抛物线 向上(下)或向左(右)平移了 个单位,使平移后的抛物线恰好经过原点,则 的最小值为( ) A.1 B.2 C.3 D.6 (13)10.已知两点 A(-5, )、B(3, )均在抛物线 上, 点 C( , )是该抛物线的顶点,若 > ≥ ,则 的取值范围是( ) A. >-5 B. >-1 C.-5< <-1 D.-2< <3 (14)10.二次函数 y=ax 2 +bx+c(a≠0)的图象如图所示,则下列结论中正确的是 ( ) A.c> -1 B. b>0 C. 2a+b≠0 D.9a2+c>3b (15)10. jscm下列关于二次函数 y=ax2-2ax+1(a>1)的图象与 x 轴交点的判断,正确的是( ) A. 没有交点 B. 只有一个交点,且它位于 y 轴右侧 C. 有两个交点,且它们均位于 y 轴左侧 D. 有两个交点,且它们均位于 y 轴右侧 二、填空题 11、简单的计算题(标志性的题——无理数 必考) (06)11.不等式 的解集为 。 (09)11. =__________. (10)11. 在 1,-2, ,0, π五个数中最小的数是 (11)11、计算: = .(结果保留根号) (12)11.计算: . (13)11.计算: = . (14)1.4 的算术平方根是( )A.-2 B. 2 C.-1 2 D. 1 2 (15) 11. 将实数 5,π,0,-6 由小到大用“<”连起来,可表示为 2、整式的乘法(核心考察幂的运算——逆运算为分解因式) 1y 2y ( )02 ≠++= acbxaxy 0x 0y 1y 2y 0y 0x 0x 0x 0x 0x ( ) ( )03 132 −+− 62 −−= xxy m m )1(32 +≤− xx 2 5−≥x 03 ( 2 1)− − − - 3 ( )0 2cos45 -3 8+ 1- 2 =° y x4-2 -1 第 10 题图 (07)11.计算: . (08)12、计算: · = 。 (10) 3. 计算(-2a²)·3a 的结果是 ( ) A -6a² B-6a³ C12a³ D6a ³ (12)3.计算 的结果是( ) A. B. C. D. (11)13、分解因式:ab2﹣4ab+4a= a(b﹣2)2. (12)12.分解因式: . (13)12.一元二次方程 的根是 . (14)12.因式分解:m(x-y)+n(x-y)= . (15)3.下列计算正确的是( ) A. a2·a3=a6 B. (-2ab)2=4a2b2 C. (a2)3=a5 D. 3a3b2÷a2b2=3ab 12、考察计算器以及有效数字; (06)12.选做题(要求在(1)、(2)中任选一题作答)。 (1)2005 年 11 月 1 日零时,全国总人口为 130628 万人,60 岁及以上的人口占总人口的 11.03%,则全国 60 岁及以上的人口用科学记数法表示约为 万人(用计算器 计算,保留 3 个有效数字)。 (2)用计算器比较大小: 0(填 ) (07) 14.选作题(要求在(1)、(2)中任选一题作答) (1)用计算器计算: (结果保留三个有效数字). (2)小明在楼顶点 处测得对面大楼楼顶点 处的 仰角为 ,楼底点 处的俯角为 .若两座楼 与 相距 60 米,则楼 的高度约为 米. (结果保留三个有效数字). ( ) (12)13.请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分. A.在平面内,将长度为 4 的线段 绕它的中点 ,按逆时针方向旋转 30°,则线段 扫过的面积为 . B.用科学计算器计算: (精确到 0.01). 032 =− xx 2 21( 3 ) 3x y xy − = 2 32a( ) 4a 23 )5( a− 510a− 610a 525a− 625a 3 2 2 3-2 + =x y x y xy 41044.1 × 6173 − ””、“”、““ = 3sin38 2− ≈ A C 52 D 13 AB CD CD sin13 0.2250 cos13 0.9744 tan13 0.2309 sin52 0.7880 cos52 0.6157≈ ≈ ≈ ≈ ≈ , , , , tan52 1.2799≈ AB M AB 7 sin 69° ≈ A B D C 60 米 52 13 ( 第 14 题 图) (13)13.请从经以下两个小题中任选一个作答,若多选,则按所选的第一题计分. A.在平面直角坐标系中,线段 AB 的两个端点的坐标分别为 A(-2,1)、B(1,3,)将线 段 AB 经过平移后得到线段 A′B′.若点 A 的对应点为 A′(3,2),则点 B 的对应点 B′ 的坐标是 . B.比较 8cos31° .(填“>”、“=”若“<”) (14)13.请从以下两个小题中任选一个作答,若多选,则按所选做的第一题计分. A.一个正五边形的对称轴共有 条. B.用科学计算器计算 .(结果精确到 0.01) (15)12.请从以下小题中任选一个作答,若多选,则按第一题计分. A.正八边形一个内角的度数为 B.如图,有一滑梯 AB,其水平宽度 AC 为 5.3 米,铅直高度 BC 为 2.8 米,则∠A 的度 数约为 (用科学计算器计算,结果精确到 0.1°) 第 12 题 B 图 13、反比例函数的考察 (06)15.双曲线 与直线 的交点坐标为 (2,4),( , ) 。 (07)12.在 的三个顶点 中,可能在反比例函数 的图象上的点是 . (08)13、一个反比例函数的图象经过点 P(-1,5),则这个函数的表达式是 。 (09)13 . 若 是 双 曲 线 上 的 两 点 , 且 , 则 {填“>”、“=”、“<”}. (10) 15. 已知 A(x1,y2),B(x2,y2)都在 图像上。若 x1 x2=-3 则 y1y2 的值为 ( 11 ) 8 、 如 图 , 过 y 轴 上 任 意 一 点 P , 作 x 轴 的 平 行 线 , 分 别 与 反 比 例 函 数 的图象交于 A 点和 B 点,若 C 为 x 轴上任意一点,连接 AC,BC, 则△ABC 的面积为( ) 35 C B A 31 3tan56+ ° ≈ xy 8= xy 2= 2− 4− ABC△ (2 3) ( 4 5) ( 3 2)A B C− − − −, , , , , ( 0)ky kx = > 1 1 2 2( ) ( )A x y B x y, , , 3y x = 1 2 0x x> > 1 2_______y y 6y x = A B CD (第 14 题图)(第 14 题图) y xO A D C(B)CDB E A (第 13 题图) A、3 B、4 C、5 D、6 (12)15.在同一平面直角坐标系中,若一个反比例函数的图象与一次函数 的图象 无公共点,则这个反比例函数的表达式是 (只写出符合条件的一个即可). (13)15.如果一个正比例函数的图象与反比例函数 的图象交于 A( , )、B( , )两点,那么( - )( - )的值为 . (14)15.已知 P 1(x1,y1),P 2(x2,y2)是同一个反比例函数图象上的两点,若 x2=x1+2,且 ,则这个反比例函数的表达式为 . (15)13. 如图,在平面直角坐标系中,过点 M(-3,2)分别作 x 轴、y 轴的垂线与反比例函 数 y=4 x的图象交于 A、B 两点,则四边形 MAOB 的面积为 第 13 题图 14、三角形或四边形为载体的几何证明题 (06)13.在同一时刻,小明测得一棵树的影长为 1.6 米的小华影长的 4.5 倍,则这棵树的高 度为 7.2 米。 (07)13.如图, 垂直平分线段 于点 的平分线 交 于点 ,连结 ,则 的度数是 . (08)14、如图,菱形 ABCD 的边长为 2,∠ABC=45°,则点 D 的坐标为 。 (09)14 . 如 图 , 在 梯 形 中 , , . 若 , ,则这个梯形的面积是__________. xy 6= 1x 1y 2x 2y 2x 1x 2y 1y y xO M B A =-2 +6y x 2 1 1 1 1 2y y = + 50ABC AD∠ = , BC D ABC∠, BE AD E EC AEC∠ ABCD DC AB∥ DA CB= 10 4AB DC= =, tan 2A = (10) 13、如图在△ABC 中 D 是 AB 边上一点,连接 CD,要使△ADC 与△ABC 相似,应添 加的条件是 ∠ACD=∠B ∠ADC=∠AOB (13)14.如图,四边形 ABCD 的对角线 AC、BD 相交于点 O,且 BD 平分 AC.若 BD=8,AC=6,∠ BOC=120°,则四边形 ABCD 的面积为 .(结果保留根号) 14.(2014 陕西省,14,3 分)如图,在正方形 ABCD 中,AD=1,将△ABD 绕点 B 顺时针 旋转 45°得到△A′BD′,此时 A′D′与 CD 交于点 E,则 DE 的长度为 . 15、探索规律题(近 5 年已没有考察) (06)14.观察下面图形,按规律在两个箭头所指的“田”字格内分别画上适当图形(只对一 个 2 分) (07)15.小说《达 芬奇密码》中的一个故事里出现了一串神密排列的数,将这串令人费解 的数按从小到大的顺序排列为: ,则这列数的第 8 个数是 . (08)15、搭建如图①的单顶帐篷需要 17 根钢管,这样的帐篷按图②、图③的方式串起来搭 建,则串 7 顶这样的帐篷需要 根钢管。 14、(2011•陕西)一商场对某款羊毛衫进行换季打折销售,若这款羊毛衫每件原价的 8 折 (即按照原价的 80%)销售,售价为 120 元,则这款羊毛衫的原销售价为 150 元 . 15、(2011•陕西)若一次函数 y=(2m﹣1)x+3﹣2m 的图象经过 一、二、四象限,则 m 的 取值范围是 . AD AC AC AB = 11 2 3 5 8,,,,,,… 图① 图② 图③ (第 15 题图) O D B C A (12)14.小宏准备用 50 元钱买甲、乙两种饮料共 10 瓶.已知甲饮料每瓶 7 元,乙饮料每瓶 4 元,则小宏最多能买 瓶甲饮料. 16、填空题中的压轴题(分类思想、几何求最 值、化归思想的考察) (06)16.将一个无盖正方形纸盒展开(如图 ①),沿虚线剪开,用得到的 5 张纸片(其中 4 张是全等的直角三角形纸片)拼成一个正方形 (如图②),则所剪得得直角三角形较短得与较 长得直角边的比是 1∶2 。 (07)16.如图,要使输出值 大于 100,则输入 的最小正整数 是 . (08)16、如图,梯形 ABCD 中,AB∥DC,∠ADC+∠BCD=90° 且 DC=2AB,分别以 DA、AB、BC 为边向梯形外作 正方形,其面积分别为 、 、 ,则 、 、 之间 的关系是 。 ( 陕 西 2009)16 .如 图 ,在 锐 角 中 , , 的 平 分 线 交 于 点 分 别 是 和 上 的 动 点 ,则 的最小值是___________ . (10) 16. 如图,在梯形 ABCD 中,DC∥AB,∠A+∠B=90°若 AB=10,AD=4,DC=5, 则 梯形 ABCD 的面积为 y x 1S 2S 3S 1S 2S 3S ABC△ 4 2 45AB BAC= ∠ =, ° BAC∠ BC D M N, 、 AD AB BM MN+ 输入正整数 x 输出 y ? 偶数奇数 5× 4× 13+ (第 16 题图) 1S 2S 3S (第 16 题图) A B D C A B C D N M ( 第 16 题 图) (11)16、如图,在梯形 ABCD 中,AD∥BC,对角线 AC⊥BD,若 AD=3,BC=7,则梯形 ABCD 面积的最大值 25 . (12)16.如图,从点 发出的一束光,经 轴反射,过点 ,则这束光从点 到 点 所经过路径的长为 . (13)16.如图,AB 是⊙O 的一条弦,点 C 是⊙O 上一动点,且∠ACB=30°,点 E、F 分别是 AC、BC 的中点,直线 EF 与⊙O 交于 G、H 两点.若⊙O 的半径为 7,则 GE+FH 的最大值 为 . (14)16.如图,⊙O 的半径是 2,直线 l 与⊙O 相交于 A、B 两点,M、N 是⊙O 上的两 个 动 点 , 且 在 直 线 l 的 异 侧 , 若 ∠AMB=45° , 则 四 边 形 MANB 面 积 的 最 大 值 是 . (15)14.如图,AB 是⊙O 的弦,AB=6,点 C 是⊙O 上的一个动点,且∠ACB=45°.若 点 M、N 分别是 AB、BC 的中点,则 MN 长的最大值是 ( )0 2A , x ( )4 3B , A B HG F O E B C A (第 16 题图) N M O BA l 第 10 题图 第 14 题图 三、解答题 17、计算题 (06)17.(本题满分 5 分) 解分式方程: (07)17.(本题满分 5 分) 设 ,当 为何值时, 与 的值相等? (08)17、(本题满分 6 分) 先化简,再求值: ,其中 a=-2,b= (09)17.(本题满分 5 分) 解方程: . (10) 17. 化简 (11)17、解分式方程: . (12)17.(本题满分 5 分) 化简: . (13)17.(本题满分 5 分) 解分式方程: . (14)17.先化简,再求值: ,其中 x= - 1 2. N M O C B A 124 2 2 =−+ − x x x 22 3 2 2 =−−+ xx x 2 3 11 1 xA Bx x = = +− −, x A B 2 2 2 a+2b 2b a b a b ++ - 1 3 2 2 312 4 x x x − − =+ − 2 2 2m n mn m n m n m n − +− + − 2 2a b b a b a b a b a b − − ÷ + − + - 2 2 2 1 1 x x x x −− + A B C D E F (第 18 题图) (15)15.计算: 3×(- 6)+|-2 2|+(1 2)-3 (15)16.解分式方程:x-2 x+3- 3 x-3=1 17、三角形和四边形的简单证明 (06)20.(本题满分 8 分) 如图。O 为 的对角线 AC 的中点,过点 O 左一条直线分 别与 AB、CD 交于点 M、N,E、F 在直线 MN 上,且 (07)19.(本题满分 7 分) 如图,在梯形 中, , 延长 到点 ,使 ,连接 . (1)求证: ; (2)若 ,求四边形 的面积. (08)18、(本题满分 6 分) 已知:如图,B、C、E 三点在同一条直线上,AC∥DE, AC=CE,∠ACD=∠B 求证:△ABC≌△CDE (09)18.(本题满分 6 分) 如图,在 中,点 是 的中点, 连接 并延长,交 的延长线于点 F. 求证: . (10) 18. 如图,A、B、C 三点在同一条直线上 AB=2BC,分别以 AB,BC 为边做正方形 ABEF 和正方形 BCMN 连接 FN,EC.求证:FN=EC 【分析】要证 FN=EC,只要证△FEN≌△EBC; OFOE = ABCD 45AB DC DA AB B∠ = ∥ , ⊥ , CD E DE DA= AE AE BC∥ 3 1AB CD= =, ABCE ABCD E AD CE BA FA AB= (第 18 题图) B C E A D E D C BA (第 19 题图) 1 (11)18、在正方形 ABCD 中,点 G 是 BC 上任意一点,连接 AG,过 B,D 两点分别作 BE⊥AG,DF⊥AG,垂足分别为 E,F 两点,求证:△ADF≌△BAE. (12)18.(本题满分 6 分) 如图,在 中, 的平分线 分别与 、 交于点 、 . (1)求证: ; (2)当 时,求 的值. (13)18.(本题满分 6 分) 如图,∠AOB=90°,OA=OB,直线 L 经过点 O,分别过 A、B 两点作 AC⊥L 交 L 于点 C,BD⊥ L 交 L 于点 D. 求证:AC=OD (14)18.如图,在 Rt△ABC 中,∠ABC=90°,点 D 在边 AB 上,使 DB=BC,过点 D 作 EF⊥AC,分别交 AC 于点 E、CB 的延长线于点 F. ABCD ABC∠ BF AC AD E F AB AF= 3 5AB BC= =, AE AC l O D B CA (第 18 题图) 求证:AB=BF 【答案】证明:∵EF⊥AC, ∴∠F+∠C=90°. ∵∠A+∠C=90°, ∴∠A=∠F. 又∵DB=DC,∠FBD=∠ABC, ∴△FBD≌△ABC, ∴AB=BF. (15)19.如图,在△ABC 中,AB=AC,作 AD⊥AB 交 BC 的延长线于点 D,作 AE//BD、 CE⊥AC,且 AE、CE 相交于点 E.求证:AD=CE 第 19 题图 19、三种统计图的考察 (06)19.(本题满分 7 分) 2003~2005 年陕西省财政收入情况如图所示,根据图中的信息,解答下列问题: (1)陕西省这三年财政收入共为多少亿元? (2)陕西省 2004~2005 年财政收入的年增长率约为多少?(精确到 1%) (3)如果陕西省 2005~2006 年财政收入的年增长率与(2)中求得的年增长率基本相同。 请估计陕西省 2006 年财政收入约为多少亿元?(精确到 1 亿元) (07)20.(本题满分 8 分) 2006 年,全国 30 个省区市在我省有投资项 目,投资金额如下表: 省区市 广东 福建 北京 浙江 其它 金额(亿元) 124 67 66 47 119 根据表格中的信息解答下列问题: (1)求 2006 年外省区市在陕投资总额;(2)补全图①中的条形统计图; (3)2006 年,外省区投资中有 81 亿元用于西安高新技术产业开发区,54 亿元用于西安经 济技术开发区,剩余资金用于我省其它地区.请在图②中画出外省区市在我省投资金额使用 E DCB A F E D CB A 第 18 题图 情况的扇形统计图(扇形统计图中的圆心角精确到 ,百分比精确到 1%). (08)19、(本题满分 7 分) 下面图①、图②是某校调查部分学生是否知道母亲生日情况的扇形和条形统计图: 根据上图信息,解答下列问题: (1)求本次被调查学生的人数,并补全条形统计图; (2)若全校共有 2700 名学生,你估计这所学校有多少名学生知道母亲的生日? (3)通过对以上数据的分析,你有何感想?(用一句话回答) (09)19.(本题满分 7 分) 某校为了组织一项球类对抗赛,在本校随机调查了若干名学生,对他们每人最喜欢的一项球 类运动进行了统计,并绘制成如图①、②所示的条形和扇形统计图. 1 120°40° 记不清不知道 知道 图① 知 道 记 不 清 不 知 道 选项 10 30 50 学生数/名 图② 20 40 图 ① 省区 市 图② 2006 年外省区市 在陕投资金额使用情况统计图 (第 20 题图) 0 20 40 60 80 100 120 140 广 东 福 建 北 京 浙 江 其 它 金额/亿元 124 67 66 119 2006 年外省区市在陕投资金额统计图 0 5 10 15 20 10 16 13 学生人数 篮球 足球 乒乓球 羽毛球 其他 项目 ① 足球 20% 篮球 26% 乒乓球 32% 羽毛球 16% 其 他 ② (第 19 题图) 根据统计图中的信息,解答下列问题: (1)求本次被调查的学生人数,并补全条形统计图; (2)若全校有 1 500 名学生,请你估计该校最喜欢篮球运动的学生人数; (3)根据调查结果,请你为学校即将组织的一项球类对抗赛提出一条合理化建议. (10) 19. 某县为了了解“五一”期间该县常住居民出游情况,有关部门随即调查了 1600 名 常住居民,并根据调查结果绘制了如下统计图 根据以上信息,解答下列各题: (1) 补全条形信息统计图。在扇形统计图中,直接填入出游的主要目的是采集发展信息 人数的百分数; (2) 若该县常住居民 24 万人,请估计出游人数; (11)19、某校有三个年级,各年级的人数分别为七年级 600 人,八年级 5 40 人,九年级 565 人,学校为了解学生生活习惯是否符合低碳观念,在全校进行了一次问卷调查,若学生生活 习惯符合低碳观念,则称其为“低碳族”;否则称其为“非低碳族”,经过统计,将全校的低碳 族人数按照年级绘制成如下两幅统计图: (1)根据图①、图②,计算八年级“低碳族”人数,并补全上面两个统计图; (2)小丽依据图①、图②提供的信息通过计算认为,与其他两个年级相比,九年级的“低 碳族”人数在本年级全体学生中所占的比例较大,你认为小丽的判断正确吗?说明 理由. (12)19.(本题满分 7 分) 某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本 校学生从图书馆借出各类图书的数量进行了统计,结果如下图. 请你根据统计图中的信息,解答下列问题: (1)补全条形统计图和扇形统计图; (2)该校学生最喜欢借阅哪类图书? (3)该校计划购买新书共 600 本,若按扇形统计图中的百分比来相应地确定漫画、科普、 文学、其它这四类图书的购买量,求应购买这四类图书各多少本? (13)19.(本题满分 7 分) 我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育的通知》通知中要求各学校 全面持续开展“光盘行动”. 某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了 解很多”,B—“了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了 抽样调查.我们将这次调查的结果绘制了以下两幅统计图. 根据以上信息,解答下列问题: (1) 本次抽样调查了多少名学生? (2) 补全两幅统计图; (3) 若该中学共有 1800 名学生,请你估计这所中学的所有学生中,对“节约教育”内容 “了解较多”的有多少名? (14).19. 根据《2013 年陕西省国民经济和社会发展统计公报》提供的大气污染物(A—二氧化 硫,B—氮氧化物,C—化学需氧量,D—氨氮)排放量的相关数据,我们将这些数据用条 形统计图和扇形统计图统计如下: 根据以上统计图提供的信息,解答下列问题: (1)补全上面的条形统计图和扇形统计图; (2)国务院总理李克强在十二届全国人大二次会议的政府工作报告中强调,建设美好 家园、加大节能减排力度,今年二氧化硫、化学需氧量的排放量在去年基础上要减少 2%, 按此指示精神,求出陕西省 2014 年二氧化硫、化学需氧量的排放量共需减少约多少万吨? (结果精确到 0.1) 陕西省 2013 年大气污染物排放量情况统计图 (15)18.jsc某校为了了解本校九年级女生体育测试项目“仰卧起坐”的训练情况,让体育教 师随机抽查了该年级若干名女生,并严格地对她们进行了 1 分钟“仰卧起坐”测试,同 时统计了每 45% 30% DB C A 了解程度 人数 6 24 0 60 50 40 30 20 10 36 DB CA (第 19 题图) 被调查学生对“节约教育”内容了解程度的统计图 D C 24.2% B A 37.6% 75.9 80.6 0 DCBA 污染物 排放量 (万吨) 80 60 40 20 个人做的个数(假设这个个数为 x),现在我们将这些同学的测试结果分为四个等级:优秀 (x≥44)、良好(36≤x≤43)、及格(25≤x≤35)和不及格(x≤24),并将统计结果绘制 成如下两幅不完整的统计图. 请你根据以上信息,解答下列问题: (1) 补全上面的条形统计图和扇形统计图; (2) 被测试女生 1 分钟“仰卧起坐”个数的中位数落在 等级; (3) 若该年级有 650 名女生,请你估计该年级女生中 1 分钟“仰卧起坐”个数达到优秀的 人数. 被测试女生 1 分钟“仰卧起坐”测试结果统计图 20、测量和计算的考察 (06)18.(本题满分 6 分) 观察下面网格中的图形,解答下列问题: (1)将网格中左图沿水平方向向右平移,使点 A 移至点 处,作出平移后的图形: (2)(1)中作出的图形与右边原有的图形,组成一个新的图形,这个新图形是中心对称图 形,还是轴对称图形? (07)18.(本题满分 6 分) 如图,横、纵相邻格点间的距离均为 1 个单位. (1)在格点中画出图形 先向右平移 6 个单位,再向上平移 2 个单位后的图形; (2)请写出平移前后两图形应对点之间的距离. 13 12 5 0 不及格及格良好优秀 等级 人数 25 20 15 10 5 40% 26% 10% 不及格 及格 良好 优秀 A′ ABCD A D B C (第 18 题图) (第 20 题图) (08)20、(本题满分 7 分) 阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达, 顶部不易到达),他们带了以下测量工具:皮尺、标杆、一副三角尺、小平面镜。请你在他 们提供的测量工具中选出所需工具,设计一种测量方案。 (1)所需的测量工具是: ; (2)请在下图中画出测量示意图; (3)设树高 AB 的长度为 x,请用所测数据(用小写字母表示)求出 x. (09)20.(本题满分 8 分) 小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针 对这种情况,他设计了一种测量方案,具体测量情况如下: 如示意图,小明边移动边观察,发现站到点 处时,可以使自己落在墙上的影子与这栋楼 落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度 m, m, m(点 在同一直线上). 已知小明的身高 是 1.7m,请你帮小明求出楼高 (结果精确到 0.1m). (10) 20. 再一次测量活动中,同学们要测量某公园的码头 A 与他正东方向的亭子 B 之间的 距离,如图他们选择了与码头 A、亭子 B 在同一水平面上的点 P 在点 P 处测得码头 A 位于 点 P 北偏西方向 30°方向,亭子 B 位于点 P 北偏东 43°方向;又测得 P 与码头 A 之间的 距离为 200 米,请你运用以上数据求出 A 与 B 的距离. E 1.2CD = 0.8CE = 30CA = A E C、 、 EF AB A B C D F E (第 20 题图) (11)20、一天,数学课外活动小组的同学们,带着皮尺去测量某河道因挖沙形成的“圆锥 形坑”的深度,来评估这些坑道 对河道的影响,如图是同学们选择(确保测量过程中无安全 隐患)的测量对象,测量方案如下: ①先测出沙坑坑沿的圆周长 34.54 米; ②甲同学直立于沙坑坑沿的圆周所在的平面上,经过适当调整自己所处的位置,当他位于 B 时恰好他的视线经过沙坑坑沿圆周上一点 A 看到坑底 S(甲同学的视线起点 C 与点 A,点 S 三点共线),经测量:AB=1.2 米,BC=1.6 米. 根据以上测量数据,求圆锥形坑的深度(圆锥的高).(π 取 3.14,结果精确到 0.1 米) (12)20.(本题满分 8 分) 如图,小明想用所学的知识来测量湖心岛上的迎宾槐与岸上的凉亭间的距离,他先在湖岸上 的凉亭 处测得湖心岛上的迎宾槐 处位于北偏东 方向,然后,他从凉亭 处沿湖岸 向正东方向走了 100 米到 处,测得湖心岛上的迎宾槐 处位于北偏东 方向(点 在同一水平面上).请你利用小明测得的相关数据,求湖心岛上的迎宾槐 处与 湖岸上的凉亭 处之间的距离(结果精确到 1 米). (参考数据: , ) A C 65° A B C 45° A B C、 、 C A sin 25 0.4226 cos25 0.9063 tan 25 0.4663 sin 65 0.9063° ≈ ° ≈ ° ≈ ° ≈, , , cos65 0.4226 tan 65 2.1445° ≈ ° ≈, (13) 20.(本题满分 8 分) 一天晚上,李明和张龙利用灯光下的影子长来测量一路灯 D 的高度.如图,当李明走到点 A 处时,张龙测得李明直立向高 AM 与其影子长 AE 正好相等;接着李明沿 AC 方向继续向前走, 走到点 B 处时,李明直立时身高 BN 的影子恰好是线段 AB,并测得 AB=1.25m.已知李明直立 时的身高为 1.75m,求路灯的高度 CD 的长.(精确到 0.1m) (14)20.某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条和的大致宽度, 两人在确保无安全隐患的情况下,先在河岸边选择了一点 B(点 B 与河对岸岸边上的一 棵树的底部点 D 所确定的直线垂直于河岸). ①小明在 B 点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点 D 处,如图所示,这时小亮测得小明眼睛距离地面的距离 AB=1.7 米;②小明站在原地转动 180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通 过帽檐落在了 DB 延长线上的点 E 处,此时小亮测得 BE=9.6 米,小明的眼睛距地面的距 离 CB=1.2 米. 根据以上测量过程及测量数据,请你求出河宽 BD 是多少米? 【答案】 解:由题意,知∠BAD=∠BCE. ∵∠ABD=∠ABD=90°, ∴△BAD∽△BCD. ∴BD BE =AB CB. ∴BD 9.6 = 1.7 1.2. ∴BD=13.6. ∴河流的宽 BD 是 13.6 米. NM E D B CA (第 20 题图) D E C B A (15)20.晚饭后,小聪和小军在社区广场散步,小聪问小军:“你有多高?”小军一时语 塞,小聪思考片刻,提议用广场照明灯下的影长及地砖长来测量小军的身高.于是,两人 在灯下沿着直线 NQ 移动,当小军正好站在广场的 A 点(距 N 点 5 块地砖长)时,其影长 AD 恰好为 1 块地砖长;当小军正好站在 B 点(距 N 点 9 块地砖长)时,其影长 BF 恰好为 2 块地砖长.已知广场第面由边长为 0.8 米的正方形地砖铺成,小聪的身高 AC 为 1.6 米, MN⊥NQ,AC⊥NQ,BE⊥NQ.请你根据以上信息,求出小军身高 BE 的长.(结果精确 到 0.01 米) 第 20 题图 21、一次函数应用题的考察 (06)21.(本题满分 8 分) 甲、乙两车从 A 地出发,沿同一条高速公路行驶至距 A 地 400 千米的 B 地, 分别 表示甲、乙两车行驶路程 (千米)与时间 (时)之间的关系 (如图所示)。根据图像提供的信息,解答下列问题: (1)求 的函数表达式(不要求写出 的取值范围) (2)甲、乙两车哪一辆先到达 B 地?该车比另一辆车早多长 时间到达 B 地? 解:(1)设 的函数表达式是 ,则 (07)21.(本题满分 8 分) 为了迎接暑期旅游,某旅行社推出了一种价格优惠方案:从现在开始,各条旅游线路的价格 每人 (元)是原来价格每人 (元)的一次函数.现知道其中两条旅游线路原来旅游价格 分别为每人 2100 元和 2800 元,而现在旅游的价格分别为每人 1800 元和 2300 元. (1)求 与 的函数关系式(不要求写出 的取值范围); (2)王老师想参加该旅行社原价格为 5600 元的一条线路的 21 ll 、 y x 2l x 2l bxky += 2 y x y x x 暑期旅游,请帮王老师算出这条线路的价格. (08)22、(本题满分 8 分) 生态公园计划在园内的坡地上造一片有 A、B 两种树的混合林,需要购买这两种树苗 2000 棵。种植 A、B 两种树苗的相关信息如下表: 设购买 A 种树苗 x 棵,造这片林的总费用为 y 元。解答下列问题: (1)写出 y(元)与 x(棵)之间的函数关系式; (2)假设这批树苗种植后成活 1960 棵,则造这片林的总费用需多少元? (09)21.(本题满分 8 分) 在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从 甲地出发 (h)时,汽车与甲地的距离为 (km), 与 的函数关系如图所示. 根据图象信息,解答下列问题: (1)这辆汽车的往、返速度是否相同?请说明理由; (2)求返程中 与 之间的函数表达式; (3)求这辆汽车从甲地出发 4h 时与甲地的距离. (10) 21. 某蒜薹生产基地喜获丰收收蒜薹 200 吨。经市场调查,可采用批发、零售、冷库 x y y x y x 品种 项目 单价(元/棵) 成活率 劳务费(元/棵) A 15 95% 3 B 20 99% 4 2 2.5 5 (第 21 题图) 120 O y/km x/h 储藏后销售,并按这三种方式销售,计划每吨的售价及成本如下表: 销售方式 批发 零售 冷库储藏后销售 售价(元/吨) 3000 4500 5500 成本(元/吨) 700 1000 1200 若经过一段时间,蒜薹按计划全部售出后获得利润为 y(元)蒜薹 x(吨),且零售是批发 量的 . (1)求 y 与 x 之间的函数关系; (2)由于受条件限制经冷库储藏的蒜薹最多 80 吨,求该生产基地计划全部售完蒜薹获得最大 利润. (11)21、2011 年 4 月 28 日,以“天人长安,创意自然一一城市与自然和谐共生”为主题的 世界园艺博览会在西安隆重开园,这次园艺会的门票分为个人票和团体票两大类,其中个人 票设置有三种: 票得种类 夜票(A) 平日普通票(B) 指定日普通票(C) 单价(元/张) 60 100 150 某社区居委会为奖励“和谐家庭”,欲购买个人票 100 张,其中 B 种票的张数是 A 种票张数 的 3 倍还多 8 张,设购买 A 种票张数为 x,C 种票张数为 y (1)写出 y 与 x 之间的函数关系式; (2)设购票总费用为 W 元,求出 W(元)与 X(张)之间的函数关系式; (3)若每种票至少购买 1 张,其中购买 A 种票不少于 20 张,则有几种购票方案?并求出 购票总费用最少时,购买 A,B,C 三种票的张数. (12)21.(本题满分 8 分) 科学研究发现,空气含氧量 (克/立方米)与海拔高度 (米)之间近似地满足一次函数 关系.经测量,在海拔高度为 0 米的地方,空气含氧量约为 299 克/立方米;在海拔高度为 2000 米的地方,空气含氧量约为 235 克/立方米. (1)求出 与 的函数表达式; (2)已知某山的海拔高度为 1200 米,请你求出该山山顶处的空气含氧量约为多少? (13)21.(本题满分 8 分) “五一节”期间,申老师一家自架游去了离家 170 千米的某地.下面是他们离家的距离 (千米)与汽车行驶时间 (小时)之间的函数图象. (1) 求他们出发半小时时,离家多少千米? (2) 求出 AB 段图象的函数表达式; (3) 他们出发 2 小时时,离目的地还有多少千米? y x 3 1 y x y x x/小时 y/千米 2.51.5 170 90 O B A (14)21.小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这 个公司除了收取每次 6 元包装费外,樱桃不超过 1kg 收费 22 元,超过 1kg,则超出部分每 千克 10 元加收费用,设该公司从西安到南昌快寄樱桃的费用为 y(元),所寄樱桃为 x(kg) (1)求 y 与 x 之间的函数关系式; (2)已知小李给外婆快寄了 2.5kg 樱桃,请你求出这次快寄的费用是多少元? 【答案】 解:(1)当 0查看更多