南宁市2013年中考数学卷

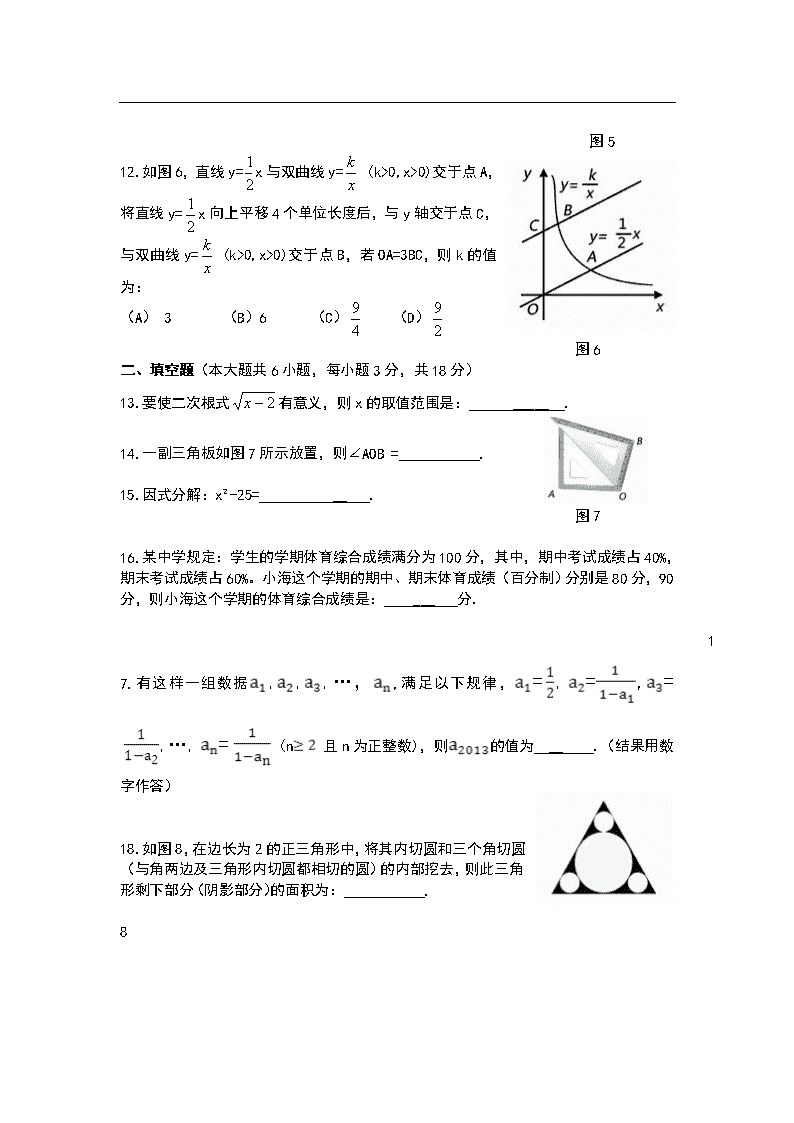
南宁市2013年中考数学卷

‎2013年南宁市初中毕业升学考试数学试卷 满分120分，考试时间120分钟 一、选择题（本大题共12小题，每小题3分，共36分）‎ 每小题都给出代号为（A）、（B）、（C）、（D）四个结论，其中只有一个是正确的。‎ ‎1.在-2，1，5，0这四个数中，最大的数是：‎ ‎（A）-2 （B）1 （C）5 （D）0‎ ‎2.如图1所示，将平面图形绕轴旋转一周，得到的几何体是：‎ ‎（A） （B） 图1 （C） （D）‎ ‎3.‎2013年6月11日，神舟十号飞船发射成功，神舟十号飞船身高约‎9米，重约8吨，飞行速度约每秒‎7900米，将数7900用科学记数法表示，正确的是：‎ ‎（A）0.79× （B）7.9× （C）7.9× （D）79×‎ ‎4.小乐用一块长方形硬纸板在阳光下做投影实验，通过观察，发现这块长方形硬纸板在平整的地面上不可能出现的投影是：‎ ‎（A）三角形 （B）线段 （C）矩形 （D）正方形 ‎5.甲、乙、丙、丁四名选手参加‎100米决赛，赛场共设1、2、3、4四个跑道，选手以随机抽签的方式决定各自的跑道，若甲首先抽签，则甲抽到1号的概率是：‎ ‎（A）1 （B） （C） （D）‎ ‎6.若分式的值为0，则x的值为：‎ ‎（A）-1 （B）0 （C）2 （D）-1或2 ‎ ‎7.如图2，圆锥形的烟囱帽底面半径为15cm，母线长为20cm，制作这样一个烟囱帽所需要的铁皮面积至少是：‎ ‎ ‎ ‎（A）150πcm² （B）300πcm² （Ｃ）600πcm² （D）150cm²‎ ‎（ 图2‎ ‎ ‎ ‎8.下列各式计算正确的是：‎ ‎ （A）3+2=5 (B)2+=3 (C)= (D)=a ‎9.陈老师打算购买气球装扮学校“六一”儿童节活动会场，起球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同，由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图3所示，则第三束气球的价格为：‎ ‎（A）19 ‎ ‎（B）18 ‎ ‎（C）16 ‎ ‎（D）15 ‎ ‎ 图3‎ ‎10.已知二次函数y=ax²+bx+c（c≠0）的图像如图4所示，下列说法错误的是：‎ ‎（A）图像关于直线x=1对称 ‎（B）函数y=ax²+bx+c（c ≠0）的最小值是 -4‎ ‎（C）-1和3是方程ax²+bx+c=0（c ≠0）的两个根 ‎（D）当x＜1时，y随x的增大而增大 图4‎ ‎11.如图5，AB是O的直径，弦CD交AB于点E，且AE=CD=8，∠BAC =∠BOD，则的半径为：‎ ‎（A）4 （B）5 （C）4 （D）3‎ ‎ ‎ ‎ 图5‎ ‎12.如图6，直线y=x与双曲线y= (k>0,x>0)交于点A，将直线y=x向上平移4个单位长度后，与y轴交于点C，与双曲线y= (k>0,x>0)交于点B，若OA=3BC，则k的值为：‎ ‎（A） 3 （B）6 （C） （D）‎ ‎ 图6‎ 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎13.要使二次根式有意义，则x的取值范围是： _____ .‎ ‎14.一副三角板如图7所示放置，则∠AOB = ___ .‎ ‎15.因式分解：x²-25= __ .‎ ‎ 图7‎ ‎16.某中学规定：学生的学期体育综合成绩满分为100分，其中，期中考试成绩占40%，期末考试成绩占60%。小海这个学期的期中、期末体育成绩（百分制）分别是80分，90分，则小海这个学期的体育综合成绩是： ___ 分.‎ ‎17.有这样一组数据,,,…，,满足以下规律，=,=,=,…,= (n 且n为正整数)，则的值为 __ .（结果用数字作答）‎ ‎18.如图8，在边长为2的正三角形中，将其内切圆和三个角切圆（与角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为： . ‎ 图8‎ ‎ ‎ 第三至第八大题为解答题，要求写出解答过程，如果运算结果含有根号，请保留根号。‎ 三、（本大题共2小题，每小题满分6分，共12分）‎ ‎19、 计算：- + 2cos60°+（-2）‎ ‎20、先化简，再求值：（ +），其中x=-2.‎ 四、（本大题共2小题，每小题满分8分，共16分）‎ ‎21、如图9，ABC三个顶点坐标分别为A（-1,3），B（-1,1），C（-3,2）。‎ ‎（1）请画出ABC关于Y轴对称的 。‎ ‎（2）以原点O为位似中心，将放大为原来的2倍，得到,并求出:的值。‎ ‎ ‎ ‎ ‎ 图 图9‎ ‎22、2013年6月，某中学结合广西中小学生阅读素养评估活动，以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图10-①和10-②所提供的信息，解答下列问题：‎ ‎（1）在这次抽样调查中，一共抽查了多少名学生？‎ ‎（2）请把折线统计图（图10- ‎ ‎①）补充完整；‎ ‎（3）求出扇形统计图（图10- ‎ ‎②）中，体育部分所对应 ‎ 的圆心角的度数。‎ ‎（4）如果这所中学共有学生 ‎ ‎1800名，那么请你估计最喜爱 图10-① 图10-②‎ 科普类书籍的学生人数。 ‎ ‎ ‎ 五、（本大题满分8分）‎ ‎23、如图11，在菱形ABCD中，AC是对角线，点E、F分别是边BC、AD的中点。‎ ‎（1）求证：ABE≌CDF。‎ ‎（2）若∠B=60°，AB=4，求线段AE的长。‎ ‎ 图11‎ 六、（本大题满分10分）‎ ‎24、在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地，乙骑摩托车从B地到A地，到达A地后立即按原路返回，是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象，根据图象解答以下问题：‎ ‎（1）写出A、B两地之间的距离；‎ ‎（2）求出点M的坐标，并解释该点坐标所表示的实际意义；‎ ‎（3）若两人之间的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围。‎ ‎ 图12‎ ‎ ‎ 七、（本大题满分10分）‎ ‎25、如图13，在ABC中，∠BAC=90，AB=AC，AB是O的直径，O交BC于点D，DEAC于点E，BE交O于点F，连接AF的延长线交DE于点P。‎ ‎（1）求证：DE是O的切线。‎ ‎（2）求tan∠ABE的值；‎ ‎（3）若OA=2，求线段AP的长。‎ ‎ ‎ 八、（本大题满分10分）‎ ‎26、如图14，抛物线y=a+c(c0)经过C（2,0）D（0，-1）两点，并与直线y=kx交于A、B两点，直线l过点E（0,-2）且平行于X轴，过A、B两点分别作直线l的垂线，垂足分别为点M、N。‎ ‎（1）求此抛物线的解析式；‎ ‎（2）求证：AO=AM；‎ ‎（3）探究：‎ ‎①当k=0时，直线y=kx与x轴重合，求出此时 的值；‎ ‎②试说明无论k取何值，的值都等于同一个常数。 图14‎ ‎ ‎ ‎2013年南宁市初中毕业升学考试数学试卷答案 选择题+填空题（每小题3分，共54分）‎ 选择 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C A C A D C B B C D B D 填空 ‎13‎ ‎14‎ ‎15‎ ‎16‎ ‎17‎ ‎18‎ X≥2‎ ‎105°‎ ‎（X+5）（X-5）‎ ‎86‎ ‎-1‎ π ‎©海壁教育——致力于让数学更简单，更有效，更有趣！ 咨询电话：400-070-2005‎ ‎【解析】12、过点B作BH⊥y轴，交y轴于H，过点A做AG⊥y轴交y轴于点G，不难证明△BCH∽△AOG，∵OA=3BC，∴AG=3BH。‎ 设BH=a，AG=3a，∴B（a， a+4），A（3a， a）‎ ‎∵B、A两点也在反比例函数的图像上，∴ a+4=3· a ‎∴a=1，∴B（1,）,A（3， ），∴k=‎ ‎ 18、如图，设该等边三角形是ABC及内切大圆圆心为0，半径为R。上角切圆圆心为D，半径为r。过点A做AH⊥BC交BC于点H。‎ RT△AHC中，HC=1，∠HAC=30°，AH=，△ABC面积S=1/2×2×=‎ RT△OHC中，HC=1，∠HCO=30°，HO=R=，内切大圆面积S1=π RT△ADE中，∠DAE=30°，AD=2DE=2r，AH=3r+2R=，求出r=，‎ 小角切圆的面积S2=π。三个的面积为π 所以，阴影部分面积=ππ=π 计算题+图像题+几何题+应用题（19、20题6分，21、22、23题8分）‎ ‎19、-‎ ‎20、解：原式化简得：x-1，最后结果是：-3‎ ‎21、（1）（2）如图所示 ‎: =‎ ‎22、（1）300人 ‎（2）如右图所示 ‎（3）48°‎ ‎（4）480人 ‎23、（1）证明： △ABE和△CDF中，BE=FD，∠B=∠D，AB=CD（过程略）‎ ‎（2） 2‎ ‎24、（1）30km ‎（2）M点坐标为（ , 20）。该坐标表示小时后两车相遇，此时距离B地20km ‎（3）≤x≤和≤x≤2‎ ‎25（10分）、（1）证明：多种方法，如证OD∥AC，DE∥AB ， 则∠ODE=∠DOB=∠CAB=90°，证毕 ‎（2）‎ ‎（3）利用等角代换或相似：AP=‎ ‎26、（10分）（1）y=x²-1‎ ‎（2）证明：延长MA交X轴于点H，同时，设点A横坐标为t（t＜0），则A点坐标为（t，kt）和（t，t²‎ ‎-1），其中kt=t²-1‎ AM=kt-（-2）=kt+2 ；AH=-kt=t² ；OH=-t；‎ OA= ===1+=kt+2=AM ‎（3）①+=1‎ ‎②设A点横坐标为a，B点横坐标为b，经分析a、b分别为方程kt=t²-1的两根，根据韦达定理得，a+b=4k，ab=-4‎ a点坐标是（a，ak），b点 坐标为（b，bk），AM=ak+2，BN=bk+2 ‎ ‎===‎ 将a+b=4k，ab=-4代入，得 ===1‎