2012中考数学模拟试题及答案十

2012中考数学模拟试题及答案十

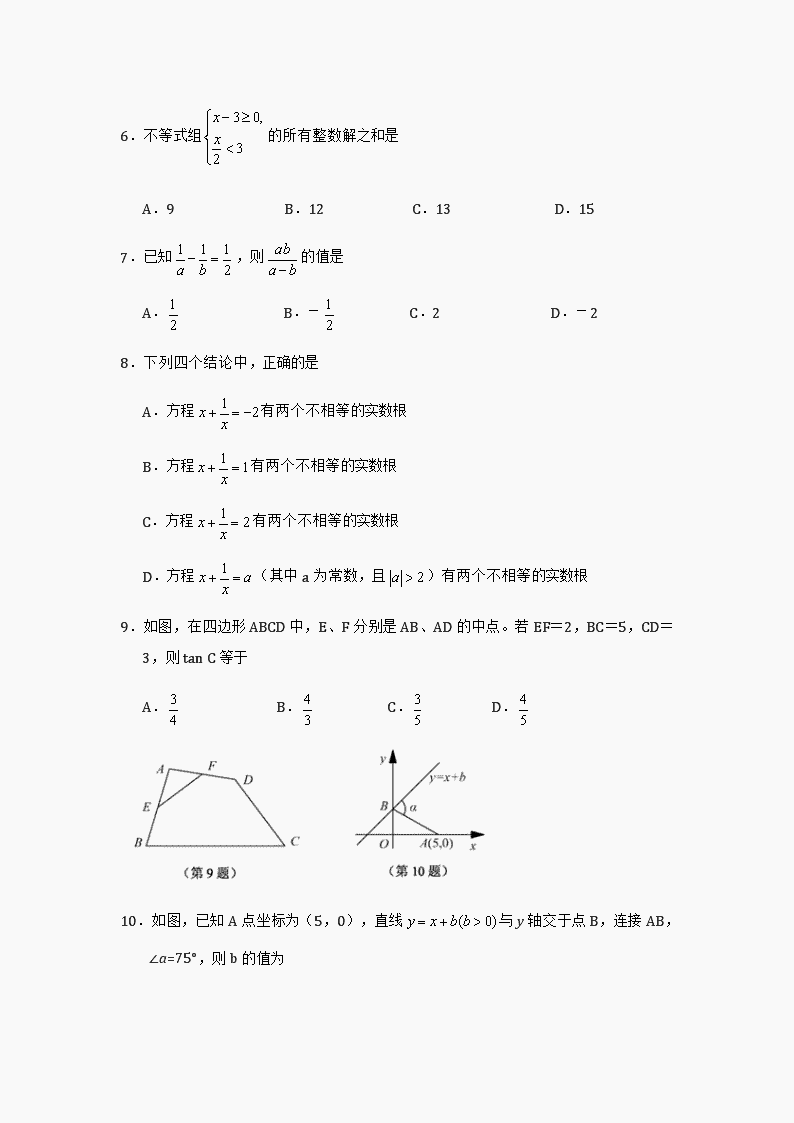
‎2012中考数学模拟试题及答案十 注意事项：‎ ‎1．本卷满分为120分，考试时间为120分钟．‎ ‎2．必须用0．5毫米黑色签字笔或黑色墨水钢笔作答． ‎ ‎3. 请认真审题，相信你一定有出色的表现！！‎ 一、选择题（本大题共12小题，每小题只有唯一正确答案，每小题3分，共36分）‎ ‎1．的结果是 ‎ A．－4 B．－‎1 C． D．‎ ‎2．△ABC的内角和为 ‎ A．180° B．360° C．540° D．720°‎ ‎3．已知地球上海洋面积约为316 000 ‎000km2，316 000 000这个数用科学记数法可表示为 ‎ A．3.61×106 B．3.61×‎107 C．3.61×108 D．3.61×109‎ ‎4．若m·23＝26，则m等于 ‎ A．2 B．‎4 ‎‎ C．6 D．8‎ ‎5．有一组数据：3，4，5，6，6，则下列四个结论中正确的是 ‎ A．这组数据的平均数、众数、中位数分别是4.8，6，6‎ B．这组数据的平均数、众数、中位数分别是5，5，5‎ C．这组数据的平均数、众数、中位数分别是4.8，6，5‎ D．这组数据的平均数、众数、中位数分别是5，6，6‎ ‎6．不等式组的所有整数解之和是 ‎ A．9 B．‎12 ‎‎ C．13 D．15‎ ‎7．已知，则的值是 ‎ A． B．－ C．2 D．－2‎ ‎8．下列四个结论中，正确的是 ‎ A．方程有两个不相等的实数根 B．方程有两个不相等的实数根 C．方程有两个不相等的实数根 D．方程（其中a为常数，且）有两个不相等的实数根 ‎9．如图，在四边形ABCD中，E、F分别是AB、AD的中点。若EF＝2，BC＝5，CD＝3，则tan C等于 ‎ A． B． C． D．‎ ‎10．如图，已知A点坐标为（5，0），直线与y轴交于点B，连接AB，∠a=75°，则b的值为 ‎ A．3 B． C．4 D．‎ 第12题图 ‎11． 某市按以下标准收取水费：用水不超过20吨，按每吨1．2元收费，超过20吨则超过部分按每吨1．5元收费．某家庭五月份的水费是平均每吨1．25元，那么这个家庭五月份应交水费（ ）‎ A．20元 B．24元 C．30元 D．36元 ‎12． 如图，在斜坡的顶部有一铁塔AB，B是CD的中点，CD是水平的，在阳光的照射下，塔影DE留在坡面上．已知铁塔底座宽CD=12 m，塔影长DE=18 m，小明和小华的身高都是1．6m，同一时刻，小明站在点E处，影子在坡面上，小华站在平地上，影子也在平地上，两人的影长分别为2m和1m，那么塔高AB为（ ）‎ A．24m B．22m C．20 m D．18 m 二、填空题（每题3分，共15分）‎ ‎13．计算：(－)(＋)＝ ．‎ ‎14．如图,中,∥∥,且,则 ．‎ ‎15．如图,点是正三角形的中心,分别是的中点,则与是位似三角形,此时与的位似中心是_____,位似比为______．‎ ‎[来源:Z|xx|k.Com]‎ 第15题图 第14题图 第17题图 ‎16．如图，有一张面积为1的正方形纸片ABCD，M、N分别是AD，BC边的中点，将C点折叠至N上，落在P点的位置，折痕为BQ，连结PQ，则PQ=______．‎ ‎17．如图，AB为半圆的直径，C是半圆弧上一点，正方形DEFG的一边DG在直径AB上，另一边DE过ΔABC的内切圆圆心O，且点E在半圆弧上．①若正方形的顶点F也在半圆弧上，则半圆的半径与正方形边长的比是______________；②若正方形DEFG的面积为100，且ΔABC的内切圆半径=4，则半圆的直径AB = __________．‎ 三、简答题（69分）：‎ ‎18．（8分）已知是一元二次方程的实数根，求代数式的值．‎ ‎ 19．(9分) 已知关于x的方程x2－2(m＋1)x＋m2＝0‎ ‎（1）当m取什么值时，原方程没有实数根；‎ ‎（2）对m选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根的平方和．‎ ‎20．(10分) 如图，□ABCD中，点E是CD延长线上一点，BE交与AD于点F，．‎ ‎（1）求证：△ABF∽△CEB；（2）若△DEF的面积为2，求□ABCD的面积；‎ ‎（3）若G、H分别为BF、AB的中点，AG、FH交于点O，求．‎ 第20题图 ‎[来源:学.科.网Z.X.X.K]‎ ‎21．（10分）有A、B两个黑布袋，A布袋中有四个除标号外完全相同的小球，小球上分别标有数字0，1，2，3， B布袋中有三个除标号外完全相同的小球，小球上分别标有数字0，1，2．小明先从A布袋中随机取出—个小球，用m表示取出的球上标有的数字，再从B布袋中随机取出一个小球，用n表示取出的球上标有的数字．‎ ‎ (1)若用(m，n)表示小明取球时m与n 的对应值，请画出树状图并写出(m，n)的所有取值； (2)求关于x的一元二次方程有实数根的概率．‎ ‎22．（10分）已知：如图1，AB⊥BD，CD⊥BD，垂足分别为B、D，AD和BC相交于点E，EF⊥BD，垂足为F，我们可以证明成立（不要求考生证明）．若将图1中的垂线改为斜交，如图2，AB∥CD，AD、BC相交于点E，过点E作EF∥AB，交BD于点F，则：‎ 第22题图1‎ C D F B A E F C D E A B 第22题图2‎ ‎（1）还成立吗？如果成立，请给出证明；‎ 如果不成立，请说明理由；‎ ‎（2）请找出S△ABD，S△BED和S△BDC间的关系式，并给出证明．‎ ‎23． （10分）如图，是以为直径的⊙O上一点，于点，过点作⊙O的切线，与的延长线相交于点是的中点，连结并延长与相交于点，延长与的延长线相交于点．‎ ‎（1）求证：；‎ ‎（2）求证：是⊙O的切线；‎ ‎（3）若，且⊙O的半径长为，求和的长度．‎ O D G C A E F B P 第23题图 ‎24． （12分）在平面直角坐标系中，现将一块等腰直角三角板放在第二象限，斜靠在两坐标轴上，且点，点，如图所示：抛物线经过点．‎ ‎（1）求点的坐标；‎ ‎（2）求抛物线的解析式；‎ ‎（3）在抛物线上是否还存在点（点除外），使仍然是以为直角边的等腰直角三角形？若存在，求所有点的坐标；若不存在，请说明理由．‎ B A C x y ‎（0，2）‎ ‎（－1，0）‎ 第24题图 参考答案 一、选择题 ‎1．A 2.B 3.D 4.B 5.C 6.C ‎ ‎7.A 8.C 9.B 10. B 11. C 12.A ‎ 二、填空题 ‎ 13.1； 14. 4:21:56；15. 点O， ；16． ；17．：①②21‎ 三、解答题 ‎【18题答案】化简为……………3分 由得……………5分 代值得……………8分 ‎【19题答案】解：（1）∵方程没有实数根 ∴b2－4ac=[－a（m+1）]2－4m2=8m+4＜0，……………2分 ‎∴m＜， ‎ ‎∴当m＜时，原方程没有实数根；……………4分 ‎（2）由（1）可知，m≥时，方程有实数根，‎ ‎∴当m=1时，原方程变为x2－4x+1=0，……………6分 设此时方程的两根分别为x1，x2，‎ 则x1+x2=4，x1•x2=1，‎ ‎∴x12+x22=（x1+x2）2－2x1x2=16－2=14，……………8分 ‎∴当m=1时，原方程有两个实数根，这两个实数根的平方和是14．……………9分 ‎【20题答案】（1）证明：∵AB∥CE，∴∠ABF=∠E,‎ 又∵ABCD是平行四边形，∴∠BAF=∠C,‎ ‎△ABF∽△CEB……………3分 ‎（2）∵∠ABF=∠E, ∠AFB=∠E FC 故△ABF∽△DEF 同理△CEB∽△DEF……………4分 ‎,∴‎ 又已知△DEF的面积为2， ‎ 第20题图 ‎∴……………6分 进而有 ‎……………7分 ‎（3）∵G、H为中点，‎ ‎∴GH∥AF且，……………8分[来源:学_科_网]‎ ‎∴有OG:OA=HG:AF＝1：2. ……………10分 ‎【21题答案】解：依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．‎ ‎……………4分 ‎∴（m，n）所有取值是（0，0），（0，1）， （0，2），（1，0），（1，1），（1，2），（2，0），（2，1），（2，2），（3，0），（3，1），（3，2）．共12个；……………5分 ‎△≥0，原方程有实数根．‎ 故P（△≥0）=8/12=2/3．‎ 答：原方程有实数根的概率为2/3 ．……………10分 ‎【22题答案】证明：（1）∵AB∥EF[来源:学科网]‎ ‎∴ EF/AB=DF/DB ‎∵CD∥EF[来源:学科网ZXXK]‎ ‎∴ EF/CD=BF/DB ‎∴ EF/AB+EF/CD=DF/DB+BF/DB= DB/DB=1……………4分 ‎∴ 1/AB+1/CD=1/EF；……………5分 ‎（2）关系式为： 1/S△ABD+1/S△BDC=1/S△BED……………6分 证明如下：分别过A作AM⊥BD于M，过E作EN⊥BD于N，过C作CK⊥BD交BD的延长线于K 由题设可得： 1/AM+1/CK=1/EN ‎∴ 2/BD•AM+2/BD•CK= 2/BD•EN 即 1/1/2•BD•AM+1/1/2•BD•CK……………8分 又∵ 1/2•BD•AM=S△ABD， 1/2•BD•CK=S△BCD ‎∴ 1/2•BD•EN=S△BCD ‎∴ 1/S△ABD+1/S△BDC=1/S△BED．……………10分 ‎【23题答案】（1）∵BE是⊙O得切线，‎ O D G C A E F B P ‎∴BE⊥BC,‎ 又∵AD⊥BC ‎∴AD∥BE ‎∴AG:EF=CG:CF=DG:BF 又∵AG=GD BF=EF……………3分 ‎(2)连接AB．OA ‎∵BC是直径 ‎∴∠BAC=∠BAE=90‎ 又∵BF=EF ‎∴BF=AF ‎∴∠FBA=∠FAB 而OA=OB ‎∴∠OBA=∠OAB ‎∴∠FBO=∠FAO=90‎ 即PA是圆O的切线……………6分 ‎（3）连接BG ‎∵EF=AF=FB=FG BE‖AD ‎∴∠BFG=∠FGA=∠FAG=∠EFA ‎∴△FAE≌△FBG, AC:AE=CD:BD ‎∴AE=BG ‎∴AC:BG=CD:BD 又∵AD⊥BC ‎∴RT△BDG∽RT△CDA ,AD²=BD*DC ‎∴CD:BD=AD:DG=2:1……………8分 ‎∴BD=1/3BC=1/3*2*3√2=2√2, ‎ ‎∴ DC=4√2‎ ‎∴AD=4‎ ‎∴DG=1/2AD=2‎ 又∵BF∥AD ‎∴DG:BF=CD:BC=2:3‎ ‎∴BF=3=FG……………10分 ‎【24题答案】解：（1）过B作BD⊥x轴于D；‎ ‎∵∠BCA=90°， ∴∠BCD=∠CAO=90°－∠ACO； 又∵BC=AC，∠BDC=∠AOC=90°， ∴△BDC≌△COA； ∴AO=DC=2，BD=OC=1， ∴B（－3，1）．……………3分[来源:学|科|网Z|X|X|K]‎ ‎（2）由于抛物线过B点，则有：‎ ‎2a×9+（－3）•a－=1， 解得a=； ∴y=x2+x－．……………7分 ‎（3）①若以AC为直角边，C为直角顶点； 设直线BC交抛物线y=x2+x－于P1， 易求得直线BC的解析式为y=－x－； 不难求得P1（1，－1），此时CP1=AC； ∴△ACP1为等腰直角三角形；……………9分 ②若以AC为直角边，点A为直角顶点； 过A作AF∥BC，交抛物线y=x2+x－于P2，易求得直线AF的解析式为y=－x+2； 不难得出P2（，）或（，）（不合题意舍去）； 此时AP2≠AC， ∴△ACP2不是等腰直角三角形；……………11分 ∴符合条件的P点有一个：P（1，－1）．………‎