2011年贵阳市初中毕业生学业考试试题

2011年贵阳市初中毕业生学业考试试题

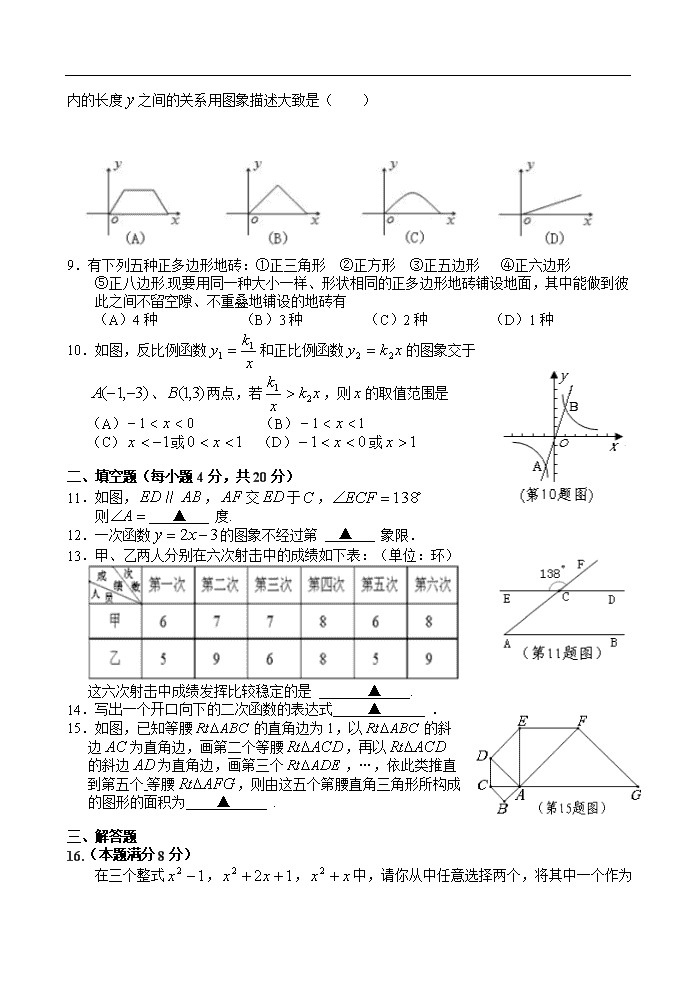
贵阳市2011年初中毕业生学业考试试题卷 数 学 考生注意： ‎ ‎1.本卷为数学试题卷，全卷共4页，三大题25小题，满分150分．考试时间为120分钟．‎ ‎2.一律在《答题卡》相应位置作答，在试题卷上答题视为无效．‎ ‎3.可以使用科学计算器．‎ 一、选择题（以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在《答题卡》上填涂正确选项的字母框，每小题3分，共30分）‎ ‎1．如果“盈利10%”记为+10% ，那么“亏损6%”记为 ‎（A）-16%          （B）-6%         （C） +6%      （D） +4%‎ ‎2．2011年9月第九次全国少数民族传统体育运动会将在贵阳举行，为营造一个清洁、优美、‎ ‎ 舒适的美好贵阳，2011年3月贵阳启动了“自己动手，美化贵阳”活动，在活动过程中，志愿者们陆续发放了50000份倡议书.50000这个数用科学记数法表示为 ‎（A）　　　  （B）      （C）   　 （D）‎ ‎3．一枚质地均匀的正方体骰子，其六面上分别刻有1、2、3、4、5、6‎ 六个数字，投掷这个骰子一次，则向上一面的数字小于3的概率是 ‎（A） （B） （C） （D）‎ ‎4．一个几何体的三视图如图，则这个几何体是 ‎（A）圆锥 （B）三棱锥 （C）球 （D）圆锥 ‎5．某市甲、乙、丙、丁四支中学生足球队在市级联赛中进球数分别为 ‎ 7、7、6、5，则这组数据的众数是 ‎（A）5 （B）6 （C）7 （D）6.5‎ ‎6．如图，矩形的边长为2，边长为1，在 数轴上， 以原点为圆心，对角线的长为半径画弧，交 正半轴于一点，则这个点表示的实数是 ‎（A）2.5  （B） （C） （D）‎ ‎7．如图，中，，，，点在 边上的动点，则长不可能是 ‎（A）3.5        （B）4.2 ‎ ‎（C）5.8 （D）7‎ ‎8．如图所示，货车匀速通过隧道（隧道长大于货车长）‎ 时，货车从进入隧道至离开隧道的时间与货车在隧道 内的长度之间的关系用图象描述大致是（　　） ‎ ‎9．有下列五种正多边形地砖：①正三角形 ②正方形 ③正五边形 ④正六边形 ‎⑤正八边形.现要用同一种大小一样、形状相同的正多边形地砖铺设地面，其中能做到彼此之间不留空隙、不重叠地铺设的地砖有 ‎（A）4种 （B）3种 （C）2种 （D）1种 ‎10．如图，反比例函数和正比例函数的图象交于 ‎ 、两点，若，则的取值范围是 ‎ （A） （B）‎ ‎ （C）或 （D）或 二、填空题（每小题4分，共20分）‎ ‎11．如图，∥，交于， ‎ 则  ▲ 度.‎ ‎12．一次函数的图象不经过第 ▲ 象限．‎ ‎13．甲、乙两人分别在六次射击中的成绩如下表：（单位：环）‎ 这六次射击中成绩发挥比较稳定的是 ▲ .‎ ‎14．写出一个开口向下的二次函数的表达式 ▲ ．‎ ‎15．如图，已知等腰的直角边为1，以的斜 边为直角边，画第二个等腰，再以 的斜边为直角边，画第三个，…，依此类推直 到第五个 等腰，则由这五个第腰直角三角形所构成 的图形的面积为  ▲   .‎ 三、解答题 ‎16.（本题满分8分）‎ ‎ 在三个整式，，‎ 中，请你从中任意选择两个，将其中一个作为分子，另一个作为分母组成一个分式，并将这个分式进行化简，再求当时分式的值.‎ ‎17.（本题满分10分）‎ 贵阳某中学开展以“三创一办”为中心，以“校园文明”为主题的手抄报比赛，同学们积极参与，参赛同学每人交了一份得意作品，所有参赛作品均获奖，奖项分为一等奖、二等奖、三等奖和优秀奖，将获奖结果绘制成如下两幅统计图. ‎ 请你根据图中所给信息解答下列问题：‎ ‎ （1）一等奖所占的百分比是多少？(3分)‎ ‎（2）在此次比赛中，一共所到了多少份 参赛作品？请将条形统计图补充完整；(4分)‎ ‎（3）各奖项获奖学生分别有多少人？(3分)‎ ‎18.（本题满分10分）‎ ‎ 如图，点是正方形内一点，是等边三角形，连接、，延长交边于点.‎ ‎ （1）求证:；(5分)‎ ‎（2）求的度数.(5分)‎ ‎19.（本题满分10分）‎ ‎ 一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有3、4、5、.甲、乙两人每次同时从袋中各随机摸出1个小球，并计算摸出的这2个小球上数字之和，记录后都将小球放回袋中搅匀，进行重复实验.实验数据如下表：‎ 摸球总次数 ‎10‎ ‎20‎ ‎30‎ ‎60‎ ‎90‎ ‎120‎ ‎180‎ ‎240‎ ‎330‎ ‎450‎ ‎“和为8”出现的频率 ‎2‎ ‎10‎ ‎13‎ ‎24‎ ‎30‎ ‎37‎ ‎58‎ ‎82‎ ‎110‎ ‎150‎ ‎“和为8”出现的频率 ‎0.20‎ ‎0.50‎ ‎0.43‎ ‎0.40‎ ‎0.33‎ ‎0.31‎ ‎0.32‎ ‎0.34‎ ‎0.33‎ ‎0.33‎ ‎ 解答下列问题：‎ ‎ （1）如果实验继续进行下去，根据上表数据，出现“和为‎8”‎的频率将稳定在它的概率附近.估计出现“和为‎8”‎的概率是 ▲ .（4分）‎ ‎ （2）如果摸出的这两个小球上数字之和为9的概率是，那么的值可以取7吗？请用列表法或画树状图说明理由；如果的值不可以取7，请写出一个符合要求的值.（6分）‎ ‎20.（本题满分10分）‎ ‎ 某过街天桥的设计图是梯形（如图所示），桥面与地面平行，米，米.左斜面与地面的夹角为，右斜面与地面的夹角为，立柱于，立柱于，求桥面与地面之间的距离.（精确到‎0.1米）‎ ‎ ‎ ‎21.（本题满分10分）‎ ‎ 如图所示，二次函数的图象与轴的一个交点 为，另一个交点为，且与轴交于点.‎ ‎ （1）求的值；（3分）‎ ‎（2）求点的坐标；（3分）‎ ‎（3）该二次函数图象上有一点（其中，），‎ 使，求点坐标.（4分） ‎ ‎22.（本题满分10分）‎ ‎ 在□中，，，以为直径作 ‎⊙，边切⊙于点.‎ ‎（1）圆心到的距离是 ▲ . （4分）‎ ‎（2）求由弧、线段、所围成的阴影部分的面积.（结果保留和根号）（6分）‎ ‎23.（本题满分10分） ‎ ‎ 童星玩具厂工人的工作时间为：每月22天，每天8小时.工资待遇为：按件计酬，多劳多得，每月另加福利工资500元，按月结算.该厂生产、两种产品，工人每生产一件种产品可得报酬1.50元，每生产一件种产品可得报酬2.80元.该厂工人可以选择、两种产品中的一种或两种进行生产.工人小李生产1件产品和1件产品需35分钟；生产3件产品和2件产品需85分钟.‎ ‎ （1）小李生产1件产品的需要 ▲ 分钟，生产1件产品的需要 ▲ 分钟.（4分）‎ ‎（2）求小李每月的工资收入范围.（6分）‎ ‎24.（本题满分12分）‎ ‎ [阅读]在平面直角坐标系中，以任意两点、‎ 为端点的线段中点坐标为.‎ ‎ [运用]‎ ‎ （1）如图，矩形的对角线相交于点，、在轴和轴上，坐标原点，点的坐标为，则点的坐标为 ▲ ；（4分）‎ ‎（2）在直角坐标系中，有，，三点，另有一点与、、构成平行四边形的顶点，求点的坐标.（6分）‎ ‎25.（本题满分12分）‎ ‎ 用长度一定的不锈钢材料设计成外观为矩形的框架（如图①②③中的一种）.‎ ‎ 设竖档米，请根据以上图案回答下列问题：（题中的不锈钢材料总长均指各图中所有黑线的长度和，所有横档和竖档分别与、平行）‎ ‎ （1）在图①中，如果不锈钢材料总长度为‎12米，当为多少时，矩形框架的面积为3平方米？（4分）‎ ‎ （2）在图②中，如果不锈钢材料总长度为‎12米，当为多少时，矩形框架的面积最大？最大面积是多少？（4分）‎ ‎（3）在图③中，如果不锈钢材料总长度为米，共有条竖档，那么当为多少时，矩形框架的面积最大？最大面积是多少？‎