中考复习14——圆证明解答题

中考复习14——圆证明解答题

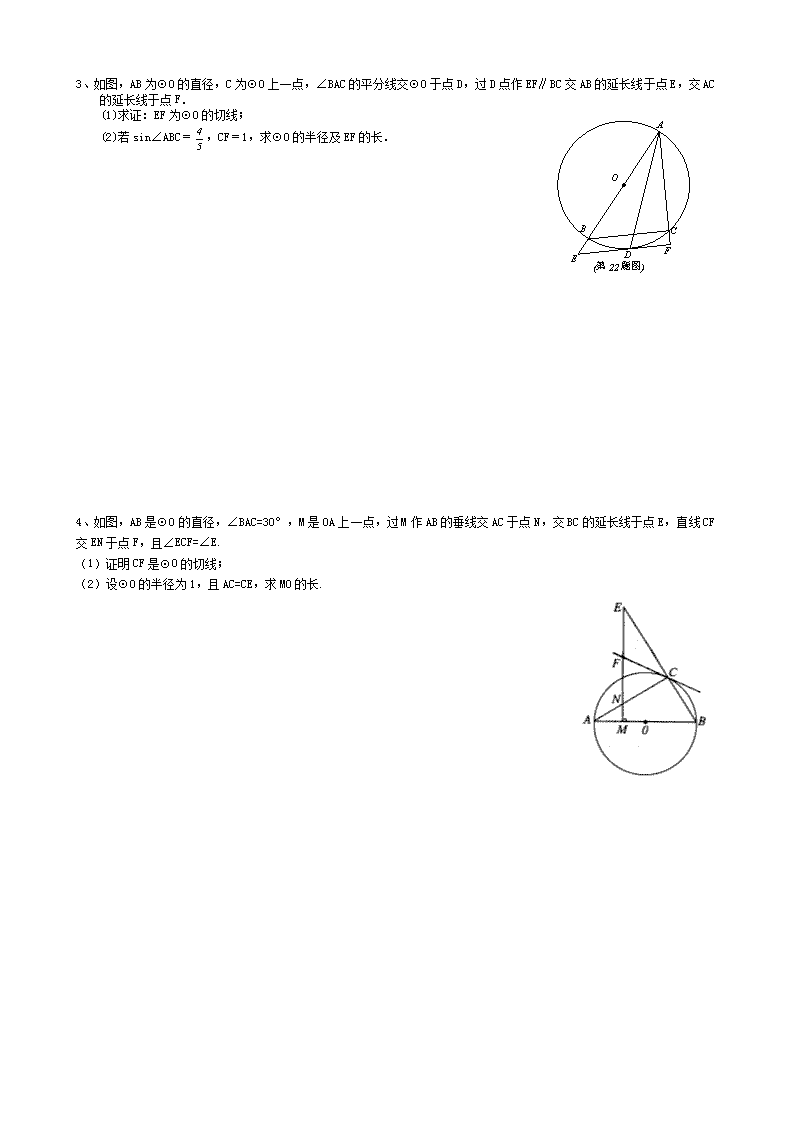
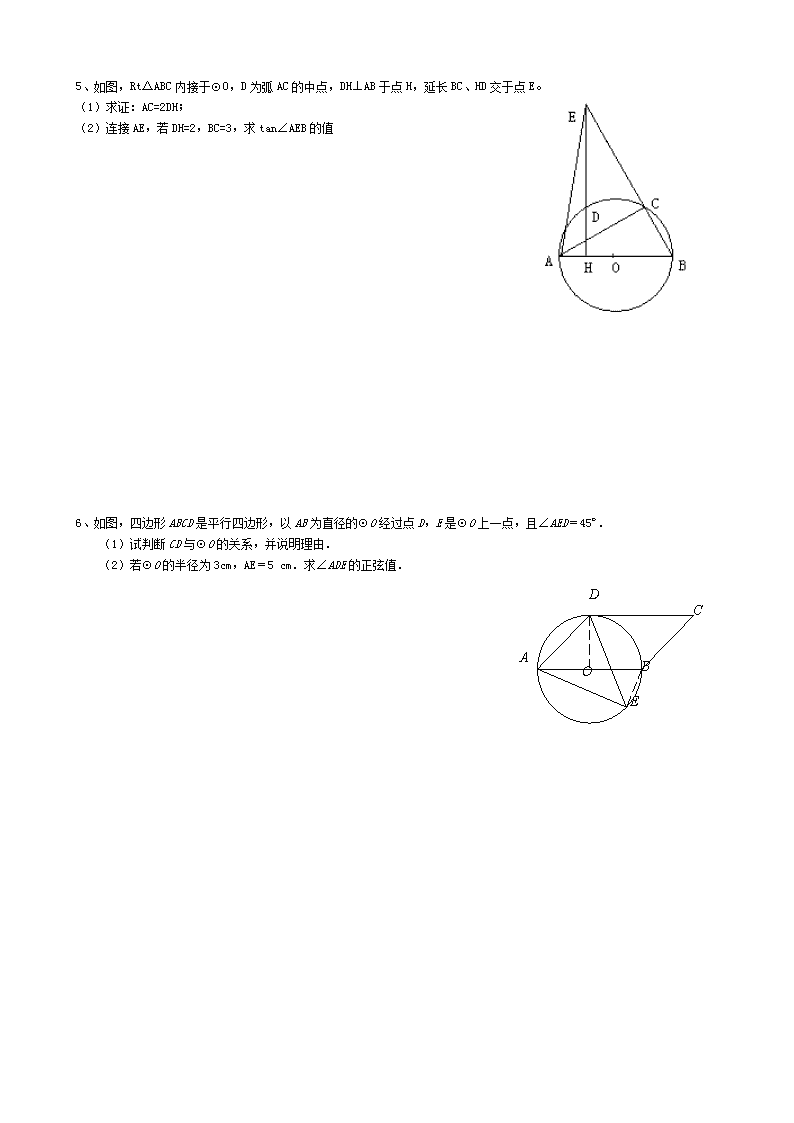
‎ 2012年中考复习（十四）——圆证明、解答题 ‎1、如图，是以为直径的上一点，于点，过点作的切线，与的延长线相交于点是的中点，连结并延长与相交于点，延长与的延长线相交于点．‎ O D G C A E F B P ‎（1）求证：；‎ ‎（2）求证：是的切线；‎ ‎2、如图，AB、BC、CD分别与⊙O切于E、F、G，且AB∥CD．连接OB、OC，延长CO交⊙O于点M，过点M作MN∥OB交CD于N．‎ ‎⑴求证：MN是⊙O的切线；‎ ‎⑵当0B=6cm，OC=8cm时，求⊙O的半径及MN的长．‎ ‎ ‎ ‎ ‎ ‎3、如图，AB为⊙O的直径，C为⊙O上一点，∠BAC的平分线交⊙O于点D，过D点作EF∥BC交AB的延长线于点E，交AC的延长线于点F．‎ A B C D E F O ‎(第22题图)‎ ‎(1)求证：EF为⊙O的切线；‎ ‎(2)若sin∠ABC＝，CF＝1，求⊙O的半径及EF的长．‎ ‎4、如图，AB是⊙O的直径，∠BAC=30°，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，且∠ECF=∠E.‎ ‎（1）证明CF是⊙O的切线；‎ ‎（2）设⊙O的半径为1，且AC=CE，求MO的长.‎ ‎ ‎ ‎5、如图，Rt△ABC内接于⊙O，D为弧AC的中点，DH⊥AB于点H，延长BC、HD交于点E。‎ ‎（1）求证：AC=2DH；‎ ‎（2）连接AE，若DH=2，BC=3，求tan∠AEB的值 ‎6、如图，四边形ABCD是平行四边形，以AB为直径的⊙O经过点D，E是⊙O上一点，且∠AED＝45º．‎ ‎ （1）试判断CD与⊙O的关系，并说明理由．‎ ‎（2）若⊙O的半径为3cm，AE＝5 cm．求∠ADE的正弦值．‎ ‎ ‎A B C D E O A B C E D O M ‎7、已知：如图，在半径为4的⊙O中，AB，CD是两条直径，M为OB的中点，CM的延长线交⊙O于点E，且EM＞MC．连结DE，DE=.‎ ‎（1）求证：；‎ ‎（2） 求EM的长；‎ ‎（3）求sin∠EOB的值.‎ ‎8、如图，AB为⊙O的直径，弦CD⊥AB于点H，E为AB延长线上一点，CE交⊙O于F。‎ ‎（1）求证：BF平分∠DFE；‎ ‎（2）若EF=DF=4，BE=5，CH=3，求⊙O的半径 ‎9、如图，⊙的直径是，过点的直线是⊙的切线，、是⊙上的两点，连接、、和．‎ ‎(1)求证：；‎ ‎(2)若是的平分线，且，求的长．‎ ‎10、如图，BD是⊙O的直径，OA⊥OB,M是劣弧上一点，过点M作⊙O的切线MP交OA的延长线于P点，MD与OA交于点N。‎ ‎（1）求证：PM=PN；‎ ‎（2）若BD=4,PA=AO,过B点作BC∥MP交⊙O于C点，求BC的长．‎ ‎ ‎ ‎11、如图，以△ABC的边BC为直径作⊙O分别交AB、AC于D、E两点，过B、C两点分别作DE的垂线，垂足分别为M、N。‎ ‎（1）求证：DM=EN ‎（2）过A作AH⊥BC于点H，若=2，求的值 ‎12、如图，在Rt△ABC中，∠BCA=900，以斜边AB上一点O为圆心，OB为半径作⊙O，⊙O切AC于E，交AB于D。‎ ‎（1）求证：△BCE∽△BED ‎（2）若CE=3，AE=5，求△ADE的面积 ‎（3）若CE=3，AE=5，求tan∠ABE的值 ‎（4）连接OC交BE于F，若=，求的值。‎ ‎13、如图，⊙O是△ABC的外接圆，FH是⊙O 的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．‎ H ‎（1）证明：AF平分∠BAC；‎ ‎（2）证明：BF＝FD；‎ ‎（3）若EF＝4，DE＝3，求AD的长．‎ ‎14、如图，是圆的直径，厘米，是圆的切线，为切点．过作，交于点，连结．‎ A P D B C O ‎（1）求证；‎ ‎（2）若切线的长为12厘米，求弦的长．‎ ‎15、如图，在△ABC中，∠BAC=90°，BM平分∠ABC交AC于M，以A为圆心，AM为半径作OA交BM于N，AN的延长线交BC于D，直线AB交OA于P、K两点．作MT⊥BC于T ‎(1)求证AK=MT； ‎ ‎(2)求证：AD⊥BC；‎ ‎(3)当AK=BD时， 求证：．‎ ‎ ‎ ‎16、如图，⊙O的半径OD经过弦AB(不是直径)的中点C，过AB的延长线上一点P作⊙O的切线PE，E为切点，PE∥OD；延长直径AG交PE于点H；直线DG交OE于点F，交PE于点K．‎ ‎(第16题)‎ ‎（1）求证：四边形OCPE是矩形；‎ ‎（2）求证：HK＝HG；‎ ‎（3）若EF＝2，FO＝1，求KE的长．‎