2010年四川省成都市中考数学试题

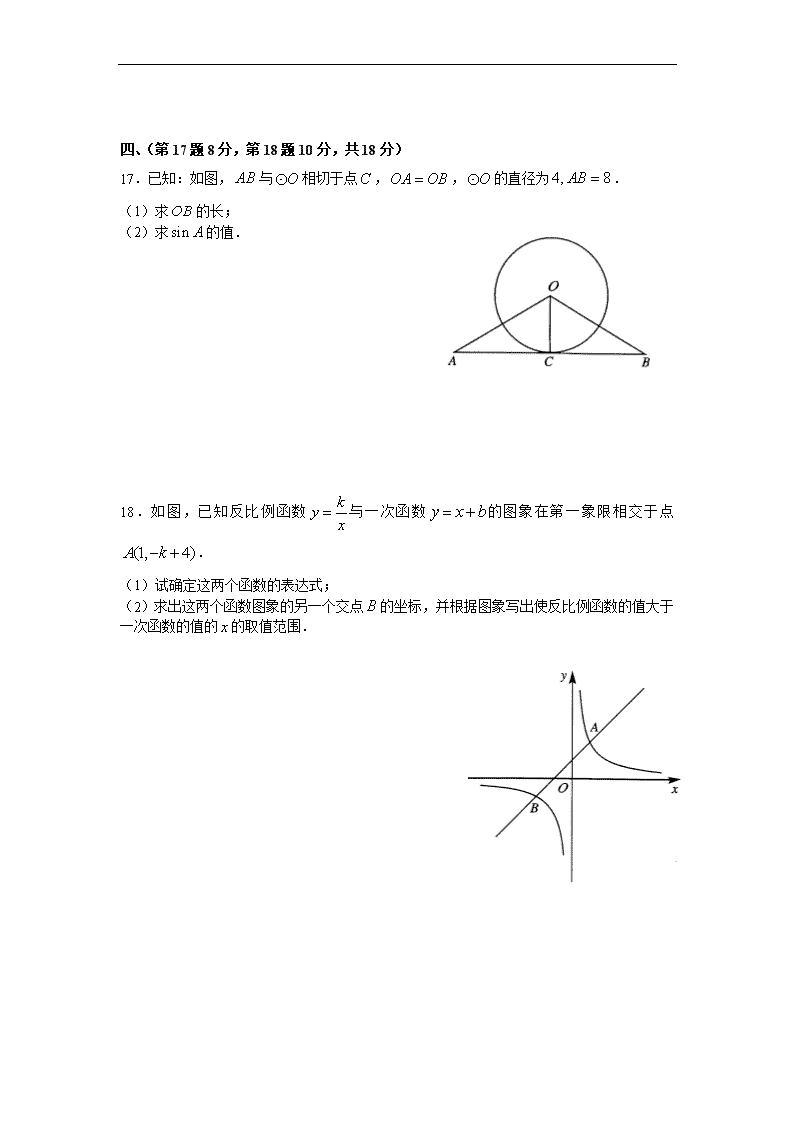
2010年四川省成都市中考数学试题

‎2010年成都市中考数学试题 A卷（共100分）‎ 一、选择题：（每小题3分，共15分）‎ ‎1．下列各数中，最大的数是（ ）‎ ‎（A） （B） （C） （D）‎ ‎2．表示（ ）‎ ‎（A） （B） （C） （D）‎ ‎3．上海“世博会”吸引了来自全球众多国家数以千万的人前来参观．据统计，2010年5月某日参观世博园的人数约为256 000，这一人数用科学记数法表示为（ ）‎ ‎（A） （B） （C） （D）‎ ‎4．如图是一个几何体的三视图，则这个几何体的形状是（ ）‎ ‎（A）圆柱 （B）圆锥 （C）圆台 （D）长方体 ‎5．把抛物线向右平移1个单位，所得抛物线的函数表达式为（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎6．如图，已知，，则的度数为（ ）‎ ‎（A） （B） ‎ ‎（C） （D）‎ ‎7．为了解某班学生每天使用零花钱的情况，小红随机调查了15名同学，结果如下表：‎ 每天使用零花钱 ‎（单位：元）‎ ‎1‎ ‎2‎ ‎3‎ ‎5‎ ‎6‎ 人 数 ‎2‎ ‎5‎ ‎4‎ ‎3‎ ‎1‎ 则这15名同学每天使用零花钱的众数和中位数分别是（ ）‎ ‎（A）3，3 （B）2，3 （C）2，2 （D）3，5‎ ‎8．已知两圆的半径分别是4和6，圆心距为7，则这两圆的位置关系是（ ）‎ ‎（A）相交 （B）外切 （C）外离 （D）内含 ‎9．若一次函数的函数值随的增大而减小，且图象与轴的负半轴相交，那么对和的符号判断正确的是（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎10．已知四边形，有以下四个条件：①；②；③；④．从这四个条件中任选两个，能使四边形成为平行四边形的选法种数共有（ ）‎ ‎（A）6种 （B）5种 （C）4种 （D）3种 二、填空题：（每小题3分，共15分）‎ ‎11．在平面直角坐标系中，点位于第___________象限．‎ ‎12．若为实数，且，则的值为___________．‎ ‎13．如图，在中，为的直径，，‎ 则的度数是_____________度．‎ ‎14．甲计划用若干天完成某项工作，在甲独立工作两天后，乙加入此项工作，且甲、乙两人工效相同，结果提前两天完成任务．设甲计划完成此项工作的天数是，则的值是_____________．‎ ‎15．若一个圆锥的侧面积是，侧面展开图是半圆，则该圆锥的底面圆半径是___________．‎ 三、（第1小题7分，第2小题8分，共15分）‎ ‎16．解答下列各题：‎ ‎（1）计算：．‎ ‎（2）若关于的一元二次方程有两个实数根，求的取值范围及的非负整数值.‎ 四、（第17题8分，第18题10分，共18分）‎ ‎17．已知：如图，与相切于点，，的直径为．‎ ‎（1）求的长；‎ ‎（2）求的值．‎ ‎18．如图，已知反比例函数与一次函数的图象在第一象限相交于点．‎ ‎（1）试确定这两个函数的表达式；‎ ‎（2）求出这两个函数图象的另一个交点的坐标，并根据图象写出使反比例函数的值大于一次函数的值的的取值范围．‎ 五、（第19题10分，第20题12分，共22分）‎ ‎19．某公司组织部分员工到一博览会的五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示． ‎ 请根据统计图回答下列问题：‎ ‎（1）将条形统计图和扇形统计图在图中补充完整； ‎ ‎（2）若馆门票仅剩下一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，将牌放回洗匀背面朝上放置在桌面上，再由另一人抽．若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华．” 请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平． ‎ ‎20．已知：在菱形中，是对角线上的一动点．‎ ‎（1）如图甲，为线段上一点，连接并延长交于点，当是的中点时，求证：；‎ ‎（2）如图乙，连结并延长，与交于点，与的延长线交于点．若，求和的长．‎ B卷（共50分）‎ 一、填空题：（每小题4分，共20分）‎ ‎21．设，是一元二次方程的两个实数根，则的值为__________________．‎ ‎22．如图，在中，，，‎ ‎，动点从点开始沿边向以 的速度移动（不与点重合），动点从点 开始沿边向以的速度移动（不与点 重合）．如果、分别从、同时出发，那么 经过_____________秒，四边形的面积最小．‎ ‎23．有背面完全相同，正面上分别标有两个连续自然数（其中）的卡片20张．小李将其混合后，正面朝下放置在桌面上，并从中随机地抽取一张，则该卡片上两个数的各位数字之和（例如：若取到标有9，10的卡片，则卡片上两个数的各位数字之和为）不小于14的概率为_________________.‎ ‎24．已知是正整数，是反比例函数图象上的一列点，其中．记，，若（是非零常数），则的值是________________________（用含和的代数式表示）．‎ ‎25．如图，内接于，，‎ 是上与点关于圆心成中心对称的点，是 边上一点，连结．已知，‎ ‎，是线段上一动点，连结并延长交 四边形的一边于点，且满足，则 的值为_______________．‎ 二、（共8分）‎ ‎26．随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭，成为居民消费新的增长点．据某市交通部门统计，2007年底全市汽车拥有量为180万辆，而截止到2009年底，全市的汽车拥有量已达216万辆．‎ ‎ （1）求2007年底至2009年底该市汽车拥有量的年平均增长率；‎ ‎ （2）为保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2011年底全市汽车拥有量不超过231.96万辆；另据估计，从2010年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的10％．假定每年新增汽车数量相同，请你计算出该市每年新增汽车数量最多不能超过多少万辆．‎ 三、（共10分）‎ ‎27．已知：如图，内接于，为直径，弦于，是的中点，连结并延长交的延长线于点，连结，分别交、于点、．‎ ‎ （1）求证：是的外心；‎ ‎ （2）若,求的长；‎ ‎ （3）求证：．‎ 四、（共12分）‎ ‎28．在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），与轴交于点，点的坐标为，若将经过两点的直线沿轴向下平移3个单位后恰好经过原点，且抛物线的对称轴是直线．‎ ‎（1）求直线及抛物线的函数表达式；‎ ‎（2）如果P是线段上一点，设、的面积分别为、，且，求点P的坐标；‎ ‎（3）设的半径为l，圆心在抛物线上运动，则在运动过程中是否存在与坐标轴相切的情况？若存在，求出圆心的坐标；若不存在，请说明理由．并探究：若设⊙Q的半径为，圆心在抛物线上运动，则当取何值时，⊙Q与两坐轴同时相切？‎ 成都市2010年中考数学答案 一、 选择题：（每小题3分，共30分）‎ ‎⒈D ⒉C ⒊A ⒋B ⒌D ⒍B ⒎B ⒏A ⒐D ⒑C 二、 填空题：（每小题3分，共15分）‎ ‎⒒ 四； ⒓ 1； ⒔ 100； ⒕ 6； ⒖ 3‎ 三、 ‎（第1小题7分，第2小题8分，共15分）‎ ‎16．.（1）解：原式==3‎ ‎（2）解：∵关于的一元二次方程有两个实数根，‎ ‎ ∴△=‎ ‎ 解得 ‎ ∴的非负整数值为0,1,2。‎ 四、 ‎（第17题8分，第18题10分，共18分）‎ ‎17．.解：（1）由已知，OC=2，BC=4。‎ ‎ 在Rt△OBC中，由勾股定理，得 ‎ ‎ ‎ （2）在Rt△OAC中，∵OA=OB=，OC=2，‎ ‎ ∴sinA=‎ ‎18.解：（1）∵已知反比例函数经过点，‎ ‎ ∴，即 ‎ ∴‎ ‎∴A(1，2)‎ ‎∵一次函数的图象经过点A(1，2)，‎ ‎∴‎ ‎∴‎ ‎∴反比例函数的表达式为，‎ 一次函数的表达式为。‎ ‎（2）由消去，得。‎ 即,∴或。‎ ‎∴或。‎ ‎∴或 ‎∵点B在第三象限，∴点B的坐标为。‎ 由图象可知，当反比例函数的值大于一次函数的值时，的取值范围是或。‎ 一、 ‎（第19题10分，第20题12分，共22分）‎ ‎19..解：（1）‎ B馆门票为50张，C占15%。‎ 开始 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1 2 3 4‎ ‎1 2 3 4‎ ‎1 2 3 4‎ ‎1 2 3 4‎ 小明 小华 ‎（2）画树状图 或列表格法。‎ 小华抽到 的数字 小明抽到 的数字 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎（1,1）‎ ‎（1,2）‎ ‎（1,3）‎ ‎（1,4）‎ ‎2‎ ‎（2,1）‎ ‎（2,2）‎ ‎（2,3）‎ ‎（2,4）‎ ‎3‎ ‎（3,1）‎ ‎（3,2）‎ ‎（3,3）‎ ‎（3,4）‎ ‎4‎ ‎（4,1）‎ ‎（4,2）‎ ‎（4,3）‎ ‎（4,4）‎ 共有16种可能的结果，且每种结果的可能性相同，其中小明可能获得门票的结果有6种，分别是（2,1），（3,1），（3,2），（4,1），（4,2），（4,3）。‎ ‎∴小明获得门票的概率，‎ ‎ 小华获得门票的概率。‎ ‎∵‎ ‎∴这个规则对双方不公平。‎ ‎20. （1）证明：∵ABCD为菱形，∴AD∥BC。‎ ‎ ∴∠OBP=∠ODQ ‎ ∵O是是的中点，‎ ‎ ∴OB=OD ‎ 在△BOP和△DOQ中，‎ ‎ ∵∠OBP=∠ODQ，OB=OD，∠BOP=∠DOQ ‎∴△BOP≌△DOQ（ASA）‎ ‎∴OP=OQ。‎ ‎（2）解：如图，过A作AT⊥BC，与CB的延长线交于T.‎ ‎∵ABCD是菱形，∠DCB=60°‎ ‎∴AB=AD=4，∠ABT=60°‎ ‎∴AT=ABsin60°=‎ TB=ABcos60°=2‎ ‎∵BS=10，∴TS=TB+BS=12，‎ ‎∴AS=。‎ ‎∵AD∥BS，∴△AOD∽△SOB。‎ ‎∴，‎ 则,∴‎ ‎∵AS=，∴。‎ 同理可得△ARD∽△SRC。‎ ‎∴,‎ 则,∴，‎ ‎∴。‎ ‎∴OR=OS-RS=。‎ B卷（共50分）‎ 一、 填空题：（每小题4分，共20分）‎ ‎21. 7； 22. 3； 23. ； 24. 25. 1和 二、 ‎（共8分）‎ ‎26.. 解：（1）设该市汽车拥有量的年平均增长率为。根据题意，得 ‎ ‎ 解得，（不合题意，舍去）。‎ 答：该市汽车拥有量的年平均增长率为20%。‎ ‎（2）设全市每年新增汽车数量为万辆，则2010年底全市的汽车拥有量为万辆，2011年底全市的汽车拥有量为万辆。根据题意得 解得 答：该市每年新增汽车数量最多不能超过30万辆。‎ 三、 ‎（共10分）‎ ‎27. （1）证明：∵C是的中点，∴，‎ ‎∴∠CAD=∠ABC ‎∵AB是⊙O的直径，∴∠ACB=90°。‎ ‎∴∠CAD+∠AQC=90°‎ 又CE⊥AB，∴∠ABC+∠PCQ=90°‎ ‎∴∠AQC=∠PCQ ‎∴在△PCQ中，PC=PQ，‎ ‎∵CE⊥直径AB，∴‎ ‎∴‎ ‎∴∠CAD=∠ACE。‎ ‎∴在△APC中，有PA=PC，‎ ‎∴PA=PC=PQ ‎∴P是△ACQ的外心。‎ ‎（2）解：∵CE⊥直径AB于F，‎ ‎∴在Rt△BCF中，由tan∠ABC=，CF=8，‎ 得。‎ ‎∴由勾股定理，得 ‎∵AB是⊙O的直径，‎ ‎∴在Rt△ACB中，由tan∠ABC=，‎ ‎ 得。‎ 易知Rt△ACB∽Rt△QCA，∴‎ ‎∴。‎ ‎（3）证明：∵AB是⊙O的直径，∴∠ACB=90°‎ ‎∴∠DAB+∠ABD=90°‎ 又CF⊥AB，∴∠ABG+∠G=90°‎ ‎∴∠DAB=∠G；‎ ‎∴Rt△AFP∽Rt△GFB，‎ ‎∴，即 易知Rt△ACF∽Rt△CBF，‎ ‎∴（或由摄影定理得）‎ ‎∴‎ 由（1），知PC=PQ，∴FP+PQ=FP+PC=FC ‎∴。‎ 一、 ‎（共12分）‎ ‎28. （1）解：（1）∵沿轴向下平移3个单位后恰好经过原点，‎ ‎ ∴，。‎ ‎ 将 代入，得。解得。‎ ‎ ∴直线AC的函数表达式为。‎ ‎ ∵抛物线的对称轴是直线 ‎∴解得 ‎∴抛物线的函数表达式为。‎ ‎（2）如图，过点B作BD⊥AC于点D。‎ ‎ ∵，‎ ‎∴ ‎ ‎∴。‎ 过点P作PE⊥x轴于点E，‎ ‎∵PE∥CO，∴△APE∽△ACO，‎ ‎∴，‎ ‎∴‎ ‎∴，解得 ‎∴点P的坐标为 ‎（3）（Ⅰ）假设⊙Q在运动过程中，存在与坐标轴相切的情况。‎ ‎ 设点Q的坐标为。‎ ① 当⊙Q与y轴相切时，有，即。‎ 当时，得，∴‎ 当时，得，∴‎ ① 当⊙Q与x轴相切时，有，即 当时，得，即，解得，∴‎ 当时，得，即，解得，∴，。‎ 综上所述，存在符合条件的⊙Q，其圆心Q的坐标分别为，，，，。‎ ‎（Ⅱ）设点Q的坐标为。‎ 当⊙Q与两坐标轴同时相切时，有。‎ 由，得，即，‎ ‎∵△=‎ ‎∴此方程无解。‎ 由，得，即，‎ 解得 ‎∴当⊙Q的半径时，⊙Q与两坐标轴同时相切。‎