中考数学抛物线压轴题

中考数学抛物线压轴题

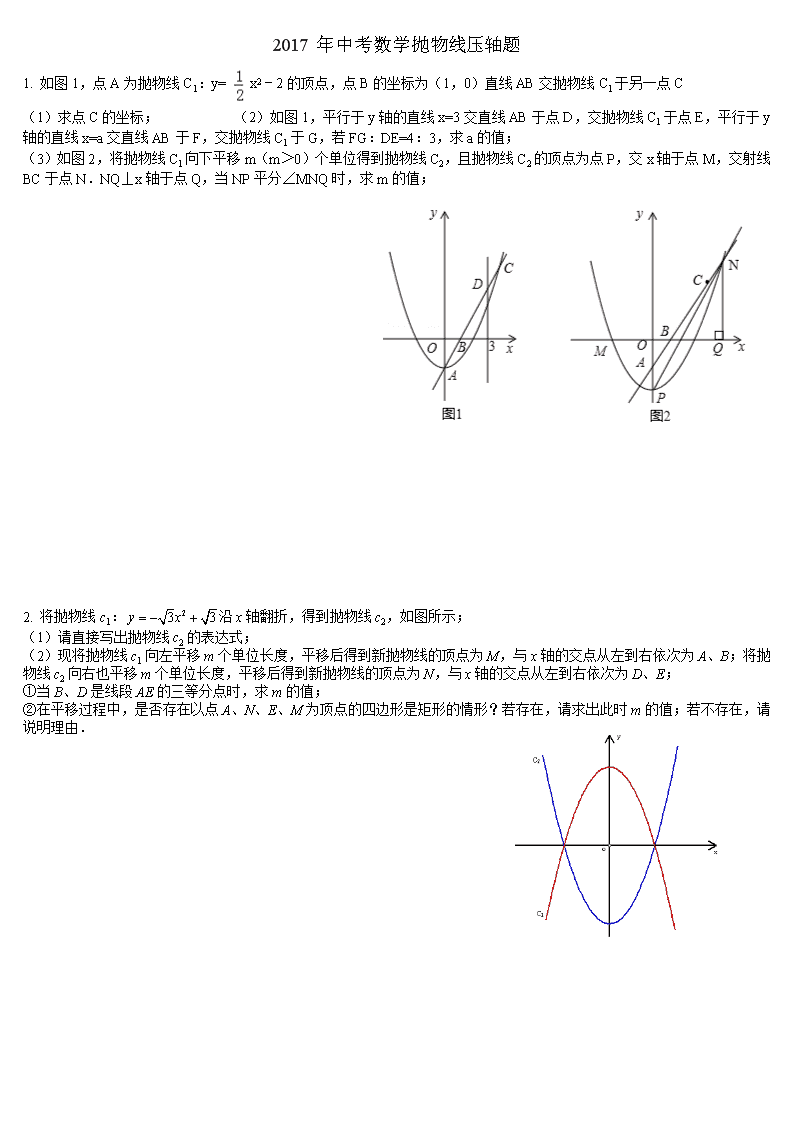
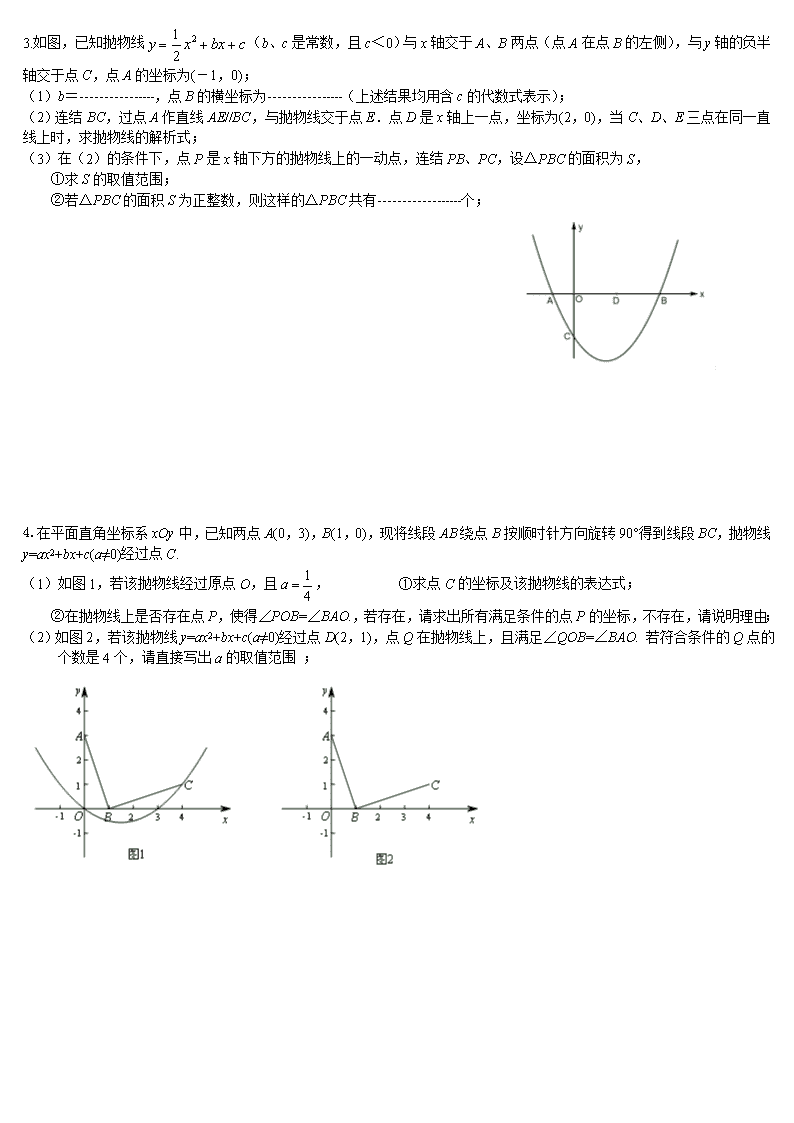
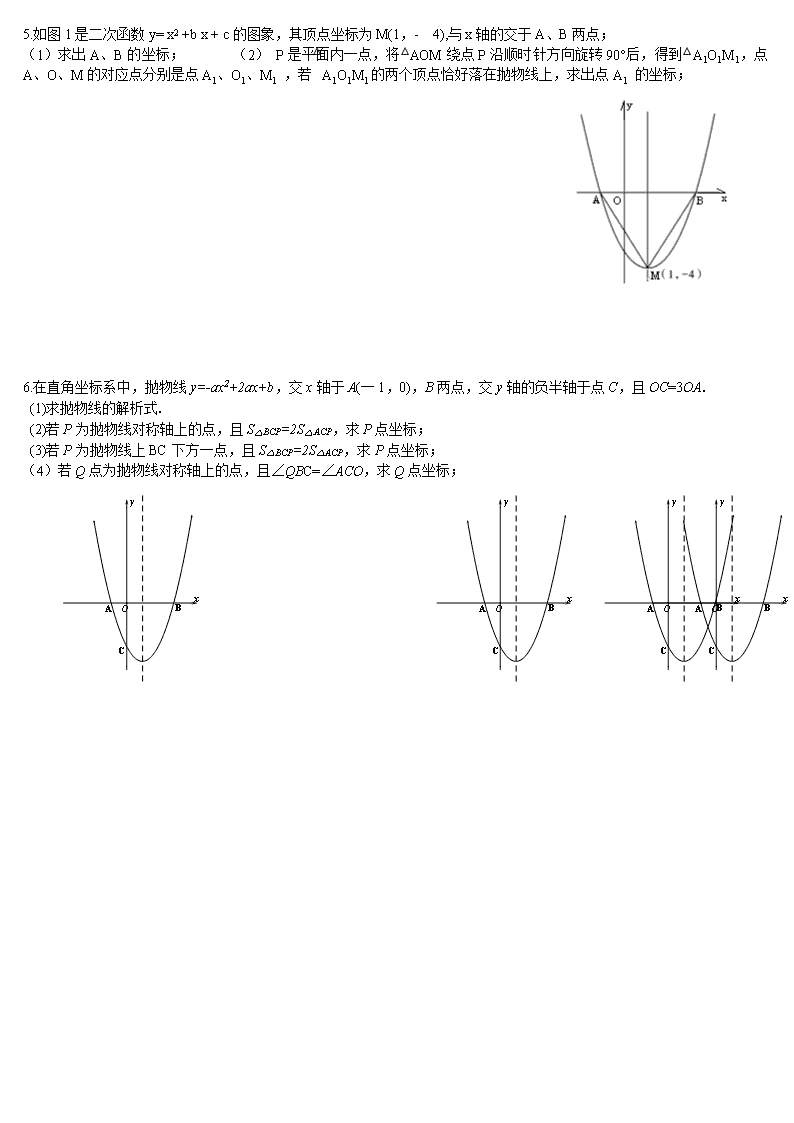
‎2017年中考数学抛物线压轴题 ‎1. 如图1，点A为抛物线C1：y= x2﹣2的顶点，点B的坐标为（1，0）直线AB交抛物线C1于另一点C ‎（1）求点C的坐标； （2）如图1，平行于y轴的直线x=3交直线AB于点D，交抛物线C1于点E，平行于y轴的直线x=a交直线AB于F，交抛物线C1于G，若FG：DE=4：3，求a的值；‎ ‎（3）如图2，将抛物线C1向下平移m（m＞0）个单位得到抛物线C2，且抛物线C2的顶点为点P，交x轴于点M，交射线BC于点N．NQ⊥x轴于点Q，当NP平分∠MNQ时，求m的值；‎ ‎2. 将抛物线c1：沿x轴翻折，得到抛物线c2，如图所示；‎ ‎（1）请直接写出抛物线c2的表达式；‎ ‎（2）现将抛物线c1向左平移m个单位长度，平移后得到新抛物线的顶点为M，与x轴的交点从左到右依次为A、B；将抛物线c2向右也平移m个单位长度，平移后得到新抛物线的顶点为N，与x轴的交点从左到右依次为D、E；‎ ‎①当B、D是线段AE的三等分点时，求m的值；‎ ‎②在平移过程中，是否存在以点A、N、E、M为顶点的四边形是矩形的情形？若存在，请求出此时m的值；若不存在，请说明理由．‎ ‎3.如图，已知抛物线（b、c是常数，且c＜0）与x轴交于A、B两点（点A在点B的左侧），与y轴的负半轴交于点C，点A的坐标为(－1，0)；‎ ‎（1）b＝----------------，点B的横坐标为----------------（上述结果均用含c的代数式表示）；‎ ‎（2）连结BC，过点A作直线AE//BC，与抛物线交于点E．点D是x轴上一点，坐标为(2，0)，当C、D、E三点在同一直线上时，求抛物线的解析式；‎ ‎（3）在（2）的条件下，点P是x轴下方的抛物线上的一动点，连结PB、PC，设△PBC的面积为S，‎ ‎①求S的取值范围；‎ ‎②若△PBC的面积S为正整数，则这样的△PBC共有------------------个；‎ ‎4.在平面直角坐标系xOy中，已知两点A(0，3)，B(1，0)，现将线段AB绕点B按顺时针方向旋转90°得到线段BC，抛物线y=ax2+bx+c(a≠0)经过点C.‎ ‎（1）如图1，若该抛物线经过原点O，且， ①求点C的坐标及该抛物线的表达式；‎ ‎②在抛物线上是否存在点P，使得∠POB=∠BAO.，若存在，请求出所有满足条件的点P的坐标，不存在，请说明理由；‎ ‎（2）如图2，若该抛物线y=ax2+bx+c(a≠0)经过点D(2，1)，点Q在抛物线上，且满足∠QOB=∠BAO. 若符合条件的Q点的个数是4个，请直接写出a的取值范围 ；‎ ‎5.如图1是二次函数y= x2 +b x + c的图象，其顶点坐标为M(1，- 4),与x轴的交于A、B两点；‎ ‎（1）求出A、B的坐标； （2） P是平面内一点，将△AOM绕点P沿顺时针方向旋转90°后，得到△A1O‎1M1，点A、O、M的对应点分别是点A1、O1、M1 ，若△A1O‎1M1的两个顶点恰好落在抛物线上，求出点A1 的坐标； ‎ ‎6.在直角坐标系中，抛物线y=-ax2+2ax+b，交x轴于A(一1，0)，B两点，交y轴的负半轴于点C，且OC=3OA.‎ ‎(1)求抛物线的解析式.‎ ‎(2)若P为抛物线对称轴上的点，且S△BCP=2S△ACP，求P点坐标；‎ ‎(3)若P为抛物线上BC下方一点，且S△BCP=2S△ACP，求P点坐标；‎ ‎（4）若Q点为抛物线对称轴上的点，且∠QBC=∠ACO，求Q点坐标；‎ ‎7. 已知抛物线C1的顶点为P（1， 0），且过点（0，），将抛物线C1向下平移h个单位（h>0）得到抛物线C2；一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m>0）； ⑴求抛物线C1的解析式的一般形式； ‎ ‎ ⑵当m=2时，求h的值；‎ ‎⑶若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F，求证：的值为定值，并求此定值；‎ ‎8.如图，已知抛物线y=x2-2x-3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，该抛物线顶点为D，对称轴交x轴于点H；⑴求A，B两点的坐标； ⑵设点P在x轴下方的抛物线上，当∠ABP=∠CDB时，求出点P的坐标； ⑶以OB为边在第四象限内作等边△OBM，设点E为x轴的正半轴上一动点（OE>OH），连接ME，把线段ME绕点M顺时针旋转60°得MF，求线段DF的最小值；‎ ‎9.已知抛物线C1：y=ax2+bx+（a≠0）经过点A（﹣1，0）和B（3，0）；‎ ‎（1）求抛物线C1的解析式，并写出其顶点C的坐标； （2）如图1，把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2，此时点A，C分别平移到点D，E处．设点F在抛物线C1上且在x轴的下方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标； （3）如图2，在（2）的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，点P为线段MN的中点，当点M从点B向点C运动时：tan∠ENM的值如何变化？请说明理由；‎ ‎10. 如图，坐标系在Rt△AOB中，∠BAO=90°，O为坐标原点，B在x轴正半轴上，A在第一象限，OA=3，AB= 4； ‎ ‎ ⑴求直线AB的解析式； ⑵将△AOB沿垂直于x轴的线段折叠（点C在x轴上，且不与点B重合，点D在线段AB上），使点B落在x轴上，对应点为E，设点C的坐标为（x，0），设△CDE与△AOB重合部分的面积为S，直接写出S与C点的横坐标x之间的函数关系式（包括自变量x的取值范围）； ‎