中考数学试题汇编——阅读理解型

中考数学试题汇编——阅读理解型

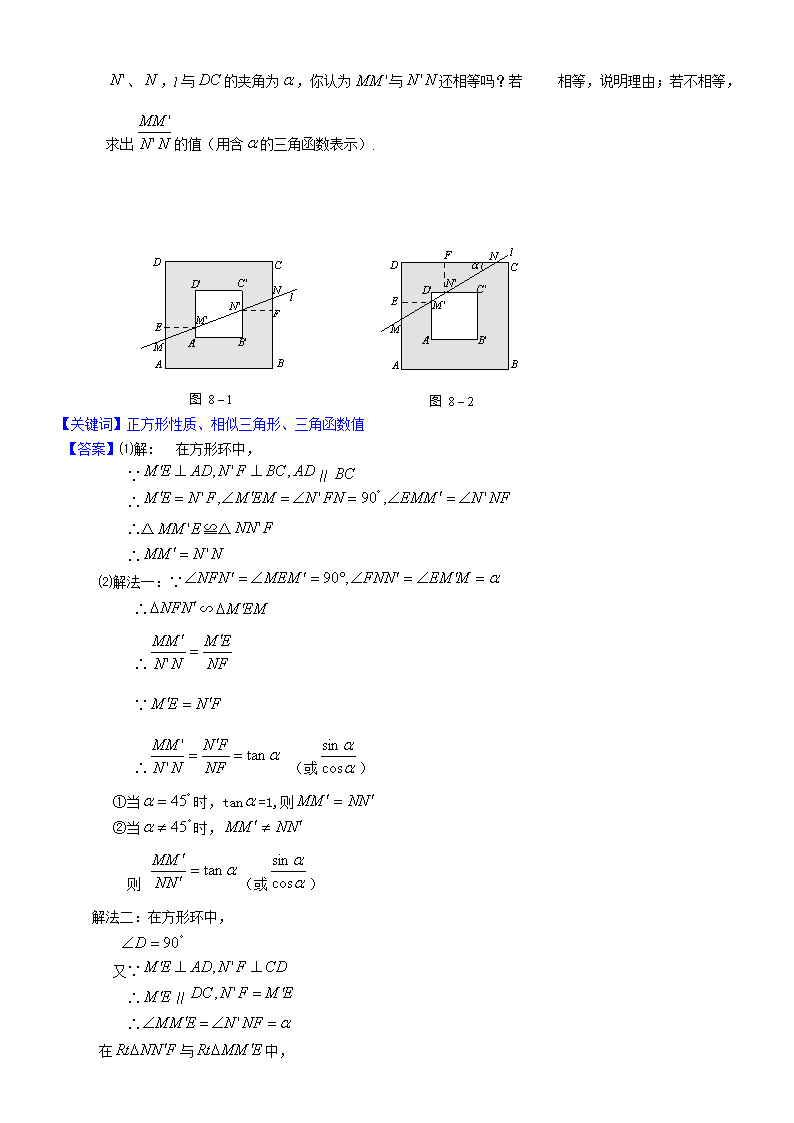
‎2010年中考数学试题分类汇编 阅读理解型 ‎15．（2010年浙江省东阳县）阅读材料，寻找共同存在的规律：有一个运算程序a⊕b = n，‎ 可以使：（a+c）⊕b= n+c，a⊕（b+c）=n－2c，‎ 如果1⊕1=2，那么2010⊕2010 = ．‎ ‎【关键词】阅读理解 ‎【答案】-2007‎ ‎22．（2010年山东省青岛市）某市政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：．‎ ‎（1）设李明每月获得利润为w（元），当销售单价定为多少元时，每月可获得最大利 润？‎ ‎（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？‎ ‎（3）根据物价部门规定，这种护眼台灯的销售单价不得高于32元，如果李明想要每月获得的利润不低于2000元，那么他每月的成本最少需要多少元？‎ ‎（成本＝进价×销售量）‎ ‎【关键词】函数的应用 ‎【答案】解：（1）由题意，得：w = (x－20)·y ‎=(x－20)·()‎ ‎.‎ 答：当销售单价定为35元时，每月可获得最大利润． 3分 ‎（2）由题意，得：‎ 解这个方程得：x1 = 30，x2 = 40．‎ 答：李明想要每月获得2000元的利润，销售单价应定为30元或40元.‎ 法二：∵，‎ ‎∴抛物线开口向下.‎ ‎∴当30≤x≤40时，w≥2000．‎ ‎∵x≤32，‎ ‎∴30≤x≤32时，w≥2000．‎ ‎∵，，‎ ‎∴y随x的增大而减小.‎ ‎∴当x = 32时，y最小＝180.‎ ‎∵当进价一定时，销售量越小，‎ 成本越小，‎ ‎∴（元）.‎ ‎ 6分 ‎（3）法一：∵，‎ ‎∴抛物线开口向下.‎ ‎∴当30≤x≤40时，w≥2000．‎ ‎∵x≤32，‎ ‎∴当30≤x≤32时，w≥2000． ‎ 设成本为P（元），由题意，得：‎ ‎∵，‎ ‎∴P随x的增大而减小.‎ ‎∴当x = 32时，P最小＝3600.‎ 答：想要每月获得的利润不低于2000元，每月的成本最少为3600元．‎ ‎1．（2010年浙江省东阳市）阅读材料，寻找共同存在的规律：有一个运算程序a⊕b = n，‎ 可以使：（a+c）⊕b= n+c，a⊕（b+c）=n－2c，‎ 如果1⊕1=2，那么2010⊕2010 = ▲ ．‎ 关键词：阅读理解 答案：-2007 ‎ ‎1、（2010年宁波市）《几何原本》的诞生，标志着几何学已成为一个有着严密理论系统和科学方法的学科，它奠定了现代数学的基础，它是下列哪位数学家的著作（ ）‎ ‎ A、欧几里得 B、杨辉 C、费马 D、刘徽 ‎【关键词】数学阅读知识 ‎【答案】A ‎(2010年浙江省绍兴市)在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,‎ A y O B x 第21题图 叫做此一次函数的坐标三角形.例如，图中的一次函数的图象与 x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.‎ ‎（1）求函数y＝x＋3的坐标三角形的三条边长； ‎ ‎（2）若函数y＝x＋b（b为常数）的坐标三角形周长为16, 求此三角形面积.‎ ‎【答案】解：(1) ∵ 直线y＝x＋3与x轴的交点坐标为（4,0），与y轴交点坐标为（0,3）， ‎ ‎∴函数y＝x＋3的坐标三角形的三条边长分别为3,4,5. ‎ ‎(2) 直线y＝x＋b与x轴的交点坐标为（,0），与y轴交点坐标为（0,b）， ‎ 当b>0时,，得b =4，此时,坐标三角形面积为； ‎ 当b<0时，，得b =－4，此时,坐标三角形面积为. ‎ 综上,当函数y＝x＋b的坐标三角形周长为16时,面积为． ‎ ‎2010年益阳市） 我们把对称中心重合，四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等.‎ 一条直线l与方形环的边线有四个交点、、、．小明在探究线段与 的数量关系时，从点、向对边作垂线段、，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题：‎ ‎⑴当直线l与方形环的对边相交时（如图），直线l分别交、、、于、、、，小明发现与相等，请你帮他说明理由；‎ ‎⑵当直线l与方形环的邻边相交时（如图），l分别交、、、于、、‎ ‎、，l与的夹角为，你认为与还相等吗？若 相等，说明理由；若不相等，求出的值（用含的三角函数表示）.‎ ‎【关键词】正方形性质、相似三角形、三角函数值 ‎【答案】⑴解: 在方形环中，‎ ‎ ∵∥‎ ‎ ∴‎ ‎ ∴△≌△‎ ‎ ∴　　　　　　　　‎ ‎ ⑵解法一：∵‎ ‎　　　∴∽ ‎ ‎ ∴‎ ‎ ∵‎ ‎ ∴ （或）‎ ‎①当时，tan=1,则 ‎ ②当时，‎ ‎ 则 （或） 　　 ‎ 解法二：在方形环中，‎ ‎ 又∵‎ ‎ ∴∥‎ ‎ ∴‎ ‎ 在与中，‎ ‎ ‎ ‎ ‎ ‎ 即 （或）　　　‎ ‎ ①当时，‎ ‎ ②当时，‎ ‎ 则 （或） 　　　　　‎