2015临沂市中考数学试卷

2015临沂市中考数学试卷

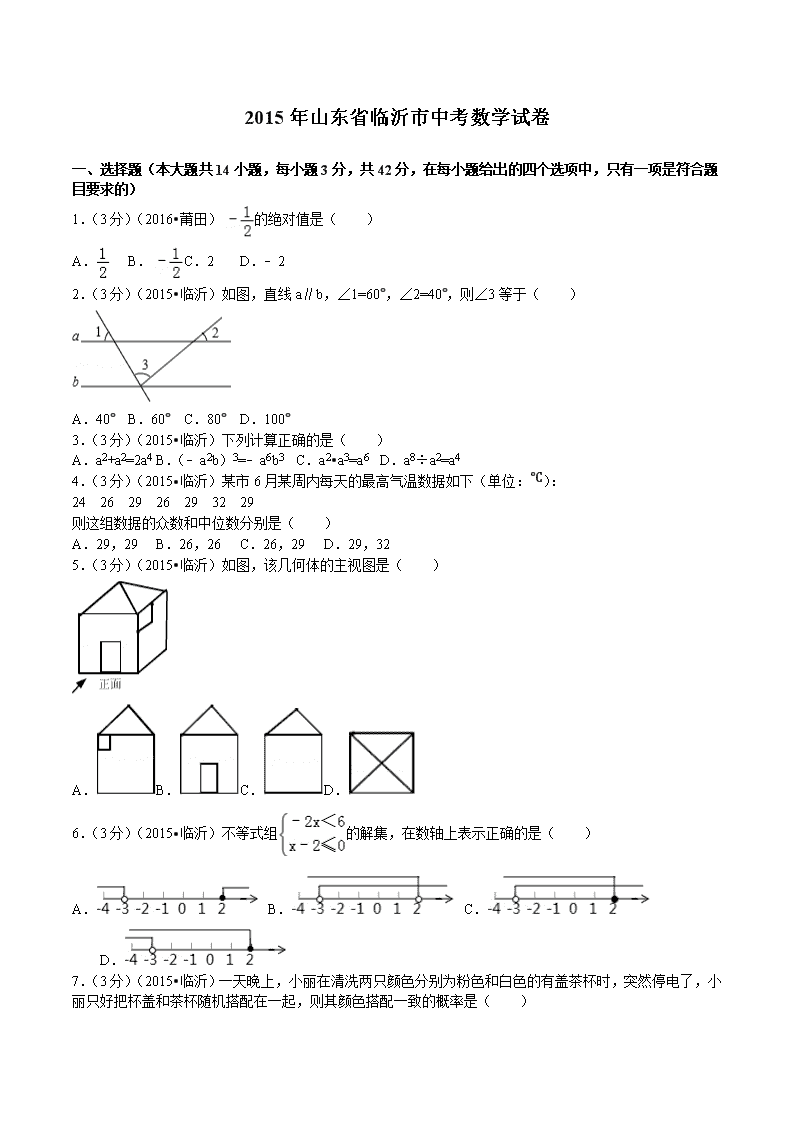
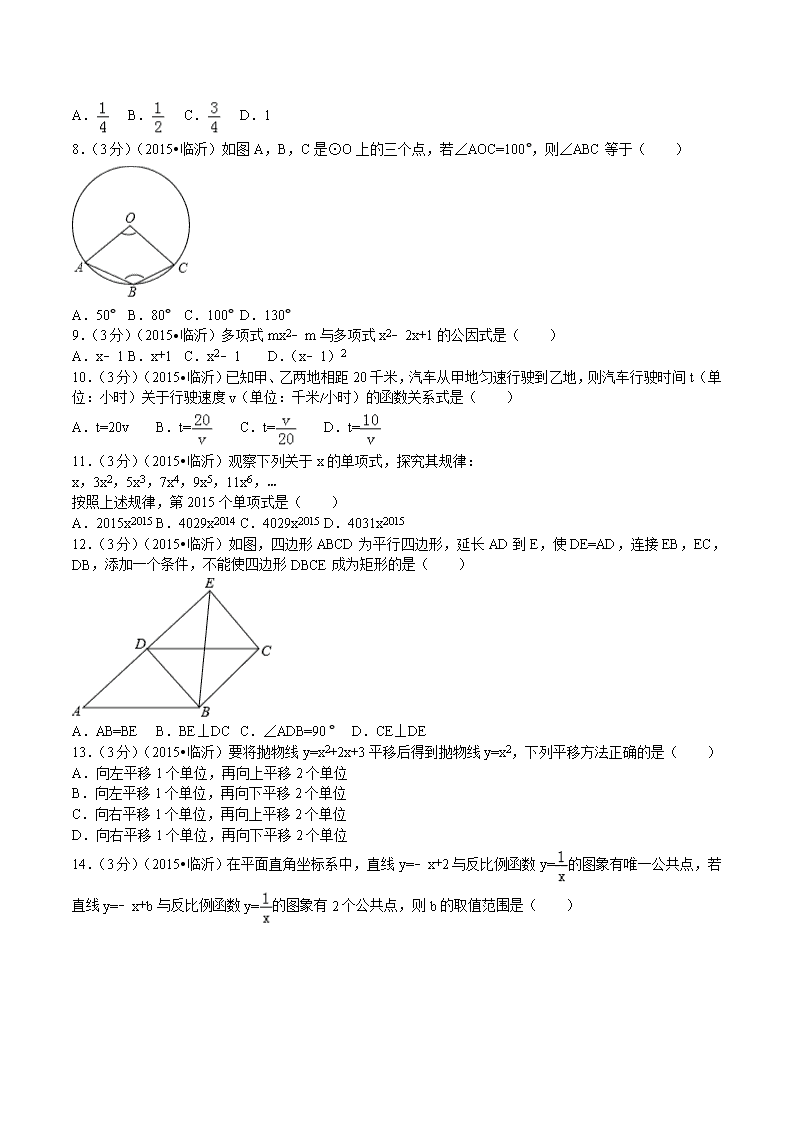
‎2015年山东省临沂市中考数学试卷 ‎　‎ 一、选择题（本大题共14小题，每小题3分，共42分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（3分）（2016•莆田）的绝对值是（　　）‎ A． B． C．2 D．﹣2‎ ‎2．（3分）（2015•临沂）如图，直线a∥b，∠1=60°，∠2=40°，则∠3等于（　　）‎ A．40° B．60° C．80° D．100°‎ ‎3．（3分）（2015•临沂）下列计算正确的是（　　）‎ A．a2+a2=2a4 B．（﹣a2b）3=﹣a6b3 C．a2•a3=a6 D．a8÷a2=a4‎ ‎4．（3分）（2015•临沂）某市6月某周内每天的最高气温数据如下（单位：℃）：‎ ‎24 26 29 26 29 32 29‎ 则这组数据的众数和中位数分别是（　　）‎ A．29，29 B．26，26 C．26，29 D．29，32‎ ‎5．（3分）（2015•临沂）如图，该几何体的主视图是（　　）‎ A． B． C． D．‎ ‎6．（3分）（2015•临沂）不等式组的解集，在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎7．（3分）（2015•临沂）一天晚上，小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时，突然停电了，小丽只好把杯盖和茶杯随机搭配在一起，则其颜色搭配一致的概率是（　　）‎ A． B． C． D．1‎ ‎8．（3分）（2015•临沂）如图A，B，C是⊙O上的三个点，若∠AOC=100°，则∠ABC等于（　　）‎ A．50° B．80° C．100° D．130°‎ ‎9．（3分）（2015•临沂）多项式mx2﹣m与多项式x2﹣2x+1的公因式是（　　）‎ A．x﹣1 B．x+1 C．x2﹣1 D．（x﹣1）2‎ ‎10．（3分）（2015•临沂）已知甲、乙两地相距20千米，汽车从甲地匀速行驶到乙地，则汽车行驶时间t（单位：小时）关于行驶速度v（单位：千米/小时）的函数关系式是（　　）‎ A．t=20v B．t= C．t= D．t=‎ ‎11．（3分）（2015•临沂）观察下列关于x的单项式，探究其规律：‎ x，3x2，5x3，7x4，9x5，11x6，…‎ 按照上述规律，第2015个单项式是（　　）‎ A．2015x2015 B．4029x2014 C．4029x2015 D．4031x2015‎ ‎12．（3分）（2015•临沂）如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（　　）‎ A．AB=BE B．BE⊥DC C．∠ADB=90° D．CE⊥DE ‎13．（3分）（2015•临沂）要将抛物线y=x2+2x+3平移后得到抛物线y=x2，下列平移方法正确的是（　　）‎ A．向左平移1个单位，再向上平移2个单位 B．向左平移1个单位，再向下平移2个单位 C．向右平移1个单位，再向上平移2个单位 D．向右平移1个单位，再向下平移2个单位 ‎14．（3分）（2015•临沂）在平面直角坐标系中，直线y=﹣x+2与反比例函数y=的图象有唯一公共点，若直线y=﹣x+b与反比例函数y=的图象有2个公共点，则b的取值范围是（　　）‎ A．b＞2 B．﹣2＜b＜2 C．b＞2或b＜﹣2 D．b＜﹣2‎ ‎　‎ 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎15．（3分）（2015•临沂）比较大小：2　　　　　　（填“＜”、“=”、“＞”）．‎ ‎16．（3分）（2015•临沂）计算：﹣=　　　　　　．‎ ‎17．（3分）（2015•临沂）如图，在▱ABCD中，连接BD，AD⊥BD，AB=4，sinA=，则▱ABCD的面积是　　　　　　．‎ ‎18．（3分）（2015•临沂）如图，在△ABC中，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O，则=　　　　　　．‎ ‎19．（3分）（2015•临沂）定义：给定关于x的函数y，对于该函数图象上任意两点（x1，y1），（x2，y2），当x1＜x2时，都有y1＜y2，称该函数为增函数，根据以上定义，可以判断下面所给的函数中，是增函数的有　　　　　　（填上所有正确答案的序号）‎ ‎①y=2x；②y=﹣x+1；③y=x2（x＞0）；④y=﹣．‎ ‎　‎ 三、解答题（本大题共7小题，共63分）‎ ‎20．（7分）（2015•临沂）计算：（+﹣1）（﹣+1）‎ ‎21．（7分）（2015•临沂）“保护环境，人人有责”，为了了解某市的空气质量情况，某校环保兴趣小组，随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．‎ 请你根据图中提供的信息，解答下列问题：‎ ‎（1）补全条形统计图；‎ ‎（2）估计该市这一年（365天）空气质量达到“优”和“良”的总天数；‎ ‎（3）计算随机选取这一年内某一天，空气质量是“优”的概率．‎ ‎22．（7分）（2015•临沂）小强从自己家的阳台上，看一栋楼顶部的仰角为30°，看这栋楼底部的俯角为60°，小强家与这栋楼的水平距离为42m，这栋楼有多高？‎ ‎23．（9分）（2015•临沂）如图，点O为Rt△ABC斜边AB上一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．‎ ‎（1）求证：AD平分∠BAC；‎ ‎（2）若∠BAC=60°，OA=2，求阴影部分的面积（结果保留π）．‎ ‎24．（9分）（2015•临沂）新农村社区改造中，有一部分楼盘要对外销售，某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2．‎ 若购买者一次性付清所有房款，开发商有两种优惠方案：‎ 方案一：降价8%，另外每套楼房赠送a元装修基金；‎ 方案二：降价10%，没有其他赠送．‎ ‎（1）请写出售价y（元/米2）与楼层x（1≤x≤23，x取整数）之间的函数关系式；‎ ‎（2）老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算．‎ ‎25．（11分）（2015•临沂）如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE．‎ ‎（1）请判断：AF与BE的数量关系是　　　　　　，位置关系是　　　　　　；‎ ‎（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予说明；‎ ‎（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．‎ ‎26．（13分）（2015•临沂）在平面直角坐标系中，O为原点，直线y=﹣2x﹣1与y轴交于点A，与直线y=﹣x交于点B，点B关于原点的对称点为点C．‎ ‎（1）求过A，B，C三点的抛物线的解析式；‎ ‎（2）P为抛物线上一点，它关于原点的对称点为Q．‎ ‎①当四边形PBQC为菱形时，求点P的坐标；‎ ‎②若点P的横坐标为t（﹣1＜t＜1），当t为何值时，四边形PBQC面积最大？并说明理由．‎ ‎　‎ ‎2015年山东省临沂市中考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（本大题共14小题，每小题3分，共42分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1．（3分）（2016•莆田）的绝对值是（　　）‎ A． B． C．2 D．﹣2‎ ‎【分析】根据负数的绝对值等于它的相反数解答．‎ ‎【解答】解：﹣的绝对值是．‎ 故选：A．‎ ‎　‎ ‎2．（3分）（2015•临沂）如图，直线a∥b，∠1=60°，∠2=40°，则∠3等于（　　）‎ A．40° B．60° C．80° D．100°‎ ‎【分析】根据对顶角相等和利用三角形的内角和定理列式计算即可得解．‎ ‎【解答】解：如图：‎ ‎∵∠4=∠2=40°，∠5=∠1=60°，‎ ‎∴∠3=180°﹣60°﹣40°=80°，‎ 故选C．‎ ‎　‎ ‎3．（3分）（2015•临沂）下列计算正确的是（　　）‎ A．a2+a2=2a4 B．（﹣a2b）3=﹣a6b3 C．a2•a3=a6 D．a8÷a2=a4‎ ‎【分析】根据同底数幂的乘除法、合并同类项以及积的乘方和幂的乘方进行计算即可．‎ ‎【解答】解：A、a2+a2=2a2B，故A错误；‎ B、（﹣a2b）3=﹣a6b3，故B正确；‎ C、a2•a3=a5，故C错误；‎ D、a8÷a2=a6，故D错误；‎ 故选B．‎ ‎　‎ ‎4．（3分）（2015•临沂）某市6月某周内每天的最高气温数据如下（单位：℃）：‎ ‎24 26 29 26 29 32 29‎ 则这组数据的众数和中位数分别是（　　）‎ A．29，29 B．26，26 C．26，29 D．29，32‎ ‎【分析】根据中位数和众数的定义求解：众数是一组数据中出现次数最多的数据，注意众数可以不止一个；找中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．‎ ‎【解答】解：将这组数据从小到大的顺序排列24，26，26，29，29，29，32，‎ 在这一组数据中29是出现次数最多的，故众数是29℃．‎ 处于中间位置的那个数是29，那么由中位数的定义可知，这组数据的中位数是29℃；‎ 故选A．‎ ‎　‎ ‎5．（3分）（2015•临沂）如图，该几何体的主视图是（　　）‎ A． B． C． D．‎ ‎【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中，从正面能看到门，不能看到窗户．‎ ‎【解答】解：从正面看易得是1个长方形（中间下面有一个小长方形）和一个三角形组成．‎ 故选B．‎ ‎　‎ ‎6．（3分）（2015•临沂）不等式组的解集，在数轴上表示正确的是（　　）‎ A． B． C． D．‎ ‎【分析】分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．‎ ‎【解答】解：，‎ 由①得，x＞﹣3，‎ 由②得，x≤2，‎ 故不等式组的解集为：﹣3＜x≤2．‎ 在数轴上表示为：‎ ‎．‎ 故选C．‎ ‎　‎ ‎7．（3分）（2015•临沂）一天晚上，小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时，突然停电了，小丽只好把杯盖和茶杯随机搭配在一起，则其颜色搭配一致的概率是（　　）‎ A． B． C． D．1‎ ‎【分析】根据概率的计算公式．颜色搭配总共有4种可能，分别列出搭配正确和搭配错误的可能，进而求出概率即可．‎ ‎【解答】解：用A和a分别表示粉色有盖茶杯的杯盖和茶杯；用B和b分别表示白色有盖茶杯的杯盖和茶杯、经过搭配所能产生的结果如下：Aa、Ab、Ba、Bb 所以颜色搭配正确的概率是；‎ 故选B．‎ ‎　‎ ‎8．（3分）（2015•临沂）如图A，B，C是⊙O上的三个点，若∠AOC=100°，则∠ABC等于（　　）‎ A．50° B．80° C．100° D．130°‎ ‎【分析】首先在上取点D，连接AD，CD，由圆周角定理即可求得∠D的度数，然后由圆的内接四边形的性质，求得∠ABC的度数．‎ ‎【解答】解：如图，在优弧上取点D，连接AD，CD，‎ ‎∵∠AOC=100°，‎ ‎∴∠ADC=∠AOC=50°，‎ ‎∴∠ABC=180°﹣∠ADC=130°．‎ 故选D．‎ ‎　‎ ‎9．（3分）（2015•临沂）多项式mx2﹣m与多项式x2﹣2x+1的公因式是（　　）‎ A．x﹣1 B．x+1 C．x2﹣1 D．（x﹣1）2‎ ‎【分析】分别将多项式mx2﹣m与多项式x2﹣2x+1进行因式分解，再寻找它们的公因式．‎ ‎【解答】解：mx2﹣m=m（x﹣1）（x+1），‎ x2﹣2x+1=（x﹣1）2，‎ 多项式mx2﹣m与多项式x2﹣2x+1的公因式是（x﹣1）．‎ 故选：A．‎ ‎　‎ ‎10．（3分）（2015•临沂）已知甲、乙两地相距20千米，汽车从甲地匀速行驶到乙地，则汽车行驶时间t（单位：小时）关于行驶速度v（单位：千米/小时）的函数关系式是（　　）‎ A．t=20v B．t= C．t= D．t=‎ ‎【分析】根据路程=时间×速度可得vt=20，再变形可得t=．‎ ‎【解答】解：由题意得：vt=20，‎ t=，‎ 故选：B．‎ ‎　‎ ‎11．（3分）（2015•临沂）观察下列关于x的单项式，探究其规律：‎ x，3x2，5x3，7x4，9x5，11x6，…‎ 按照上述规律，第2015个单项式是（　　）‎ A．2015x2015 B．4029x2014 C．4029x2015 D．4031x2015‎ ‎【分析】系数的规律：第n个对应的系数是2n﹣1．‎ 指数的规律：第n个对应的指数是n．‎ ‎【解答】解：根据分析的规律，得 第2015个单项式是4029x2015．‎ 故选：C．‎ ‎　‎ ‎12．（3分）（2015•临沂）如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（　　）‎ A．AB=BE B．BE⊥DC C．∠ADB=90° D．CE⊥DE ‎【分析】先证明四边形ABCD为平行四边形，再根据矩形的判定进行解答．‎ ‎【解答】解：∵四边形ABCD为平行四边形，‎ ‎∴AD∥BC，AD=BC，‎ 又∵AD=DE，‎ ‎∴DE∥BC，且DE=BC，‎ ‎∴四边形BCED为平行四边形，‎ A、∵AB=BE，DE=AD，∴BD⊥AE，∴▱DBCE为矩形，故本选项错误；‎ B、∵对角线互相垂直的平行四边形为菱形，不一定为矩形，故本选项正确；‎ C、∵∠ADB=90°，∴∠EDB=90°，∴▱DBCE为矩形，故本选项错误；‎ D、∵CE⊥DE，∴∠CED=90°，∴▱DBCE为矩形，故本选项错误．‎ 故选B．‎ ‎　‎ ‎13．（3分）（2015•临沂）要将抛物线y=x2+2x+3平移后得到抛物线y=x2，下列平移方法正确的是（　　）‎ A．向左平移1个单位，再向上平移2个单位 B．向左平移1个单位，再向下平移2个单位 C．向右平移1个单位，再向上平移2个单位 D．向右平移1个单位，再向下平移2个单位 ‎【分析】原抛物线顶点坐标为（﹣1，2），平移后抛物线顶点坐标为（0，0），由此确定平移规律．‎ ‎【解答】解：y=x2+2x+3=（x+1）2+2，该抛物线的顶点坐标是（﹣1，2），抛物线y=x2的顶点坐标是（0，0），‎ 则平移的方法可以是：将抛物线y=x2+2x+3向右移1个单位，再向下平移2个单位．‎ 故选：D．‎ ‎　‎ ‎14．（3分）（2015•临沂）在平面直角坐标系中，直线y=﹣x+2与反比例函数y=的图象有唯一公共点，若直线y=﹣x+b与反比例函数y=的图象有2个公共点，则b的取值范围是（　　）‎ A．b＞2 B．﹣2＜b＜2 C．b＞2或b＜﹣2 D．b＜﹣2‎ ‎【分析】联立两函数解析式消去y可得x2﹣bx+1=0，由直线y=﹣x+b与反比例函数y=的图象有2个公共点，得到方程x2﹣bx+1=0有两个不相等的实数根，根据根的判别式可得结果．‎ ‎【解答】解：解方程组得：x2﹣bx+1=0，‎ ‎∵直线y=﹣x+b与反比例函数y=的图象有2个公共点，‎ ‎∴方程x2﹣bx+1=0有两个不相等的实数根，‎ ‎∴△=b2﹣4＞0，‎ ‎∴b＞2，或b＜﹣2，‎ 故选C．‎ ‎　‎ 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎15．（3分）（2015•临沂）比较大小：2　＞　（填“＜”、“=”、“＞”）．‎ ‎【分析】利用的取值范围进而比较得出即可．‎ ‎【解答】解：∵1＜＜2，‎ ‎∴2＞．‎ 故答案为：＞．‎ ‎　‎ ‎16．（3分）（2015•临沂）计算：﹣=　　．‎ ‎【分析】为同分母，通分，再将分子因式分解，约分．‎ ‎【解答】解：=﹣==，‎ 故答案为：．‎ ‎　‎ ‎17．（3分）（2015•临沂）如图，在▱ABCD中，连接BD，AD⊥BD，AB=4，sinA=，则▱ABCD的面积是　3　．‎ ‎【分析】先由三角函数求出BD，再根据勾股定理求出AD，▱ABCD的面积=AD•BD，即可得出结果．‎ ‎【解答】解：∵AD⊥BD，‎ ‎∴∠ADB=90°，‎ ‎∵AB=4，sinA=，‎ ‎∴BD=AB•sinA==4×=3，‎ ‎∴AD===，‎ ‎∴▱ABCD的面积=AD•BD=3；‎ 故答案为：3．‎ ‎　‎ ‎18．（3分）（2015•临沂）如图，在△ABC中，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O，则=　2　．‎ ‎【分析】根据三角形的重心到顶点的距离等于到对边中点的距离的2倍列式进行计算即可求解．‎ ‎【解答】证明：∵△ABC的中线BD、CE相交于点O，‎ ‎∴点O是△ABC的重心，‎ ‎∴=2．‎ 故答案为：2．‎ ‎　‎ ‎19．（3分）（2015•临沂）定义：给定关于x的函数y，对于该函数图象上任意两点（x1，y1），（x2，y2），当x1＜x2时，都有y1＜y2，称该函数为增函数，根据以上定义，可以判断下面所给的函数中，是增函数的有　①③　（填上所有正确答案的序号）‎ ‎①y=2x；②y=﹣x+1；③y=x2（x＞0）；④y=﹣．‎ ‎【分析】根据一次函数、二次函数、反比例函数的性质进行分析即可得到答案．‎ ‎【解答】解：y=2x，2＞0，∴①是增函数；‎ y=﹣x+1，﹣1＜0，∴②不是增函数；‎ y=x2，当x＞0时，是增函数，∴③是增函数；‎ y=﹣，在每个象限是增函数，因为缺少条件，∴④不是增函数．‎ 故答案为：①③．‎ ‎　‎ 三、解答题（本大题共7小题，共63分）‎ ‎20．（7分）（2015•临沂）计算：（+﹣1）（﹣+1）‎ ‎【分析】先根据平方差公式展开得到原式=[+（﹣1）][﹣（﹣1）]=（）2﹣（﹣1）2，再根据完全平方公式展开后合并即可．‎ ‎【解答】解：原式=[+（﹣1）][﹣（﹣1）]‎ ‎=（）2﹣（﹣1）2=3﹣（2﹣2+1）‎ ‎=3﹣2+2﹣1‎ ‎=2．‎ ‎　‎ ‎21．（7分）（2015•临沂）“保护环境，人人有责”，为了了解某市的空气质量情况，某校环保兴趣小组，随机抽取了2014年内该市若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）．‎ 请你根据图中提供的信息，解答下列问题：‎ ‎（1）补全条形统计图；‎ ‎（2）估计该市这一年（365天）空气质量达到“优”和“良”的总天数；‎ ‎（3）计算随机选取这一年内某一天，空气质量是“优”的概率．‎ ‎【分析】（1）根据良的天数除以量所占的百分比，可得样本容量，根据样本容量乘以轻度污染所占的百分比，可得答案；‎ ‎（2）根据一年的时间乘以优良所占的百分比，可得答案；‎ ‎（3）根据根据一年中优的天数比上一年的天数，可得答案．‎ ‎【解答】解：（1）样本容量3÷5%=60，‎ ‎60﹣12﹣36﹣3﹣2﹣1=6，‎ 条形统计图如图：‎ ‎（2）这一年空气质量达到“优”和“良”的总天数为：‎ ‎365×=292；‎ ‎（3）随机选取这一年内某一天，空气质量是“优”的概率为：=．‎ ‎　‎ ‎22．（7分）（2015•临沂）小强从自己家的阳台上，看一栋楼顶部的仰角为30°，看这栋楼底部的俯角为60°，小强家与这栋楼的水平距离为42m，这栋楼有多高？‎ ‎【分析】求这栋楼的高度，即BC的长度，根据BC=BD+DC，在Rt△ABD和Rt△ACD中分别求出BD，CD即可．‎ ‎【解答】解：在Rt△ABD中，‎ ‎∵∠BDA=90°，∠BAD=30°，AD=42m，‎ ‎∴BD=ADtan30°=42×=14（m）．‎ 在Rt△ACD中，∠ADC=90°，∠CAD=60°，‎ ‎∴CD=ADtan60°=42×=42（m）．‎ ‎∴BC=BD+CD=14+42=56（m）．‎ 答：这栋楼的高度为56m．‎ ‎　‎ ‎23．（9分）（2015•临沂）如图，点O为Rt△ABC斜边AB上一点，以OA为半径的⊙O与BC切于点D，与AC交于点E，连接AD．‎ ‎（1）求证：AD平分∠BAC；‎ ‎（2）若∠BAC=60°，OA=2，求阴影部分的面积（结果保留π）．‎ ‎【分析】（1）由Rt△ABC中，∠C=90°，⊙O切BC于D，易证得AC∥OD，继而证得AD平分∠CAB．‎ ‎（2）如图，连接ED，根据（1）中AC∥OD和菱形的判定与性质得到四边形AEDO是菱形，则△AEM≌△DMO，则图中阴影部分的面积=扇形EOD的面积．‎ ‎【解答】（1）证明：∵⊙O切BC于D，‎ ‎∴OD⊥BC，‎ ‎∵AC⊥BC，‎ ‎∴AC∥OD，‎ ‎∴∠CAD=∠ADO，‎ ‎∵OA=OD，‎ ‎∴∠OAD=∠ADO，‎ ‎∴∠OAD=∠CAD，‎ 即AD平分∠CAB；‎ ‎（2）设EO与AD交于点M，连接ED．‎ ‎∵∠BAC=60°，OA=OE，‎ ‎∴△AEO是等边三角形，‎ ‎∴AE=OA，∠AOE=60°，‎ ‎∴AE=AO=OD，‎ 又由（1）知，AC∥OD即AE∥OD，‎ ‎∴四边形AEDO是菱形，则△AEM≌△DMO，∠EOD=60°，‎ ‎∴S△AEM=S△DMO，‎ ‎∴S阴影=S扇形EOD==．‎ ‎　‎ ‎24．（9分）（2015•临沂）新农村社区改造中，有一部分楼盘要对外销售，某楼盘共23层，销售价格如下：第八层楼房售价为4000元/米2，从第八层起每上升一层，每平方米的售价提高50元；反之，楼层每下降一层，每平方米的售价降低30元，已知该楼盘每套楼房面积均为120米2．‎ 若购买者一次性付清所有房款，开发商有两种优惠方案：‎ 方案一：降价8%，另外每套楼房赠送a元装修基金；‎ 方案二：降价10%，没有其他赠送．‎ ‎（1）请写出售价y（元/米2）与楼层x（1≤x≤23，x取整数）之间的函数关系式；‎ ‎（2）老王要购买第十六层的一套楼房，若他一次性付清购房款，请帮他计算哪种优惠方案更加合算．‎ ‎【分析】（1）根据题意分别求出当1≤x≤8时，每平方米的售价应为4000﹣（8﹣x）×30元，当9≤x≤23时，每平方米的售价应为4000+（x﹣8）×50元；‎ ‎（2）根据购买方案一、二求出实交房款的关系式，然后分情况讨论即可确定那种方案合算．‎ ‎【解答】解：（1）当1≤x≤8时，每平方米的售价应为：‎ y=4000﹣（8﹣x）×30=30x+3760 （元/平方米）‎ 当9≤x≤23时，每平方米的售价应为：‎ y=4000+（x﹣8）×50=50x+3600（元/平方米）．‎ ‎∴y=‎ ‎（2）第十六层楼房的每平方米的价格为：50×16+3600=4400（元/平方米），‎ 按照方案一所交房款为：W1=4400×120×（1﹣8%）﹣a=485760﹣a（元），‎ 按照方案二所交房款为：W2=4400×120×（1﹣10%）=475200（元），‎ 当W1＞W2时，即485760﹣a＞475200，‎ 解得：0＜a＜10560，‎ 当W1＜W2时，即485760﹣a＜475200，‎ 解得：a＞10560，‎ ‎∴当0＜a＜10560时，方案二合算；当a＞10560时，方案一合算．‎ ‎　‎ ‎25．（11分）（2015•临沂）如图1，在正方形ABCD的外侧，作两个等边三角形ADE和DCF，连接AF，BE．‎ ‎（1）请判断：AF与BE的数量关系是　相等　，位置关系是　互相垂直　；‎ ‎（2）如图2，若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF，且EA=ED=FD=FC”，第（1）问中的结论是否仍然成立？请作出判断并给予说明；‎ ‎（3）若三角形ADE和DCF为一般三角形，且AE=DF，ED=FC，第（1）问中的结论都能成立吗？请直接写出你的判断．‎ ‎【分析】（1）易证△ADE≌△DCF，即可证明AF与BE的数量关系是：AF=BE，位置关系是：AF⊥BE．‎ ‎（2）证明△ADE≌△DCF，然后证明△ABE≌△ADF即可证得BE=AF，然后根据三角形内角和定理证明∠AMB=90°，从而求证；‎ ‎（3）与（2）的解法完全相同．‎ ‎【解答】解：（1）AF与BE的数量关系是：AF=BE，位置关系是：AF⊥BE．‎ 答案是：相等，互相垂直；‎ ‎（2）结论仍然成立．‎ 理由是：∵正方形ABCD中，AB=AD=CD，‎ ‎∴在△ADE和△DCF中，，‎ ‎∴△ADE≌△DCF，‎ ‎∴∠DAE=∠CDF，‎ 又∵正方形ABCD中，∠BAD=∠ADC=90°，‎ ‎∴∠BAE=∠ADF，‎ ‎∴在△ABE和△ADF中，，‎ ‎∴△ABE≌△ADF，‎ ‎∴BE=AF，∠ABM=∠DAF，‎ 又∵∠DAF+∠BAM=90°，‎ ‎∴∠ABM+∠BAM=90°，‎ ‎∴在△ABM中，∠AMB=180°﹣（∠ABM+∠BAM）=90°，‎ ‎∴BE⊥AF；‎ ‎（3）第（1）问中的结论都能成立．‎ 理由是：∵正方形ABCD中，AB=AD=CD，‎ ‎∴在△ADE和△DCF中，，‎ ‎∴△ADE≌△DCF，‎ ‎∴∠DAE=∠CDF，‎ 又∵正方形ABCD中，∠BAD=∠ADC=90°，‎ ‎∴∠BAE=∠ADF，‎ ‎∴在△ABE和△ADF中，，‎ ‎∴△ABE≌△ADF，‎ ‎∴BE=AF，∠ABM=∠DAF，‎ 又∵∠DAF+∠BAM=90°，‎ ‎∴∠ABM+∠BAM=90°，‎ ‎∴在△ABM中，∠AMB=180°﹣（∠ABM+∠BAM）=90°，‎ ‎∴BE⊥AF．‎ ‎　‎ ‎26．（13分）（2015•临沂）在平面直角坐标系中，O为原点，直线y=﹣2x﹣1与y轴交于点A，与直线y=﹣x交于点B，点B关于原点的对称点为点C．‎ ‎（1）求过A，B，C三点的抛物线的解析式；‎ ‎（2）P为抛物线上一点，它关于原点的对称点为Q．‎ ‎①当四边形PBQC为菱形时，求点P的坐标；‎ ‎②若点P的横坐标为t（﹣1＜t＜1），当t为何值时，四边形PBQC面积最大？并说明理由．‎ ‎【分析】（1）联立两直线解析式可求得B点坐标，由关于原点对称可求得C点坐标，由直线y=﹣2x﹣1可求得A点坐标，再利用待定系数法可求得抛物线解析式；‎ ‎（2）①当四边形PBQC为菱形时，可知PQ⊥BC，则可求得直线PQ的解析式，联立抛物线解析式可求得P点坐标；②过P作PD⊥BC，垂足为D，作x轴的垂线，交直线BC于点E，由∠PED=∠AOC，可知当PE最大时，PD也最大，用t可表示出PE的长，可求得取最大值时的t的值．‎ ‎【解答】解：‎ ‎（1）联立两直线解析式可得，解得，‎ ‎∴B点坐标为（﹣1，1），‎ 又C点为B点关于原点的对称点，‎ ‎∴C点坐标为（1，﹣1），‎ ‎∵直线y=﹣2x﹣1与y轴交于点A，‎ ‎∴A点坐标为（0，﹣1），‎ 设抛物线解析式为y=ax2+bx+c，‎ 把A、B、C三点坐标代入可得，解得，‎ ‎∴抛物线解析式为y=x2﹣x﹣1；‎ ‎（2）①当四边形PBQC为菱形时，则PQ⊥BC，‎ ‎∵直线BC解析式为y=﹣x，‎ ‎∴直线PQ解析式为y=x，‎ 联立抛物线解析式可得，解得或，‎ ‎∴P点坐标为（1﹣，1﹣）或（1+，1+）；‎ ‎②当t=0时，四边形PBQC的面积最大．‎ 理由如下：‎ 如图，过P作PD⊥BC，垂足为D，作x轴的垂线，交直线BC于点E，‎ 则S四边形PBQC=2S△PBC=2×BC•PD=BC•PD，‎ ‎∵线段BC长固定不变，‎ ‎∴当PD最大时，四边形PBQC面积最大，‎ 又∠PED=∠AOC（固定不变），‎ ‎∴当PE最大时，PD也最大，‎ ‎∵P点在抛物线上，E点在直线BC上，‎ ‎∴P点坐标为（t，t2﹣t﹣1），E点坐标为（t，﹣t），‎ ‎∴PE=﹣t﹣（t2﹣t﹣1）=﹣t2+1，‎ ‎∴当t=0时，PE有最大值1，此时PD有最大值，即四边形PBQC的面积最大．‎ ‎　‎ 参与本试卷答题和审题的老师有：星期八；1987483819；张其铎；HJJ；HLing；ZJX；sjzx；2300680618；sd2011；CJX；dbz1018；王学峰；wkd；wdzyzmsy@126.com；1286697702；gsls；caicl；sdwdmahongye；zhjh；522286788（排名不分先后）‎ 菁优网 ‎2016年8月27日